UP Board Solutions for Class 6 Maths Chapter 7 ज्यामितीय अवधारणाएँ
UP Board Solutions for Class 6 Maths Chapter 7 ज्यामितीय अवधारणाएँ
अभ्यास 7(a)
प्रश्न 1.
निम्नलिखित शब्दों में से उपयुक्त शब्द चुनकर रिक्त स्थान की पूर्ति कीजिए (पूर्ति करके)- (असंख्य, एक, वक्र)
उत्तर-
(a) समतल में स्थित दो बिन्दुओं से होकर एक रेखा खींची जा सकती है।
(b) समतल में स्थित किसी रेखा में असंख्य बिन्दु होते हैं।
(c) गोले का तल वक्र होता है।
(d) समतल में स्थित एक बिन्दु से होकर असंख्य रेखाएँ खींची जा सकती हैं।
प्रश्न 2.
निम्नलिखित कथनों में सही कथन के सामने कोष्ठक में सही का चिह्न (✓) तथा गलत कथन के सामने क्रॉस का, चिहून (✗) लगाइए (चिडून लगाकर)-
उत्तर-
(a) कागज का तल समतल है। (✓)
(b) तीन असंरेखीय बिन्दुओं से असंख्य समतल खींचे जा सकते हैं। (✗)
(c) समतल में स्थित दो रेखाएँ सदैव समान्तुर होती हैं। (✗)
(a) कमरे की दीवार का तल समतल का एक उदाहरण है। (✓)
प्रश्न 3.
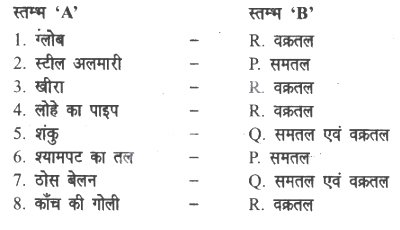
स्तम्भ ‘A’ एवं ‘B’ में सही जोड़े का मिलान कीजिए (सही मिलान करके)-
उत्तर-
प्रश्न 4.
ठोस बेलन में कितने समतल एवं वक्रतल होते हैं?
उत्तर-
ठोस बेलन में दो समतल एवं एक वक्रतल होता है।
प्रश्न 5.
समतल के तीन गुण बताइए।
उत्तर-
समतल के तीन गुण निम्नलिखित हैं-
- समतल में स्थित एक बिन्दु से असंख्य रेखाएँ खींची जा सकती हैं। ये सभी रेखाएँ कागज के तल पर स्थित होती हैं।
- समतल में स्थित दो बिन्दुओं से एक और केवल एक ही रेखा खीचीं जा सकती है। यह रेखा उसी तल में होती है जिसमें दोनों बिन्दु स्थित होते हैं।
- समतल में दो बिन्दुओं से जाने वाली रेखा का प्रत्येक बिन्दु तल पर स्थित होता है।
प्रश्न 6.
समतल वाली वस्तुओं एवं वक्रतल वाली वस्तुओं के चार-चार उदाहरण दीजिए।
उत्तर-
समतल वाली वस्तुएँ – मेज, दीवार, फर्श, सन्दूक।
वक्रतल वाली वस्तुएँ – फुटबॉल, तरबूज, कंचा, अण्डा।
अभ्यास 7(b)
प्रश्न 1.
अपनी अभ्यास पुस्तिका में एक रेखा खींचिए और अंग्रेजी वर्णमाला के एक छोटे अक्षर का प्रयोग करके उसका नाम लिखिए।
उत्तर-
![]()
प्रश्न 2.
अपने आस-पास में उपलब्ध वस्तुओं की सहायता से कोई तीन ऐसे उदाहरण दीजिए जिनसे रेखाओं (या उनके भाग) का बोध होता हो।
उत्तर-
- कमरे की दीवार,
- कमरे की छत,
- ब्लैक बोर्ड की भुजाएँ।
प्रश्न 3.
रेखा और किरण में अन्तर चित्र खींचकर स्पष्ट कीजिए।
उत्तर-
रेखा – रेखा को दोनों दिशाओं में विस्तार अपरिमित होता है। इसमें अन्त्य बिन्दु नहीं होता है।
![]()
किरण – किरण में केवल एक ही दिशा होती है तथा इसमें केवल एक ही अन्त्य बिन्दु होता है।
![]()
प्रश्न 4.
दिए गए प्रारम्भिक बिन्दु (निगमन बिन्दु) A और एक अन्य बिन्दु B से होकर जाती हुई एक किरण खींचिए।
उत्तर-
![]()
दक्षता अभ्यास – 7
प्रश्न 1.
तीन संरेख बिन्दुओं से होकर जाती हुई कितनी रेखाएँ खींची जा सकती हैं?
उत्तर-
तीन संरेख बिन्दुओं से होकर केवल एक रेखा खींची जा सकती है।
प्रश्न 2.
कागज के तल पर निम्नांकित बिन्दुओं को अंकित कर स्पष्ट कीजिए कि –
(a) एक बिन्दु से कितनी रेखाएँ खींची जा सकती हैं।
उत्तर-
एक बिन्दु से असंख्य रेखाएँ खींची जा सकती हैं।
(b) दो बिन्दुओं से कितनी रेखाएँ खींची जा सकती हैं।
उत्तर-
दो बिन्दुओं से एक रेखा खींची जा सकती है।
(c) तीन बिन्दु, जो संरेख नहीं हैं, में से दो-दो बिन्दुओं से कितनी रेखाएँ खींची जा सकती हैं।
उत्तर-
तीन रेखाएँ खींची जा सकती हैं।
(d) चार बिन्दु, जिनमें कोई तीन संरेख नहीं हैं, में से दो-दो बिन्दुओं से कितनी रेखाएँ खींची जा सकती हैं।
उत्तर-
छ: रेखाएँ खींची जा सकती हैं।
(e) पाँच बिन्दु, जिनमें कोई संरेख नहीं है, में से दो-दो बिन्दुओं से कितनी रेखाएँ खींची जा सकती हैं।
उत्तर-
दस रेखाएँ खींची जा सकती हैं।
प्रश्न 3.
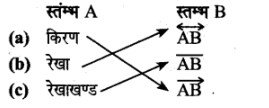
प्रश्न 4.
किसी तल पर स्थित एक रेखा में कितने बिन्दु हो सकते हैं?
उत्तर-
किसी तल पर स्थित एक रेखा में असंख्य बिन्दु हो सकते हैं।
प्रश्न 5.
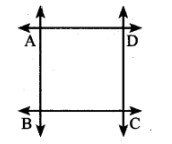
(i) दी गई आकृति में रेखाओं के नाम लिखिए।
उत्तर-
रेखा AB, रेखा BC, रेखा CD, तथा रेखा AD
(ii) आकृति की उन रेखाओं के नाम लिखिए जो बिन्दु A से होकर जाती हैं।
उत्तर-
रेखा AD तथा रेखा AB
प्रश्न 6.
निम्नांकित आकृति में एक बिन्दुगामी रेखाएँ और उनके संगमन बिन्दु लिखिए।
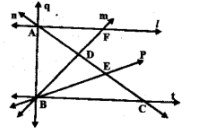
उत्तर-
(i) संगमन बिन्दु A तथा एक बिन्दुगामी रेखाएँ l, n, q
(ii) संगमन बिन्दु B तथा एक बिन्दुगामी रेखाएँ t, p, m, q
(iii) संगमन बिन्दु C तथा एक बिन्दुगामी रेखाएँ t, n
(iv) संगमन बिन्दु D तथा एक बिन्दुगामी रेखाएँ n, m
(v) संगमन बिन्दु E तथा एक बिन्दुगामी रेखाएँ n, p
(vi) संगमन बिन्दु F तथा एक बिन्दुगामी रेखाएँ m, l
प्रोजेक्ट :- नोट – विद्यार्थी स्वयं करें।
We hope the UP Board Solutions for Class 6 Maths Chapter 7 ज्यामितीय अवधारणाएँ help you.