UP Board Solutions for Class 12 Maths Chapter 12 Linear Programming

UP Board Solutions for Class 12 Maths Chapter 12 Linear Programming

UP Board Solutions for Class 12 Maths Chapter 12 Linear Programming

प्रश्नावली 12.1

ग्राफीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए
प्रश्न 1.
निम्न अवरोधों के अन्तर्गत Z = 3x + 4y का अधिकतमीकरण कीजिए।
x + y ≤ 4, x≥0, y≥0
हल-
दिये हुए असमीक़रणों को समीकरणों में बदलने पर,

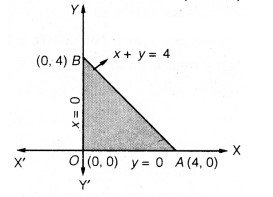
x + y = 4
x = 0, y = 0
अब हम उपरोक्त रेखाओं के आलेख खींचते हैं। संलग्न चित्र में सुसंगत क्षेत्र (छायांकित) OAB परिबद्ध है। सुसंगत क्षेत्र के कोनीय बिन्दु O(0,0), A(4,0), B(0, 4) हैं।
अब हम कोनीय बिन्दुओं पर उद्देशीय फलन Z का मान ज्ञात करते हैं।

अत: B(0, 4) पर Z अधिकतम है और अधिकतम मान 16 है।

प्रश्न 2.
निम्न अवरोधों के अन्तर्गत Z = -3x + 4y का न्यूनतमीकरण कीजिए
x + 2y≤8
3x + 2y≤12
x≥0, y≥0
हल-
सर्वप्रथम हम रेखाओं x + 2y = 8 …(i)
3x + 2y = 12 …(ii)
x = 0 …(iii)
y = 0 …(iv)

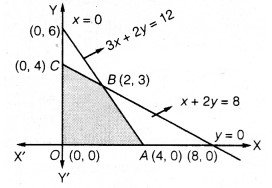
का आलेख खींचते हैं।
स्पष्ट है कि सुसंगत क्षेत्र (छायांकित) OABC परिबद्ध है। सुसंगत क्षेत्र के कोनीय बिन्दु O(0, 0), A (4, 0), B(2,3) और C(0, 4) हैं।
अब हम कोनीय बिन्दुओं पर उद्देशीय फलन Z का मान ज्ञात करते हैं।

अतः कोनीय बिन्दु A(4, 0) पर z का न्यूनतम मान = -12

प्रश्न 3.
निम्न अवरोधों के अन्तर्गत Z = 5x + 3y का अधिकतमीकरण कीजिए।
3x + 5y≤15;
5x + 2y≤10; x≥0, y≥0
हल-
सर्वप्रथम हम रेखओं
3x + 5y = 15 …(i)
5x + 2y = 10 …(ii)
x = 0, …(iii)
y = 0 …(iv)

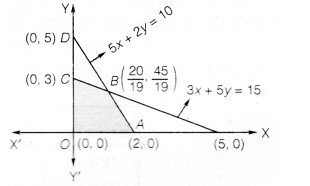
का आलेख खींचते हैं।
स्पष्ट है कि सुसंगत क्षेत्र (छायांकित) OABC परिबद्ध है।
सुसंगत क्षेत्र के कोनीय बिन्दु

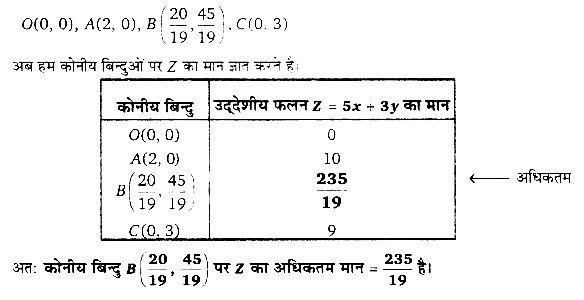
प्रश्न 4.
निम्न अवरोधों के अन्तर्गत Z = 3x + 5y का न्यूनतमीकरण कीजिए
x + 3y≥3; x + y≥2 x, y≥0
हल-
सर्वप्रथम हम रेखाओं
x + 3y = 3 …(i)
x + y = 2 …(ii)
x = 0 …(iii),
y = 0 ..(iv)
का आलेख खींचते हैं।

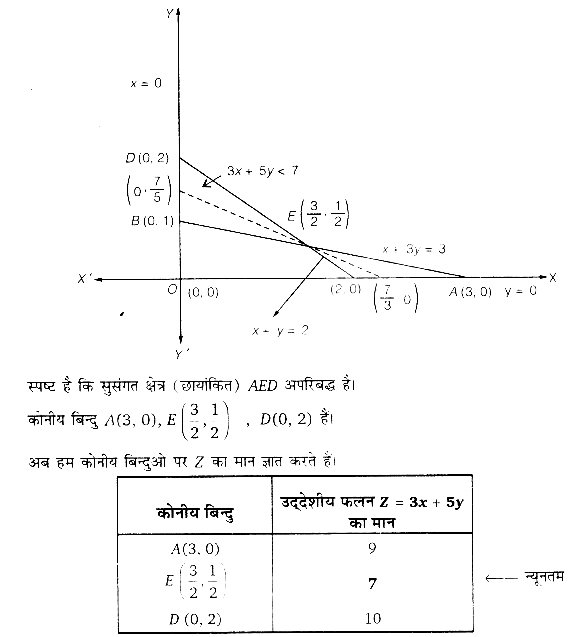
प्रश्न 5.
निम्न अवरोधों के अन्तर्गत Z = 3x + 2y का अधिकतमीकरण कीजिए
x + 2y≤10; 3x + y≤15; x, y≥0;
हल-
सर्वप्रथम निम्नलिखित रेखाओं
x + 2y = 10 …(i)
3x + y = 15 …(ii)
x = 0 …(iii)
y = 0 …(iv)
के आलेख खींचते हैं।
स्पष्ट है कि सुसंगत क्षेत्र OABC (छायांकित) परिबद्ध है।
जिसके कोनीय बिन्दु O(0, 0), A(5,0), B(4, 3), C(0, 5) हैं।
अब हम कोनीय बिन्दुओं पर Z का मान ज्ञात करते हैं।


Z का अधिकतम मान कोनीय बिन्दु B (4, 3) पर है जोकि 18 है।

प्रश्न 6.
निम्न अवरोधों के अन्तर्गत Z = x + 2y का न्यूनतमीकरण कीजिए
2x + y≥3; x + 2y≥6; x, y≥0
दिखाइए कि z का न्यूनतम मान दो बिन्दुओं से अधिक बिन्दुओं पर घटित होता है।
हल-
सर्वप्रथम निम्नलिखित रेखाओं
2x + y = 3 …(i)
x + 2y = 6 …(ii)
x = 0, …(iii)
y = 0 …(iv)
के आलेख खींचते हैं।

स्पष्ट है कि सुसंगत क्षेत्र (छायांकित) अपरिबद्ध है।
जिसके कोनीय बिन्दु A(6, 0), B(0, 3) हैं।
अब हम कोनीय बिन्दुओं पर Z का मान ज्ञात करते हैं।

∴ बिन्दु A व B दोनों पर Z का न्यूनतम मान 6 है। अतः A व B को मिलाने वाली रेखा के प्रत्येक बिन्दु पर Z का मान न्यूनतम होगा।

प्रश्न 7.
निम्नलिखित अवरोधों के अन्तर्गत Z = 5x + 10y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए
x + 2x≤120; x + y≥60; x – 2y≥0, x, y≥0
हल-
सर्वप्रथम हम निम्नलिखित रेखाओं
x + 2y = 120 …(i)
x + y = 60 …(ii)
x – 2y = 0 …(iii)
x = 0 …(iv)
y = 0 …(v)

के आलेख खींचते हैं। स्पष्ट है कि सुसंगत क्षेत्र (छायांकित) ADEC परिबद्ध है।
जिसके कोनीय बिन्दु हैं A (120, 0), D(60, 30), E(20, 40), C (60, 0)
कोनीय बिन्दुओं पर उद्देशीय फलन Z का मान ज्ञात करते हैं।

अत: C (60, 0) पर Z का न्यूनतम मान 300 है और A(120, 0) और D(60, 30) पर Z का अधिकतम मान 600 है अर्थात् AD के प्रत्येक बिन्दु पर Z का अधिकतम मान 600 है।

प्रश्न 8.
निम्न अवरोधों के अन्तर्गत Z = x + 2y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए
x + 2y≥100; 2x – y≤0; 2x + y≤200; x, y≥0
हल-
सर्वप्रथम हम रेखाओं
x + 2y = 100 …(i)
2x – y = 0 …(ii)
2x + y = 200 …(iii)
x = 0, …(iv)
y = 0 …(v)
के आलेख खींचते हैं।
स्पष्ट है कि सुसंगत क्षेत्र (छायांकित) BCDE है जोकि परिबद्ध है।
जिसके कोनीय बिन्दु B(0, 50), C(0, 200), D(50, 100) और E(20, 40) हैं।
अब हम कोनीय बिन्दुओं पर Z का मान ज्ञात करते हैं

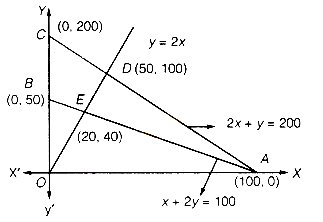
अतः बिन्दु (0, 200) पर अधिकतम मान 400 है।
तथा बिन्दु B 0, 50) व E (20,40) पर Z का न्यूनतम मान 100 है।
अर्थात् (0, 50) और (20,40) को मिलाने वाले रेखाखण्ड के प्रत्येक बिन्दु पर Z का न्यूनतम मान 100 है।

प्रश्न 9.
निम्न अवरोधों के अन्तर्गत Z = -x + 2y का अधिकतमीकरण कीजिए
x≥3; x + y≥5;
x + 2y≥6; y≥0
हल-
सर्वप्रथम हम रेखाओं
x = 3 …(i)
x + y = 5 …(ii)
x + 2y = 6 …(iii)
y = 0 …(iv)

के आलेख खींचते हैं।
स्पष्ट है कि सुसंगत क्षेत्र (छायांकित) अपरिबद्ध है। जिसके कोनीय बिन्दु A (6,0), B (4, 1) और C(3, 2) हैं।
अब हम कोनीय बिन्दु पर Z का मान ज्ञात करते हैं।

सारणी से स्पष्ट है कि Z का अधिकतम मान बिन्दु (3, 2) पर है। परन्तु चूंकि क्षेत्र अपरिबद्ध है अतः z का यह मान अधिकतम हो सकता हैं और नहीं भी।
यह ज्ञात करने के लिए असमिका -x + 2y >1…(v) का आलेख खींचते हैं। आलेख द्वारा प्राप्त खुले अर्द्धतल व सुसंगत क्षेत्र में उभयनिष्ठ बिन्दु हैं। अतः Z का कोई अधिकतम मान सम्भव नहीं है।

प्रश्न 10.
निम्न अवरोधों के अन्तर्गत Z = x + y का अधिकतमीकरण कीजिए।
x – y≤ -1; – x + y≤0; x, y≥0
हल-
सर्वप्रथम हम निम्नलिखित रेखाओं
x – y = 1 …(i)
-x + y = 0 …(ii)
x = 0…(iii),
y = 0 …(iv)

के आलेख खींचते हैं।
संलग्न चित्र से हम देखते हैं कि ऐसा कोई बिन्दु नहीं है जो । सभी अवरोधों को एक साथ सन्तुष्ट करे। अत: इस समस्या का कोई सुसंगत हल नहीं है।

प्रश्नावली 12.2

प्रश्न 1.
रश्मि दो प्रकार के भोज्य P और Q को इस प्रकार मिलाना चाहती है कि मिश्रण में विटामिन अवयवों में 8 मात्रक विटामिन A तथा 11 मात्रक विटामिन B हों। भोज्य P की लागत Rs 60/किग्रा और भोज्य Q की लागत Rs 80 किग्रा है। भोज्य P में 3 मात्रक/किग्रा विटामिन A और 5 मात्रक/kg विटामिन B है जबकि भोज्य Q में 4 मात्रक/किग्रा विटामिन A और 2 मात्रक/किग्रा विटामिन B है। मिश्रण की न्यूनतम लागत ज्ञात कीजिए।
हल-
माना मिश्रण में x किग्रा भोज्य P का और y किग्रा भोज्य B का है।
हम प्रदत्त आँकड़ों से निम्न सारणी बनाते हैं।

क्योंकि विटामिन A की न्यूनतम आवश्यकता 8 मात्रक है।
3x + 4y≥8
इसी प्रकार, विटामिन B की आवश्यकता 11 मात्रक है।
5x + 2y≥11
जबकि
x≥20, y≥0
1 किग्रा भोज्य P का क्रय मूल्य = Rs 60
1 किग्रा भोज्य Q का क्रय मूल्य = Rs 80
x किग्रा भोज्य P और y किग्रा भोज्य Q की कुल लागत Z = 60x + 80y
अतः समस्या को गणितीय रूप में निम्नलिखित रूप से व्यक्त किया सकता हैनिम्न व्यवरोधों के अन्तर्गत 3x + 42≥8 …..(i)
5x + 2y≥11 …..(ii)
x ≥ 0, y ≥ 0 …..(iii)
Z = 60x + 80y का न्यूनतमीकरण कीजिए।

प्रश्न 2.
एक प्रकार के केक को 200 ग्राम आटा तथा 25 ग्राम वसा (Fat) की आवश्यकता होती है। तथा दूसरी प्रकार के केक के लिए 100 ग्राम आटा तथा 50 ग्राम वसा की आवश्यकता होती है। केकों की अधिकतम संख्या बताओं जो 5 किलो आटे तथा 1 किलो वसा से बना सकते हैं, यह मान लिया गया है कि केकों को बनाने के लिए अन्य पदार्थों की कमी नहीं रहेगी।
हल-
माना पहली प्रकार के केक x हैं और दूसरी प्रकार के केक y हैं।
दिये गये आँकड़ों से निम्न सारणी बनाते हैं

दी गई शर्तों के अनुसार, समस्या को इस प्रकार लिख सकते हैं
व्यवरोधों 200x + 100y ≤ 5000
अर्थात् 2x + y ≤ 50 …(i)
और 25x + 50y ≤ 1000
अर्थात् x + 2y ≤ 40 …(ii)
तथा x ≥ 0 …(iii) y ≥ 0 …(iv)
के अन्तर्गत Z = x + y का अधिकतम मान ज्ञात कीजिए।
उपरोक्त असमिकाओं की संगत समीकरणों की रेखाओं के आलेख खींचते हैं। चित्र से स्पष्ट है कि सुसंगत क्षेत्र OABC (परिबद्ध) है। जिसके कोनीय बिन्दु O(0, 0), A(25,0), B(20, 10) और C(0, 20) हैं।

अब हम कोनीय बिन्दुओं पर Z का मान ज्ञात करते हैं

चूंकि B(20, 10) पर Z अधिकतम है अर्थात् 20 केक एक प्रकार के और 10 केक दूसरी प्रकार के बनाने होंगे, केकों की अधिकतम संख्या = 30 है।

प्रश्न 3.
एक कारखाने में टेनिस के रैकेट तथा क्रिकेट के बल्ले बनते हैं। एक टेनिस रैकेट बनाने के लिए 1.5 घण्टा यांत्रिक समय तथा 3 घण्टे शिल्पकार का समय लगता है। एक किक्रेट बल्ले को तैयार करने में 3 घण्टे यांत्रिक समय तथा 1 घण्टा शिल्पकार का समय लगता है। एक दिन में कारखाने में विभिन्न यंत्रों पर उपलब्ध यांत्रिक समय के 42 घण्टे और शिल्पकार समय के 24 घण्टे से अधिक नहीं हैं।
(i) रैकेटों और बल्लों को कितनी संख्या में बनाया जाए ताकि कारखाना पूरी क्षमता से कार्य करें?
(ii) यदि रैकेट और बल्ले पर लाभ क्रमशः ३ 20 तथा १ 10 हों, तो कारखाने का अधिकतम लाभ ज्ञात कीजिए यदि कारखाना पूरी क्षमता से कार्य करे।
हल-
(i) माना रैकेट बनाने की संख्या = x और बल्ले बनाने की संख्या = y
दिये गये आँकड़ों से निम्न सारणी बनाते हैं

इसलिए हम इस रैखिक प्रोग्रामन समस्या को इस प्रकार लिख सकते हैं
Z = x + y का अधिकतम मान निकालें।
जबकि 1.5x + 3y ≤ 42
अर्थात् x + 2y ≤ 28 …(i)
3x + y ≤ 24 …(ii)
x ≥ 0 …(iii)
y ≥ 0 …(iv)
उपरोक्त असमिकाओं के संगत समीकरणों में बदलकर आलेख खींचते हैं।

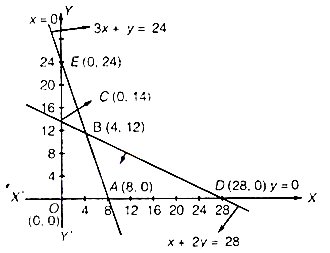
चित्र से स्पष्ट है कि सुसंगत क्षेत्र OABC (छायांकित) परिबद्ध है। जिसके कोनीय बिन्दु O(0, 0), A(8, 0), B(4, 12), C(0, 14) हैं।
अब हम कोनीय बिन्दुओं पर Z का मान ज्ञात करते हैं

चूंकि B(4, 12) पर Z अधिकतम है।
इसलिए रैकेट की संख्या = 4; बल्लों की संख्या = 12
(ii) लाभ फलन P = 20x + 10y; लाभ अधिकतम है जब x = 4, y = 12
अधिकतम लाभ = 20 x 4 + 10 x 12 = 80 + 120 = Rs 200

प्रश्न 4.
एक निर्माणकर्ता नट और बोल्ट का निर्माण करता है। एक पैकेट नटों में निर्माण में मशीन A पर एक घण्टा और मशीन B पर 3 घण्टे काम करना पड़ता है, जबकि एक पैकेट बोल्ट के निर्माण में 3 घण्टे मशीन A पर और 1 घण्टा मशीन B पर काम करना पड़ता है। वह नटों से Rs 17.50 प्रति पैकेट और बोल्टों पर Rs 7.00 प्रति पैकेट लाभ कमाता है। यदि प्रतिदिन मशीनों का अधिकतम उपयोग 12 घण्टे किया जाए तो प्रत्येक (नट और बोल्ट) के कितने पैकेट उत्पादित किए जाएँ ताकि अधिकतम लाभ कमाया जा सके।
हल-
माना निर्माणकर्ता नट के x पैकेट तथा बोल्ट के y पैकेटों का निर्माण करता है।
तो निर्माणकर्ता को लाभ Z = Rs (17.5x + 7y)
अतः स्पष्ट है कि x≥0, y≥0
अब दिये गये आँकड़ों से निम्न सारणी बनाते हैं।

अत: निम्न व्यवरोध प्राप्त होते हैं।
x + 3y ≤ 12 मशीन A के लिए
3x + y ≤ 12 मशीन B के लिए
अत: गणितीय समस्या का सूत्रीकरण निम्नलिखित है
Z = Rs (17.5x + 7y) का अधिकतमीकरण कीजिए जबकि निम्नलिखित व्यवरोध हैं।
x + 3y ≤ 12 …(i)
3x + y ≤ 12 …(ii)
x ≥ 0,y ≥ 0 …(iii)
असमिकाओं (i) से (iii) तक के आलेखों द्वारा निर्धारित सुसंगत क्षेत्र चित्र में दर्शाया गया है।

स्पष्ट है कि सुसंगत क्षेत्र परिबद्ध है।
अब हम कोनीय बिन्दुओं (0, 0), (4,0), (3, 3) और (0, 4) पर Z का मान ज्ञात करते हैं।

उपर्युक्त सारणी से स्पष्ट है कि बिन्दु (3, 3) पर Z का मान अधिकतम Rs 73.5 है।
अतः निर्माणकर्ता को 3 बोल्ट के पैकेट व 3 नटों के पैकेटों का निर्माण करना चाहिए ताकि अधिकतम लाभ Rs 73.5 हो।

प्रश्न 5.
एक कारखाने में दो प्रकार के पेंच A और B बनते हैं। प्रत्येक के निर्माण में दो मशीनों के प्रयोग की आवश्यकता होती है, जिसमें एक स्वचालित और दूसरी हस्तचालित है। एक पैकेट पेंच के निर्माण में 4 मिनट स्वचालित और 6 मिनट हस्तचालित मशीन, तथा एक पैकेट पेंच B के निर्माण में 6 मिनट स्वचालित और 3 मिनट हस्तचालित मशीन का कार्य होता है। प्रत्येक मशीन किसी भी दिन के लिए अधिकतम 4 घण्टे काम के लिए उपलब्ध है। निर्माता पेंच A के प्रत्येक पैकेट पर 37 और पेंच B के प्रत्येक पैकेट पर Rs 10 का लाभ कमाता है। यह मानते हुए कि कारखाने में निर्मित सभी पेंचों के पैकेट बिक जाते हैं, ज्ञात कीजिए कि प्रतिदिन कितने पैकेट विभिन्न पेंचों के बनाए जाएँ जिससे लाभ अधिकतम हो तथा अधिकतम लाभ ज्ञात कीजिए।
हल-
माना पेंच A की संख्या = x और पेंच B की संख्या = y
तब प्रदत्त आँकड़ों से निम्नलिखित सारणी बनाते हैं

अतः दी गई समस्या का गणितीय निरूपण इस प्रकार है
Z = 7x+10y का अधिकतम मान ज्ञात कीजिए। जबकि
4x + 6y ≤ 240 ⇒ 2x + 3y ≤ 120 …(i)
6x +3y ≤ 240 ⇒ 2x + y ≤ 80 …(ii)
x ≥ 0 …(iii), y ≥ 0 …(iv)
उपरोक्त असमिकाओं के संगत समिकाओं के आलेख खींचते हैं।
चित्र से स्पष्ट है कि सुसंगत क्षेत्र OABCD (छायाँकित) परिबद्ध है।

कोनीय बिन्दु हैं o(0, 0), A(40, 0), B (30, 20), C(0, 40)
अब कोनीय बिन्दुओं पर Z का मान ज्ञात करते हैं

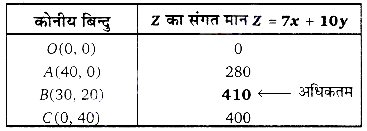
अत: B(30, 20) पर लाभ अधिकतम है।
∴ पेंच A की संख्या = 30 और पेंच B की संख्या = 20
और अधिकतम लाभ = Rs 410

प्रश्न 6.
एक निर्माता कम्पनी पैडेस्टल लैंप और लकड़ी के शेड बनाती है। प्रत्येक के निर्माण में एक रगड़ने/काटने और एक स्प्रेयर की आवश्यकता पड़ती है। एक लैंप के निर्माण में 2 घण्टे रगड़ने/काटने और 3 घण्टे स्प्रेयर की आवश्यकता होती है, जबकि एक शेड के निर्माण में 1 घण्टा रगड़ने/काटने और 2 घण्टे स्प्रेयर की आवश्यकता होती है। स्प्रेयर की मशीन प्रतिदिन अधिकतम 20 घण्टे और रगड़ने/काटने की मशीन प्रतिदिन अधिकतम 12 घण्टे के लिए उपलब्ध है। एक लैंप की बिक्री पर Rs 5 और एक शेड की बिक्री पर Rs 3 का लाभ होता है। यह मानते हुए कि सभी निर्मित लैंप और शेड बिक जाते हैं, तो बताइए वह निर्माण की प्रतिदिन कैसी योजना बनाए कि लाभ अधिकतम हो?
हल-
माना पैडेस्टेल लैंप की संख्या = x और लकड़ी के शेड की संख्या = y
दिये गये आँकड़ों से निम्न सारणी बनाते हैं

दी गई रैखिक प्रोग्रामन समस्या का गणितीय निरूपण इस प्रकार है–
Z = 5 + 3y का अधिकतम मान निकालिए—
जबकि 2x + y ≤ 12 …(i)
3x + 2y ≤ 20 …(ii)
x ≥ 0 …(iii)
y ≥ 0 …(iv)

उपरोक्त असमिकाओं के संगत समिकाओं का आलेख खींचते हैं। चित्र से स्पष्ट है कि संगत क्षेत्र OABC , (छायांकित)परिबद्ध है जिसके कोनीय बिन्दु O(0, 0), A(6, 0),B(4, 4), C(10, 10) हैं।
अब हम इन कोनीय बिन्दुओं पर Z का मान ज्ञात करते हैं

अत: B(4, 4) पर Z = 32 अधिकतम है।
इसलिए पैडेस्टेल लैंप की संख्या = 4, लकड़ी के शेड की संख्या = 4

प्रश्न 7.
एक कम्पनी प्लाईवुड के अनूठे स्मृति चिह्न का निर्माण करती है। A प्रकार के प्रति स्मृति चिह्न के निर्माण में 5 मिनट काटने और 10 मिनट जोड़ने में लगते हैं। B प्रकार के प्रति स्मृति चिह्न के लिए 8 मिनट काटने और 8 मिनट जोड़ने में लगते हैं। दिया गया है कि काटने के कुल समय 3 घण्टे 20 मिनट तथा जोड़ने के लिए 4 घण्टे उपलब्ध हैं। प्रत्येक A प्रकार के स्मृति चिह्न पर Rs 5 और प्रत्येक B प्रकार के स्मृति चिह्न पर Rs 6 का लाभ होना है। ज्ञात कीजिए कि लाभ के अधिकतमीकरण के लिए प्रत्येक प्रकार के कितने-कितने स्मृति चिह्नों का कम्पनी द्वारा निर्माण होना चाहिए?
हल-
माना A प्रकार के स्मृति चिह्न = x और B प्रकार के स्मृति चिह्न = y
दिये गये आँकड़ों से निम्नलिखित सारणी बनाते हैं

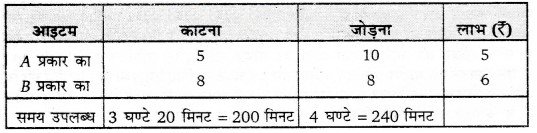
अतः उपरोक्त रैखिक प्रोग्रामन समस्या का गणितीय निरूपण इस प्रकार होगा–
Z = 5x + 6y का अधिकतम मान निकालिए।
जबकि 5x + 8y ≤ 200 …(i)
10x + 8y ≤ 240
5x + 43 ≤ 120 …(ii)
x ≥ 0 …(iii), y ≥ 0 …(iv)
उपरोक्त असमिकाओं के संगत समिकाओं के आलेख खींचते हैं।

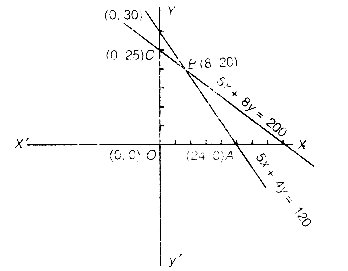
चित्र से स्पष्ट है कि सुसंगत क्षेत्र (छायांकित) OABC परिबद्ध है।
कोनीय बिन्दु O(0, 0), A(24, 0), B(8, 20), C(0, 25) हैं।
इन कोनीय बिन्दुओं पर Z का मान ज्ञात करते हैं—

अत: Z का अधिकतम मान 160 बिन्दु B(8, 20) पर है।
∴अधिकतम लाभ के लिए टाइप 3 के स्मृति चिह्न = 8 और B टाइप के = 20

प्रश्न 8.
एक सौदागर दो प्रकार के निजी कम्प्यूटर एक डेस्कटॉप नमूना और दूसरा पोर्टेबल नमूना, जिनकी कीमतें क्रमशः Rs 25000 और Rs 40000 होगी, बेचने की योजना बनाता है। वह अनुमान लगाता है कि कम्प्यूटरों की कुल मासिक माँग 250 नगों से अधिक नहीं होगी। प्रत्येक प्रकार के कम्प्यूटरों के नगों की संख्या ज्ञात कीजिए जिसे सौदागर अधिकतम लाभ प्राप्त करने के लिए संग्रह करें यदि उसके पास निवेश के लिए 70 लाख से अधिक नहीं है और डेस्कटॉप नमूने पर उसका लाभ Rs 4500 और पोर्टेबल नमूने पर Rs 5000 लाभ हो।
हल-
माना डेस्कटॉप नमूना कम्प्यूटर की संख्या = x
और पोर्टेबल नमूना कम्प्यूटर की संख्या = y
एक कम्प्यूटर पर लागत और लाभ निम्नलिखित है

अतः उपरोक्त रैखिक प्रोग्रामन समस्या का गणितीय निरूपण इस प्रकार होगा—
Z = 4500x + 5000y का अधिकतम मान निकालिए।
जबकि x + y ≤250 …(i)
25000x + 40000y ≤7000000
5x + 8y ≤ 1400 …(ii)
x > 0 …(iii)
y > 0 …(iv)
उपरोक्त असमिकाओं के संगत समिकाओं के आलेख खींचते हैं।

स्पष्ट है कि सुसंगत क्षेत्र (छायांकित) OABC परिबद्ध है।
जिसके कोनीय बिन्दु O(0, 0), A(250, 0), B(200, 50), C(0, 175) हैं।
अब हम Z का इन कोनीय बिन्दुओं पर मान ज्ञात करते हैं

अत: B(200, 50) पर Z अधिकतम है, इसलिए अधिकतम लाभ के लिए डेस्कटॉप कम्प्यूटर 200 और पोर्टेबल कम्प्यूटर 50 होंगे।

प्रश्न 9.
एक भोज्य पदार्थ में कम से कम 80 मात्रक विटामिन A और 100 मात्रक खनिज होना चाहिए। दो प्रकार के भोज्य F1 और F2 उपलब्ध हैं। भोज्य F1 की लागत Rs 4 प्रति मात्रक और F2 की लागत Rs 6 प्रति मात्रक है। भोज्य F1 की एक इकाई में कम-से-कम 3 मात्रक विटामिन A और 4 मात्रक खनिज हैं। F2 की प्रति इकाई में कम-से-कम 6 मात्रक विटामिन A और 3 मात्रक खनिज हैं। इसको एक रैखिक प्रोग्रामन समस्या के रूप में सूत्रबद्ध कीजिए। उस आहार का न्यूनतम मूल्य ज्ञात कीजिए जिसमें इन दो भोज्यों का मिश्रण है और उसमें न्यूनतम पोषक तत्त्व है।
हल-
माना भोज्य पदार्थ में भोज्य F1 की x इकाई तथा भोज्य F2 की y इकाई का मिश्रण होता है।
तब रैखिक प्रोग्रामन समस्या का गणितीय रूप होगा
Z = 4x + 6y (लागत फलन)
जबकि 3x +6y ≥ 80 (विटामिन A व्यवरोध)
4x + 3y ≥ 100 (विटामिन B व्यवरोध)
x, y ≥ 0 (ऋणेत्तर व्यवरोध)
उपरोक्त असमिकाओं के संगत समिकाओं के आलेख खींचते हैं

हम 4x + 6y < 104 अर्थात् 2x + 3y < 52 का आलेख खींचते हैं।
हम देखते हैं कि 2x + 3y < 52 द्वारा निरूपित खुले अर्द्धतल और सुसंगत क्षेत्र का कोई उभयनिष्ठ हल नहीं है।
अतः Z का न्यूनतम मान 104 है।

प्रश्न 10.
दो प्रकार के उर्वरक F1 अं F2 हैं। F1 में 10% नाइट्रोजन तथा 6% फॉस्फोरिक अम्ल है तथा F2 में 5% नाइट्रोजन तथा 10% फॉस्फोरिक अम्ल है। मिट्टी की स्थितियों का परीक्षण करने के पश्चात् एक किसान पाता है कि उसे अपनी फसल के लिए 14 किग्रा नाइट्रोजन और 14 किग्रा फॉस्फोरिक अम्ल की आवश्यकता है। यदि F1 की कीमत Rs 6 /किग्रा और F2 की कीमत Rs 5/किग्रा है, प्रत्येक प्रकार का कितना उर्वरक उपयोग के लिए चाहिए ताकि न्यूनतम मूल्य पर वाँछित पोषक तत्त्व मिल सके। न्यूनतम लागत क्या है?
हल-
माना उर्वरक F1 = x किग्रा और उर्वरक F2 = y किग्रा
दिये गये आँकड़ों से निम्नलिखित सारणी बनाते हैं

इस रैखिक प्रोग्रामन समस्या का गणितीय रूप इस प्रकार होगा ।


B(100, 80) पर न्यूनतम लागत Rs 1000 हे।
क्योकि सुसंगत क्षेत्र अपरिबद्ध है इसीलिए Z का न्यूनतम मान 1000 हो सकता है या नहीं भी हो सकता।
इसलिए हम असमिका 6x + 5y < 1000 का आलेख खींचते हैं।
क्योंकि इस असमिका द्वारा निरूपित खुले अर्द्धतल और सुसंगत क्षेत्र में कोई भी बिन्दु उभयनिष्ठ नहीं है।
इसलिए Z का न्यूनतम मान = Rs 1000
जबकि उर्वरक F1, 100 किग्रा तथा उर्वरक F2, 80 किग्रा मिलाया जाता है।