UP Board Solutions for Class 10 Maths Chapter 1 Real Numbers
UP Board Solutions for Class 10 Maths Chapter 1 Real Numbers
प्रश्नावली 1.1
प्र. 1.
निम्नलिखित संख्याओं का HCF ज्ञात करने के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग कीजिए:
(i) 135 और 225
(ii) 196 और 38220
(iii) 867 और 255
हलः
प्र. 2.
दर्शाइए कि कोई भी धनात्मक विषम पूर्णांक 6q +1 या 6q +3 या 6q + 5 के रूप का होता है, जहाँ q कोई पूर्णाक है।
हलः
मान ‘a’ एक धनात्मक पूर्णाक है। को 6 से विभाजित करने पर भागफल q और शेष । प्राप्त होता है। .: यूक्लिड प्रमेयिका से,
प्र. 3.
किसी परेड में 616 सदस्यों वाली एक सेना (आर्मी) की टुकड़ी को 32 सदस्यों वाले एक आर्मी बैंड के पीछे | मार्च करना है। दोनों समूहों को समान संख्या वाले स्तंभों में मार्च करना है। उन स्तंभों की अधिकतम संख्या वाले स्तंभों में मार्च करना है। उन स्तंभों की अधिकतम संख्या क्या है, जिसमें वे मार्च कर सकते हैं?
हलः
प्र. 4.
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का वर्ग, किसी पूर्णांक m के लिए 3m या 3m +1 के रूप का होता है।
हलः
माना x एक धनात्मक पूर्णांक 3q, 3g + 1 या 3g + 2 के रूप में है।
प्र. 5.
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णांक का घन 9m, 9m + 1 या 9m +8 के रूप का होता है।
हलः
एक धनात्मक पूर्ण x की कल्पना करें कि यह 3q, (3q + 1) या (3q + 2) के रूप में है।
प्रश्नावली 1.2
प्र. 1.
निम्नलिखित संख्याओं को अभाज्य गुणनखंडों के गुणनफल के रूप में व्यक्त कीजिए।
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
हुलः
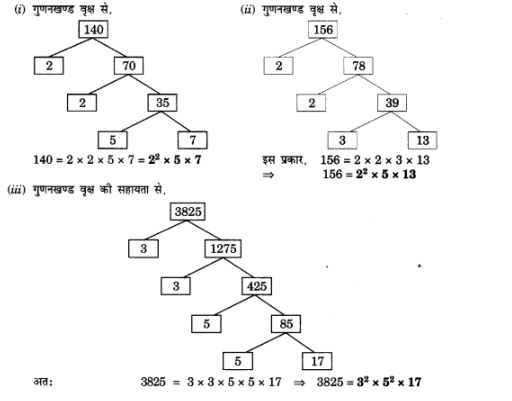
प्र. 2.
पूर्णाकों के निम्नलिखित युग्मों के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि वो संख्याओं को गुणनफल = HCF x LCM है।
(i) 28 और 91
(ii) 510 और 92
(iii) 336 और 64
हलः
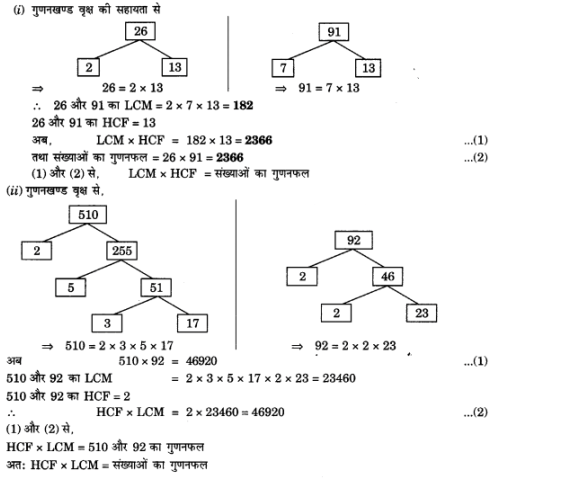
प्र. 3.
अभाज्य गुणनखण्डन विधि द्वारा निम्नलिखित पूर्णांकों के HCF और LCM ज्ञात कीजिए।
(i) 12, 15 और 21
(ii) 17, 23 और 29
(iii) 8, 9 और 25
हलः
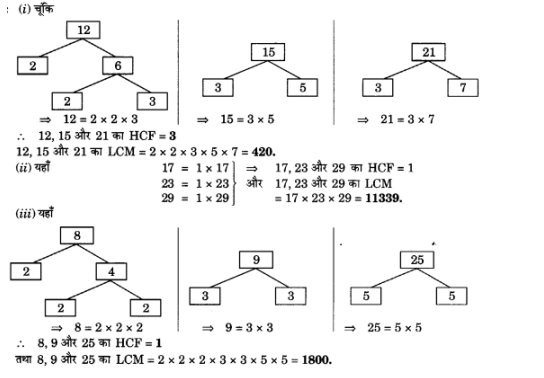
प्र. 4.
HCF (306, 657) = 9 दिया है। LCM (306, 657) ज्ञात कीजिए।
हलः
HCF (306, 657) अर्थात् 306 और 657 का HCF = 9
चूंकि LCM x HCF = संख्याओं का गुणनफल
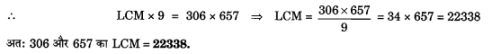
प्र. 5.
जाँच कीजिए कि क्या किसी प्राकृत संख्या n के लिए, संख्या 6″ अंक 0 पर समाप्त हो सकती है।
हुलः
यहाँ n एक प्राकृत संख्या है और माना 69 अंक 0 पर समाप्त होती है।
प्र. 6.
व्याख्या कीजिए कि 7 x 11 x 13 + 13 और 7×6 x 5x4x3 x 2 x 1+ 5 भाज्य संख्याएँ क्यों हैं।
हलः
प्र. 7.
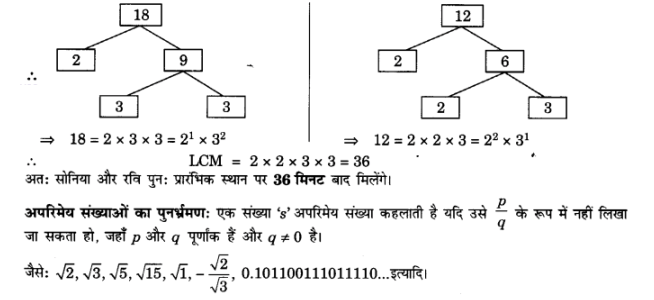
किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है। इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं। मान लीजिए वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारंभ करके एक ही दिशा में चलते हैं। कितने समय बाद वे पुनः प्रारंभिक स्थान पर मिलेंगे?
हलः
एक चक्कर लगाने में सोनिया का समय = 18 मिनट
एक चक्कर लगाने में रवि का समय = 12 मिनट
18 और 12 का LCM के समान समय के बाद वे पुनः प्रारंभिक स्थान पर मिलेंगे।
प्रश्नावली 1.3
प्र. 1.
सिद्ध कीजिए कि 5 एक अपरिमेय संख्या है।
हलः
प्र.2.
सिद्ध कीजिए कि 3+24/5 एक अपरिमेय संख्या है।
हलः
प्र. 3.
सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय हैं।
(a) [latex]\frac { 1 }{ \sqrt { 2 } } [/latex]
(b) [latex]7\sqrt { 5 }[/latex]
(c) [latex]6+\sqrt { 2 } [/latex]
हलः
परिमेय संख्याओं और उनके दशमलव प्रसारों का पुनर्भमण
प्रश्नावली 1.4
प्र. 1.
बिना लंबी विभाजन प्रक्रिया किए बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत हैं या असांत आवर्ती हैं।
(i) [latex s=2]\frac { 13 }{ 3125 } [/latex]
(ii) [latex s=2]\frac { 17 }{ 8 } [/latex]
(iii) [latex s=2]\frac { 64 }{ 455 } [/latex]
(iv) [latex s=2]\frac { 15 }{ 1600 } [/latex]
(v) [latex s=2]\frac { 29 }{ 343 } [/latex]
(vi) [latex s=2]\frac { 23 }{ { 2 }^{ 3 }{ 5 }^{ 2 } } [/latex]
(vii) [latex s=2]\frac { 129 }{ { 2 }^{ 2 }{ 5 }^{ 7 }{ 7 }^{ 5 } } [/latex]
(viii) [latex s=2]\frac { 6 }{ 15 } [/latex]
(ix) [latex s=2]\frac { 35 }{ 50 } [/latex]
(x) [latex s=2]\frac { 77 }{ 210 } [/latex]
हलः
चूंकि किसी भी परिमेय संख्या के हर के अभाज्य गुणनखण्डन में 2n, 5m के अतिरिक्त गुणनखण्ड नहीं हैं तो इसका दशमलव प्रसार सांत-दशमलव होता है अन्यथा यह असांत-आवर्ती दशमलव प्रसार होता है।
प्र. 2.
ऊपर दिए गए प्रश्न में उन परिमेय संख्याओं के दशमलव प्रसारों को लिखिए जो सांत हैं।
हलः
प्र. 3.
कुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि वह संख्या परिमेय संख्या है या नहीं। यदि यह परिमेय संख्या है और P के रूप की है तो q के अभाज्य गुणनखण्डों के बारे में आप क्या कह सकते हैं?
(i) 43.123456789
(ii) 0.120120012000120000
(iii) 43.123456789
हलः
(i) 43.123456789
चूंकि उक्त दशमलव प्रसार सांत है। .:. इसे [latex]\frac { p }{ q }[/latex] के रूप में व्यक्त किया जा सकता है।
The Complete Educational Website