UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 8 Index Numbers (सूचकांक)

पाठ्य-पुस्तक के प्रश्नोत्तर

प्रश्न 1.
मदों के सापेक्षिक महत्त्व को बताने वाले सूचकांक को
(क) भारित सूचकांक कहते हैं।
(ख) सरल समूहित सूचकांक कहते हैं।
(ग) सरल मूल्यानुपातों का औसत कहते हैं।
उत्तर
(क) भारित सूचकांक कहते हैं।

प्रश्न 2.
अधिकांश भारित सूचकांकों में भार का सम्बन्ध
(क) आधार वर्ष से होता है।
(ख) वर्तमान वर्ष से होता है।
(ग) आधार एवं वर्तमान वर्ष दोनों से होता है।
उत्तर
(ख) वर्तमान वर्ष से होता है।

प्रश्न 3.
ऐसी कंस्तु जिसका सूचकांक में कम भार है, उसकी कीमत में परिवर्तन से सूचकांक में कैसा परिवर्तन होगा
(क) कस
(ख) अधिक
(ग) अनिश्चित
उत्तर
(क) कम

प्रश्न 4.
कोई उपभोक्ता सूचकांक किस परिवर्तन को मापता है?
(क) खुदरा कीमत ।
(ख) थोक कीमत
(ग) उत्पादकों की कीमत
उत्तर
(क) खुदरा कीमत

प्रश्न 5.
औद्योगिक श्रमिकों के लिए उपभोक्ता कीमत सूचकांक में किस मद के लिए उच्चतम भार होता है?
(क) खाद्य पदार्थ
(ख) आवास
(ग) कपड़े
उत्तर
(क) खाद्य पदार्थ

प्रश्न 6.
सामान्यतः मुद्रा-स्फीति में परिकलन में किसका प्रयोग होता है?
(क) थोक कीमत सूचकांक
(ख) उपभोक्ता कीमत सूचकांक
(ग) उत्पादक कीमत सूचकांक
उत्तर
(क) थोक कीमत सूचकांक

प्रश्न 7.
हमें सूचकांक की आवश्यकता क्यों होती है?
उतर
सूचकांक सम्बन्धित चरों के समूह के परिमाण में परिवर्तनों को मापने का एक सांख्यिकीय साधन है। ये अर्थव्यवस्था के लिए बहुत उपयोगी होते हैं। निम्नलिखित कारणों से हमें सूचकांक की आवश्यकता होती है

मजदूरी तय करने, लगान, कर, आय नीति का निर्धारण, कीमत-निर्धारण एवं आर्थिक नीति बनाने | के लिए सूचकांक का प्रयोग किया जाता है।
उपभोक्ता कीमत सूचकांक (CPI) फुटकर (retail)-कीमतों में औसत परिवर्तन मापने के लिए आवश्यक होता है।
औद्योगिक उत्पादन सूचकांक (IPI) अनेक उद्योगों के औद्योगिक उत्पादन के स्तर में परिवर्तन को मापने में सहायक होता है।
थोक कीमत सूचकांक (WPI) सामान्य कीमत स्तर में परिवर्तन का संकेत देता है।
कृषि क्षेत्र की प्रगति का जायजा लेने के लिए कृषि उत्पादन सूचकांक (API) आवश्यक होता है।

प्रश्न 8.
आधार अवधि (आधार वर्ष) के वांछित गुण क्या होते हैं?
उत्तर
आधार अवधि (आधार वर्ष) के वांछित गुण निम्नलिखित होने चाहिए|

आधार वर्ष एक सामान्य वर्ष होना चाहिए, इस वर्ष असाधारण प्राकृतिक अथवा राजनीतिक घटनाएँ घटित न हुई हों।
आधार वर्ष में कीमत स्तर में असाधारण परिवर्तन न हुए हों।
यह वर्ष न तो अत्यधिक पुराना हो और न ही अत्यधिक नया।।
इस वर्ष में पर्याप्त एवं विश्वसनीय आँकड़े उपलब्ध होने चाहिए।

प्रश्न 9.
भिन्न उपभोक्ताओं के लिए भिन्न उपभोक्ता कीमत सूचकांकों की अनिवार्यता क्यों होती
उत्तर
भिन्न उपभोक्ताओं के उपभोग में व्यापक भिन्नताएँ पाई जाती हैं। इसलिए भिन्न उपभोक्ताओं के लिए भिन्न उपभोर्ग कीमत सूचकांक बनाए जाते हैं। भारत में तीन उपभोक्ता कीमत सूचकांक बनाए जाते

औद्योगिक श्रमिकों के लिए उपभोक्ता कीमत सूचकांक (आधार वर्ष 1982)
शहरी गैर-शारीरिक (मजदूर) कर्मचारियों के लिए उपभोक्ता कीमत सूचकांक (आधार वर्ष | 1984-85)
कृषि श्रमिकों के लिए उपभोक्ता कीमत सूचकांक (आधार वर्ष 1986-87)।

प्रश्न 10.
औद्योगिक श्रमिकों के लिए उपभोक्ता कीमत सूचकांक क्या मापता है?
उत्तर
भारत के औद्योगिक श्रमिकों के लिए अलग से उपभोक्ता कीमत सूचकांक बनाया जाता है। इसे 1982 को आधार वर्ष मानकर बनाया जाता है। इसका नियमित रूप से हर महीने परिकलन किया जाता है। यह सूचकांक औद्योगिक श्रमिकों के जीवन-निर्वाह पर फुटकर कीमतों में आए परिवर्तनों के प्रभावों को मापता है। इनका प्रकाशन श्रमिक केन्द्र शिमला द्वारा किया जाता है। इसका निर्माण करते समय औद्योगिक श्रमिकों के लिए मुख्य वस्तु समूहों को उपयुक्त भार दिया जाता है।

प्रश्न 11.
कीमत सूचकांक तथा मात्रा सूचकांक में क्या अन्तर है?
उत्तर
कीमत सूचकांक एक अभारित सूचकांक है। यह वस्तु की वर्तमान वर्ष की कीमत एक आधार वर्ष की कीमत का सरल अनुपात होता है। सूत्र रूप में,
${ p }_{ 01 }=\cfrac { { \Sigma p }_{ 1 } }{ { \Sigma p }_{ 0 } } \times 100$

यहाँ, P₀₁= कीमत सूचकांक
P₁ = वर्तमान वर्ष की कीमत
P₀ = आधार वर्ष की कीमत
मात्रा सूचकांक कीमत के स्थान पर उत्पादन की मात्रा का तुलनात्मक अध्ययन प्रस्तुत करता है। इस प्रकार के सूचकांक की रचना करते समय सर्वप्रथम मात्रा अनुपात ज्ञात किए जाते हैं। सूत्रानुसार,
$\cfrac { q1 }{ q0 } \times 100$
यहाँ, Q.R. = मात्रानुपात
q = वर्तमान वर्ष में उत्पादन की मात्रा
qo = आधार वर्ष में उत्पादन की मात्रा
इसके बाद प्रचलित वर्ष के सभी मात्रानुपातों का समान्तर माध्य निकाल लिया जाता है। यही मात्रा सूचकांक है।।

प्रश्न 12.
क्या किसी भी तरह की कीमत परिवर्तन एक कीमत सूचकांक में प्रतिबिम्बित होता है?
उत्तर
कीमत सूचकांक फुटकर कीमतों में परिवर्तनों के औसत को मापता है। यह किसी विशिष्ट कीमत परिवर्तन को प्रदर्शित नहीं करता है, जबकि प्रत्येक प्रकार की कीमत में परिवर्तन कीमत सूचकांक के मान को प्रभावित करता है।

प्रश्न 13.
क्या शहरी गैर-शारीरिक कर्मचारियों के लिए उपभोक्ता कीमत सूचकांक भारत के राष्ट्रपति के निर्वाह लागत में परिवर्तन का प्रतिनिधित्व कर सकता है?
उत्तर
नहीं, शहरी गैर-शारीरिक कर्मचारियों के लिए उपभोक्ता कीमत सूचकांक भारत के राष्ट्रपति के निर्वाह लागत में परिवर्तन का प्रतिनिधित्व नहीं कर सकता है।

प्रश्न 14.
नीचे एक औद्योगिक केन्द्र के श्रमिकों द्वारा 1980 एवं 2005 के दौरान निम्न मदों पर प्रति
व्यक्ति मासिक व्यय को दर्शाया गया है। इन मदों का भार क्रमशः 75, 10, 5, 6 तथा 4 है। 1980 को आधार मानकर 2005 के लिए जीवन-निर्वाह लागत का एक भारित सूचकांक तैयार कीजिए।

हल

$CPI=\cfrac { \Sigma wR }{ \Sigma W } =\cfrac { 18459.47 }{ 100 } =184.59$

प्रश्न 15.
निम्नलिखित सारणी को ध्यानपूर्वक पढिए एवं अपनी टिप्पणी कीजिए।

उत्तर
उपर्युक्त तालिका से निम्नलिखित बातें प्रतिबिम्बित होती हैं

विभिन्न उद्योगों, खनन एवं उत्खनन, विनिर्माण एवं विद्युत की संवृद्धि दरें भिन्न-भिन्न हैं। इनमें विनिर्माण क्षेत्र की संवृद्धि दर सबसे अधिक है, जबकि खनन एवं उत्खनन क्षेत्र की संवृद्धि दर सबसे कम है।
विभिन्न औद्योगिक क्षेत्रों को भिन्न-भिन्न भार दिए गए हैं। इनमें सबसे अधिक भार विनिर्माण क्षेत्र को तथा सबसे कम भार विद्युत क्षेत्र को दिया गया है।
सामान्य संवृद्धि दर खनन एवं उत्खनन तथा विद्युत क्षेत्र से अधिक है किन्तु विनिर्माण क्षेत्र से कम

प्रश्न 16.
अपने परिवार में उपभोग की जाने वाली महत्त्वपूर्ण मदों की सूची बनाने का प्रयास कीजिए।
उत्तर
हमारे परिवार में उपभोग की जाने वाली महत्त्वपूर्ण मदों की सूची
1. ईंधन एवं प्रकाश,
2. वस्त्र,
3. खाद्य-पदार्थ,
4. शिक्षा,
5. मकान का किरायी,
6. परिवहन,
7. मनोरंजन,
8. जूते-चप्पल,
9. फर्नीचर,
10. विविध

प्रश्न 17.
यदि एक व्यक्ति का वेतन आधार वर्ष में 4000 प्रतिवर्ष था और उसका वर्तमान वर्ष में वेतन १6000 है। उसके जीवन-स्तर को पहले जैसा ही बनाए रखने के लिए उसके वेतन में कितनी वृद्धि होनी चाहिए, यदि उपभोक्ता कीमत सूचकांक 400 हो।
उतर

वेतन में प्रतिशत बढ़ोतरी $\cfrac { 10000\times 100 }{ 6000 } =166.67$ %
जीवन-स्तर का समान स्तर कायम रखने हेतु वेतन में 166.67% वृद्धि होनी चाहिए।

प्रश्न 18.
जून 2005 में उपभोक्ता कीमत सूचकांक 125 था। खाद्य सूचकांक 120 तथा अन्य मदीं का सूचकांक 135 था। खाद्य-पदार्थों को दिया जाने वाला भार कुल भार का कितना प्रतिशत है? ।
उत्तर

प्रश्न 19.
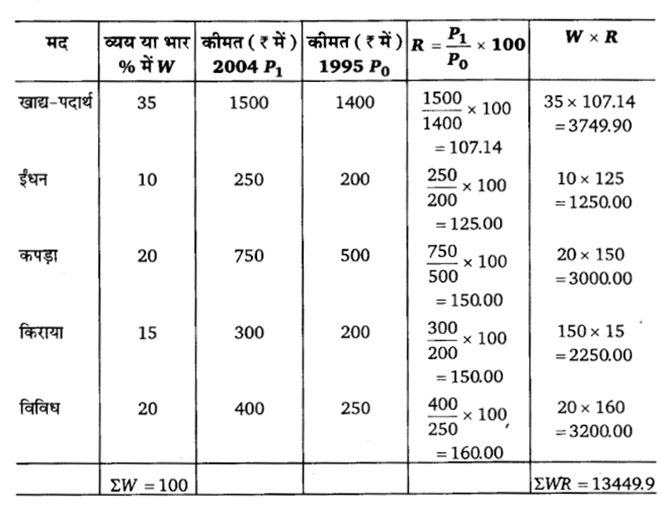
किसी शहर में एक मध्यवर्गीय पारिवारिक बजट में जाँच-पड़ताल से निम्नलिखित जानकारी प्राप्त होती है|

1995 की तुलना में 2004 में निर्वाह सूचकांक का मान क्या होगा?
हल

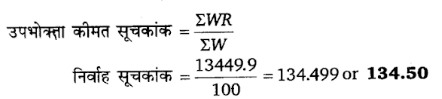
प्रश्न 20.
दो सप्ताह तक अपने परिवार के (प्रति इकाई) दैनिक व्यय, खरीदी गई मात्रा तथा दैनिक खरीददारी को अभिलेखित कीजिए। कीमत में आए परिवर्तन आपके परिवार को किस तरह से प्रभावित करते हैं?
उत्तर
स्वयं करें।

प्रश्न 21.
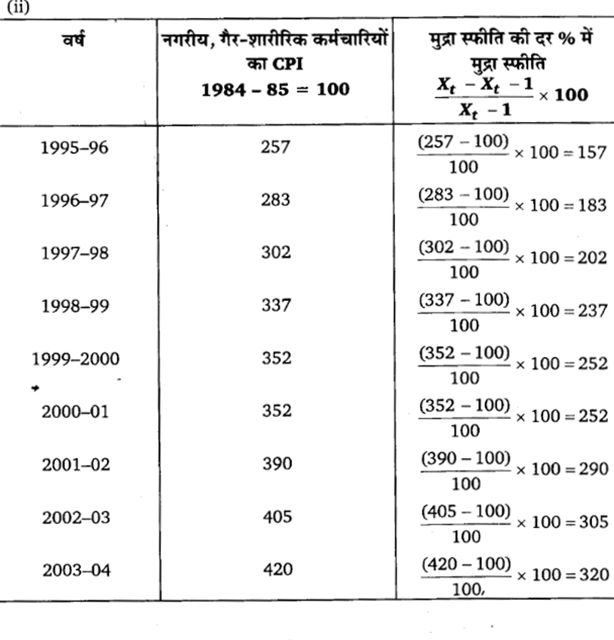
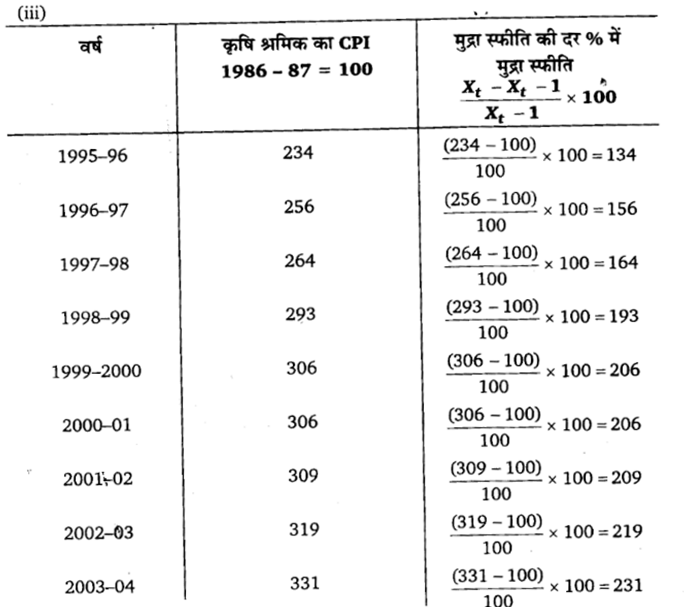
निम्नलिखित आँकड़े दिए गए हैं।

रस्रोत- आर्थिक सर्वेक्षण, भारत सरकार, 2004-2005.
(क) विभिन्न सूचकांकों को प्रयुक्त करते हुए मुद्रास्फीति की दर का परिकलन कीजिए।
(ख) सूचकांकों के सापेक्षिक मानों पर टिप्पणी कीजिए।
(ग) क्या ये तुलना योग्य हैं?
उत्तर
(क)(i)

(iv)

(ख) औद्योगिक श्रमिकों के लिए आधार वर्ष 1982 के साथ उपभोक्ता कीमत सूचकांक सबसे अधिक है। थोक मूल्य सूचकांक पूरी अवधि में सबसे कम है। (1993-96 से 2003-04 तक)
(ग) तालिका में दिए गए सूचकांक निम्नलिखित कारणों से तुलनात्मक नहीं हैं

आधार वर्ष अलग-अलग हैं।
विभिन्न सूचकांकों की मदें भिन्न हो सकती हैं।
अलग-अलग सूचकांकों के लिए विभिन्न मदों को भिन्न भार प्रदान किए जा सकते हैं।

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न
प्रश्न 1.
“कीमत क्य सूचकांक आधार-वर्ष की तुलना में किसी अन्य समय में कीमतों की औसत ऊँचाई को प्रकट करने वाली संख्या है।” यह परिभाषा दी है
(क) प्रो० चैण्डलर ने
(ख) प्रो० बाउले ने
(ग) किनले ने ।
(घ) हार्पर ने
उत्तर—
(क) प्रो० चैण्डलर ने

प्रश्न 2. सूचकांक की विशेषता नहीं है
(क) सूचकांक मुद्रा के मूल्य का निरपेक्ष माप न होकर सापेक्ष माप है।
(ख) सूचकांकों को प्रतिशतों में व्यक्त नहीं किया जाता है।
(ग) यह एक विशेष प्रकार का माध्य ही है।
(घ) सूचकांक आर्थिक पहलू के उच्चावचनों को संख्यात्मक रूप में ही माप सकता है।
उत्तर
(ख) सूचकांकों को प्रतिशतों में व्यक्त नहीं किया जाता है।

प्रश्न 3.
“सूचकांक की श्रेणी एक ऐसी श्रेणी होती है, जो अपने झुकाव तथा उच्चावचनों द्वारा जिस परिमाण से संबंधित है, में होने वाले परिवर्तनों को स्पष्ट करती है।”
(क) डॉ० बावले ने
(ख) चैण्डलर ने
(ग) होरेस सेक्राइस्ट ने
(घ) किनले ने
उत्तर
(ग) होरेस सेक्राइस्ट ने

प्रश्न 4.
श्रृंखला मूल्यानुपात

उत्तर

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
सूचकांक क्या है?
उत्तर
सूचकांक सम्बन्धित चरों के समूह के परिमाण में परिवर्तनों को मापने की एक सांख्यिकी विधि है।

प्रश्न 2.
सूचकांकों को किस रूप में व्यक्त किया जाता है?
उत्तर
सूचकांकों को प्रतिशत के रूप में व्यक्त किया जाता है।

प्रश्न 3.
आधार-वर्ष क्या है?
उत्तर
दो वर्षों में से जिस वर्ष को आधार मानकर तुलना की जाती है, उसे आधार-वर्ष कहते हैं।

प्रश्न 4.
कीमत सूचकांक का क्या उपयोग है?
उत्तर
कीमत सूचकांक कुछ वस्तुओं की कीमतों की माप करता है जिससे उनकी तुलना सम्भव हो जाती

प्रश्न 5.
परिमाणात्मक सूचकांक क्या मापते हैं? उत्तर–परिमाणात्मक सूचकांक उत्पादन की भौतिक मात्रा, निर्माण तथा रोजगार में परिवर्तन को मापते हैं। प्रश्न 6. उत्पार्दन सूचकांक किसका सूचक है?
उत्तर
उत्पादन सूचकांक अर्थव्यवस्था में उत्पादन के स्तर का सूचक होता है।

प्रश्न 7.
एक सरल समूहित कीमत सूचकांक का सूत्र बताइए।
उत्तर
${ p }_{ 01 }=\cfrac { { \Sigma }p_{ 1 } }{ { \Sigma p }_{ 2 } } \times 100$

प्रश्न 8.
एक भारित समूहित कीमत सूचकांक का सूत्र बताइए।
उत्तर
${ p }_{ 01 }=\cfrac { { \Sigma }p_{ 1 }{ q }_{ 1 } }{ { \Sigma p }_{ 2 }{ q }_{ 2 } } \times 100$

प्रश्न 9.
मूल्यानुपातों के भारित सूचकांक का सूत्र बताइए।
उत्तर
${ p }_{ 01 }=\cfrac { \Sigma W(\cfrac { { P }_{ 1 } }{ { P }_{ 2 } } )\times 100 }{ \Sigma w }$

प्रश्न 10.
उपभोक्ता कीमत सूचकांक क्या मापता है?
उत्तर
यह फुटकर कीमतों में औसत परिवर्तन को मापता है।

प्रश्न 11.
उपभोक्ता कीमत सूचकांक बनाने की क्या उपयोगिता है?
उत्तर
उपभोक्ता कीमत सूचकांक (CPI) मजदूरी समझौता, आय-नीति, कीमत-नीति, किराया नियन्त्रण, कराधान तथा सामान्य आर्थिक नीतियों के निर्माण में सहायक होते हैं।

प्रश्न 12.
थोक कीमत सूचकांक का प्रयोग सामान्यतः किसलिए किया जाता है?
उत्तर
थोक कीमत सूचकांक (WPI) का प्रयोग सामान्य रूप से मुद्रा स्फीति को मापने के लिए किया जाता है।

प्रश्न 13.
मुद्रा की क्रय शक्ति एवं वास्तविक मजदूरी के परिकलन के लिए किस सूचकांक का प्रया किया जाता है?
उत्तर
उपभोक्ता कीमत सूचकांक।

प्रश्न 14.
औद्योगिक उत्पादन सूचकांक की क्या उपयोगिता है?
उत्तर
औद्योगिक उत्पादन सूचकांक हमें औद्योगिक क्षेत्र में उत्पादन में परिवर्तन के बारे में परिमाणात्मक अंक प्रदान करता है।

प्रश्न 15.
कृषि उत्पादन सूचकांक का क्या उपयोग है।
उत्तर
कृषि उत्पादन सूचकांक हमें कृषि क्षेत्र के निष्पादन के बारे में बताते हैं।

प्रश्न 16.
सेंसेक्स क्या है?
उत्तर
सेंसेक्स वह सूचक है जो कि भारतीय स्टॉक बाजार में होने वाले परिवर्तनों को दर्शाता है। इसका आधार-वर्ष 1978-79 है।

प्रश्न 17.
सूचकांकों की दो विशेषताएँ बताइए।
उत्तर

सूचकांक मुद्रा के मूल्य का निरपेक्ष माप न होकर सापेक्ष माप है।
सूचकांकों को प्रतिशतों में व्यक्त किया जाता है।

प्रश्न 18.
सूचकांकों के दो लाभ बताइए।
उत्तर

सामान्य मूल्य-स्तर में होने वाले परिवर्तनों को मापने के लिए सूचकांकों का प्रयोग किया जाता
सूचकांक वास्तविक आय में होने वाले परिवर्तन का सूचक होता है।

प्रश्न 19.
सूचकांकों की दो सीमाएँ बताइए।
उत्तर

सूचकांके निरपेक्ष परिवर्तनों की मापों की अपेक्षा सापेक्ष परिवर्तनों की ही माप करता है।
विभिन्न सूचकांक अलग-अलग उद्देश्यों को पूरा करते हैं।

प्रश्न 20.
फिशर का आदर्श सूचकांक का सूत्र बताइए।
उत्तर
Fisher’s Ideal index
$No.\sqrt { \cfrac { { \Sigma p }_{ 1 }{ q }_{ 0 } }{ \Sigma { p }_{ 0 }{ q }_{ 0 } } \times \cfrac { { \Sigma { p }_{ 1 } }{ q }_{ 1 } }{ \Sigma { p }_{ 0 }{ q }_{ 1 } } } \times 100$

लघु उत्तरीय प्रश्न

प्रश्न 1.
सूचकांकों की विशेषताएँ बताइए।
उत्तर
सूचकांकों की निम्नलिखित विशेषताएँ होती हैं

सूचकांक मुद्रा के मूल्य का निरपेक्ष माप न होकर सापेक्ष माप है।
सूचकांकों को प्रतिशतों में व्यक्त किया जाता है।
इनका प्रयोग ऐसे तथ्यों के परिवर्तनों को मापने के लिए किया जाता है, जिन्हें प्रत्यक्ष माप से नहीं मापा जा सकता।
यह एक विशेष प्रकार का माध्य ही है।
सूचकांक आर्थिक पहलू के उच्चावचों को संख्यात्मक रूप में ही माप सकता है।

प्रश्न 2.
सूचकांकों के प्रमुख लाभ (उपयोगिता) बताइए।
उत्तर
सूचकांकों के कुछ महत्त्वपूर्ण लाभ निम्नलिखित हैं-

सूचकांकों द्वारा समय-समय पर कीमत स्तर में होने वाले परिवर्तन या मुद्रा के मूल्य की क्रय शक्ति में होने वाले परिवर्तन को मापा जा सकता है।
सूचकांकों की सहायता से समाज में जीवन-स्तर के परिवर्तन का ज्ञान होता है। ये वास्तविक आय में परिवर्तन के बारे में जानकारी प्रदान करते हैं।
इनकी सहायता से वेतन-भत्तों में परिवर्तन करके वास्तविक आय को स्थिर रखने का प्रयास किया जाता है।
व्यापारी व उत्पादक़ कीमत स्तर के परिवर्तन के अनुसार ही अपने उत्पादन तथा व्यापार की योजनाएँ तैयार करते हैं।
आर्थिक स्थिति को ज्ञान प्राप्त करके ही आर्थिक नीतियों का निर्धारण किया जाता है। “
सूचकांकों के आधार पर ही सरकार मौद्रिक व राजकोषीय नीति का प्रारूप तैयार करती है।

प्रश्न 3.
‘फिशर का सूचकांक एक आदर्श सूचकांक है।’ इस कथन के समर्थन में अपने तर्क दीजिए।
उत्तर
‘फिशर का सूचकांक एक आदर्श सूचकांक है। इसके पक्ष में निम्नलिखित तर्क दिए जा सकते हैं

यह परिवर्तनशील भारों पर आधारित है।
इसमें आधार-वर्ष व चालू वर्ष दोनों की मात्राओं तथा मूल्यों को शामिल किया जाता है।
यह गुणोत्तर माध्य पर आधारित है।
यह ‘समय व्युत्क्रम परीक्षण’ तथा ‘तत्त्व व्युत्क्रम परीक्षण’ दोनों को पूरा करता है।

प्रश्न 4.
सूचकांक कितने प्रकार के होते हैं?
उत्तर
उद्देश्य के आधार पर सूचकांकों को दो भागों में बाँटा जा सकता है
1. थोक मूल्य सूचकांक तथा
2. जीवन-निर्वाह व्यय सूचकांक।
1. थोक मूल्य सूचकांक-
ये सूचकांक थोक मूल्यों के परिवर्तनों को प्रकट करने के लिए बनाए जाते हैं। इसमें किसी भी सामान्य वर्ष को आधार मानकर किसी भी अन्य चालू अवधि या अवधियों के मूल्यों में परिवर्तनों का अध्ययन किया जाता है। कुछ प्रतिनिधि वस्तुओं को चुनकर उनके थोक मूल्य लिए जाते हैं, आधार-वर्ष के मूल्यों को 100 मानकर चालू वर्ष या वर्षों के मूल्यानुपात (Price Relatives) निकाले जाते हैं तथा उनका माध्य ज्ञात किया जाता है। औसत मूल्यानुपात में परिवर्तन सामान्य मूल्य-स्तर में परिवर्तन को प्रदर्शित करते हैं।

2. जीवन-
निर्वाह व्यय सूचकांक-जीवन-निर्वाह व्यय सूचकांक किसी स्थान विशेष पर वर्ग विशेष के व्यक्तियों के निर्वाह व्यय में होने वाले परिवर्तनों की दिशा व मात्रा को प्रकट करते हैं। अत: इस सूचकांक को बनाने में उस विशिष्ट वर्ग द्वारा प्रयोग की जाने वाली प्रतिनिधि वस्तुओं को लेते हैं तथा उने सही फुटकर मूल्य ज्ञात करते हैं। विभिन्न वस्तुओं को उनके जीवन-निर्वाह में महत्त्व के अनुसार उचित भारांकन भी किया जाता है।

प्रश्न 5.
सूचकांक की रचना करते समय किन-किन बातों को ध्यान में रखना चाहिए?
उत्तर
सूचकांक की रचना करते समय निम्नलिखित बातों को ध्यान में रखना चाहिए

सूचकांक का उद्देश्य स्पष्ट होना चाहिए।
सूचकांक के लिए मदों का चयन सावधानीपूर्वक किया जाना चाहिए ताकि ये उनका प्रतिनिधित्व कर सकें।
आधार-वर्ष एक सामान्य वर्ष होना चाहिए और इसे नियमित रूप से अद्यतन किया जाना चाहिए।
उद्देश्य के अनुरूप सूत्र को चयन किया जाना चाहिए।
आँकड़ों के संग्रह में उचित सावधानी बरती जानी चाहिए।

प्रश्न 6.
संवेदी सूचकांक (Sensex) क्या है?
उत्तर
संवेदी सूचकांक (Sensex) वह सूचक है जो कि भारतीय स्टॉक बाजार में होने वाले परिवर्तनों को दर्शाता है। यह मुम्बई स्टॉक एक्सचेंज संवेदी सूचकांक का संक्षिप्त रूप है। इसका आधार वर्ष 1978-79 है। संवेदी सूचकांक का मान इस अवधि के सन्दर्भ में होता है। इसके अन्तर्गत 30 स्टॉक हैं जो अर्थव्यवस्था .के 13 क्षेत्रकों का प्रतिनिधित्व करते हैं। संवेदी सूचकांक का ऊपर चढ़ना यह बताता है कि अर्थव्यवस्था की दशा अच्छी है, बाजार ठीक चल रहा है और निवेशकों के लाभ बढ़ रहे हैं। इसके विपरीत, सूचकांक का नीचे आना शेयर धारकों की हानि का सबब बनता है।

प्रश्न 7.
फिशर का आदर्श सूचकांक ‘समय उत्क्राम्यता परीक्षण पर कैसे खरा उतरता है?
उत्तर
समय उत्क्राम्यता परीक्षण के अनुसार यदि आधार-वर्ष के आधार पर प्रचलित वर्ष का सूचकांक (Poi) निकाला जाए और फिर प्रचलित वर्ष के आधार पर प्रचलित वर्ष का सूचकांक (Po) ज्ञात किया जाए तो ये दोनों एक-दूसरे के व्युत्क्रम होंगे अर्थात् इन दोनों का गुणनफल 1 होगा। सूत्रानुसार,

प्रश्न 8.
फिशर का आदर्श सूचकांक ‘तत्त्व उत्क्राम्यता परीक्षण पर कैसे खरा उतरता है?
उत्तर
तत्त्व क्राम्यता परीक्षण-इस परीक्षण के अनुसार, यदि ‘मूल्य’ के स्थान पर ‘मात्रा’ और ‘मात्रा के स्थान पर ‘मूल्य’ रखकर सूचकांक (q₀₁) तैयार किया जाए तो उसका और मूल्य सूचकांक poi का गुणनफल चालू वर्ष के कुल मूल्य (Σp₁q₁) और आधार-वर्ष के कुल मूल्य (Σp₀q₀) के अनुपात के बराबर होना चाहिए।
सूत्रानुसार,

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
सूचकांक क्या है? इनकी उपयोगिता तथा सीमाओं का वर्णन कीजिए।
उत्तर
सूचकांक : अर्थ एवं परिभाषाएँ
समाज में वस्तुओं तथा सेवाओं की कीमतों में सदैव परिवर्तन होते रहते हैं। वस्तुओं और सेवाओं की कीमतों में परिवर्तन होने के कारण मुद्रा का मूल्य भी परिवर्तित होता रहता है, जिससे समाज का प्रत्येक वर्ग प्रभावित होता है, फलस्वरूप कीमत-स्तर, उपभोग, जनसंख्या, बचत, निवेश, राष्ट्रीय आय, आयात-निर्यात, मजदूरी, ब्याज, किराया व लगान आदि चरों में सदैव परिवर्तन होते रहते हैं। अत: मुद्रा-मूल्य में हुए परिवर्तनों का माप करना व्यावहारिक दृष्टि से अत्यधिक महत्त्वपूर्ण व उपयोगी है। इन परिवर्तनों को निरपेक्ष रूप से मापने का कोई साधन नहीं है; अतः इनको सापेक्ष माप लिया जाता है। सूचकांक विशिष्ट प्रकार के सापेक्ष माप होते हैं, जिनके आधार पर समंकों की उचित एवं स्पष्ट तुलना की जा सकती है।

सूचकांकों की प्रमुख परिभाषाएँ निम्नलिखित हैं

चैण्डलर के अनुसार-“कीमत का सूचकांक आधार-वर्ष की तुलना में किसी अन्य समय में कीमतों की औसत ऊँचाई को प्रकट करने वाली संख्या है।”
डॉ० बाउले के शब्दों में- “सूचकांक की श्रेणी एक ऐसी श्रेणी होती है, जो अपने झुकाव तथा उच्चावचनों द्वारा जिस परिमाण से संबंधित है, में होने वाले परिवर्तनों को स्पष्ट करती है।”
किनले के शब्दों में- “सूचकांक वह अंक है, जो किसी पूर्व निश्चित तिथि को चुनी वस्तुओं या | वस्तु-समूह के मूल्य का प्रतिनिधित्व करता है, जिसे प्रामाणिक मानते हुए किसी बाद की तिथि को | उन्हीं वस्तुओं के मूल्य से तुलना करते हैं।”
क्रॉक्सटन व काउडेन के अनुसार- “सूचकांक, संबंधित चर-मूल्यों के आकार में होने वाले |. अंतरों की माप करने के साधन हैं।”
होरेस सेक्राइस्ट के शब्दों में- “सूचकांक अंकों की एक ऐसी श्रेणी है, जिसके द्वारा किसी भी तथ्य के परिमाण में होने वाले परिवर्तनों का समय या स्थान पर मापन किया जा सकता है।”

सूचकांकों की विशेषताएँ
उपर्युक्त परिभाषाओं के आधार पर सूचकांकों की निम्नलिखित विशेषताएँ स्पष्ट होती हैं-

सूचकांक मुद्रा के मूल्य का निरपेक्ष माप न होकर सापेक्ष माप है। ”
सूचकांकों को प्रतिशतों में व्यक्त किया जाता है।
इनका प्रयोग ऐसे तथ्यों के परिवर्तनों को मापने के लिए किया जाता है, जिन्हें प्रत्यक्ष माप से नहीं मापा जा सकता।
यह एक विशेष प्रकार का माध्य ही है।
सूचकांक आर्थिक पहलू के उच्चावचनों को संख्यात्मक रूप में ही माप सकता है।

सूचकांक की उपयोगिता

सूचकांकों की सार्वभौमिक उपयोगिता है। ये व्यापारी, अर्थशास्त्री व राजनीतिज्ञों का पथ-प्रदर्शन करते हैं। और उन्हें भावी प्रवृत्तियों का अनुमान लगाने में सहायता करते हैं। कीमत, जीवन-निर्वाह, औद्योगिक उत्पादन, खाद्यान्न उत्पादन, निर्यात, आयात, लाभ, मुद्रा-पूर्ति, जनसंख्या, राष्ट्रीय आय, बजट घाटा अथवा आधिक्य आदि से संबंधित सूचकांक विभिन्न घटनाओं का सापेक्षिक माप प्रस्तुत करते हैं, इसीलिए सूचकांक ‘आर्थिक वायुमापक यंत्र’ (Economic Barometers) कहलाते हैं। व्यावहारिक रूप में सूचकांकों से निम्नलिखित लाभ प्राप्त होते हैं

मुद्रा के मूल्य की माप- सामान्य मूल्य-स्तर में होने वाले परिवर्तनों को मापने के लिए सूचकांकों का प्रयोग किया जाता है। सामान्य मूल्य-स्तर में होने वाले परिवर्तन से मुद्रा की क्रय-शक्ति में होने वाले परिवर्तनों का अनुमान लगाया जा सकता है।
आर्थिक स्थिति की तुलना—रहन-सहन संबंधी सूचकांकों की तुलना करके समाज के किसी | वर्ग के रहन-सहने में होने वाले परिवर्तनों का अनुमान लगाया जा सकता है।
मजदूरी निर्धारण में उपयोगिता– सूचकांक वास्तविक आय में होने वाले परिवर्तन का सूचक होता है। अतः मजदूरी व वेतन के निर्धारण में इनसे बहुत अधिक सहायता मिलती है। ”
ऋणों के न्यायपूर्ण भुगतान का आधार- सूचकांकों की सहायता से मूल्य-स्तर में परिवर्तन का अनुमान लगाया जा सकता है और इसी आधार पर ऋणों की मात्रा में परिवर्तन करके उनका न्यायपूर्ण भुगतान किया जा सकता है। इससे किसी भी पक्ष को असंगत लाभ या हानि नहीं होती।
अंतर्राष्ट्रीय तुलना करने में सहायक- सूचकांकों की सहायता से विभिन्न प्रकार की अंतर्राष्ट्रीय तुलनाएँ करना संभव है। विभिन्न देशों की मुद्राओं की क्रय-शक्ति में क्या परिवर्तन जहुए हैं, इसकी जानकारी व तुलना सूचकांकों की सहायता से की जा सकती है।
देश के आर्थिक विकास का अनुमान- उत्पादन सुचकांक देश में उत्पादन संबंधी जानकारी देते हैं, जिनके आधार पर सरकार अपनी औद्योगिक नीति का निर्माण करती हैं सूचकांकों की सहायता से ही विदेशी व्यापार की स्थिति व देश में पूँजी व विनियोग की मात्रा को ज्ञान होता है।
भावी प्रवृत्तियों का अनुमान- सूचकॉक न केवल वर्तमान परिवर्तनों को बताते हैं बल्कि इनकी सहायता से भविष्य के संबंध में भी महत्त्वपूर्ण अनुमान लगाए जा सकते हैं।
जटिल तथ्यों को सरल बनाना– सूचकांकों की सहायता से ऐसे जटिल तथ्यों में होने वाले परिवर्तनों की माप भी की जा सकती है, जिनकी माप किसी अन्य साधन से संभव नहीं है।
नियंत्रण एवं नीतियाँ- सूचकांकों के आधार पर ही सरकार आर्थिक नियोजन व नियंत्रण संबंधी नीतियाँ बनाती है।

सूचकांकों की सीमाएँ

सबसे अधिक उपयोगी सांख्यिकीय विधि होते हुए भी सूचकांक परिवर्तनों की एक अपूर्ण माप है। इसकी प्रमुख सीमाएँ निम्मलिखित हैं

सापेक्ष परिवर्तनों की अनुमानित माप- सूचकांक निरपेक्ष परिवर्तनों की मापों की अपेक्षा सापेक्ष परिवर्तनों की ही माप करता है और वह भी मात्र अनुमान के रूप में। वास्तव में, सूचकांक केवल सामान्य प्रवृत्तियों की ओर ही संकेत करते हैं।
शुद्धता की कमी- सूचकांक बनाते समय समूह की प्रत्येक इकाई को शामिल नहीं किया जाता है। वरन् इसके लिए कुछ प्रतिनिधि इकाइयों का ही चयन किया जाता है। इससे प्रतिदर्श अपर्याप्त और अप्रतिनिधि परिणामों की सत्यता कम हो जाती है।
उद्देश्य में अंतर- विभिन्न सूचकांक अलग-अलग उद्देश्यों को पूरा करते हैं। एक सूचकांक, जो एक उद्देश्य के लिए उपयुक्त हो सकता है, अन्य उद्देश्यों के लिए अनुपयुक्त हो सकता है।कोई भी सूचकांक सार्व-उद्देशीय नहीं होता।
अंतर्राष्ट्रीय तुलना कठिन- सूचकांकों की सहायता से दो देशों के संबंध में किसी प्रकार की तुलना करना काफी कठिन होता है क्योंकि सूचकांकों की निर्माण-विधि, उनका आधार-वर्ष तथाप्रतिनिधि वस्तुओं की सूची विभिन्न देशों में भिन्न-भिन्न होती है।
विभिन्न समय में तुलना करना कठिन– लोगों के द्वारा उपभोग की जाने वाली वस्तुओं में | परिवर्तन होता रहता है। अतः सूचकांकों की सहायता से विभिन्न समयों में तुलना करना संभव नहींहोता है।
भार निर्धारण अवैज्ञानिक- भारित सूचकांकों में भार निर्धारण मनमाना तथा अवैज्ञानिक होता है। भिन्न-भिन्न वर्षों में एक ही वस्तु के भार बदल जाते हैं, जिसके कारण परिणामों में अंतर आ जाता है।

प्रश्न 2.
सूचकांक रचना संबंधी समस्याओं का विवेचन कीजिए।
उत्तर
सूचकांक रचना संबंधी प्रमुख समस्याएँ निम्नलिखित हैं
1. सूचकांक का उद्देश्य,
2. पदों या वस्तुओं का चुनाव,
3. मूल्य उद्धरण,
4. आधार-वर्ष का चुनाव और सूचकांकों का परिगणन,
5. माध्य का चुनाव,
6. भारांकन विधि।।
1. सूचकांक का उद्देश्य
सूचकांक रचना से पूर्व उसके उद्देश्य को निश्चित कर लेना चाहिए क्योंकि वस्तुओं के चुनाव, उनके मूल्य उद्धरण तथा भारांकन आदि का निर्धारण सूचकांक के उद्देश्य पर ही निर्भर करता है। उदाहरण के लिए एक सूक्ष्मग्राही मूल्य सूचकांक में केवल उन वस्तुओं का समावेश किया जाना चाहिए, जिनके मूल्यों में तेजी से परिवर्तन होते रहते हैं। इसके विपरीत, सामान्य उद्देश्य वाले मूल्य सूचकांक में अधिकाधिक वस्तुओं का समावेश किया जाना चाहिए ताकि वह समाज में सभी वर्गों का सही-सही प्रतिनिधित्व कर सके।

2. पदों या वस्तुओं का चुनाव
चूंकि किसी भी एक सूचकांक में समस्त पदों या वस्तुओं का चुना जाना संभव नहीं है; अत: कुछ प्रतिनिधि वस्तुओं का चुनाव कर लिया जाना चाहिए। इस संबंध में उठने वाले स्वाभाविक प्रश्न इस प्रकार हैं
(अ) कौन-सी वस्तुएँ चुनी जाएँ- चुनी जाने वाली वस्तुओं में निम्नलिखित गुण होने चाहिए|

वस्तुएँ ऐसी होनी चाहिए, जो अपने वर्ग का सच्चे अर्थों में प्रतिनिधित्व कर सकें।
वस्तुएँ ऐसी होनी चाहिए, जो सरलता से पहचानी जा सकें तथा जिनका स्पष्ट रूप से वर्णन किया | जा सके।
चुनी हुई वस्तुएँ प्रमापित व एकरूप होनी चाहिए।
वस्तुएँ लोकप्रिय होनी चाहिए।

(ब) वस्तुओं की संख्या कितनी हो-सामान्यत:
सूचकांक में जितनी अधिक वस्तुएँ सम्मिलित की जाएँगी, वह उतना ही अधिक शुद्ध व विश्वसनीय माना जाएगा, परंतु बहुत अधिक वस्तुओं को सूचकांक में सम्मिलित करना भी संभव नहीं है। वास्तव में, संख्या का निर्धारण सूचकांक के उद्देश्य, उपलब्ध समय, धन तथा वांछित शुद्धता पर अधिक निर्भर करता है। सामान्य परम्परा यह है कि सूचकांक में 25 से 50 वस्तुओं तक का चयन किया जाता है।

(स) वस्तुएँ किस किस्म की हों
सूचकांकों में ऐसी किस्म की वस्तुएँ शामिल की जानी चाहिए, जो सबसे अधिक प्रचलित हों; प्रमापित हों तथा गुणों में स्थिर हों।

(द) वस्तुओं का किस प्रकार वर्गीकरण किया जाए-
चुनी हुई वस्तुओं को सजातीयता के आधार पर कुछ निश्चित वर्गों और उपवर्गों में विभाजित कर देना चाहिए, जिससे सम्पूर्ण मूल्य सूचकांक के साथ-साथ वर्ग सूचकांक भी ज्ञात हो जाए।

3. मूल्य उद्धरण
मूल्य उद्धरण लेते समय निम्नलिखित बातों का विशेष ध्यान रखना चाहिए
(अ) थोक या फुटकर मूल्य सामान्यतः
मूल्य सूचकांकों की रचना में वस्तुओं के थोक मूल्य ही लिए जाते हैं क्योंकि वे फुटकर मूल्यों की अपेक्षा कम परिवर्तनशील होते हैं, स्थान-स्थान के आधार पर उनमें कम अंतर होते हैं और उन्हें ज्ञात करना भी सरल होता है।

(ब) द्रव्य-मूल्य अथवा वस्तु-मूल्य-
सूचकांकों के लिए मूल्य उद्धरण द्रव्य के रूप में ही व्यक्त किए। जाने चाहिए, वस्तुओं के परिमाण के रूप में नहीं। यदि मूल्य उद्धरण वस्तु-मूल्य के रूप में हों तो उन्हें पहले द्रव्य-मूल्यों के रूप में बदल लेना चाहिए।

(स) मूल्य उद्धरणों की संख्या व आवृत्ति– सूचकांक निर्माण से पूर्व यह भी तय कर लेना चाहिए,कि मूल्य कितनी बार और किस अंतराल में लिए जाने हैं। मूल्य उद्धरणों की आवृत्ति सूचकांक के उद्देश्य, अवधि, उपलब्ध साधन व शुद्धता के स्तर पर निर्भर होती है।

(द) मूल्य उद्धरण प्राप्ति के स्थान व साधन- मूल्य उन मण्डियों से प्राप्त किए जाने चाहिए, जहाँ पर वस्तुओं का बड़ी मात्रा में क्रय-विक्रय होता हो लेकिन जीवन-निर्वाह व्यय सूचकांक बनाने के लिए उसी स्थान के मूल्यों को प्राप्त करना चाहिए। मूल्य उद्धरण के स्रोत निष्पक्ष, विश्वसनीय तथा उपयुक्त होने चाहिए।

4. आधार-वर्ष का चुनाव और सूचकांकों का परिगणन
आधार-वर्ष से हमारा आशय उस वर्ष विशेष से होता है, जिसको आधार मानकर हम आर्थिक क्रियाकलापों की तुलना करते हैं। अतः आधार-वर्ष का चुनाव अत्यंत सतर्कतापूर्वक करना चाहिए। यथासंभव आधार-वर्ष

सामान्य होना चाहिए,
वास्तविक होना चाहिए,
उस काल की समस्त सूचनाएँ उपलब्ध होनी चाहिए तथा
वह वर्ष अधिक पुराना नहीं होना चाहिए। आधार वर्ष निश्चित करने की निम्नलिखित दो रीतियाँ हैं

(अ) स्थिर आधार रीति,
(ब) श्रृंखला आधार रीति।
(अ) स्थिर आधार रीति–इस रीति के अनुसार सर्वप्रथम एक सामान्य वर्ष चुन लिया जाता है और फिर अन्य वर्षों के मूल्य-स्तर की तुलना उस स्थिर वर्ष के आधार पर की जाती है। स्थिर आधार-वर्षे दो प्रकार का हो सकता है

एकवर्षीय आधार-एकवर्षीय आधार में जो वर्ष आधार-वर्ष के रूप में चुना जाता है, अन्ये वर्षों के मूल्यों की तुलना उस स्थिर वर्ष के आधार पर की जाती है।
बहुवर्षीय मध्य आधार-कभी-कभी कोई अंक वर्ष ऐसा नहीं होता, जो सामान्य हो और जिसे स्थिर आधार माना जा सके। ऐसी दशा में अनेक ऐसे वर्ष छाँट लिए जाते हैं, जिनमें कम उतार-चढ़ाव हुए हों और फिर उन वर्षों के मूल्य-स्तर का समान्तर माध्य निकालकर उन माध्य मूल्यों को आधार माना जाता है।

आधार- वर्ष को निश्चित कर लेने के उपरांत चालू वर्ष के सूचकांक तैयार करने के लिए मूल्यानुपात निकाले जाते हैं। इसके लिए आधार-वर्ष के मूल्य को 100 मानकर, चालू वर्ष के मूल्यों का निकाला गया प्रतिशत मूल्यानुपात’ कहलाता है।
सूत्रानुसार,

5. माध्य का चुनाव
सूचकांक विभिन्न वस्तुओं के मूल्यानुपातों का माध्य है। अतः यह निर्धारित करना आवश्यक है कि सूचकांक रचना में किस माध्ये का प्रयोग किया जाए। व्यवहार में माध्यिका समान्तर माध्य अथवा गुणोत्तर माध्य में से किसी एक का प्रयोग करना उपयुक्त रहता है।

6. भारांकन विधि
व्यवहार में भिन्न-भिन्न वस्तुओं का भिन्न-भिन्न सापेक्षिक महत्त्व होता है। उदाहरण के लिए उपभोग के क्षेत्र में लोहे की तुलना में नमक का महत्त्व अधिक है। इसी प्रकार उत्पादन के क्षेत्र में टी०वी० की तुलना में कपड़े का महत्त्व अधिक है। अत: विभिन्न वस्तुओं अथवा पदों के तुलनात्मक महत्त्व को प्रकट करने के लिए किसी सुनिश्चित आधार पर भारों का प्रयोग किया जाता है। ऐसे सूचकांक ‘भारित सूचकांक कहलाते हैं।

प्रश्न 3.
साधारण सूचकांक रचना की

सरल समूहीकरण विधि व
सरल मूल्य अनुपात माध्य विधि को उदाहरणों की सहायता से समझाइए।

उत्तर
साधारण सूचकांक बनाने की दो मुख्य विधियाँ हैं|
1. सरल समूहीकरण विधि (Simple Aggregative Method),
2. सरल मूल्य अनुपात विधि (Simple Average of Price Relative Method)। 1. सरल समूहीकरण विधि-इस विधि में प्रचलित वर्ष के विभिन्न वस्तुओं के मूल्यों के जोड़ को आधार वर्ष के जोड़ से भाग देकर 100 से गुणा कर दिया जाता है। सूत्र रूप में,
${ p }_{ 01 }=\cfrac { \Sigma { p }_{ 1 } }{ { \Sigma p }_{ 0 } } \times 100$

यहाँ, P₀₁ = वर्तमान वर्ष का मूल्य सूचकांक |
∑P₁ = वर्तमान वर्ष की विभिन्न वस्तुओं के मूल्यों का योग
∑P₀= आधारे-वर्ष की उन्हीं वस्तुओं के मूल्यों का योग
उदाहरण
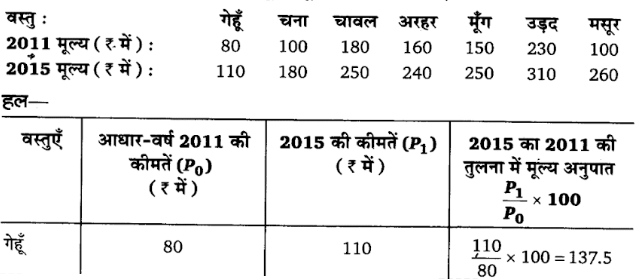
1. निम्नांकित आँकड़ों से सरल समूहीकरण विधि द्वारा 2011 को आधार-वर्ष मानकर वर्ष 2015 के मूल्य सूचकांक तैयार कीजिए।
वस्तुएँ :

यह विधि अत्यंत सरल है किंतु इस विधि का प्रयोग तभी किया जाना चाहिए जब सभी वस्तुओं के मूल्य एक ही इकाई के रूप में व्यक्त किए गए हों। अन्यथा निकाले गए निष्कर्ष भ्रामक होंगे।

2. सरल मूल्य अनुपात माध्य विधि— इस विधि के अनुसार सबसे पहले प्रत्येक वस्तु का मूल्य अनुपात निकाला जाता है। किसी वस्तु का मूल्य अनुपात चालू वर्ष तथा आधार-वर्ष की कीमत का प्रतिशत अनुपात है। इसमें सभी वस्तुओं को शामिल नहीं किया जाता अपितु केवल उन्हीं वस्तुओं का न्यादर्श लिया जाता है जो समग्र (Variance) की विशिष्टता को दर्शाते हैं।
स्थिर आधार के मूल्य को 100 मानकर निकाला गया प्रचलित वर्ष का प्रतिशत ही मूल्यानुपात कहलाता है। अतः
${ p }_{ 01 }=\cfrac { { p }_{ 1 } }{ { p }_{ 0 } } \times 100$
यहाँ, P₀₁= मूल्य अनुपात
P₁ = वर्तमान वर्ष की कीमत
P₀= आधार-वर्ष की कीमत
निम्नलिखित सूत्र की सहायता से वर्तमान वर्ष का कीमत सूचकांक ज्ञात किया जा सकता है-
${ p }_{ 01 }=\cfrac { \Sigma (\cfrac { { p }_{ 1 } }{ { p }_{ 2 } } \times 100) }{ N }$
यहाँ, R x 100 = मूल्य अनुपात
N = वस्तुओं की संख्या
P₁ = चालू वर्ष के मूल्य
P₀= आधार-वर्ष के मूल्य
उदाहरण
1.निम्नांकित आँकड़ों की सहायता से सरल मूल्यानुपात माध्य विधि द्वारा 2011 को आधार-वर्ष मानते हुए 2015 के लिए मूल्य सूचकांक ज्ञात कीजिए

प्रश्न 4.
भारित सूचकांक से क्या आशय है? भारित सूचकांक के निर्माण की विधियों को उदाहरण की सहायता से समझाइए।
उत्तर

भारित सूचकांक का अर्थ

भारित सूचकांक वे सूचकांक हैं जिनमें श्रृंखला के विभिन्न मदों को उनके सापेक्षिक महत्त्व के आधार पर विभिन्न भार दिए जाते हैं। इसलिए भारित सूचकांक विभिन्न वस्तुओं की कीमतों का भारित औसत है। उदाहरण-मानी एक उपभोक्ता खाद्यान्नों पर कपड़े की तुलना में तीन गुणा अधिक व्यय करता है तो कपड़े को 1 व खाद्यान्नों को 3 भार दिया जाएगा।

भारित सूचकांक के निर्माण की विधियाँ

भारित सूचकांक के निर्माण की दो विधियाँ हैं
1. भारित औसत मूल्य अनुपात माध्य विधि
2. भारित समूही विधि ।

1. भारित औसत मूल्य अनुपात माध्य विधि— इस विधि द्वारा भारित सूचकांक को ज्ञात करने के लिए, विभिन्न वस्तुओं के मूल्य अनुपातों को उनके भार से गुणा करके गुणनफल के योग को भार के योग से भाग दे दिया जाता है। वस्तुओं को भार उनकी मात्रा के आधार पर दिया जाता है। सूत्र रूप में,
${ p }_{ 01 }=\cfrac { \Sigma RW }{ \Sigma W }$

यहाँ,
P₀₁ = आधार-वर्ष के मूल्यों के आधार पर वर्तमान वर्ष के मूल्यों का सूचकांक
w = भार
R = मूल्य अनुपात

उदाहरण 1. निम्नलिखित आँकड़ों की सहायता से मूल्य अनुपात विधि से 2011 को आधार-वर्ष मानकर 2016 का भारित सूचकांक ज्ञात करेंवस्तुएँ

2. भारित समूही विधि— इस विधि में विभिन्न वस्तुओं को उनकी खरीदी हुई मात्राओं के आधार पर भार प्रदान किया जाता है। विभिन्न विद्वानों ने सूचकांकों का निर्माण करने के लिए भार देने की अलग-अलग विधियों का वर्णन किया है। कुछ प्रमुख विधियाँ निम्नलिखित हैं|
(i) लास्पीयर की विधि (Laspeyre’s Method)-लास्पीयर के आधार-वर्ष की मात्रा (q₀) के आधार पर भार प्रदान किए हैं। सूत्रानुसार,
${ p }_{ 01 }=\cfrac { { \Sigma }p_{ 1 }{ q }_{ 0 } }{ { \Sigma p }_{ 0}{ q }_{ 0 } } \times 100$

(ii) पाश्चे की विधि (Paasche’s Method)- पाश्चे ने चालू वर्ष की मात्रा (q₁) के आधार पर भार प्रदान किए हैं। सूत्रानुसार,
${ p }_{ 01 }=\cfrac { { \Sigma }p_{ 1 }{ q }_{ 1 } }{ { \Sigma p }_{ 0}{ q }_{ 1 } } \times 100$

(iii) फिशर की विधि (Fisher’s Method)- फिशर ने आधार-वर्ष तथा चालू वर्ष दोनों की मात्राओं (q₀ व q₁) के आधार पर भार प्रदान किए हैं। सूत्रानुसार,
p₀₁ $\sqrt { \cfrac { { \Sigma p }_{ 1 }{ q }_{ 0 } }{ \Sigma { p }_{ 0 }{ q }_{ 0 } } \times \cfrac { { \Sigma { p }_{ 1 } }{ q }_{ 1 } }{ \Sigma { p }_{ 0 }{ q }_{ 1 } } } \times 100$

उदाहरण-2011 को आधार-वर्ष मानते हुए निम्नांकित आँकड़ों के कीमत सूचकांक वर्ष 2016 ज्ञात कीजिए-

प्रश्न 5.
उपभोक्ता मूल्य सूचकांक अथवा निर्वाह व्यय सूचकांक से क्या आशय है? इसके निर्माण की विधि उदाहरण की सहायता से समझाइए।
उत्तर
उपभोक्ता मूल्य सूचकांक अथवा निर्वाह व्यय सूचकांक का अर्थ उपभोक्ता मूल्य सूचकांक वह सूचकांक है जो विशिष्ट वर्ग के उपभोक्ताओं द्वारा उपभोग की जाने वाली वस्तुओं तथा सेवाओं की कीमतों में आधार-वर्ष की तुलना में चालू वर्ष में होने वाले परिवर्तन को मापता है। इनका निर्माण विभिन्न स्थानों में रहने वाले उपभोकॅता वर्गों पर फुटकर मूल्यों में होने वाले औसत परिवर्तनों के प्रभावों को मापने के लिए किया जाता है। चूंकि ये किसी वर्ग विशेष के लोगों की निर्वाह लागत में होने वाले परिवर्तन की दिशा तथा मात्रा को प्रकट करते हैं, इसलिए इन्हें निर्वाह व्यय सूचकांक कहा जाता है। भारत में मुख्यत: निम्नलिखित समूहों के लिए उपभोक्ता मूल्य सूचकांक बनाए जाते हैं

औद्योगिक श्रमिक,
शहरी गैर-शारीरिक कर्मचारी तथा
कृषि श्रमिक

जीवन-निर्वाह व्यय सूचकांकों की रचना

जीवन-निर्वाह व्यय सूचकांकों की रचना में निम्नलिखित प्रमुख कार्य करने पड़ते हैं

1. सजातीय वर्ग का चुनाव- सर्वप्रथम यह निश्चित किया जाता है कि सूचकांक किस विशेष वर्ग के लिए बनाए जाते हैं। वर्ग सजातीय होना चाहिए। सजातीय वर्ग का चुनाव मुख्यत: निम्नलिखित आधारों पर किया जाता है-

आय की समानता,
पेशे की समानता,
स्थान की समानता।

2. वस्तुओं का चुनाव- विभिन्न वर्गों के लोग विभिन्न प्रकार की वस्तुओं का प्रयोग करते हैं। अत:
जीवन-निर्वाह व्यय सूचकांक बनाने के लिए वस्तुएँ वही होनी चाहिए, जिनका उपभोग उस वर्ग के लोग करते हैं, जिनके लिए जीवन-निर्वाह व्यय सूचकांक बनाना है। वस्तुओं को मुख्यत: निम्नलिखित वर्गों में बाँट लेते हैं

खाद्य-पदार्थ,
वस्त्र,
ईंधन तथा प्रकाश,
मकान किराया,
अन्य।

3. मूल्य उद्धरण– प्रायः चुनी हुई वस्तुओं के फुटकर मूल्य प्राप्त करने पड़ते हैं। ये मूल्य उस स्थान के बाजार मूल्य होने चाहिए, जहाँ से वह वर्ग उन वस्तुओं को खरीदता है। चूंकि स्थान-स्थान पर फुटकर मूल्यों में बहुत अंतर होता है; अत; उन्हें उस स्थान की उच्चकोटि की पत्रिकाओं, सरकारी एवं अर्द्ध-सरकारी प्रकाशनों, व्यापार परिषदों अथवा प्रतिष्ठित व्यापारियों की सहायता से प्राप्त करना चाहिए।

4. भारांकन- विभिन्न वस्तुओं को उनके महत्त्व के अनुसार भारांकित करना चाहिए। वास्तव में,सभी वस्तुएँ बराबर महत्त्व की नहीं होतीं। भार निम्नलिखित दो प्रकारों में से किसी एक प्रकार से दिया जा सकता है-
(अ) समूही आय विधि- भार देने की इस रीति की प्रमुख प्रक्रियाएँ निम्नलिखित हैं|

प्रत्येक वस्तु से चालू वर्ष के मूल्य में आधार-वर्ष की मात्रा का गुणा करते हैं।
(p₁ q₀)
प्रत्येक वस्तु के आधार-वर्ष के मूल्य में आधार-वर्ष की मात्रा का गुणा करते हैं।
(p₀ q₀)
दोनों वर्षों के गुणनफलों को अलग-अलग जोड़ लेते हैं।
चालू वर्ष के गुणनफलों के योग में आधार-वर्ष के गुणनफलों के योग का भाग दे देते हैं।
प्राप्त भजनफल में 100 का गुणा कर देते हैं।
सूत्रानुसार,

${ p }_{ 01 }=\cfrac { { \Sigma }p_{ 1 }{ q }_{ 0 } }{ { \Sigma p }_{ 0}{ q }_{ 0 } } \times 100$

उदाहरण
1. प्रदत्त आँकड़ों की सहायता से 2011 को आधार-वर्ष मानकर 2016 के लिए जीवन-निर्वाह व्यय सूचकांक (Cost of Living Indexed Number) तैयार कीजिए ।
<
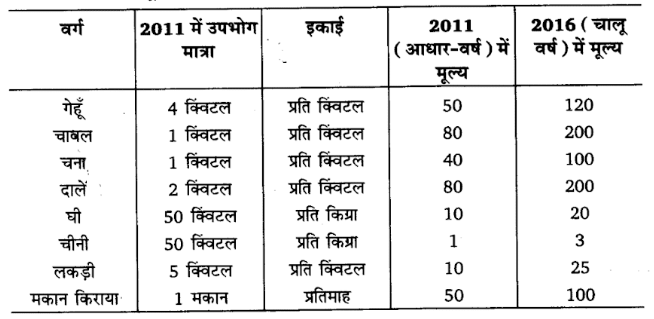
हल

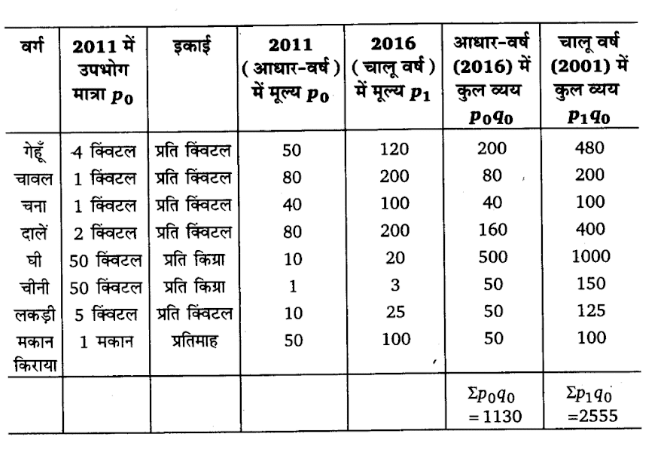
(ब) पारिवारिक बजट या भारित मूल्यानुपात विधि-इस विधि के अनुसार भार देने की प्रक्रिया निम्नलिखित है
(i) प्रत्येक वस्तु के आधार- वर्ष के मूल्य और आधार-वर्ष में उपभोग की गई मात्रा का गुणा करते हैं।
$(\cfrac { { p }_{ 1 } }{ { p }_{ 0 } } \times 100)$
(ii) प्रत्येक वस्तु के आधार-वर्ष के मूल्य और आधार-वर्ष में उपभोग की गई मात्रा का गुणा करते हैं।
(p₀ q₀)
(iii) प्रत्येक मूल्यानुपात को उसके भार से गुणा करते हैं। (RW)।
(iv) इन गुणनफलों का योग कर लेते हैं (ΣRW)।
(v) भारों का योग निकाल लेते हैं (Σw)।
(vi) गुणनफलों के योग में भारों के योग का भाग दे देते हैं।
$(\cfrac { \Sigma RW }{ \Sigma W } )$
प्राप्त भजनफल सूचकांक होता है। सूत्र रूप में,
Index No. $\cfrac { \Sigma RW }{ \Sigma W }$

उदाहरण
2. निम्नलिखित आँकड़ों की सहायता से 2011 को आधार-वर्ष मानकर 2015 और 2016 के लिए जीवन-निर्वाह व्यय सूचकांक तैयार कीजिए

प्रश्न 6.
औद्योगिक उत्पादन का सूचकांक क्या है? इसकी निर्माण विधि समझाइए।
उत्तर-

औद्योगिक उत्पादन का सूचकांक का अर्थ

औद्योगिक उत्पादन का सूचकांक एक देश में किसी आधार-वर्ष की तुलना में चालू वर्ष में औद्योगिक उत्पादन की मात्रा में होने वाली वृद्धि या कमी का माप करता है। इनकी सहायता से हम औद्योगिक उत्पादन की मात्रा में होने वाले परिवर्तनों को मापते हैं, मूल्यों में होने वाले परिवर्तनों को नहीं।

औद्योगिक उत्पादन के सूचकांक की रचना

औद्योगिक उत्पादन के सूचकांक की रचना निम्नलिखित चरणों में की जाती है
1. उद्योगों को समान्यतया तीन वर्गों में बाँट लिया जाता है
(i) खनन,
(ii) विनिर्माण तथा
(iii) विद्युत।
2. उत्पादन संबंधी आँकड़े मासिक, त्रैमासिक या वार्षिक आधार पर एकत्र कर लिए जाते हैं।
3. विभिन्न वर्गों को उपयुक्त भार दिया जाता है। भारत में वर्तमान में इस प्रकार भार दिए गए हैं
(i) खनन = 10.47;
(ii) विनिर्माण = 79.36 तथा
(iii) विद्युत = 10.17
4. निम्नांकित सूत्र का प्रयोग किया जाता है-
$IP=\left[ \cfrac { \Sigma (\cfrac { { q }_{ 1 } }{ { q }_{ 2 } } )W }{ \Sigma w } \right]$
यहाँ, IP = औद्योगिक उत्पादन का सूचकांक |
q₁ = चालू वर्ष में उत्पादन का स्तर ।
q₀= आधार-वर्ष में उत्पादन का स्तर
W = भार।
उदाहरण-निम्नलिखित आँकड़ों की सहायता से औद्योगिक उत्पादन का सूचकांक ज्ञात कीजिए

हल

UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 8 Index Numbers (सूचकांक)

Leave a Reply Cancel reply