UP Board Solutions for Class 11 Geography: Practical Work in Geography Chapter 2 Map Scale (मानचित्र मापनी)

पाठ्य-पुस्तक के प्रश्नोत्तर

प्रश्न 1. नीचे दिए गए चार विकल्पों में से सही विकल्प चुनें
(1) निम्नलिखित में से कौन-सी विधि मापनी की सार्वत्रिक विधि है? |
(क) साधारण प्रकथन
(ख) निरूपक भिन्न
(ग) आलेखी विधि।
(घ) इनमें से कोई नहीं
उत्तर-(ख) निरूपक भिन्न। |

(ii) मानचित्र की दूरी को मापनी में किस रूप में जाना जाता है?
(क) अंश ।
(ख) हर
(ग) मापनी का प्रकथन ।
(घ) निरूपक भिन्न
उत्तर-(क) अंश।

(iii) मापनी में अंश व्यक्त करता है
(क) धरातल की दूरी
(ख) मानचित्र पर दूरी
(ग) दोनों दूरियाँ ।
(घ) इनमें से कोई नहीं
उत्तर-(ख) मानचित्र पर दूरी।।

प्रश्न 2. निम्नलिखित प्रश्नों के उत्तर लगभग 30 शब्दों में दें,
(i) मापक की दो विभिन्न प्रणालियाँ कौन-कौन सी हैं?
उत्तर-मापक की दो विभिन्न प्रणालियाँ निम्नलिखित हैं–
1. मेट्रिक प्रणाली तथा 2. अंग्रेजी प्रणाली।

(ii) मेट्रिक एवं अंग्रेजी प्रणाली में मापनी के एक-एक उदाहरण दें।
उत्तर-उदाहरण-1 किमी = 1,000 मीटर, 1 मीटर = 100 सेमी आदि मापक की मेट्रिक प्रणाली कहलाती है; जबकि 1 मील = 8 फर्लोग, 1 फर्लाग = 220 यार्ड (गज) आदि मापक की अंग्रेजी प्रणाली है।

(iii) निरूपक भिन्न विधि को सार्वत्रिक विधि क्यों कहा जाता है?
उत्तर-निरूपक भिन्न विधि को सार्वत्रिक विधि इसलिए कहा जाता है क्योंकि इस भिन्न के लिए किसी भी प्रकार की इकाई नहीं लिखी होती है। इस भिन्न का अंश सदैव 1 इकाई होता है, जिसे किसी भी देश में वहाँ प्रचलित मापक प्रणाली के आधार पर पढ़ा जाता है। जैसे-1 सेमी = 1 इंच आदि। |

(iv) आलेखी विधि के मुख्य उपयोग क्या हैं?
उत्तर-आलेखी विधि में मानचित्र की दूरी के लिए धरातल की दूरी दी गई होती है। इसके माध्यम से दो स्थानों की दूरी आसानी से ज्ञात की जा सकती है। इस विधि को मुख्य उपयोग यह भी है कि यह मानचित्र के छोटा या बड़ा करने पर भी उसी अनुपात में छोटी या बड़ी हो जाती है। अतः मानचित्र छोटा या बड़ा किए जाने पर मापक को सरलता से जाना जा सकता है।

प्रश्न 3. निम्नलिखित मापनी के प्रकथन को निरूपक भिन्न में बदलें
(i) 5 सेण्टीमीटर, 10 किलोमीटर को व्यक्त करता है।
उत्तर-5 सेण्टीमीटर व्यक्त करता है = 10 किलोमीटर
1 सेण्टीमीटर व्यक्त करेगा = $\frac { 10 }{ 5 }$ = 2 किलोमीटर

(ii) 2 इंच के द्वारा 4 मील व्यक्त होता है।
उत्तर-प्रश्न संख्या (i) के उत्तर में अपनाई गई विधि के आधार पर
2 इंच व्यक्त करता है = 4 मील
1 इंच व्यक्त करेगा = $\frac { 4 }{ 2 }$ = 2 मील
अतः 1 इंच = 2 मील
नि० भि० = $\frac { 1 }{ 2\times 63,360 } =\frac { 1 }{ 1,26,720 }$

(iii) 1 इंच के द्वारा 1 गज व्यक्त होता है।
उत्तर-1 इंच व्यक्त करता है = 1 गज
अतः नि० भि० = $\frac { 1 }{ 1\times 36 } =\frac { 1 }{ 36 }$

(iv) 1 सेण्टीमीटर 100 मीटर को व्यक्त करता है।
उत्तर-1 सेण्टीमीटर व्यक्त करता है = 100 मीटर
अतः नि० भि० = $\frac { 1 }{ 1\times 100 } =\frac { 1 }{ 10,000 }$

प्रश्न 4. निरूपक भिन्न को कोष्ठक में दी गई माप-प्रणाली के अनुसार मापनी के प्रकथन में परिवर्तित करें :
(i) 1:1,00,000 (किलोमीटर में)
उत्तर-1 सेमी व्यक्त करता है 1 किलोमीटर को।

(ii) 1: 31,680 (फर्लाग में)
उत्तर-1 इंच व्यक्त करता है 4 फर्लाग को।
(क्योंकि 1 मील = 8 फर्लंग या 1 मील = 63,360 इंच तथा 1 फर्लाग =7,920 इंच; अत: यदि 31,680 को 7,920 से भाग दिया जाता है तो =4 फर्लाग आता है।)

(iii) 1:1,26,720 (मील में)
उत्तर-1 इंच व्यक्त करता है =2 मील को।
(1,26,720 ÷ 63,360 = 2 मील)। |

(iv) 1:50,000 (मीटर में)
उत्तर-1 सेमी व्यक्त करता है = 500 मीटर को।
(50,000 ÷ 100 सेमी = 500 मीटर)।

प्रश्न 5. 1 : 50,000 मापक पर एक आलेखी मापनी की रचना कीजिए जिसमें किलोमीटर एवं मीटर पढ़े जा सकें।
उत्तर-नि० भि० (R. F.) = 1/50,000
1 सेमी व्यक्त करता है = 50,000 किमी।
15 सेमी व्यक्त करेगा = $\frac { 50,000\times 15 }{ 1,00,000 } =\frac { 15 }{ 2 }$ = 7.5 किमी
7.5 किमी अपूर्ण संख्या है; अत: इसे पूर्णांक संख्या 8 मान लेना चाहिए।
7.5 किमी व्यक्त होता है = 15 सेमी के द्वारा
8 किमी व्यक्त होगा = $\frac { 8\times 15 }{ 7.5 }$ = 16 सेमी
अतः 16 सेमी लम्बी रेखा द्वारा 8 किमी की दूरी पढ़ी जाएगी, जिसे निम्नांकित रेखाचित्र द्वारा प्रदर्शित किया जा सकता है

परीक्षोपयोगी प्रश्नोत्तर

प्रश्न 1. मापक का महत्त्व एवं प्रकार बताइए तथा मानचित्र पर मापक प्रकट करने की विधियों का वर्णन कीजिए।
उत्तर-मापक का महत्त्व

मापक के माध्यम से छोटे क्षेत्रों को बड़े आकार में तथा बड़े क्षेत्रों को छोटे आकार में मानचित्रों के | द्वारा प्रदर्शित किया जा सकता है।
मापक द्वारा किसी भी मानचित्र में दो स्थानों (बिन्दुओं) के मध्य धरातल की वास्तविक दूरी ज्ञात | की जा सकती है।
मापक के माध्यम से एक मानचित्रकार अपने उद्देश्य के अनुसार किसी भी क्षेत्र का छोटा या बड़ा मानचित्र तैयार कर सकता है।

मापक के प्रकार ।

साधारण रूप से मानचित्रों में दो प्रकार के मापक प्रयोग में लाए जाते हैं-
1. दीर्घ मापक मानचित्र-इन मापकों में धरातल की छोटी दूरियों को मानचित्र पर बड़ी माप से प्रदर्शित किया जाता है; जैसे-5 सेमी = 1 किमी या 10″ = 1 मील।।

2. लघु मापक मानचित्र-इन मापकों में धरातल की विशालतम दूरियों को मानचित्र में लघुतम दूरी | से प्रकट किया जाता है; जैसे-1 सेमी = 1,000 किमी या 1″ = 100 मील। लघु मापकों का चुनाव विशाल क्षेत्रों के मानचित्र बनाने के लिए किया जाता है।

मानचित्र पर मापक प्रकट करने की विधियाँ

मापक अभिव्यक्त करने की निम्नलिखित तीन विधियाँ हैं

(I) कथनात्मक विधि
मापक प्रकट करने की यह सरलतम विधि है। इस विधि में मापक को शब्दों द्वारा संक्षेप में व्यक्त किया जा सकता है। यह विधि विभिन्न देशों में प्रचलित माप की इकाई के अनुरूप व्यक्त की जाती है।

उदाहरण के लिए-1 सेमी = 5 किमी, 1″ = 10 मील आदि। इस विधि में दोनों दूरियाँ अलग-अलग । इकाइयों में प्रदर्शित की जाती हैं।

(II) प्रदर्शक भिन्न विधि
इस विधि में मापक का प्रदर्शन एक भिन्न द्वारा किया जाता है। भिन्न का अंश सदैव एक रहता है जो मानचित्र की दूरी प्रकट करता है तथा हर उसी इकाई में क्षेत्र की वास्तविक दूरी को प्रकट करता है। इसे अनुपात को माप की विभिन्न इकाइयों में सरलता से परिवर्तित किया जा सकता है। यद्यपि इस विधि में एक इकाई के द्वारा अनेक इकाइयों का प्रतिनिधित्व किया जाता है; अत: इसे प्रतिनिधि भिन्न या निरूपक भिन्न (R. F.) कहते हैं; जैसे
प्र० भि० = $\\ \frac { 1 }{ 2,000 }$ में मानचित्र की 1 इकाई धारातल की 2,000 इकाइयों का प्रतिनिधित्व कर रही है।

मापक प्रकट करने की इस विधि को भिन्नात्मक या R. F. विधि भी कहते हैं।

मापक परिवर्तन
उदाहरण 1-5 सेमी = 12.5 मीटर को प्र० भि० में बदलो।

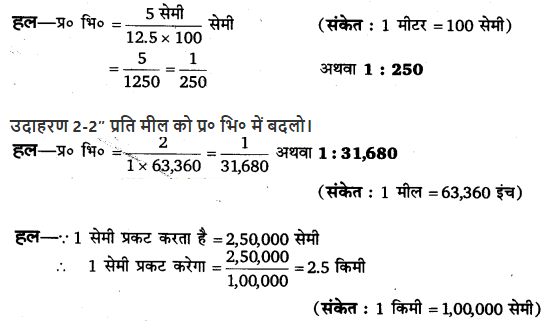
कथुनात्मक मापक 1 सेमी =2.5 किमी।

प्रदर्शक भिन्न विधि का महत्त्व-यह विधि मापक प्रदर्शित करने की अन्तर्राष्ट्रीय विधि है, क्योंकि इस विधि का अन्तर्राष्ट्रीय जगत में उपयोग किया जाता है। इस विधि को विश्व के प्रत्येक राष्ट्र में समझा जा सकता है, क्योंकि इनमें माप की कोई भी इकाई अंकित नहीं होती वरन् यह केवल भिन्नात्मक अनुपात होता है। इस अनुपात को प्रत्येक राष्ट्र अपनी माप की इकाई में बदलकर पढ़ सकती है। इससे मापक की सभी देशों में सार्थकता बनी रहती है।

(III) रेखात्मक विधि
इस विधि में मापक की दूरियाँ एक निश्चित रेखा द्वारा प्रदर्शित की जाती हैं। इस रेखा को समान भागों एवं उपविभागों में बाँट लिया जाता है तथा उस पर विभिन्न माप की दूरियाँ अंकित कर दी जाती हैं। इस मापक विधि के द्वारा बिना किसी गणना किए हुए ही वास्तविक दूरी ज्ञात की जा सकती है। मानचित्र को फोटो द्वारा घटाने या बढ़ाने पर भी रेखात्मक मापनी शुद्ध रहती है, क्योंकि मापनी भी मानचित्र के साथ उसी अनुपात में घट या बढ़ जाती है।

रैखिक मापक बनाने में ध्यान रखने योग्य सावधानियाँ ।

रेखा की लम्बाई मापन के अनुसार प्राय: 6″ या 15 सेमी अधिक सुविधाजनक रहती है।
रेखा को सावधानी से सुविधानुसार समान भागों एवं उपविभागों में विधिवत् विभक्त करना चाहिए।
रेखा का विभाजन पूर्णांक संख्या में ही किया जाना चाहिए।
रेखा की मोटाई प्रत्येक स्थान पर एकसमान होनी चाहिए।
बाईं ओर के उपांश को लघु इकाई में दिखाने के लिए प्रयुक्त करना चाहिए तथा एकान्तर भाग को छाया से रँग देना चाहिए। इसी प्रकार दाईं ओर के समान भागों पर मापे की इकाई अंकित कर देनी चाहिए तथा एकान्तर भाग को छाया से रँग देना चाहिए।
रेखा को समान भागों में विभाजित करने के लिए ज्यामितीय विधियों का प्रयोग करना चाहिए।
रेखा के मुख्य भागों एवं बाईं ओर के उपांशों पर माप की इकाई अंकित कर देनी चाहिए।
मापक के ऊपर लगभग मध्य में प्र० भि० अंकित कर देनी चाहिए।

रेखा विभाजन की विधि-दी हुई रेखा के एक सिरे पर न्यूनकोण बनाइए। न्यूनकोण वाली रेखा को परकार में ली गई किसी भी उचित दूरी से उतने ही सम भागों में विभक्त कीजिए जितने भागों में रेखा को बाँटना है। कोण वाली रेखा के अन्तिम भाग को सरल रेखा के अन्तिम भाग से मिला दीजिए। शेष भागों पर समकोण गुनिया की सहायता से, इसी रेखा के सामान्तर रेखाएँ खींचिए। समानान्तर रेखाएँ सरल रेखा को अपेक्षित समान भागों में बाँट देंगी। (देखिए चित्र 2.1)।

रैखिक मापक के प्रकार
रैखिक मापक के निम्नलिखित प्रकार होते हैं-
1. साधारण मापक-यह सबसे सरल मापक है। इस मापक में दो इकाइयाँ एक साथ प्रदर्शित की जाती हैं; जैसे–मील एवं फर्लाग, गज एवं फुट, किमी एवं हेक्टोमीटर तथा डेकामीटर एवं मीटर आदि। इस मापक में इकाई के दसवें भाग तक को सरलता से पढ़ा जा सकता है। सभी मानचित्रों पर यह मापक बनाया जा सकता है।

2. तुलनात्मक मापक-तुलनात्मक मापक में एक साथ दो या दो से अधिक इकाइयों के साधारण मापक एक ही प्रदर्शक भिन्न पर प्रकट किए जाते हैं तथा इनकी पारस्परिक तुलना की जाती है। प्रत्येक इकाई को प्रदर्शित करने के लिए अलग-अलग मापकों की रचना की जाती है तथा उन्हें एक साथ इस प्रकार रखा जाता है कि सभी मापकों का शून्य एक सीध में रहे। इस मापक में प्रायः मील एवं किमी, गज एवं मीटर, जरीब एवं कदम आदि इकाइयों की तुलना के लिए एक साथ मापक बनाए जा सकते हैं। दो इकाइयों की तुलना के लिए मापक प्रदर्शन की सर्वोत्तम विधि है।

3. कर्णवत मापक-कर्णवत मापक में उपांश को समान भागों में विभक्त करने के लिए आयत के विकर्ण खींचे जाते हैं तथा कर्ण के सहारे-सहारे दूरियाँ प्रकट की जाती हैं; अत: इसे विकर्ण . मापक या कर्णवत मापक कहते हैं। एक साथ तीन इकाइयों अथवा इकाई के सौवें भाग तक के प्रदर्शन के लिए कर्णवत मापक का प्रयोग किया जाता है।

साधारण मापक की रचना

उदाहरण 1-किसी मानचित्र पर दो नगरों के बीच की दूरी को 12 सेमी से प्रकट किया गया है, जबकि उनकी वास्तविक दूरी 420 किमी है। मापक की प्र० भि० ज्ञात कीजिए तथा किमी का साधारण मापक बनाइए।
हल-प्र० भि० = $\frac { 12 }{ 420\times 100000 } =\frac { 1 }{ 3500000 }$ या 1: 35,00,000

मापक की रचना के लिए गणना-
∵1 सेमी प्रकट करता है = 35,00,000 सेमी
∵15 सेमी प्रकट करेंगे = $\\ \frac { 35,00,000\times 15 }{ 1,00,000 }$ किमी = 525 किमी
चूँकि 525 किमी की निकटतम पूर्णांक संख्या 500 है; अत: 500 किमी की दूरी प्रदर्शित करने के लिए रेखा की लम्बाई की गणना निम्नलिखित प्रकार से होगी
∵525 किमी प्रदर्शित होते हैं = 15 सेमी की रेखा द्वारा ।
∵1 किमी प्रदर्शित होगा = $\\ \frac { 15 }{ 525 }$ सेमी की रेखा द्वारा
500 किमी प्रदर्शित होंगे = $\\ \frac { 15 }{ 525 }$ x 500 सेमी की रेखा द्वारा
= $\\ \frac { 100 }{ 7 }$ = 14.28 सेमी की रेखा द्वारा

रचना-14.28 या 14.3 सेमी की रेखा खींचकर उसे 5 समान भागों में विभाजित कीजिए। प्रत्येक भाग 100 किमी की दूरी प्रकट करेगा, पुनः बाएँ उपांश को 10 बराबर भागों में बाँटिए। प्रत्येक उपांश 10 किमी की दूरी प्रकट करेगा (देखें चित्र 2.2)।

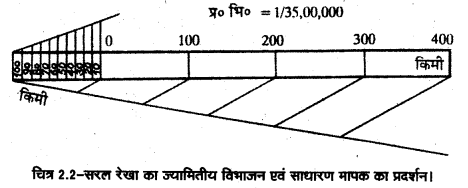
चित्र 2.2-सरल रेखा का ज्यामितीय विभाजन एवं साधारण मापक का प्रदर्शन।

उदाहरण 2- $\\ \frac { 1 }{ 200 }$ की प्र० भि० पर मीटर तथा डेसीमीटर प्रदर्शित करने के लिए एक साधारण मापक बनाइए।
हल-1 सेमी प्रकट करता है =200 सेमी
15 सेमी प्रकट करेंगे = $\\ \frac { 200\times 15 }{ 100 }$ = 30 मीटर
अतः 15 सेमी की रेखा 30 मीटर प्रकट करेगी।

रचना-15 सेमी एक रेखा खींचकर उसे 6 समान भागों में विभाजित कीजिए। प्रत्येक भाग 5 मीटर की दूरी प्रकट करेगा। पुनः बाएँ उपांश को 5 बराबर भागों में बाँटिए। प्रत्येक भाग 10 डेसीमीटर की दूरी प्रकट करेगा (देखें चित्र 2.3)।

चित्र 2.3: साधारण मापक।

उदाहरण 3-एक आलेखी मापनी की रचना कीजिए जिसकी मापनी का प्रकथन 1 मील = 1 इंच है और जिसे मील एवं फर्लाग में पढ़ा जा सके। (पा० पु० पृ० सं० 20; प्र० 2)
हल-नोट: मील या फर्लाग में आलेखी मापक बनाने के लिए प्रायः 6 इंच की लम्बाई ली जाती है।

गणना : नि० भि० (R.F.) 1 इंच = 1 मील या 1/63,360 |
1 इंच व्यक्त करता हैं = 1 मील को ।
6 इंच व्यक्त करेगा = 6 मील को।
अत: 6 इंच लम्बी एक सीधी रेखा खीचें और उसे 6 बराबर भागों में विभाजित करें। प्रत्येक भाग 1 मील को दर्शाएगा। अब बाएँ भाग को चार बराबर भागों में विभाजित करें (1 मील = 8 फर्लाग)। प्रत्येक भाग 2 फर्लंग को प्रदर्शित करेगा (देखिए चित्र 2.4)।

चित्र 2.4

उदाहरण 4-एक आलेखी मापनी बनाएँ जिसमें दिया गया निरूपक भिन्न 1: 50,000 है तथा दूरियों को मील एवं फर्लाग में व्यक्त करें। (पा० पु० पृ० सं० 21; प्र० 3)
हल-गणना–नि० भि० (R.F.) 1 : 50,000
1 इंच व्यक्त करता है = 50,000 इंच
6 इंच व्यक्त करेगा = $\\ \frac { 6\times 50000 }{ 63360 }$ = 4.73 मील
4.73 मील अपूर्ण संख्या को 5 पूर्ण संख्या अर्थात् 5 मील मान लिया जाना चाहिए; अतः रेखा की लम्बाई ज्ञात करें
6 इंच की रेखा द्वारा 4.75 मील व्यक्त किया जाता है।
इसलिए 6 x 5 + 4.73 की रेखा के द्वारा 5 मील व्यक्त किया जाएगा।
अत: 6.34 इंच लम्बाई की रेखा पर 5 मील की दूरी प्रदर्शित की जाएगी।

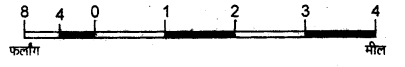
चित्र 2.5

मौखिक परीक्षा के लिए प्रश्नोत्तर

प्रश्न 1. मापक से आप क्या समझते हैं?
उत्तर-“मापक, मानचित्र पर दो स्थानों के बीच की दूरी एवं धरातल पर उन्हीं दोनों स्थानों के बीच की वास्तविक दूरी के मध्य का अनुपात है, जिसे मानचित्र पर प्रदर्शित किया जाता है।”

प्रश्न 2. मापकं प्रकट करने की कौन-कौन सी विधियाँ हैं?
उत्तर-मापक प्रकट करने की निम्नलिखित तीन विधियाँ हैं

कथनात्मक विधि,
प्रदर्शक भिन्न विधि तथा
रेखात्मक विधि।

प्रश्न 3. प्रदर्शक भिन्न क्या है?
उत्तर-“मापक को भिन्न द्वारा प्रकट करने वाली इकाई को प्रदर्शक भिन्न कहते हैं; जैसे – $\\ \frac { 1 }{ 500 }$ या $\\ \frac { 1 }{ 100000 }$ – आदि।” इसमें अंश से मानचित्र की दूरी तथा हर से धरातल की वास्तविक दूरी प्रकट की जाती 1,00,000 है। इस भिन्न का अंश सदैव 1 रहता है। इसे प्र० भि० या नि० भि० (R.F.) भी कहते हैं।

प्रश्न 4. प्रदर्शक भिन्न ज्ञात करने का सूत्र क्या है?
उत्तर-प्रदर्शक भिन्न ज्ञात करने का सूत्र निम्नलिखित है

प्रश्न 5. रेखात्मक मापक में रेखा की लम्बाई कितनी होनी चाहिए?
उत्तर-रेखात्मक मापक में रेखा की लम्बाई 6 इंच अथवा 15 सेमी उपयुक्त रहती है।

प्रश्न 6. रैखिक मापक कितने प्रकार के होते हैं?
उत्तर-रैखिक मापक चार प्रकार के होते हैं।

प्रश्न 7. कर्णवत मापक क्या है?
उतर-लघुतम दूरियाँ प्रकट करने के लिए कर्णवत मापक बनाया जाता है। इसमें एक साथ माप की तीन इकाइयाँ प्रकट की जाती हैं अर्थात् माप इकाई के सौवें भाग तक पढ़ा जा सकता है। कर्णवत मापक में कोई भी दूरी दशमलव के दो अंकों तक मापी जा सकती है। इस मापक में उपांश पर बनाए गए आयतों के विकर्ण बनाए जाते हैं जिसके सहारे तीसरी दूरी प्रकट की जाती है।

प्रश्न 8. साधारण मापक तथा विकर्ण मापक में क्या अन्तर है?
उत्तर–प्रथम, साधारण मापक में एक साथ माप की केवल दो इकाइयाँ ही प्रकट की जा सकती हैं, जबकि विकर्ण मापक में नाप की तीन इकाइयाँ एक साथ प्रदर्शित की जा सकती हैं। द्वितीय, साधारण मापक में इकाई के दसवें भाग तक ही प्रकट किया जा सकता है, जबकि विकर्ण मापक में इकाई के सौवें भाग तक की सूक्ष्म दूरी पढ़ी जा सकती है।

प्रश्न 9. मापक से क्या लाभ हैं?
उत्तर–मापक से निम्नलिखित लाभ हैं—

मापक द्वारा छोटे क्षेत्रों को बड़े तथा बड़े क्षेत्रों को छोटे आकार में दर्शाया जा सकता है।
मापक द्वारा मानचित्र पर किन्हीं भी दो स्थानों के मध्य की वास्तविक धरातलीय दूरी ज्ञात की जा सकती है।

प्रश्न 10. मापनी बनाने की आवश्यकता क्यों होती है?
उत्तर-मापनी द्वारा बहुत बड़े क्षेत्रों को छोटा या छोटे क्षेत्रों को बड़े आकार में प्रदर्शित किया जा सकता है, जो अन्यथा सम्भव नहीं है। इसके द्वारा मानचित्र पर प्रदर्शित क्षेत्र से वास्तविक क्षेत्रफल ज्ञात किया जा सकता

प्रश्न 11. भारतवर्ष में कथनात्मक विधि का प्रयोग प्रायः किस प्रकार के मानचित्र में किया जाता है?
उत्तर-भूसम्पत्ति मानचित्रों एवं भवनों के प्लानों में प्रायः इस विधि का प्रयोग किया जाता है।

प्रश्न 12. रेखात्मक मापनी की क्या विशेषता है?
उत्तर-रेखात्मक मापनी वाले मानचित्र को किसी भी आकार में मुद्रित करने पर मुद्रित मानचित्र की मापनी शुद्ध बनी रहती है, क्योंकि जिस अनुपात में मानचित्र का आकार बदलता है, उसी अनुपात में मापनी की लम्बाई भी बदल जाती है।

प्रश्न 13. प्र० भि० विधि की क्या उपयोगिता है?
उत्तर-इस विधि के मापक का अन्तर्राष्ट्रीय महत्त्व है, क्योंकि इस पर किसी भी देश में प्रचलित इकाई को पढ़ा जा सकता है।

प्रश्न 14. मापक के दो प्रकार बताइए।
उत्तर-1. लघु मापक तथा 2. व्यापक या दीर्घ मापक।

प्रश्न 15. रेखात्मक मापक के मुख्य प्रकार कौन-से हैं?
उत्तर-रेखात्मक मापक के मुख्य प्रकार निम्नलिखित हैं—

साधारण मापक,
तुलनात्मक मापक,
कर्णवत मापक तथा
वर्नियर मापक।।

We hope the UP Board Solutions for Class 11 Geography: Practical Work in Geography Chapter 2 Map Scale (मानचित्र मापनी) help you.

UP Board Solutions for Class 11 Geography: Practical Work in Geography Chapter 2 Map Scale (मानचित्र मापनी)

Leave a Reply Cancel reply