UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations (क्रमचय और संचयं)

प्रश्नावली 7.1

प्रश्न 1.
अंक 1, 2, 3, 4 और 5 से कितनी 3 अंकीय संख्याएँ बनाई जा सकती हैं, यदि
(i) अंकों की पुनरावृत्ति की अनुमति हो।
(ii) अंकों की पुनरावृत्ति की अनुमति नहीं हो।
हल:
3 अंकीय संख्या में 3 स्थान होते हैं : इकाई, दहाई और सैकड़ा।
(i) इकाई का स्थान 5 तरीकों से भरा जा सकता है क्योंकि 1, 2, 3, 4, 5 में से कोई भी एक अंक लिया जा सकता है।
दहाई का स्थान भी 5 तरीकों से भरा जा सकता है क्योंकि पुनरावृत्ति की अनुमति है।
1, 2, 3, 4, 5 में से कोई भी अंक लिया जा सकता है।
इसी प्रकार सैकड़े का स्थान भी 5 तरीकों से भरा जा सकता है।
3 अंकीय संख्याओं की संख्या = 5 x 5 x 5 = 125.

(ii) इकाई का स्थान 1, 2, 3, 4, 5 में से कोई-से एक अंक को लेकर 5 तरीकों से भरा जा सकता है।
दहाई का स्थान 4 तरीकों से भरा जा सकता है क्योंकि एक अंक पहले ही चयनित कर लिया गया। पुनरावृत्ति की अनुमति नहीं है।
सैकड़े का स्थान 3 तरीकों से भरा जा सकता है क्योंकि 2 अंक पहले ही चयनित कर लिए गए हैं।
3 अंकीय संख्याओं की संख्या = 5 x 4 x 3 = 60.

प्रश्न 2.
अंकः1, 2, 3, 4, 5, 6 से कितनी 3 अंकीय सम संख्याएँ बनाई जा सकती हैं, यदि अंकों की पुनरावृत्ति की जा सकेती है?
हल:
इकाई का स्थान 2, 4, 6 में से एक को लेकर 3 तरीकों से भरा जा सकता है।
क्योंकि पुनरावृत्ति की जा सकती है, दहाई का स्थान 6 तरीकों से भरा जा सकता है।
इसी प्रकार सैकड़े का स्थान भी 6 तरीकों से ही भरा जा सकता है।
3 अंकीय संख्याओं की संख्या = 6 x 6 x 3 = 108.

प्रश्न 3.
अंग्रेजी वर्णमाला के प्रथम 10 अक्षरों से कितने 4 अक्षरों के कोड बनाए जा सकते हैं, यदि किसी भी अक्षर की पुनरावृत्ति नहीं की जा सकती?
हल:
4 अक्षरों वाले कोड में 4 स्थान हैं। प्रत्येक अक्षर के लिए एक स्थान चाहिए।
पहले स्थान को 10 तरीकों से, दूसरे स्थान को 9 तरीकों से, तीसरे स्थान को 8 तरीकों से और चौथे स्थान को 7 तरीकों से भर सकते हैं क्योंकि पुनरावृत्ति की अनुमति नहीं है।
एक अक्षर दुबारा नहीं लिखा जा सकता।
चार अक्षर वाले कोडों की संख्या = 10 x 9 x 8 x 7 = 5040.

प्रश्न 4.
0 से 9 तक के अंकों का प्रयोग करके कितने 5 अंकीय टेलीफोन नम्बर बनाए जा सकते हैं, यदि प्रत्येक नम्बर 67 से आरम्भ होता है और कोई अंक एक बार से अधिक नहीं आता है?
हल:
पांच अंकीय नम्बर में 5 स्थान हैं जिसमें पहले और दूसरे को I और II से निरूपित किया गया है। I और II स्थान पर 6 और 7 को रखा गया है।
शेष 8 अंकों में से एक-एक अंक लेकर I, IV और V स्थान को भरना है। स्थान III को 8 तरीकों से, स्थान IV को 7 तरीकों से तथा स्थान V को 6 तरीकों से भर सकते है।
5 अंकीय टेलीफोन नम्बरों की संख्या = 8 x 7 x 6 = 336 .

प्रश्न 5.
एक सिक्का तीन बार उछाला जाता है और परिणाम अंकित कर लिए जाते हैं। परिणामों की संभव संख्या क्या है?
हल:
एक बार सिक्का उछालने से दो में से एक भाग ऊपर आता है अर्थात T या H जबकि H चित्त और T पट को निरूपित करते हैं।
एक बार सिक्का उछालने से दो परिणाम होते हैं।
तीन बार सिक्का उछालने से 2 x 2 x 2 = 8 परिणाम होंगे।
ये परिणाम इस प्रकार है :
TTT, TTH, THT, HTT, HHT, HTH, THH, HHH

प्रश्न 6.
भिन्न-भिन्न रंगों के 5 झंडे दिए हुए हैं। इससे कितने विभिन्न संकेत बनाए जा सकते हैं, यदि प्रत्येक संकेत में 2 झंडों, एक के नीचे दूसरे के प्रयोग की आवश्यक पड़ती है?
हल:
झंडे के ऊपर का स्थान भरने के 5 तरीके हैं। एक झंडा प्रयोग होने के बाद 4 झंडे रह जाते हैं। नीचे का दूसरा स्थान 4 तरीकों से भरा जा सकता है।
कुल संकेतों की संख्या = 5 x 4 = 20.

प्रश्नावली 7.2

प्रश्न 1.
मान निकालिए:
(i) 8!
(ii) 4! – 3!
हल:
(i) 8! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40320.
(ii) 4! – 3! = 4 x 3 x 2 x 1 – 3 x 2 x 1 = 24 – 6 = 18.

प्रश्न 2.
क्या 3! + 4! = 7!
हल:
बायाँ पक्ष = 3! + 4! = 3! + 4! = 3 x 2 x 1 + 4 x 3 x 2 x 1 = 6 + 24 = 30
दायाँ पक्ष = 7! = 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5040
अत: 3! + 4! ≠ 7!

UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.2 3

UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.2 4

UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.2 5

प्रश्नावली 7.3

प्रश्न 1.
1 से 9 तक के अंकों को प्रयोग करके कितनी 3 अंकीय संख्याएं बनाई जा सकती हैं, यदि किसी भी अंक को दोहराया नहीं गया है?
हल:
3 अंकीय संख्या में तीन स्थान होते हैं: इकाई, दहाई और सैकड़ा।
इकाई के स्थान को 9 तरीकों से, दहाई के स्थान को 8 तरीकों से और सैकड़े के स्थान को 7 तरीकों से भरा जा सकता है।
3 अंकीय संख्याओं की संख्या = 9 x 8 x 7 = 504.

प्रश्न 2.
किसी भी अंक को दोहराए बिना कितनी 4 अंकीय संख्याएँ होती हैं?
हल:
0 से 9 तक कुल 10 अंक हैं। 10 में से 4 अंक लेकर संख्याओं की संख्या = 10 ${ P }_{ 4 }$ = 10 x 9 x 8 x 7 = 5640
इनमें वे संख्याएं सम्मिलित हैं जिनमें हजार के स्थान पर 0 है।
0 को हजार के स्थान पर रखने पर और शेष स्थानों पर कोई तीन अंक रखने पर कुल संख्याओं की संख्या
= 9 ${ P }_{ 3 }$ = 9 x 8 x 7 = 504
चार अंकीय संख्याओं की संख्या = 5040 – 504 = 4536.

प्रश्न 3.
अंक 1, 2, 3, 4, 6, 7 को प्रयुक्त करने से कितनी 3 अंकीय सम संख्याएँ बनाई जा सकती हैं, यदि कोई भी अंक दोहराया नहीं गया है?
हल:
2, 4, 6 में से किसी एक को इकाई के स्थान पर रखने से सम संख्या बनती है।
इकाई का स्थान 3 तरीकों से भरा जा सकता है।
दहाई के स्थान को 5 तरीकों से और सैकड़े के स्थान को 4 तरीकों से भरा जा सकता है।
3 अंकीय सम संख्याओं की संख्या = 3 x 5 x 4 = 60.

प्रश्न 4.
अंक 1, 2, 3, 4, 5 के उपयोग द्वारा कितनी 4 अंकीय संख्याएँ बनाई जा सकती हैं। यदि कोई भी अंक दोहराया नहीं गया है? इनमें से कितनी सम संख्याएँ होंगी?
हल:
(i) 5 में से 4 अंक लेकर संख्याओं की संख्या = 5 ${ P }_{ 4 }$ = 5 x 4 x 3 x 2 = 120
(ii) इकाई के स्थान पर 2 या 4 रखने से संख्या सम बनती है।
इस प्रकार इकाई का स्थान 2 तरीकों से, दहाई का स्थान 4 तरीकों से, सैकड़े का स्थान 3 तरीकों से और हजार का स्थान 2 तरीकों से भरा जा सकता है।
4 अंकीय सम संख्याओं की संख्या = 2 x 4 x 3 x 2 = 48.

प्रश्न 5.
8 व्यक्तियों की समिति में, हम कितने प्रकार से एक अध्यक्ष और एक उपाध्यक्ष चुन सकते हैं, यह मानते हुए कि एक व्यक्ति एक से अधिक पद पर नहीं रह सकता है?
हल:
8 व्यक्तियों में से एक को अध्यक्ष चुनने के तरीके = 8
अध्यक्ष चुनने के बाद 7 व्यक्तियों में से एक उपाध्यक्ष चुना जाना है।
उपाध्यक्ष चुनने के तरीके = 7
एक अध्यक्ष और एक उपाध्यक्ष को 8 x 7 = 56 तरीकों से चुना जा सकता है।

UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.3 6

UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.3 7

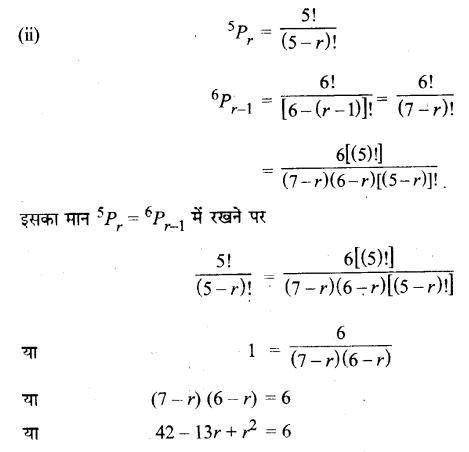
प्रश्न 8.
EQUATION शब्द के अक्षरों में से प्रत्येक को तथ्यतः केवल एक बार उपयोग करके कितने अर्थपूर्ण या अर्थहीन शब्द बन सकते हैं?
हल:
शब्द EQUATION में कुल 8 अक्षर हैं।
इन अक्षरों से बनने वाले शब्दों ( जो अर्थपूर्ण या अर्थहीन हैं) की संख्या = $\frac { 8! }{ \left( 8-8 \right) ! }$ = 8!
= 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40320.

प्रश्न 9.
MONDAY शब्द के अक्षरों से कितने अर्थपूर्ण या अर्थहीन शब्द बन सकते हैं, यह मानते हुए कि किसी भी अक्षर की पुनरावृत्ति नहीं की जाती है,
(i) एक समय में 4 अक्षर लिए जाते हैं?
(ii) एक समय में सभी अक्षर लिए जाते हैं?
(iii) सभी अक्षरों का प्रयोग किया जाता है, किन्तु प्रथम अक्षर एक स्वर है?
हल:
(i) MONDAY शब्द में कुल 6 अक्षर हैं।
6 अक्षरों में से 4 अक्षर एक समय पर लेकर कुल शब्दों की संख्या = 6 ${ P }_{ 4 }$ = 6 x 5 x 4 x 3 = 360
जबकि शब्द अर्थपूर्ण या अर्थहीन हो सकते हैं।
(ii) सभी अक्षरों को एक साथ लेकर शब्दों की संख्या = 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720.
(iii) पहले स्थान पर A या O रखना है। यह दो तरीकों से हो सकता है।
शेष 5 स्थान 5! = 120 तरीकों से भरे जा सकते हैं।
उन शब्दों की संख्या जो स्वर से प्रारम्भ होते हैं = 2 x 120 = 240.

प्रश्न 10.
MISSISSIPPIशब्द के अक्षरों से बने भिन्न-भिन्न क्रमचयों में से कितनों में चारों I एक साथ नहीं आते हैं?
हुल:
शब्द MISSISSIPPI में कुल 11 अक्षर हैं जिसमें M, एक बार; I चार बार; S चार बार, तथा P दो बार प्रयुक्त हो रहे हैं।
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.3 10

प्रश्न 11.
PERMUTATIONS शब्द के अक्षरों को कितने तरीकों से व्यवस्थित किया जा सकता है, यदि
(i) चयनित शब्द का प्रारंभ P से तथा अंत S से होता है।
(ii) चयनित शब्द में सभी स्वर एक साथ हैं।
(iii) चयनित शब्द में P तथा S के मध्य सदैव 4 अक्षर हों?
हल:
PERMUTATIONS शब्द में कुल 12 अक्षर हैं जिनमें T – 2 है, शेष सब भिन्न हैं।
(i) P और 9 के स्थान स्थिर कर दिए गए हैं।
शेष अ६ से बने शब्दों की संख्या = $\frac { 10! }{ 2! }$ = 1814400.

(ii) सभी स्वरों को एक साथ कर दिया गया है।
(EUAIO)PRMTTNS जिनमें 2T हैं।
उन शब्दों की संख्या जब स्वर एक साथ है।
= $\frac { 8! }{ 2! }$ x 5!
= $\frac { 40320 x 120 }{ 2 }$
= 2419200.

(iii) P तथा 5 के बीच चार अक्षर होने चाहिए।
मान लीजिए 12 अक्षरों के स्थानों का नाम 1, 2, 3, …… 12 रख दिया है।
1 2 3 4 5 6 7 8 9 10 11 12
इस प्रकार P को स्थान 1, 2, 3, 4, 5, 6, 7 पर रखा जा सकता है तो S को स्थान 6, 7, 8, 9, 10, 11, 12 पर रखा जा सकता है।
P और S को 7 स्थानों पर रखा जा सकता है।
इसी प्रकार S और P को 7 स्थानों पर रखा जा सकता है।
P और S या S और P को 7 + 7 = 14 तरीकों से रखा जा सकता
शेष $\frac { 10! }{ 2! }$ अक्षरों को 10 तरीकों से व्यवस्थित किया जा सकता है।
उन शब्दों की संख्या जब P और S के बीच में 4 अक्षर हों
= $\frac { 10! }{ 2! }$ x 14 = 10! x 7 = 25401600.

प्रश्नावली 7.4

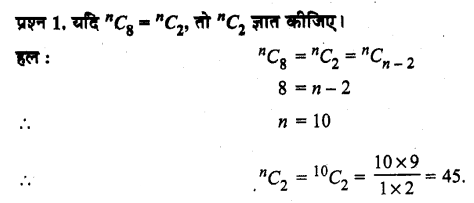
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.4 1

UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.4 2

प्रश्न 3.
किसी वृत्त पर स्थित 21 बिन्दुओं से होकर जाने वाली कितनी जीवाएँ खींची जा सकती हैं?
हल:
21 बिन्दुओं में कोई 2 बिन्दु मिलाने से एक जीवा प्राप्त होती है।
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.4 3

प्रश्न 4.
5 लड़के और 4 लड़कियों में से 3 लड़के और 3 लड़कियों की टीमें बनाने के कितने तरीके हैं?
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.4 4

प्रश्न 5.
6 लाल रंग की, 5 सफेद रंग की और 5 नीले रंग की गेंदों में से 9 गेंदों के चुनने के तरीकों की संख्या ज्ञात कीजिए, यदि प्रत्येक संग्रह में प्रत्येक रंग की 3 गेंदें हैं।
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.4 5

प्रश्न 6.
52 पत्तों की एक गड्डी में से 5 पत्तों को लेकर बनने वाले संचयों की संख्या निर्धारित कीजिए, यदि प्रत्येक संचय में तथ्यतः एक इक्का हो।
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.4 6

प्रश्न 7.
17 खिलाड़ियों में से, जिनमें केवल 5 गेंदबाजी कर सकते हैं, एक क्रिकेट टीम के 11 खिलाड़ियों का चयन कितने प्रकार से किया जा सकता है, यदि प्रत्येक टीम में तथ्यतः 4 गेंदबाज हैं?
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.4 7

प्रश्न 8.
एक थैली में 5 काली तथा 6 लाल गेंदें हैं। 2 काली तथा 3 लाल गेंदों के चयन के तरीकों की संख्या निर्धारित कीजिए।
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.4 8

प्रश्न 9.
9 उपलब्ध पाठ्यक्रमों में से, एक विद्यार्थी 5 पाठ्यक्रमों का चयन कितने प्रकार से कर सकता है, यदि प्रत्येक विद्यार्थी के लिए 2 विशिष्ट पाठ्यक्रम अनिवार्य हैं?
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7.4 9

अध्याय 7 पर विविध प्रश्नावली

प्रश्न 1.
DAUGHTER शब्द के अक्षरों से, कितने अर्थपूर्ण या अर्थहीन शब्दों की रचना की जा सकती है, जबकि प्रत्येक शब्द में 2 स्वर तथा 3 व्यंजन हों?
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 1

प्रश्न 2.
EQUATION शब्द के अक्षरों से कितने, अर्थपूर्ण या अर्थहीन, शब्दों की रचना की जा सकती है, जबकि स्वर तथा व्यंजन एक साथ रहते हैं?
हल:
EQUATION शब्द में कुल 8 अक्षर हैं जिनमें 5 स्वर और 3 व्यंजन हैं।
स्वर अक्षरों का क्रमसंचय = 5! = 5 x 4 x 3 x 2 x 1 = 120
व्यंजन अक्षरों का क्रमसंचय = 3! = 3 x 2 x 1 = 6
स्वरों और अक्षरों को 2 तरीकों से लिखा जा सकता है, पहले स्वर ले या व्यंजन लें।
EQUATION शब्द के अक्षरों से बनने वाले शब्द जब स्वर तथा व्यंजन एक साथ आएँ = 120 x 6 x 2 = 1440.

प्रश्न 3.
9 लड़के और 4 लड़कियों से 7 सदस्यों की एक समिति बनानी है, यह कितने प्रकार से किया सकता है, जबकि समिति में
(i) तथ्यत: 3 लड़कियाँ हैं?
(ii) न्यूनतम 3 लड़कियाँ हैं?
(iii) अधिकतम 3 लड़कियाँ हैं?
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 2

प्रश्न 4.
यदि शब्द EXAMINATION के सभी अक्षरों से बने विभिन्न क्रमचयों को शब्द कोष की तरह सूचीबद्ध किया जाता है, तो E से प्रारम्भ होने वाले प्रथम शब्द से पूर्व कितने शब्द हैं?
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 4

प्रश्न 5.
0, 1, 3, 5, 7 तथा 9 अंकों से, 10 से विभाजित होने वाली और बिना पुनरावृत्ति किए कितनी 6 अंकीय संख्याएँ बनाई जा सकती हैं?
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 5

प्रश्न 6.
अंग्रेजी वर्णमाला में 5 स्वर तथा 21 व्यंजन हैं। इस वर्णमाला में 2 भिन्न स्वरों और 2 भिन्न व्यंजनों वाले कितने शब्दों की रचना की जा सकती है?
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 6

प्रश्न 7.
किसी परीक्षा के एक प्रश्न पत्र में 12 प्रश्न हैं जो क्रमशः 5 तथा 7 प्रश्नों वाले दो खण्डों में विभक्त हैं अर्थात खंड 1 और खण्ड II, एक विद्यार्थी का प्रत्येक खंड से न्यूनतम 3 प्रश्नों का चयन करते हुए कुल 8 प्रश्नों को हल करना है। एक विद्यार्थी कितने प्रकार से प्रश्नों का चयन कर सकता है ?
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 7

प्रश्न 8.
52 पत्तों की एक गड्डी में से 5 पत्तों के संचय की संख्या निर्धारित कीजिए, यदि 5 पत्तों के प्रत्येक चयन (संचय) में तथ्यतः एक बादशाह है।
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 8

प्रश्न 9.
5 पुरुषों और 4 महिलाओं को एक पंक्ति में इस प्रकार बैठाया जाता है कि महिलाएँ सम स्थानों पर बैठती हैं। इस प्रकार कितने विन्यास संभव हैं ?
हल:
4 महिलाओं का 4 सम स्थानों पर बैठाने के विन्यास = 4! = 24
5 पुरुषों को 5 विषम स्थानों पर बैठाना के तरीके = 5! = 120
4 महिलाओं को सम स्थानों पर और 5 पुरुषों को विषम स्थानों पर बैठाने के विन्यास = 4! x 5! = 24 x 120 = 2880.

प्रश्न 10.
25 विद्यार्थियों की एक कक्षा से 10 का चयन एक भ्रमण दल के लिए किया जाता है। तीन विद्यार्थी ऐसे हैं, जिन्होंने यह निर्णय लिया है कि या तो वे तीनों दल में शामिल होंगे या उनमें से कोई भी दल में शामिल नहीं होगा। भ्रमण दल का चयन कितने प्रकार से किया जा सकता है?
हल:
25 विद्यार्थियों में से 10 विद्यार्थियों को भ्रमण दल में शामिल करना है। परन्तु 10 विद्यार्थियों में से 3 ऎसे हैं
(i) जब तीनों भ्रमण दल में शामिल होते हैं या (ii) तीनों नहीं होते है।
(i) जब तीनों विद्यार्थी टीम में शामिल होते हैं तो भ्रमण दल का चयन करने के तरीके = 22 ${ C }_{ 7 }$
(ii) जब तीनों विद्यार्थी भ्रमण दल में शामिल नहीं होते हैं तो चयन करने के तरीके = 22 ${ C }_{ 10 }$
दोनो दशाओं में भ्रमण दल का चयन करने के तरीके = 22 ${ C }_{ 7 }$ + 22 ${ C }_{ 10 }$

प्रश्न 11.
ASSASSINATION शब्द के अक्षरों के कितने विन्यास बनाए जा सकते हैं जबकि सभी sएक साथ रहें ?
हुल:
ASSASSINATION में कुल 13 अक्षर हैं जिसमें A तीन बार, S चार बार, I दो बार तथा N दो बार प्रयुक्त हो रहे हैं।
4 – S को एक साथ रहना है। अतः उसे एक अक्षर मान लिया। इस प्रकार इसमें 10 अक्षर रह गए जिसमें 3 – A, 2 – 1 और 2 – N समान हैं।
इस शब्द के अक्षरों का विन्यास जब S एक साथ रहते हो
UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations 11

We hope the UP Board Solutions for Class 11 Maths Chapter 7 Permutation and Combinations (क्रमचय और संचयं) help you.

UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations (क्रमचय और संचयं)

Leave a Reply Cancel reply