UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane (समतल में गति)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1:
निम्नलिखित भौतिक राशियों में से बताइए कि कौन-सी सदिश हैं और कौन-सी अदिश-आयतन, द्रव्यमान, चाल, त्वरण, घनत्व, मोल संख्या, वेग, कोणीय आवृत्ति, विस्थापन, कोणीय वेग।
उत्तर:
सदिश राशियाँ: त्वरण, वेग, विस्थापन तथा कोणीय वेग।
अदिश राशियाँ: आयतन, द्रव्यमान, चाल, घनत्व, मोल-संख्या तथा कोणीय आवृत्ति।

प्रश्न 2:
निम्नांकित सूची में से दो अदिश राशियों को छाँटिए
बल, कोणीय संवेग, कार्य, धारा, रैखिक संवेग, विद्युत क्षेत्र, औसत वेग, चुम्बकीय आघूर्ण, आपेक्षिक वेग।
उत्तर:
दो अदिश राशियाँ कार्य तथा धारा हैं।

प्रश्न 3:
निम्नलिखित सूची में से एकमात्र सदिश राशि को छाँटिए
ताप, दाब, आवेग, समय, शक्ति, पूरी पथ-लम्बाई, ऊर्जा, गुरुत्वीय विभव, घर्षण गुणांक, आवेश।
उत्तर:
दी गई राशियों में एकमात्र सदिश राशि आवेग है।

प्रश्न 4:
कारण सहित बताइए कि अदिश तथा सदिश राशियों के साथ क्या निम्नलिखित बीजगणितीय संक्रियाएँ अर्थपूर्ण हैं
(a) दो अदिशों को जोड़ना,
(b) एक ही विमाओं के एक सदिश व एक अदिश को जोड़ना,
(c) एक सदिश को एक अदिश से गुणा करना,
(d) दो अदिशों का गुणन,
(e) दो सदिशों को जोड़ना,
(f) एक सदिश के घटक को उसी सदिश से जोड़ना?
उत्तर:
(a) नहीं, दो अदिशों को जोड़ना केवल तभी अर्थपूर्ण हो सकता है, जबकि दोनों एक ही भौतिक राशि को प्रदर्शित करते हों।
(b) नहीं, सदिश को केवल सदिश के साथ तैथा अदिश को केवल अदिश के साथ ही जोड़ा जा सकता है।,
(c) अर्थपूर्ण है, एक सदिश को एक अदिश से गुणा करने पर एक नया सदिश प्राप्त होता है, जिसका परिमाण सदिश व अदिश के परिमाण के गुणन के बराबर होता है तथा दिशा अपरिवर्तित रहती है।
(d) अर्थपूर्ण है, दो अदिशों के गुणन से प्राप्त नए अदिश का परिमाण दिए गए अदिशों के परिमाण के । गुणन के बराबर होता है।
(e) नहीं, केवल तभी अर्थपूर्ण होगा जबकि दोनों एक ही भौतिक राशि को प्रदर्शित करते हों।
(f) चूँकि किसी सदिश का घटक एक सदिश होता है जो मूल सदिश के समान भौतिक राशि को निरूपित करता है (जैसे-बल का घटक भी एक बल ही होता है); अत: दोनों को जोड़ना अर्थपूर्ण है।

प्रश्न 5:
निम्नलिखित में से प्रत्येक कथन को ध्यानपूर्वक पढिए और कारण सहित बताइए कि यह सत्य है या असत्य
(a) किसी सदिश का परिमाण सदैव एक अदिश होता है।
(b) किसी सदिश का प्रत्येक घटक सदैव अदिश होता है।
(c) किसी कण द्वारा चली गई पथ की कुल लम्बाई सदैव विस्थापन सदिश के परिमाण के बराबर होती है।
(d) किसी कण की औसत चाल (पथ तय करने में लगे समय द्वारा विभाजित कुल पथ-लम्बाई) समय के समान-अन्तराल में कण के औसत वेग के परिमाण से अधिक या उसके बराबर होती है।
(e) उन तीन सदिशों का योग जो एक समतल में नहीं हैं, कभी भी शून्य सदिश नहीं होता।
उत्तर:
(a) सत्य, किसी भी भौतिक राशि का परिमाण एक धनात्मक संख्या है, जिसमें दिशा नहीं होती; अतः यह एक अदिश राशि है।
(b) असत्य, किसी सदिश का प्रत्येक घटक एक सदिश राशि होता है।
(c) असत्य, उदाहरण के लिए यदि कोई व्यक्ति R त्रिज्या के वृत्त की परिधि पर चलते हुए एक चक्कर पूर्ण करता है तो उसके द्वारा तय किए गए पथ की लम्बाई 2π R होगी जबकि विस्थापन का परिमाण शून्य होगा।
(d) सत्य, क्योंकि औसत चाल पूर्ण पथ की लम्बाई पर तथा औसत वेग कुल विस्थापन पर निर्भर करता है। जबकि पूर्ण पथ की लम्बाई सदैव ही विस्थापन के परिमाण से अधिक अथवा बराबर
होती है।
(e) सत्य, शून्य सदिश प्राप्त करने के लिए तीसरा सदिश पहले दो सदिशों के परिणामी के विपरीत दिशा में तथा परिमाण में उसके बराबर होना चाहिए। यह इस दशा में सम्भव नहीं है, चूँकि तीनों सदिश एक समतल में नहीं हैं।

प्रश्न 6:
निम्नलिखित असमिकाओं की ज्यामिति या किसी अन्य विधि द्वारा स्थापना कीजिए
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 1
उत्तर:

प्रश्न 7:
दिया है $\xrightarrow { a }$ + $\xrightarrow { b }$ + $\xrightarrow { c }$ + $\xrightarrow { d }$ = 0 नीचे दिए गए कथनों में से कौन-सा सही है
(a) $\xrightarrow { a }$ , $\xrightarrow { b }$ , $\xrightarrow { c }$ तथा $\xrightarrow { d }$ में से प्रत्येक शून्य सदिश है।
(b) ( $\xrightarrow { a }$ + $\xrightarrow { c }$ ) का परिमाण ( $\xrightarrow { d}$ + $\xrightarrow { d }$ ) के परिमाण के बराबर है।
(c) $\xrightarrow { a }$ का परिमाण $\xrightarrow { b }$ , $\xrightarrow { c }$ तथा $\xrightarrow { d}$ के परिमाणों के योग से कभी-भी अधिक नहीं हो सकता।
(d) यदि $\xrightarrow { a }$ तथा $\xrightarrow { d }$ संरेखीय नहीं हैं तो $\xrightarrow { b }$ + $\xrightarrow { c }$ अवश्य ही $\xrightarrow { a }$ तथा $\xrightarrow { d }$ के समतल में होगा और । यह $\xrightarrow { a }$ तथा $\xrightarrow { d }$ के अनुदिश होगा यदि वे संरेखीय हैं।
उत्तर:
(a) यह कथन सही नहीं है क्योंकि सदिश $\xrightarrow { a }$ , $\xrightarrow { b }$ , $\xrightarrow { c }$ तथा $\xrightarrow { d }$ का योग शून्य है, जिससे यह परिणाम
प्राप्त नहीं होता है कि प्रत्येक शून्य सदिश है। अत: कथन (a) सत्य नहीं है।

प्रश्न 8:
तीन लड़कियाँ 200 in त्रिज्या वाली वृत्तीय बर्फीली सतह पर स्केटिंग कर रही हैं। वे सतह के किनारे के बिन्दु P से स्केटिंग शुरू करती हैं तथा P के व्यासीय विपरीत बिन्दु Qपर विभिन्न पथों से होकर पहुँचती हैं, जैसा कि संलग्न चित्र 4.2 में दिखाया गया है। प्रत्येक लड़की के विस्थापन सदिश का परिमाण कितना है? किस लड़की के लिए यह वास्तव में स्केट किए गए पथ की लम्बाई के बराबर है?
हल:
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 6
दिया है : वृत्तीय पथ की त्रिज्या (R) = 200 m
∵ प्रत्येक लड़की का विस्थापन सदिश = $\xrightarrow { PQ }$
∴ विस्थापन सदिश का परिमाण = व्यास PQ की लम्बाई
= 2R = 2x200m
= 400 m
∵ लड़की B द्वारा तय पथ (PQ) की लम्बाई = 2R = 400m
∴ लड़की B के लिए विस्थापन संदिश का परिमाण वास्तव में स्केट चित्र 4.2 किए गए पथ की लम्बाई के बराबर है।

प्रश्न 9:
कोई साइकिल सवार किसी वृत्तीय पार्क के केन्द्र से चलना शुरू करता है तथा पार्क के किनारे P पर पहुँचता है। पुनः वह पार्क की परिधि के अनुदिश साइकिल चलाता हुआ Qo के रास्ते (जैसा कि चित्र 4.3 में दिखाया गया है) केन्द्र पर वापस आ जाता है। पार्क की त्रिज्या 1 km है। यदि पूरे चक्कर में 10 मिनट लगते हों तो साइकिल सवार का (a) कुल विस्थापन, (b) औसत वेग तथा (c) औसत चाल क्या होगी?
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 7
हल:
(a) दिया है : वृत्तीय पार्क की त्रिज्या = 1km
चूंकि साइकिल सवार केन्द्र० से चलकर पुनः केन्द्र0 पर ही पहुँच जाता है, अतः कुल विस्थापन = 0

प्रश्न 10:
किसी खुले मैदान में कोई मोटर चालक एक ऐसा रास्ता अपनाता है जो प्रत्येक 500m के बाद उसके बाईं ओर 60° के कोण पर मुड़ जाता है। किसी दिए मोड़ से शुरू होकर मोटर चालक का तीसरे, छठे व आठवें मोड़ पर विस्थापन बताइए। प्रत्येक स्थिति में मोटर चालक द्वारा इन मोड़ों पर तय की गई कुल पध-लम्बाई के साथ विस्थापन के परिमाण की तुलना कीजिए।
हल:
मोटर चालक द्वारा अपनाया गया मार्ग एक समषट्भुज ABCDEF आकार का होगा।
(a) माना कि मोटर चालक शीर्ष A से चलना प्रारम्भ करता है।
तो वह शीर्ष D पर तीसरा मोड़ लेगा। प्रश्नानुसार,
AB = BC = CD = DE = EF = FA = 500 m
∴ तीसरे मोड़ पर विस्थापन ,
= AD = 2x AB (समषट्भुज के गुण से)
= 2x 500 m = 1000 m = 1km
जबकि कुल पथ की लम्बाई
= AB+ BC + CD
= (500 + 500 + 500) m
= 1500 m = 1.5 km
∴ विस्थापन : पथ-लम्बाई = 1 km : 1.5 km = 2:3
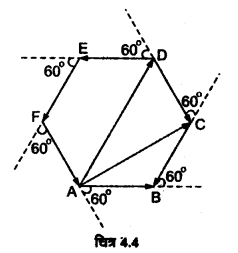
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 9
(b) मोटर चालक छठा मोड़ शीर्ष A पर लेगा अर्थात् इस क्षण मोटर चालक अपने प्रारम्भिक बिन्दु पर पहुँच चुका होगा।
∴ विस्थापन = शून्य।
जबकि कुल पथ-लम्बाई = AB+ BC + CD+DE. + EF + FA
= 6 x AB = 6 x 500m
= 3000 m = 3 km
विस्थापन : पथ-लम्बाई = 0:3km = 0
(c) मोटर चालक आठवाँ मोड़ शीर्ष C पर लेगा।

प्रश्न 11:
कोई यात्री किसी नए शहर में आया है और वह स्टेशन से किसी सीधी सड़क पर स्थित किसी होटल तक जो 10 km दूर है, जाना चाहता है। कोई बेईमान टैक्सी चालक 23 km के चक्करदार रास्ते से उसे ले जाता है और 28 min में होटल में पहुँचता है।
(a) टैक्सी की औसत चाल, और
(b) औसत वेग का परिमाण क्या होगा? क्या वे बराबर हैं।
हल:
दिया है : टैक्सी द्वारा तय कुल दूरी = 23 km,
लगा समय = 28 min
टैक्सी का विस्थापन = स्टेशन से होटल तक सरल रेखीय दूरी
= 10km
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 11

प्रश्न 12:
वर्षा का पानी 30 ms^-1 की चाल से ऊर्ध्वाधर नीचे गिर रहा है। कोई महिला उत्तर सेदक्षिण की ओर 10 ms^-1 की चाल से साइकिल चला रही है। उसे अपना छाता किस दिशा में रखना चाहिए?
हल:

UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 13

प्रश्न 13:
कोई व्यक्ति स्थिर जल में 4.0 km/h की चाल से तैर सकता है। उसे 1.0 km चौड़ी नदी को पार करने में कितना समय लगेगा? यदि नदी 3.0 km/h की स्थिर चाल से बह रही हो और वह नदी के बहाव के लम्ब तैर रहा हो। जब वह नदी के दूसरे किनारे पहुँचता है तो वह नदी के बहाव की ओर कितनी दूर पहुँचेगा?
हल:
∵ तैराक नदी के लम्ब दिशा में तैर रहा है; अतः तैराक का अपना वेग नदी के लम्ब दिशा में कार्य करेगा जब इस दिशा में नदी के अपने वेग का कोई प्रभाव नहीं होगा।
अतः नदी के लम्ब दिशा में नेट वेग = तैराक का अपना वेग
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 14

प्रश्न 14:
किसी बन्दरगाह में 72 km/h की चाल से हवा चल रही है और बन्दरगाह में खड़ी किसी नौका के ऊपर लगा झण्डा N-E दिशा में लहरा रहा है। यदि वह नौका उत्तर की ओर 51 km/h की चाल से गति करना प्रारम्भ कर दे तो नौको पर लगा झण्डा किस दिशा में लहराएगा?
हल:

प्रश्न 15:
किसी लम्बे हॉल की छत 25 m ऊँची है। वह अधिकतम क्षैतिज दूरी कितनी होगी जिसमें 40 ms^-1 की चाल से फेंकी गई कोई गेंद छत से टकराए बिना गुजर जाए?
हल:
यहाँ प्रक्षेप्य वेग u = 40 मी/से, महत्तम ऊँचाई HM = 25 मी

प्रश्न 16:
क्रिकेट का कोई खिलाड़ी किसी गेंद को 100 m की अधिकतम क्षैतिज दूरी तक फेंक सकता है। वह खिलाड़ी उसी गेंद को जमीन से ऊपर कितनी ऊँचाई तक फेंक सकता है?
हल:
यहाँ अधिकतम क्षैतिज परास R_max = 100 मी
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 20

प्रश्न 17:
80 cm लम्बे धागे के एक सिरे पर एक पत्थर बाँधा गया है और इसे किसी एकसमान चाल के साथ किसी क्षैतिज वृत्त में घुमाया जाता है। यदि पत्थर 25 s में 14 चक्कर लगाता है तो पत्थर के त्वरण का परिमाण और उसकी दिशा क्या होगी?
हल:
पत्थर द्वारा अपनाए गए वृत्तीय मार्ग की त्रिज्या R = 80 cm = 0.8 m

प्रश्न 18:
कोई वायुयान 900 kmh^-1 की एकसमान चाल से उड़ रहा है और 1.00 km त्रिज्या का कोई क्षैतिज लूप बनाता है। इसके अभिकेन्द्र त्वरण की गुरुत्वीय त्वरण के साथ तुलना कीजिए।
हल:
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 23

प्रश्न 19:
नीचे दिए गए कथनों को ध्यानपूर्वक पढिए और कारण सहित बताइए कि वे सत्य हैं या असत्य
(a) वृत्तीय गति में किसी कण का नेट त्वरण हमेशा वृत्त की त्रिज्या के अनुदिश केन्द्र की ओर होता है।
(b) किसी बिन्दु पर किसी कण का वेग सदिश सदैव उस बिन्दु पर कण के पथ की स्पर्श रेखा के अनुदिश होता है।
(c) किसी कण को एकसमान वृत्तीय गति में एक चक्र में लिया गया औसत त्वरण सदिश एक शून्य सदिश होता है।
उतर:
(a) असत्य है क्योंकि यह कथन केवल एकसमान वृत्तीय गति के लिए सत्य है।
(b) सत्य है क्योंकि यदि कण की गति में त्वरण, वेग के अनुदिश है तो कण सरल रेखीय पथ पर गति करता है और यदि गति में त्वरण किसी अन्य दिशा में है तो कण वक्र पथ पर गति करता है तथा वेग
की दिशा पथ के स्पर्श रेखीय रहती है।
(c) सत्य है क्योंकि एक अर्द्धचक्र में त्वरण; दूसरे अर्द्धचक्र में त्वरण के ठीक बराबर व विपरीत होता है।

प्रश्न 20:
किसी कण की स्थिति सदिश निम्नलिखित है

समय t सेकण्ड में है तथा सभी गुणकों के मात्रक इस प्रकार से हैं $\xrightarrow { r }$ कि मीटर में व्यक्त हो जाए।
(a) कण का $\xrightarrow { v }$ तथा $\xrightarrow { a }$ निकालिए,
(b) t = 2.0s पर कण के वेग का परिमाण तथा दिशा कितनी होगी?
हल:

प्रश्न 21:
कोई कण t = 0 क्षण पर मूलबिन्दु से 10 $\hat { j }$ ms-1 के वेग से चलना प्रारम्भ करता है।
तथा x-y समतल में एकसमान त्वरण (8.0 $\hat { i }$ +20 $\hat { j }$ ) ms-2 से गति करता है।
(a) किस क्षण कण का x-निर्देशांक 16 m होगा? इसी समय इसका y-निर्देशांक कितना होगा?
(b) इसी क्षण किसी कण की चाल कितनी होगी?
हल:

प्रश्न 22:
$\hat { i }$ तथा $\hat { j }$ क्रमशः x-व y-अक्षों के अनुदिशएकांक सदिश हैं। सदिशों $\hat { i }$ + $\hat { j }$ तथा – $\hat { j }$ का परिमाण तथा दिशाएँ क्या होंगी? सदिशों A = 2 $\hat { i }$ + 3 $\hat { j }$ के $\hat { i }$ + $\hat { j }$ व – $\hat { j }$ की दिशाओं के अनुदिश घटक निकालिए (आप ग्राफी विधि का उपयोग कर सकते हैं)।
हल:
$\hat { i }$ तथा $\hat { j }$ परस्पर लम्ब एकांक सदिश हैं; अर्थात् इनके बीच का कोण θ = 90° है।
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 28

प्रश्न 23:
किसी दिकस्थान पर एक स्वेच्छ गति के लिए निम्नलिखित सम्बन्धों में से कौन-सा सत्य है?
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 30
यहाँ औसत की आशय समयान्तराल t₂ व t₁ से सम्बन्धित भौतिक राशि के औसत मेन से है।
उत्तर:
(a) असत्य,
(b) सत्य,
(c) असत्य,
(d) असत्य,
(e) सत्य।

प्रश्न 24:
निम्नलिखित में से प्रत्येक कथन को ध्यानपूर्वक पढिए तथा कारण एवं उदाहरण सहित बताइए कि क्या यह सत्य है या असत्य अदिश वह राशि है जो
(a) किसी प्रक्रिया में संरक्षित रहती है,
(b) कभी ऋणात्मक नहीं होती,
(c) विमाहीन होती है,
(d) किसी स्थान पर एक बिन्दु से दूसरे बिन्दु के बीच नहीं बदलती,
(e) उन सभी दर्शकों के लिए एक ही मान रखती है चाहे अक्षों से उनके अभिविन्यास भिन्न-भिन्न क्यों न हों?
उत्तर:
(a) असत्य है, क्योंकि किसी अदिश का किसी प्रक्रिया में संरक्षित रहना आवश्यक नहीं है। उदाहरण के लिए, ऊपर की ओर फेंके गए पिण्ड की गतिज ऊर्जा (अदिश राशि) पूरी यात्रा में बदलती रहती है।
(b) असत्य है, क्योंकि अदिश राशि ऋणात्मक, शून्य या धनात्मक कुछ भी मान ग्रहण कर सकती है; जैसे किसी वस्तु का ताप एक अदिश राशि है, जो धनात्मक, शून्य या ऋणात्मक कुछ भी हो सकता है।
(c) असत्य है, उदाहरण के लिए, किसी वस्तु का द्रव्यमान अदिश राशि है परन्तु इसकी विमा (M¹) है।
(d) असत्य है, उदाहरण के लिए ताप एक अदिश राशि है, किसी छड़ में ऊष्मा के एकविमीय प्रवाह में, प्रवाह की दिशा में ताप बदलता जाता है।
(e) सत्य है, क्योंकि अदिश राशि में दिशा नहीं होती; अतः यह प्रत्येक विन्यास में स्थित दर्शक के लिए समान मान रखती है। उदाहरण के लिए, किसी वस्तु के द्रव्यमान का मान प्रत्येक दर्शक के लिए समान होगा।

प्रश्न 25:
कोई वायुयान पृथ्वी से 3400 m की ऊँचाई पर उड़ रहा है। यदि पृथ्वी पर किसी अवलोकन बिन्दु पर वायुयान की 10.0 s की दूरी की स्थितियाँ 30° का कोण बनाती हैं तो वायुयान की चाल क्या होगी?
हल:
माना 10s के अन्तराल पर वायुयान की दो स्थितियाँ क्रमशः P तथा Q हैं जबकि 0 प्रेक्षण बिन्दु है।

अतिरिक्त अभ्यास

प्रश्न 26:
किसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या दिक़स्थान में इसकी कोई स्थिति होती है? क्या यह समय के साथ परिवर्तित हो सकता है? क्या दिकस्थान में भिन्न स्थानों पर दो बराबर सदिशों $\xrightarrow { a }$ व $\xrightarrow { b }$ का समान भौतिक प्रभाव अवश्य पड़ेगा? अपने उत्तर के समर्थन में उदाहरण दीजिए।
उत्तर:
सभी सदिशों की स्थिति नहीं होती। किसी बिन्दु के स्थिति सदिश के समान कुछ सदिशों की स्थिति होती है जबकि वेग सदिश के समान कुछ सदिशों की कोई स्थिति नहीं होती। हाँ, कोई सदिश समय के साथ परिवर्तित हो सकता है, जैसे- गतिमान कण की स्थिति सदिश । आवश्यक नहीं है, उदाहरण के लिए दो अलग-अलग बिन्दुओं पर लगे बराबर बल अलग-अलग आघूर्ण उत्पन्न करेंगे।

प्रश्न 27:
किसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या इसका यह अर्थ है कि कोई राशि जिसका परिमाण व दिशा हो, वह अवश्य ही सदिश होगी? किसी वस्तु के घूर्णन की व्याख्या घूर्णन-अक्ष की दिशा और अक्ष के परितः घूर्णन-कोण द्वारा की जा सकती है। क्या इसका यह अर्थ है कि कोई भी घूर्णन एक सदिश है?
उत्तर:
किसी राशि में परिमाण तथा दिशी होने पर उसका सदिश होना आवश्यक नहीं है। सदिश होने के लिए किसी राशि में परिमाण तथा दिशा के साथ-साथ उसे सदिश नियमों का पालन भी करना चाहिए। उदाहरण के लिए प्रत्येक घूर्णन कोण एक सदिश राशि नहीं हो सकता। केवल सूक्ष्म घूर्णन को ही सदिश राशि माना जा सकता है।

प्रश्न 28:
क्या आप निम्नलिखित्व के साथ कोई संदिश सम्बद्ध कर सकते हैं-
(a) किसी लूप में मोड़ी गई तार की लम्बाई,
(b) किसी समतल क्षेत्र,
(c) किसी गोले के साथ? व्याख्या कीजिए।
उत्तर:
(a) नहीं, क्योंकि वृत्तीय लूप में मोड़े गए तार की कोई निश्चित दिशा नहीं होती।
(b) हाँ, दिए गए समतल पर एक निश्चित अभिलम्ब खींचा जा सकता है; अत: समतल क्षेत्र के साथ एक सदिश सम्बद्ध किया जा सकता है जिसकी दिशा समतल पर अभिलम्ब के अनुदिश हो सकती
(c) नहीं, क्योंकि किसी गोले का आयतन किसी विशेष दिशा के साथ सम्बद्ध नहीं किया जा सकता।

प्रश्न 29:
कोई गोली क्षैतिज से 30° के कोण पर दागी गई है और वह धरातल पर 3:0km दूर गिरती है। इसके प्रक्षेप्य के कोण का समायोजन करके क्या 5.0 km दूर स्थित किसी लक्ष्य का भेद किया जा सकता है? गोली की नालमुखी चाल को नियत तथा वायु के प्रतिरोध को नगण्य मानिए।
हल:
यहाँ प्रक्षेप्य कोण θ₀ = 30°
तथा क्षैतिज परास R = 3.0 किमी
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 32

प्रश्न 30:
कोई लड़ाकू जहाज 1.5 km की ऊँचाई पर 720 km/h की चाल से क्षैतिज दिशा में उड़ रहा है और किसी वायुयान भेदी तोप के ठीक ऊपर से गुजरता है। ऊध्र्वाधर से तोप की नाल का क्या कोण हो जिससे 600 ms^-1 की चाल से दागा गया गोला वायुयान पर वार कर सके। वायुयान के चालक को किस न्यूनतम ऊँचाई पर जहाज को उड़ाना चाहिए जिससे गोली लगने से बच सके। (g = 10 ms^-2)
हल:
लड़ाकू जहाज की ऊँचाई,

प्रश्न 31:
एक साइकिल सवार 27 km/h की चाल से साइकिल चला रहा है। जैसे ही सड़क पर वह 80 m त्रिज्या के वृत्तीय मोड़ पर पहुँचता है, वह ब्रेक लगाता है और अपनी चाल को 0.5 m/s की एकसमान दर से कम कर लेता है। वृत्तीय मोड़ पर साइकिल सवार के नेट त्वरण का परिमाण और उसकी दिशा निकालिए।
हल:

प्रश्न 32:
(a) सिद्ध कीजिए कि किसी प्रक्षेप्य के -अक्ष तथा उसके वेग के बीच के कोण को समय के फलन के रूप में निम्न प्रकार से व्यक्त कर सकते हैं
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 37
उत्तर:
(a) माना कोई प्रक्षेप्य मूलबिन्दु से इस प्रकार फेंका जाता है कि उसके वेग के x-अक्ष तथा y-अक्षों की दिशाओं में वियोजित घटक क्रमश: Vox तथा v0y हैं।
माना t समय पश्चात् प्रक्षेप्य बिन्दु P पर पहुँचता है, जहाँ उसको स्थिति सदिश $\xrightarrow { r }$ (t) है।

UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 74

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न

प्रश्न 1:
मीनार की छत से एक गेंद को किक किया जाता है तो गेंद पर लगने वाले क्षैतिज एवं ऊध्र्वाधर त्वरण का मान होगा
(i) 0 एवं 9.8 मी/से²
(ii) 9.8 मी/से एवं 9.8 मी/से^-2
(iii) 9.8 मी/से^-2 एवं 0
(iv) 9.8 मी/से^-2 एवं 4.9 मी/से ^-2
उत्तर:
(i) 0 एवं 9.8 मी/से²

प्रश्न 2:
प्रक्षेप्य गति के दौरान निम्नलिखित में से कौन-सी राशि संरक्षित रहती है?
(i) यान्त्रिक ऊर्जा
(ii) स्थितिज ऊर्जा
(iii) संवेग
(iv) गतिज ऊर्जा
उत्तर:
(i) यान्त्रिक ऊर्जा

प्रश्न 3:
जब एक वस्तु दो विभिन्न प्रक्षेप्य कोणों पर प्रक्षेपित की जाती है तो उसकी क्षैतिज परास | समान है। यदि h₁ तथा h₂ उसकी संगत महत्तम ऊँचाइयाँ हैं, तो उसकी क्षैतिज परास R तथा h₁व h₂ में सही सम्बन्ध होगा।

उत्तर:

प्रश्न 4:
क्षैतिजत: कुछ ऊँचाई पर जाते हुए एक बम वर्षक विमान को पृथ्वी पर किसी लक्ष्य पर बम मारने के लिए बम तब गिराना चाहिए जब वह
(i) लक्ष्य के ठीक ऊपर है।
(ii) लक्ष्य से आगे निकल जाता है।
(iii) लक्ष्य के पीछे है।
(iv) उपर्युक्त तीनों सही हैं।
उत्तर:
(iii) लक्ष्य के पीछे है।

प्रश्न 5:
प्रक्षेप्य पथ के उच्चतम बिन्दु पर त्वरण का मान होता है।
(i) अधिक
(ii) न्यूनतम
(iii) शून्य
(iv) g के बराबर
उत्तर:
(iv) g के बराबर

प्रश्न 6:
प्रक्षेप्य गति में उच्चतम बिन्दु पर वेग है।
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 41
उत्तर:
(ii) u cosθ

प्रश्न 7:
एक प्रक्षेप्य गतिज ऊर्जा K से प्रक्षेपित किया जाता है। यदि यह अधिकतम परास तक जाए तो इसकी अधिकतम ऊँचाई पर गतिज ऊर्जा होगी
(i) 0.25K
(ii) 0.5K
(iii) 0.75K
(iv) 1.0K
उत्तर:
(ii) 0.5K

प्रश्न 8:
एक प्रक्षेप्य का प्रारम्भिक वेग v = (3 $\hat { i }$ +4 $\hat { j }$ ) मी/से है। महत्तम ऊँचाई पर इसका वेग होगा।
(i) 3 मी/से
(ii) 4 मी/से
(iii) 5 मी/से
(iv) शून्य
उत्तर:
(iii) 5 मी/से

प्रश्न 9:
जब किसी वस्तु को महत्तम परास (maximum range) वाले कोण से फेंका जाता है। तब उसकी गतिज ऊर्जा है। अपने पथ की महत्तम ऊँचाई वाले बिन्दु पर उसकी क्षैतिज गतिज ऊर्जा है।
(i) E
(ii) E/2
(iii) E/3
(iv) शून्य
उत्तर:
(ii) E/2

प्रश्न 10:
30° कोण पर झुके नत समतल के निचले सिरे पर एक कण प्रक्षेपित किया जाता है। क्षैतिज . से किस कोण 80 पर कण प्रक्षेपित किया जाये ताकि वह नत समतल पर अधिकतम परास में किया , प्राप्त कर सके?
(i) 45°
(ii) 53°
(iii) 75°
(iv) 60°
उत्तर:
(iii) 75°

प्रश्न 11:
क्रिकेट का कोई खिलाड़ी किसी गेंद को पृथ्वी पर अधिकतम 100 मीटर क्षैतिज दूरी तक फेंक सकता है। वह खिलाड़ी उसी गेंद को पृथ्वी से ऊपर जिस अधिकतम ऊँचाई तक फेंक सकता है, है।
(i) 100 मीटर
(ii) 50 मीटर
(iii) 25 मीटर
(iv) 15 मीटर
उत्तर:
(ii) 50 मीटर है

प्रश्न 12:
एक प्रक्षेप्य को क्षैतिज परास, उसकी अधिकतम प्राप्त ऊँचाई का चार गुना है। क्षैतिज से इसका प्रक्षेप्य कोण होगा
(i) 30°
(ii) 60°
(iii) 45°
(iv) 90°
उत्तर:
(iii) 45°

प्रश्न 13:
अधिकतम परास के लिए किसी कण का प्रक्षेपण कोण होना चाहिए
(i) क्षैतिज से 0° के कोण पर
(ii) क्षैतिज से 60° के कोण पर
(iii) क्षैतिज से 30°के कोण पर
(iv) क्षैतिज से 450 के कोण पर
उत्तर:
(iv) क्षैतिज से 450 के कोण पर

प्रश्न 14:
एक गेंद किसी मीनार की चोटी से 60° कोण पर (ऊध्र्वाधर से) प्रक्षेपित की जाती है।इसके वेग का ऊर्ध्व घटक
(i) लगातार बढ़ता जायेगा
(ii) लगातार घटता जायेगा
(iii) अपरिवर्तित रहेगा
(iv) पहले घटता है तथा फिर बढ़ता है।
उत्तर:
(iv) पहले घटता है तथा फिर बढ़ता है।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1:
प्रक्षेप्य गति से क्या तात्पर्य है?
उत्तर:
जब किसी पिण्डे को एक प्रारम्भिक वेग से ऊध्र्वाधर दिशा से भिन्न किसी दिशा में फेंका जाता है। तो उस पर गुरुत्वीय त्वरण सदैव ऊर्ध्वाधर नीचे की ओर लगता है तथा पिण्ड ऊध्र्वाधर तल में एक वक्र पथ पर गति करता है। इस गति को प्रक्षेप्य गति कहते हैं।

प्रश्न 2:
प्रक्षेप्य गति किस प्रकार की गति है-एकविमीय अथवा द्विविमीय?
उत्तर:
प्रक्षेप्य गति द्विविमीय गति है।

प्रश्न 3:
क्षैतिज से किसी कोण पर ऊर्ध्वाधर तल में प्रक्षेपित पिण्ड का पथ कैसा होता है?
उत्तर:
परवलयाकार।

प्रश्न 4:
प्रक्षेप्य-पथ किस प्रकार का होता है? क्या यह पथ ऋजुरेखीय हो सकता है?
उत्तर:
प्रक्षेप्य-पथ परवलयाकार होता है। प्रक्षेप्य-पथ ऋजुरेखीय नहीं हो सकता।

प्रश्न 5:
“पृथ्वी से छोड़े गये प्रक्षेप्य का पथ परवलयाकार होता है। प्रक्षेप्य की चाल पथ के उच्चतम बिन्दु पर न्यूनतम होगी।” समझाइए कि यह कथन सत्य है या असत्य।
उत्तर:
यह कथन सत्य है, क्योंकि उच्चतम बिन्दु पर प्रक्षेपण वेग का ऊर्ध्व घटक शून्य हो जाता है तथा क्षैतिज घटक अपरिवर्तित रहता है।

प्रश्न 6:
प्रक्षेपण पथ के किस बिन्दु पर चाल निम्नतम होती है तथा किस बिन्दु पर अधिकतम?
उत्तर:
उच्चतम बिन्दु पर चाल निम्नतम तथा प्रक्षेपण बिन्दु पर चाल अधिकतम होती है।

प्रश्न 7:
प्रक्षेपण पथ के उच्चतम बिन्दु पर प्रक्षेप्य की गति की दिशा क्षैतिज क्यों हो जाती है?
उत्तर:
क्योंकि उच्चतम बिन्दु पर प्रक्षेप्य के वेग का ऊर्ध्व घटक शून्य हो जाता है। इसमें केवल क्षैतिज घटक ही रह जाने के कारण प्रक्षेप्य की गति की दिशा प्रक्षेपण पथ के उच्चतम बिन्दु पर क्षैतिज हो जाती है।

प्रश्न 8:
प्रक्षेप्य-पथ के उच्चतम बिन्दु पर वेग व त्वरण की दिशाओं के बीच कितना कोण होता है?
उत्तर:
90°

प्रश्न 9:
किसी प्रक्षेप्य द्वारा महत्तम ऊँचाई के लिए सूत्र लिखिए।
उत्तर:
H_M = u_0² sin² θ₀/2g, जहाँ u₀ = प्रक्षेपण वेग,
θ₀= प्रक्षेपण कोण तथा g = गुरुत्वीय त्वरण

प्रश्न 10:
प्रक्षेप्य के क्षैतिज परास का व्यंजक लिखिए।
उत्तर:
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 42

प्रश्न 11:
प्रक्षेप्य के उड्डयनकाल (T) की परिभाषा एवं सूत्र लिखिए।
उत्तर:
जितने समय में पिण्ड प्रक्षेपण बिन्दु से उच्चतम बिन्दु तक पहुँचकर अपने परवलय पथ द्वारा प्रक्षेपण-बिन्दु की सीध में नीचे आता है, उसे पिण्ड का उड्डयनकाल कहते हैं।

प्रश्न 12:
वायु के प्रतिरोध का प्रक्षेप्य के उड्डयन काल तुथा परास पर क्या प्रभाव पड़ता है?
उत्तर:
वायु के प्रतिरोध से उड्डयन काल बढ़ जाता है तथा परास घट जाता हैं।

प्रश्न 13:
एक वस्तु को क्षैतिज से θ कोण पर $\xrightarrow { U }$ वेग से प्रक्षेपित किया जाता है। उन दो राशियों के नाम बताइए जो नियत रहती हैं।
उत्तर:
वेग का क्षैतिज घटक = u cos θ तथा ऊर्ध्व दिशा में त्वरण $\xrightarrow { g }$ के नीचे की ओर।

प्रश्न 14:
एक खिलाड़ी गेंद को क्षैतिज से किस झुकाव पर फेंके कि गेंद अधिकतम दूरी तक जाए?
उत्तर:
45°.

लघु उत्तरीय प्रश्न

प्रश्न 1:
एक प्रक्षेप्य (गेंद) पृथ्वी के गुरुत्वीय क्षेत्र में क्षैतिज से θ कोण पर u वेग से फेंका जाता है। प्रक्षेप्य का उड्डयनकाल तथा क्षैतिज परास ज्ञात कीजिए।
उत्तर:
प्रक्षेप्यका उडड्यनकाल:
पिण्ड को प्रक्षेपण बिन्दु O से अधिकतम ऊँचाई के बिन्दु तक जाकर पुनः क्षैतिज के अन्य बिन्दु C तक आने लगे समय को उड्डयन काल कहते हैं। इसे प्राय: T से व्यक्त करते हैं।
माना पिण्ड अपने पथ के उच्चतम बिन्दु P तक पहुँचने में t समय लेता है। P पर पिण्ड का अन्तिम ऊर्ध्वाधर वेग शून्य है। अतः ν_y = 0; गति के प्रथम समीकरण) ν = u+ at में ν= ν_y = 0, u= u_y = = u sin θ0 तथा 4 के स्थान पर (- g) रखकर ‘t’ के मान की गणना कर सकते हैं।

पिण्ड उच्चतम बिन्दु P परे, पहुँचकर अपने परवलयाकार गमन पथ द्वारा नीचे आने लगता है, जितने समय में पिण्ड बिन्दु ० से उच्चतम बिन्दु P तक जाता है उतने ही समय में वह बिन्दु P से C तक लौटता है जो कि बिन्दु 0 की ठीक सीध में है। अतः पिण्ड को उड्डयन काल
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 45
प्रक्षेप्य का क्षैतिज परास:
प्रक्षेप्य अपने उड्डयन काल में जितनी क्षैतिज दूरी तय करता है उसे प्रक्षेप्य की परास कहते हैं। इसे प्राय: R से व्यक्त करते हैं।
चित्र 4.11 से क्षैतिज परास OC=( क्षैतिज वेग) x (उड्डयन काल)
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 46
समीकरण (1) से स्पष्ट है कि अधिकतम क्षैतिज परास के लिए, sin 2θ0 =1 अर्थात् 2θ₀ = 90° अथवा θ₀ = 45°, अतः पिण्डे का अधिकतम परास प्राप्त करने के लिए पिण्ड को 45° पर प्रक्षेपित किया जाना चाहिए। इस दशा में
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 47
यही कारण है कि पृथ्वी पर लम्बी कूद (long jump) करने वाला खिलाड़ी पृथ्वी से 45° के कोण पर उछलता है।
सूत्र (2) में यदि θ₀ के स्थान पर (90°-θ₀) रखें, तब
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 48
इससे स्पष्ट है कि पिण्ड को चाहे θ0 कोण पर प्रक्षेपित करें अथवा (90° – θ₀) कोण पर, दोनों दशाओं में क्षैतिज परास R वही रहती है।

प्रश्न 2:
एक पत्थर पृथ्वी तल से क्षैतिज से 30° कोण पर 49 मी/से के वेग से फेंका जाता है। इसका उड्डयन काल तथा क्षेतिज परास ज्ञात कीजिए।
हल:
दिया है, प्रक्षेप्य कोण θ₀= 30°

प्रश्न 3:
एक प्रक्षेप्य का प्रारम्भिक वेग (3 $\hat { i }$ +4 $\hat { j }$ ) मी/से है। इसकी महत्तम ऊँचाई तथा क्षैतिज परांस ज्ञात कीजिए। (g=10 मी/से²)
हल:
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 50

प्रश्न 4:
एक व्यक्ति 2 किग्रा एवं 3 किग्रा के दो गोले समान वेग से क्षैतिज से समान झुकाव कोण पर फेंकता है। बताइए कौन-सा गोला पृथ्वी पर पहले पहुँचेगा? यदि गोले भिन्न-भिन्न वेगों से फेंके जाएँ तब कौन-सा पहले पहुँचेगा?
उत्तर:
प्रक्षेप्य का उड्डयन काल

सूत्र से स्पष्ट है कि उड्डयन काल प्रक्षेपित पिण्ड के द्रव्यमान पर निर्भर नहीं करता। अतः दोनों गोले पृथ्वी पर एक साथ पहुंचेंगे। उड्डयन काल प्रक्षेपण वेग u0 पर निर्भर करता है तथा T α uo। अत: जिस गोले का प्रक्षेपण वेग कम है, वह पहले पृथ्वी पर पहुँचेगा।

प्रश्न 5:
पृथ्वी के गुरुत्व के अन्तर्गत गति करते हुए किसी प्रक्षेप की महत्तऊँचाई यदि h हो, तो सिद्ध कीजिए कि उसका प्रक्षेपण वेग
[latex]\frac{\sqrt{2 g h}}{\sin \theta}[/latex] होगा, जबकि θ प्रक्षेपण कोण है।
उत्तर:
गति के तृतीय समीकरण से, प्रक्षेप्य की ऊर्ध्वाधर गति के लिए।
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 52

प्रश्न 6:
एक पुल से एक पत्थर क्षैतिज से नीचे की ओर 30° के कोण पर 25 मी/से के वेग से फेंका जाता है। यदि पत्थर 2.5 सेकण्ड में जल से टकराता है तो जल के पृष्ठ से पुल की ऊँचाई ज्ञात कीजिए। पत्थर का क्षैतिज परास भी ज्ञात कीजिए। (g = 98 मी/से²)
हल:
∵ प्रक्षेपण बिन्दु पर प्रक्षेपण के क्षण नीचे की ओर पत्थर का वेग
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 54

प्रश्न 7:
एक पत्थर 10 मी/से के वेग से क्षैतिज के साथ 30° के कोण पर एक मीनार की चोटी से ऊपर की ओर फेंका जाता है। 5-सेकण्ड के उपरान्त वह जमीन से टकराता है। जमीन से मीनार की ऊँचाई और पत्थर के क्षैतिज परास की गणना कीजिए। (g = 10 मी/से²)
हल:
प्रक्षेपण बिन्दु पर प्रक्षेपण के समय पत्थर का वेग = u sinθ
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 55

प्रश्न 8:
एक मीनार की चोटी से एक गेंद क्षैतिज से ऊपर 10 मीटर/सेकण्ड के प्रारम्भिक वेग से ऊध्र्वाधर से 60° का कोण बनाते हुए फेंकी जाती है। वह मीनार के आधार से 10√3 मीटर की दूरी पर पृथ्वी पर टकराती है। मीनार की ऊँचाई ज्ञात कीजिए। (मान लीजिए g = 10 मीटर/सेकण्ड²)।
हल:
गेंद को प्रक्षेप्य कोण θ₀ = 90° – 60° = 30° तथा प्रक्षेप्य वेग u= 10 मीटर/सेकण्ड। प्रक्षेप्य वेग को क्षैतिज तथा ऊर्ध्व घटकों में वियोजित करने पर,
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 56

प्रश्न 9:
एक मीनार की चोटी से एक गेंद को 15 मीटर/सेकण्डनियत क्षैतिज वेग से प्रक्षेपित किया जाता है। 4 सेकण्ड पश्चात गेंद का विस्थापन ज्ञात कीजिए तथा सदिश आरेख भी खींचिए। (g = 10 मीटर/सेकण्ड²)
हल:
दिया है, u_x = 15 मीटर/सेकण्ड, t = 4 सेकण्ड

प्रश्न 10:
प्रक्षेप्य,पथ के परवलयाकार होने के प्रतिबन्ध बताइए।
उत्तर:
प्रक्षेप्य का पथ परवलयाकार होने के प्रतिबन्ध-प्रक्षेप्य का पथ परवलयाकार तभी हो सकता है, जबकि उक्त प्रतिबन्ध सन्तुष्ट हो। इसके लिए निम्नलिखित प्रतिबन्ध आवश्यक हैं
1. प्रक्षेप्य द्वारा प्राप्त ऊँचाई बहुत अधिक नहीं होनी चाहिए अन्यथा ४ को परिमाण बदल जाएगा।
2. प्रक्षेप्य का परास बहुत अधिक नहीं होना चाहिए अन्यथा ४ की दिशा परिवर्तित हो जाएगी।
3. प्रक्षेप्य का प्रारम्भिक वेग कम होना चाहिए जिससे कि वायु का प्रतिरोध नगण्य रहे। उपर्युक्त प्रतिबन्धों के सन्तुष्ट होने पर ही प्रक्षेप्य पथ एक परवलय रहेगा अन्यथा बदल जाएगा।

विस्तृत उत्तरीय प्रश्न

प्रश्न 1:
प्रक्षेप्य गति से क्या तात्पर्य है? दर्शाइए कि प्रक्षेप्य गति में पथ के उच्चतम बिन्दु पर पिण्ड के वेग तथा त्वरण एक-दूसरे के लम्बवत होते हैं।
उत्तर:
प्रक्षेप्य गति- “जब किसी पिण्ड को पृथ्वी के गुरुत्वीय क्षेत्र में, किसी प्रारम्भिक वेग से ऊध्र्वाधर दिशा से भिन्न दिशा में फेंका जाता है तो पिण्ड गुरुत्वीय त्वरण के अन्तर्गत ऊर्ध्वाधर तल में एक वक्र पथ पर गति करता है। पिण्ड़ की इस गति को प्रक्षेप्य गति (Projectile motion) कहते हैं तथा पिण्ड द्वारा तय किए गए पथ को प्रक्षेप्य पथ (trajectory) तथा फेंके गए पिण्ड को प्रक्षेप्य (Projectile) कहते हैं।”

उदाहरण:
छत से फेंकी गई गेंद की गति, हवाई जहाज से गिराए गए बम की गति, तोप से छूटे गोले की गति, भाला फेंक (javelin throw) में भाले की गति, बल्ले से मारने पर गेंद की गति तथा एकसमान ‘ विद्युत क्षेत्र में उसके लम्बवत् प्रवेश करने वाले किसी आवेशित कण की गति आदि प्रक्षेप्य गति के ही उदाहरण हैं।

प्रक्षेप्य का कोणीय प्रक्षेपण:
माना किसी प्रक्षेप्य को प्रारम्भिक वेग u से क्षैतिज से θ कोण पर प्रक्षेपित किया गया है।
प्रक्षेप्य के प्रारम्भिक वेग का घटक (u_x) = u cos θ
तथा ऊध्र्वाधर घटक (u_y) = u sin θ
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 59
यदि वायु के प्रतिरोध को नगण्य मान लिया जाए, तो पिण्ड पर क्षैतिज दिशा में कोई बल नहीं लगेगा। अतः, क्षैतिज दिशा में पिण्ड का त्वरण भी शून्य होगा और इसलिए क्षैतिज दिशा में पिण्ड का वेग अपरिवर्तित रहेगा। इसके विपरीत पिण्ड पर गुरुत्वीय त्वरण ऊध्र्वाधरतः नीचे की ओर क्रिया करेगा।
क्षैतिज दिशा में, a_x = 0 तथा ऊध्र्वाधर दिशा में, a_y =-g
t समय बाद क्षैतिज गति के लिए समीकरण s = ut + $\frac { 1 }{ 2 }$ at² का प्रयोग करने पर तय की गई दूरी,
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 60
इस प्रकार, प्रक्षेप्य गति में वेग का क्षैतिज घटक (u_x = u cos θ) सम्पूर्ण गति में अपरिवर्तित रहता है, जबकि वेग को ऊर्ध्वाधर घटक (u_y = u sin θ) निरन्तर परिवर्तित होता रहता है तथा पथ के उच्चतम बिन्दु पर इसका मान शून्य हो जाता है। अत: उच्चतम बिन्दु पर वेग का मान न्यूनतम ucosθ हो जाता है, जिसकी दिशा, क्षैतिज होती है तथा त्वरण g की दिशा ऊध्र्वाधर दिशा में नीचे की ओर होती है। इस प्रकार पथ के उच्चतम बिन्दु पर वेग तथा त्वरण के बीच का कोण 90° होता है।

प्रश्न 2:
यदि कोई प्रक्षेप्य गुरुत्वीय क्षेत्र में क्षैतिज से θ कोण पर u वेग से प्रक्षेपित किया जाता है, तो सिद्ध कीजिए कि प्रक्षेप्य-पथ एक परवलय होगा।
या
सिद्ध कीजिए कि प्रक्षेप्य-पथ परवलयाकार होता है।
उत्तर:
प्रक्षेप्य का पथ:
माना पृथ्वी तल के किसी बिन्दू O से एक पिण्ड को क्षैतिज से θ कोण पर प्रक्षेप्य वेग u से ऊध्र्वाधर तल में प्रक्षेपित किया जाता है (चित्र 4.15)। माना बिन्दु O मूलबिन्दु है तथा प्रक्षेप्य के ऊर्ध्वाधर समतल में बिन्दु0 से गुजरने वाली क्षैतिज तथा ऊध्र्वाधर रेखाएँ क्रमश: X तथा Y-अक्ष हैं।

प्रारम्भिक प्रक्षेप्य वेग u को क्षैतिज (Ox के अनुदिश) तथा ऊध्र्वाधर (OY के अनुदिश) घटकों में वियोजित करने पर,
क्षैतिज घटक u_x = u cos θ
तथा , ऊध्र्वाधर, घटक u_y = u sinθ
प्रक्षेपित पिण्ड गुरुत्वीय त्वरण g के अन्तर्गत गति करता है। चूंकि g का मान स्थिर है तथा यह सदैव ऊध्र्वाधर दिशा में नीचे की ओर कार्य करता है; अतः पिण्ड के क्षैतिज वेग ॥ पर गुरुत्वीय त्वरण ‘g’ का कोई प्रभाव नहीं पड़ता। माना पिण्ड पर वायु का अवरोध नगण्य है तो पिण्ड का क्षैतिज वेग u_x(= u cos θ) पूरी गति के दौरान अपरिवर्तित रहेगा, परन्तु पिण्ड के वेग का ऊर्ध्व घटक u_y(= u sin θ) का मान गुरुत्वीय त्वरण g के कारण लगातार बदलता रहेगा। इस प्रकार, क्षैतिज दिशा में, प्रारम्भिक वेग u_x = u cos तथा त्वरण a_x = 0
तथा ऊर्ध्वाधर दिशा में, प्रारम्भिक वेग u_y = u sin θ तथा त्वरण a_y= – g
माना t समय में पिण्ड बिन्दु (x, y) पर पहुँच जाता है, तब
t समय में पिण्ड का क्षैतिज विस्थापन = x
तथा ऊध्र्वाधर विस्थापन = y

यह समीकरण y = bx-cx² के स्वरूप को है जो एक परवलय को प्रदर्शित करता है; अतः पृथ्वी के गुरुत्वीय क्षेत्र में प्रक्षेपित पिण्ड का प्रक्षेप्य-पथ परवलयाकार होता है। इस कथन को सर्वप्रथम गैलीलियो ने सिद्ध किया था।

प्रश्न 3:
सिद्ध कीजिए कि एक ही वेगu से क्षैतिज से θ तथा (90° -θ ) कोणों पर किसी प्रक्षेप्य को फेंकने पर प्रक्षेप्य समान परास प्राप्त करता है। यदि इन दो दिशाओं में प्रक्षेप्य के उड्डयन काल क्रमश:TतथाT’ हों तथा प्राप्त महत्तम ऊँचाइयाँ क्रमशः h वh’ हों, तो सिद्ध कीजिए कि
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 64
उत्तर:
एक ही पास के लिए दो प्रक्षेपण कोण–माना कि प्रक्षेप्य θ व (90° – θ) कोणों पर फेंके जाने पर क्रमशः R व R’ परास प्राप्त करता है तब
UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane 65
इससे स्पष्ट है कि गेंद को चाहे से कोण पर प्रक्षेपित करें अथवा (90° – θ) कोण पर, दोनों दशाओं में क्षैतिज परास R का मान वही रहता है।
उदाहरण:
एक खिलाड़ी फुटबॉल को चाहे क्षैतिज से 30° के कोण पर ‘किक’ करे अथवा 90° – 30° = 60° के कोण पर फुटबॉल पृथ्वी पर दोनों स्थितियों में एक ही स्थान पर गिरेगी।

प्रश्न 4:
“किसी ऊँचाई से पृथ्वी के समान्तर प्रक्षेपित पिण्ड का पथ भी परवलयाकार होता है।” सिद्ध कीजिए। पिण्ड के उड्डयन काल तथा क्षैतिज परास का व्यजंक स्थापित कीजिए।
उत्तर:
किसी ऊँचाई से पृथ्वी के समान्तर प्रक्षेपित । पिण्ड का पथ- चित्र 4.16 में पृथ्वी तल से H ऊँचाई पर स्थित कोई बिन्दु O है, जहाँ से कोई पिण्ड (प्रक्षेप्य) क्षैतिज दिशा OX में अर्थात् पृथ्वी के समान्तर प्रारम्भिक वेग 06 से प्रक्षेपित किया गया है। YOY’ बिन्दु O से गुजरती पृथ्वी के लम्बवत् रेखा है। अतः O को मूलबिन्दु मानते हुए प्रारम्भ में अर्थात् किसी क्षण t पर X₀ = 0 तथा y₀ = 0. क्षैतिज दिशा में पिण्ड पर कोई त्वरण कार्य नहीं करता है अर्थात् a_X = 0, इसलिए इस दिशा में प्रक्षेप्य का वेग ν0 नियत रहता है। ऊध्र्वाधरत: नीचे की ओर पिण्ड का त्वरण a_Y = – g.

माना प्रक्षेपित किए जाने के समय पश्चात् अर्थात् क्षण ।
पर पिण्ड प्रक्षेप्य पथ के बिन्दु P पर है जिसके निर्देशांक (x, -y) हैं अर्थात् पिण्ड ने नियत ν0 वेग से T समय में क्षैतिज दूरी X तय की है तथा गुरुत्व के अन्तर्गत a_Y = – g त्वरण से स्वतन्त्रतापूर्वक नीचे की ओर t समय में -y दूरी तय की है। चूंकि (ν₀ )y = 0 पर पिण्ड का सम्पूर्ण वेग क्षैतिज दिशा में था; इसलिए इस क्षण ऊध्वधरतः नीचे की ओर प्रारम्भिक वेग (ν₀ )y= 0 तथा (ν₀ )x = ν₀ .

इस समीकरण में (g/2v_0²)= नियतांक अर्थात् समीकरण (3) y = kx² (जहाँ k= g/2ν0²) एक परवलय की प्रदर्शित करती है। अतः सिद्ध होता है कि पृथ्वी से किसी ऊँचाई से क्षैतिज दिशा में प्रक्षेपित पिण्ड का पथ भी परवलयाकार होता है।
उड्डयन काल तथा क्षैतिज परास:
पिण्ड द्वारा O से Q तक पहुँचने में लिया गया समय उड्डयन काल T; होगा तथा इस समय में पिण्ड द्वारा तय की गयी क्षैतिज दूरी OQ= R क्षैतिज परास होगी। इस समय में पिण्ड स्वतन्त्रतापूर्वक [अर्थात् (v₀)_Y = 0] ऊर्ध्वाधरतः नीचे की ओर y = – H दूरी पर गिरता है।

प्रश्न 5:
एक पत्थर मीनार की चोटी से क्षैतिज से 30° का कोण बनाता हुआ 16 मी/से के वेग से ऊपर की ओर फेंका जाता है। उड़ान के 4 सेकण्ड पश्चात् यह पृथ्वी तल पर टकराता है। पृथ्वी से मीनार की ऊँचाई तथा पत्थर का क्षैतिज परास ज्ञात कीजिए। (g = 9.8 मी/से²)।
हल:

प्रश्न 6:
10 मी ऊँची मीनार की चोटी से एक गेंद क्षैतिज से 30° के कोण पर ऊपर की ओर किस | वेग से फेंकी जाए कि गेंद मीनार के आधार से 17.3 मी की दूरी पर जाकर पृथ्वी तल से टकराए? (g= 10 मी/से²)
हल:

We hope the UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane ( समतल में गति) help you.

UP Board Solutions for Class 11 Physics Chapter 4 Motion in a plane (समतल में गति)

Leave a Reply Cancel reply