UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion (गति के नियम)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

(सरलता के लिए आंकिक परिकल्पनाओं में g = 10 ms^-2 लीजिए।)

प्रश्न 1.
निम्नलिखित पर कार्यरत नेट बल का परिमाण व उसकी दिशा लिखिए –
(a) एकसमान चाल से नीचे गिरती वर्षा की कोई बूंद
(b) जल में तैरता 10g संहति का कोई कॉर्क
(c) कुशलता से आकाश में स्थिर रोकी गई कोई पतंग
(d) 30 km h^-1 के एकसमान वेग से ऊबड़-खाबड़ सड़क पर गतिशील कोई कार
(e) सभी गुरुत्वीय पिण्डों से दूर तथा वैद्युत और चुम्बकीय क्षेत्रों से मुक्त, अन्तरिक्ष में तीव्र चाल वाला इलेक्ट्रॉन।
उत्तर :

(a) ∵ त्वरण शून्य है; अत: नेट बल भी शून्य होगा।

(b) ∵ उपरिमुखी गति के समय कॉर्क जल पर स्थिर तैर रहा है अर्थात् गति नहीं हो रही है,
अत : त्वरण शून्य है,
∴नेट बल भी शून्य है।

(c) ∵ पतंग को स्थिर रोका गया है; अत: त्वरण a = 0
∴ नेट बल भी शून्य है।

(d) ∵ कार का वेग एकसमान है; अतः त्वरण a = 0
∴ नेट बल भी शून्य होगा।

(e) ∵ इलेक्ट्रॉन गुरुत्वीय पिण्डों, वैद्युत तथा चुम्बकीय क्षेत्रों से दूर है; अतः उस पर कोई बल नहीं लगेगा।

प्रश्न 2.
0.05 kg संहति का कोई कंकड़ ऊर्ध्वाधर ऊपर फेंका गया है। नीचे दी गई प्रत्येक परिस्थिति में कंकड़ पर लग रहे नेट बल का परिमाण व उसकी दिशा लिखिए –
(a) उपरिमुखी गति के समय।
(b) अधोमुखी गति के समय।
(c) उच्चतम बिन्दु पर जहाँ क्षण भर के लिए यह विराम में रहता है। यदि कंकड़ को क्षैतिज दिशा से 45° कोण पर फेंका जाए, तो क्या आपके उत्तर में कोई परिवर्तन होगा? वायु-प्रतिरोध को उपेक्षणीय मानिए।
उत्तर :
(a) उपरिमुखी गति के समय कंकड़ पर बल = कंकड़ का भार = mg = 0.05 kg × 10 m s^-2 = 0.5 N
(b) अधोमुखी गति के समय भी कंकड़ पर बल उसके भार के बराबर अर्थात् 0.5 N लगेगा।
(c) इस स्थिति में भी कंकड़, पर वही बल 0.5 N ही लगेगा।
कंकड़ को क्षैतिज से 45° के कोण पर फेंकने पर भी कंकड़ पृथ्वी के गुरुत्वीय क्षेत्र में गति करता है; अतः इस स्थिति में भी, प्रत्येक दशा में कंकड़ पर बल 0.5 N ही लगेगा।

प्रश्न 3.
0.1 kg संहति के पत्थर पर कार्यरत नेट बल का परिमाण व उसकी दिशा निम्नलिखित परिस्थितियों में ज्ञात कीजिए –
(a) पत्थर को स्थिर रेलगाड़ी की खिड़की से गिराने के तुरन्त पश्चात्
(b) पत्थर को 36 km h^-1 के एकसमान वेग से गतिशील किसी रेलगाड़ी की खिड़की से गिराने के तुरन्त पश्चात्,
(c) पत्थर को 1 ms^-2 के त्वरण से गतिशील किसी रेलगाड़ी की खिड़की से गिराने के तुरन्त पश्चात्,
(d) पत्थर 1 ms^-2 के त्वरण से गतिशील किसी रेलगाड़ी के फर्श पर पड़ा है तथा वह रेलगाड़ी के सापेक्ष विराम में है।
उपर्युक्त सभी स्थितियों में वायु का प्रतिरोध उपेक्षणीय मानिए।
उत्तर :
(a) स्थिर रेलगाड़ी की खिड़की से गिराने पर, पत्थर पर एकमात्र बल उसका भार नीचे की ओर कार्य करेगा।
∴ पत्थर पर बल = mg = 0.1 kg × 10 m s^-2
= 1N ऊर्ध्वाधर नीचे की ओर।

(b) इस स्थिति में भी गाड़ी से पत्थर गिराने के पश्चात् गाड़ी की गति के कारण उस पर कार्य करने वाले बल का कोई प्रभाव नहीं होगा और पत्थर पर केवल उसका भार कार्य करेगा।
∴ पत्थर पर बल =1N ऊर्ध्वाधर नीचे की ओर।

(c) ∵ पत्थर गाड़ी से नीचे गिरा दिया गया है; अतः अब उस पर केवल उसका भार कार्य करेगा।
∴ पत्थर पर बल 1N ऊर्ध्वाधर नीचे की ओर

(d) ∵ पत्थर रेलगाड़ी के सापेक्ष विराम में है,
∴ पत्थर का त्वरण a = रेलगाड़ी का त्वरण = 1 m s^-2

∴ F = m a से, गाड़ी की त्वरित गति के कारण पत्थर पर नेट बल
F = m a = 0.1 kg × 1 m s^-2
= 0.1 N (क्षैतिज दिशा में)।

पत्थर पर कार्यरत अन्य बल उसका भार तथा फर्श की अभिलम्ब प्रतिक्रिया परस्पर सन्तुलित हो जाते हैं।

प्रश्न 4.
l लम्बाई की एक डोरी का एक सिरा m संहति के किसी कण से तथा दूसरा सिरा चिकनी क्षैतिज मेज पर लगी बँटी से बँधा है। यदि कण चाल से वृत्त में गति करता है तो कण पर (केन्द्र की ओर निर्देशित) नेट बल है-
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 1
उत्तर :

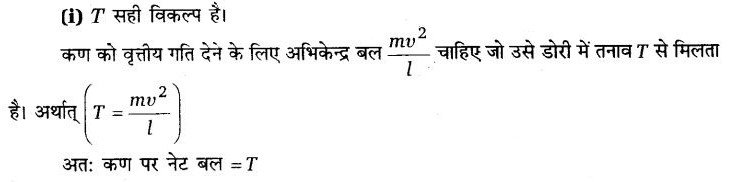
प्रश्न 5.
15 ms^-1 की आरम्भिक चाल से गतिशील 20 kg संहति के किसी पिण्ड पर 50 N का स्थायी मन्दन बल आरोपित किया गया है। पिण्ड को रुकने में कितना समय लगेगा?

प्रश्न 6.
3.0 kg संहति के किसी पिण्ड पर आरोपित कोई बल 25 s में उसकी चाल को 2.0 ms ^-1 से 3.5 ms^-1 कर देता है। पिण्ड की गति की दिशा अपरिवर्तित रहती है। बल का परिमाण व दिशा क्या है?

∴ बल का परिमाण F =mg=3.0 किग्रा x 0.06 मी/से² = 0.18 न्यूटन

चूँकि आरोपित बल का दिशा अपरिवर्तित है तथा यह पिण्ड की चाल को बढ़ा रहा है, अतः बल की दिशा पिण्ड की गति की दम में ही होगी।

प्रश्न 7.
5.0 kg संहति के किसी पिण्ड पर 8 N व 6 N के दो लम्बवत् बल आरोपित हैं। पिण्ड के त्वरण का परिमाण व दिशा ज्ञात कीजिए।

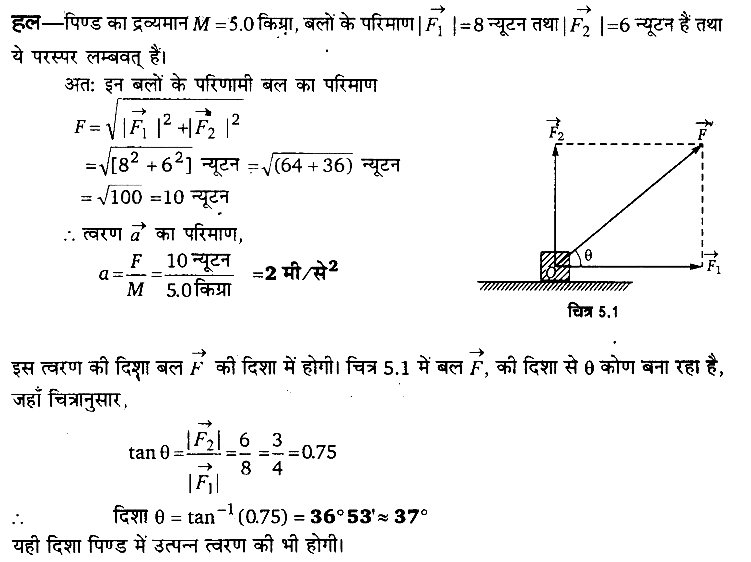
प्रश्न 8.
36 km h^-1 की चाल से गतिमान किसी ऑटो रिक्शा का चालक सड़क के बीच एक बच्चे को खड़ा देखकर अपने वाहन को ठीक 4.0s में रोककर उस बच्चे को बचा लेता है। यदि ऑटो रिक्शा बच्चे के ठीक निकट रुकता है तो वाहन पर लगा औसत मन्द्रन बल क्या है? ऑटो रिक्शा तथा चालक की संहतियाँ क्रमशः 400 kg और 65 kg हैं।
हल :
ऑटो रिक्शा की प्रारम्भिक चाल υ₀ =36 किमी/घण्टा
=36 × (5 / 18) मी/से = 10 मी/से
रुकने पर ऑटो-रिक्शा की अन्तिम चाल υ_t = 0
रुकने में लिया गया समय t = 4.0 सेकण्ड
गति की समीकरण υ_t =υ₀ + at से,
0=10+ a × 4.0
या
मंदक, a=-(10/4) मी/से² = – 2.5 मी/से²
निकाय (ऑटो-रिक्शा + चालक) का द्रव्यमान
M =400 किग्रा +65 किग्रा = 465 किग्रा
∴ औसत मंदन बल F =M × a=465 किग्रा x (-2.5 मी/से2)
=-1.162 × 10³ न्यूटन [यहाँ (-) चिह्न मंदन का प्रतीक है।]

प्रश्न 9.
20000 kg उत्थापन संहति के किसी रॉकेट में 5 ms^-2 के आरम्भिक त्वरण के साथ ऊपर की ओर स्फोट किया जाता है। स्फोट का आरम्भिक प्रणोद (बल) परिकलित कीजिए।

प्रश्न 10.
उत्तर की ओर 10 ms^-1 की एकसमान आरम्भिक चाल से गतिमान 0.40 kg संहति के किसी पिण्ड पर दक्षिण दिशा के अनुदिश 8.0 N का स्थायी बल 30 s के लिए आरोपित किया गया है। जिस क्षण बल आरोपित किया गया उसे । – 0 तथा उस समय पिण्ड की स्थिति x = 0 लीजिए।t – 5s, 25 s, 100 s पर इस कण की स्थिति क्या होगी?

प्रश्न 11.
कोई ट्रक विरामावस्था से गति आरम्भ करके 2.0 ms^-2 के समान त्वरण से गतिशील रहता है। t = 10 s पर, ट्रक के ऊपर खड़ा एक व्यक्ति धरती से 6 m की ऊँचाई से कोई पत्थर बाहर गिराता है।t =11s पर, पत्थर का – (a) वेग तथा (b) त्वरण क्या है? (वायु का प्रतिरोध उपेक्षणीय मानिए।)
हल :
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 11
(a) किसी टुक से पत्थर को गिराते समय पत्थर का क्षैतिज वेग ट्रक के तात्कालिक वेग के बराबर होता है (जड़त्व के कारण) तथ. यह ऊर्ध्वाधर वेग गुरुत्व के कारण प्राप्त करता है जबकि गिराते क्षण ऊर्ध्वाधरत: नीचे की ओर वेग υ0 = शून्य।

प्रश्न 12.
किसी कमरे की छत से 2 m लम्बी डोरी द्वारा 0.1 kg संहति के गोलक को लटकाकर दोलन आरम्भ किए गए। अपनी माध्य स्थिति पर गोलक की चाल 1 ms^-1 है। गोलक का प्रक्षेप्य-पथ क्या होगा यदि डोरी को उस समय काट दिया जाता है जब गोलक अपनी – (a) चरम स्थितियों में से किसी एक पर है तथा (b) माध्य स्थिति पर है?
उत्तर :
(a) चरम स्थिति में गोलक का वेग शून्य होगा; अत: डोरी काट देने पर, गोलक ऊर्ध्वाधर रेखा में नीचे की ओर गिर जाएगा।
(b) माध्य स्थिति में गोलक के पास क्षैतिज दिशा में अधिकतम वेग होगा; अत: इस स्थिति में डोरी काट दिए जाने पर गोलक प्रक्षेप्य की भाँति परवलयाकार पथ पर चलता हुआ अन्त में भूमि पर गिर जाएगा।

प्रश्न 13.
किसी व्यक्ति की संहति 70 kg है। वह एक गतिमान लिफ्ट में तुला पर खड़ा है जो –
(a) 10 ms^-1 की एकसमान चाल से ऊपर जा रही है
(b) 5 ms^-2 के एकसमान त्वरण से नीचे जा रही है
(c) 5 ms^-2 के एकसमान त्वरण से ऊपर जा रही है, तो प्रत्येक प्रकरण में तुला के पैमाने का पाठ्यांक क्या होगा?
(d) यदि लिफ्ट की मशीन में खराबी आ जाए और वह गुरुत्वीय प्रभाव में मुक्त रूप से नीचे गिरे तो पाठ्यांक क्या होगा?
हल :
दिया है। व्यक्ति की संहति m = 70 kg
(a) ∵ लिफ्ट एकसमान वेग से गतिमान है; अत: त्वरण a = 0
∴ तुला का पाठ्यांक R = mg = 70 kg × 9.8 m s ^-2
=686 N

(b) यहाँ लिफ्ट त्वरण a = 5 m s^-2 से नीचे जा रही है
∴ तुला का पाठ्यांक R =m (g – a)
= 70 kg (9.8 – 5) m s^-2
= 336 N

(c) यहाँ लिफ्ट त्वरण a = 5 m s ^-2 से ऊपर जा रही है,
∴ तुला का पाठ्यांक R = m (g + a)
= 70 kg (9.8 + 5) m s ^-2
=1036 N

(d) ∵ लिफ्ट गुरुत्वीय प्रभाव में मुक्त रूप से गिर रही है, अर्थात् a = g
तब, तुला का पाठ्यांक R = m (g – a)
= 70 kg × 0 = 0

प्रश्न 14.
चित्र-5.4 में 4 kg संहति के किसी पिण्ड का स्थिति-समय ग्राफ दर्शाया गया है।
(a) t < 0 ; t > 4 s ; 0 < t,< 4 s के लिए पिण्ड पर आरोपित बल क्या है?
(b) t = 0 तथाt =4 s पर आवेग क्या है? (केवल एकविमीय गति पर विचार कीजिए)
उत्तर :

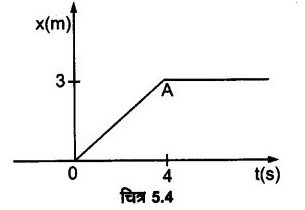
(a) t <0 के लिए स्थिति-समय ग्राफ समय अक्ष के साथ सम्पाती है अर्थात् पिण्ड मूलबिन्दु पर विराम में स्थित है।

∴ पिण्ड पर आरोपित बल शून्य है।
t > 4 s के लिए स्थिति-समय माफ समय अक्ष के समान्तर सरल रेखा है जो बताती है कि इस काल में पिण्ड की मूलबिन्दु से दूरी नियत है।
अर्थात् पिण्ड विराम में है।

∴ पिण्ड पर कार्यरत बल शून्य है।
पुन: 0 < t < 4s के लिए स्थिति समय-ग्राफ एक झुकी हुई सरल रेखा है जो यह बताती है कि इस काल में पिण्ड की मूलबिन्दु से दूरी नियत दर से बढ़ रही है।

अर्थात् पिण्ड नियत वेग से गति कर रहा है; अतः उसको त्वरण शून्य है।

∴ पिण्ड पर आरोपित बल शून्य है।

प्रश्न 15.
किसी घर्षणरहित मेज पर रखे 10 kg तथा 20kg के दो पिण्ड किसी पतली डोरी द्वारा आपस में जुड़े हैं। 600 N का कोई क्षैतिज बल (i) A पर, (ii) B पर डोरी के अनुदिश लगाया जाता है। प्रत्येक स्थिति में डोरी में तनाव क्या है?

प्रश्न 16.
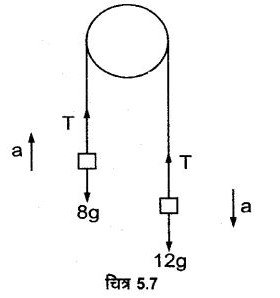
8 kg तथा 12kg के दो पिण्डों को किसी हल्की अवितान्य डोरी, जो घर्षणरहित घिरनी पर चढ़ी है, के दो सिरों से बाँधा गया है। पिण्डों को मुक्त रूप से छोड़ने पर उनके त्वरण तथा डोरी में तनाव ज्ञात कीजिए।
हल – माना पिण्डों को मुक्त छोड़ने पर भारी पिण्ड a त्वरण से नीचे की ओर उतरता है। चूंकि डोरी अवितान्य है; अत: हल्का पिण्ड त्वरण से ऊपर की ओर चढ़ेगा।
माना डोरी में तनाव T है, जो कि पूरी डोरी में एकसमान होगा।
भारी अर्थात् 12 kg के पिण्ड पर नेट बल F = 12g – T नीचे की ओर कार्य करेगा।

प्रश्न 17.
अयोगशाला के निर्देश फ्रेम में कोई नाभिक विराम में है। यदि यह नाभिक दो छोटे नाभिकों में विघटित हो जाता हैं तो यह दर्शाइए कि उत्पाद विपरीत दिशाओं में गति करने चाहिए।
उत्तर :
माना नाभिक का द्रव्यमान m है तथा प्रश्नानुसार यह विराम में है अर्थात् $\xrightarrow { v }$ = 0
∴ नाभिक को प्रारम्भिक संवेग = m × 0 = 0
माना इसके टूटने से बने दो नाभिकों के द्रव्यमान m₁ तथा m₂ हैं तथा ये क्रमशः $\xrightarrow { v1 }$ तथा $\xrightarrow { v2 }$ वेगों से गति करते हैं।
अतः इन नए नाभिकों का कुल संवेग = m1 $\xrightarrow { v 1}$ + m2 $\xrightarrow { v2 }$
∵ नाभिक स्वतः विघटित हुआ है अर्थात् उस पर बाह्य बल शून्य है; अत: निकाय का संवेग संरक्षित रहेगा।
∴ विघटन के बाद कुल संवेग = विघटन के पूर्व कुल संवेग

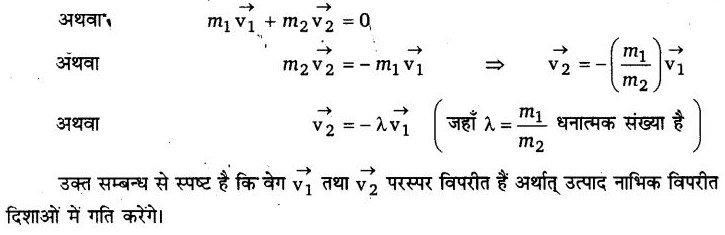
प्रश्न 18.
दो बिलियर्ड गेंद जिनमें प्रत्येक की संहति 0.05 kg है, 6 मी / से^-1 की चाल से विपरीत . दिशाओं में गति करती हुई संघट्ट करती हैं और संघट्ट के पश्चात् उसी चाल से वापस लौटती हैं। प्रत्येक गेंद पर दूसरी गेंद कितना आवेग लगाती है?
हल :
संघट्ट के पश्चात् प्रत्येक गेंद के वेग की दिशा उलट जाती है। अत: प्रत्येक गेंद के वेग में परिवर्तन का परिमाण
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 22

प्रश्न 19.
100 kg संहति की किसी तोप द्वारा 0.020 kg का गोला दागा जाता है। यदि गोले की नालमुखी चाल 80 मी/से^-1 है तो तोप की प्रतिक्षेप चाल क्या है?
हल :
तोप का द्रव्यमान M =100 किग्रा
गोले का द्रव्यमान m=0.020 किग्रा
गोले की नालमुखी चाल =80 मी/से
माना तोप की प्रतिक्षेप चाल =V मी/से
प्रारम्भ में गोला व तोप दोनों विरामावस्था में हैं। अत: प्रारम्भ में प्रत्येक का संवेग शून्य था।
अतः रेखीय संवेग-संरक्षण नियम के अनुसार,
तोप तथा गोले का अन्तिम संवेग = प्रारम्भिक संवेग
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 23
यहाँ (-) चिह्न इस तथ्य का प्रतीक है कि तोप का वेग गोले के वेग की विपरीत दिशा में होगा। इसीलिए इसको प्रतिक्षेप चाल कहते हैं। अत: तोप की प्रतिक्षेप चाल = 0.016 सेमी/से।

प्रश्न 20.
कोई बल्लेबाज किसी गेंद को 45° के कोण पर विक्षेपित कर देता है। ऐसा करने में वह गेंद की आरम्भिक चाल, जो 54 km/h^-1 है, में कोई परिवर्तन नहीं करता। गेंद को कितना आवेग दिया जाता है? (गेंद की संहति 0.15 kg है)
हल :
माना गेंद पथ AB के अनुदिश बल्लेबाज की ओर υ = 54 किमी/घण्टा =54 × (5 / 18) मी/से = 15 मी/से की चाल से आ रही है। यह बिन्दु B पर बल्लेबाज द्वारा उसी चाल से कोण ABC =45° पर पथ BC के अनुदिश विक्षेपित कर दी जाती है। B से गुजरते ऊर्ध्वाधर तल पर X’ BX अभिलम्ब है।

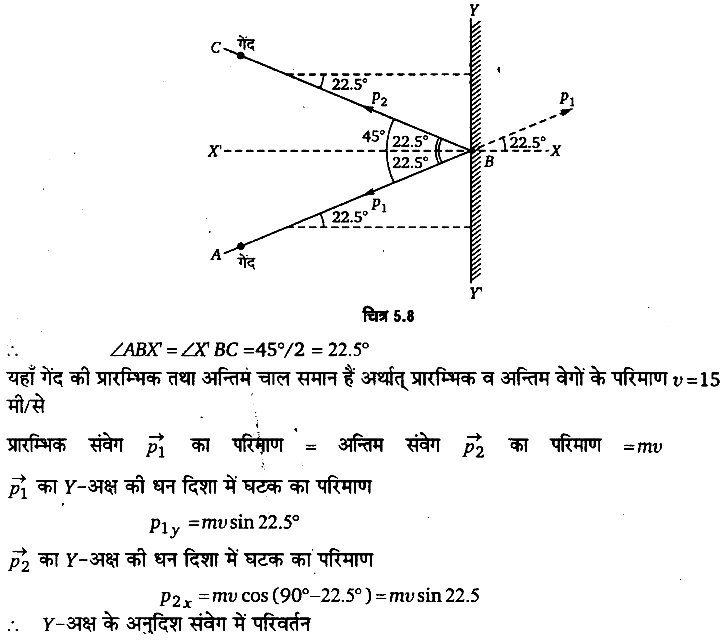
प्रश्न 21.
किसी डोरी के एक सिरे से बँधा 0.25 kg संहति का कोई पत्थर क्षैतिज तल में 1.5 m त्रिज्या के वृत्त पर 40 rev/min की चाल से चक्कर लगाता है। डोरी में तनाव कितना है? यदि डोरी 200 N के अधिकतम तनाव को सहन कर सकती है, तो वह अधिकतम चाल ज्ञात कीजिए जिससे पत्थर को घुमाया जा सकता है।
हल :
दिया है : पत्थर का द्रव्यमान m=0.25 kg

प्रश्न 22.
यदि अभ्यास प्रश्न 21 में पत्थर की चाल को अधिकतम निर्धारित सीमा से भी अधिक कर दिया जाए तथा डोरी यकायक टूट जाए, तो डोरी के टूटने के पश्चात पत्थर के प्रक्षेप का सही वर्णन निम्नलिखित में से कौन करता है –
(a) वह पत्थर झटके के साथ त्रिज्यतः बाहर की ओर जाता है।
(b) डोरी टूटने के क्षण पत्थर स्पर्शरेखीय पथ पर उड़ जाता है।
(c) पत्थर स्पर्शी से किसी कोण पर, जिसका परिमाण पत्थर की चाल पर निर्भर करता है, उड़ जाता है।
उत्तर :
(b) डोरी टूटने के क्षण पत्थर स्पर्शरेखीय पथ पर उड़ जाता है क्योंकि उस क्षण पर पत्थर की चाल स्पर्शरेखीय होती है।

प्रश्न 23.
स्पष्ट कीजिए कि क्यों :
(a) कोई घोड़ा रिक्त दिकस्थान (निर्वात) में किसी गाड़ी को खींचते हुए दौड़ नहीं सकता।
(b) किसी तीव्र गति से चल रही बस के यकायक रुकने पर यात्री आगे की ओर गिरते हैं।
(c) लान मूवर को धकेलने की तुलना में खींचना आसान होता है।
(d) क्रिकेट का खिलाड़ी गेंद को लपकते समय अपने हाथ गेंद के साथ पीछे को खींचता है।
उत्तर :

(a) रिक्त दिक्स्थान (निर्वात) में घोड़े को गाड़ी खींचने के लिए आवश्यक प्रतिक्रिया नहीं मिल पाएगी।

(b) तीव्र गति से गतिशील बस में बैठे यात्री का शरीर गाड़ी के ही वेग से गति करता रहता है। जब यकायक गाड़ी रुकती है तो फर्श के सम्पर्क में स्थित यात्री के पैर तो ठीक उसी समय विराम में आ जाते हैं, परन्तु गति के जड़त्व के कारण ऊपर का शरीर गतिशील बना रहता है और यात्री आगे की ओर गिर जाते हैं।

(c) लान मूवर को धकेलने की अपेक्षा खींचना आसान है – मान लीजिए कि चित्र-5.9 (a) के अनुसार एक लान मूवर को धकेलकर ले जाया जा रहा है। इसके लिए हम मूवर के हत्थे के अनुदिश एक बल $\xrightarrow { F }$ लगाते हैं, जो क्षैतिज से नीचे की ओर θ कोण (माना) पर कार्य करता है। मूवर पर कार्यरत अन्य बल, उसका भार Mg, भूमि की अभिलम्ब प्रतिक्रिया N तथा पश्चमुखी घर्षण बल ƒ₁ है।
∵ ऊध्र्वाधर दिशा में कोई गति नहीं है।
अतः इस दिशा में नेट बल शून्य होगा।

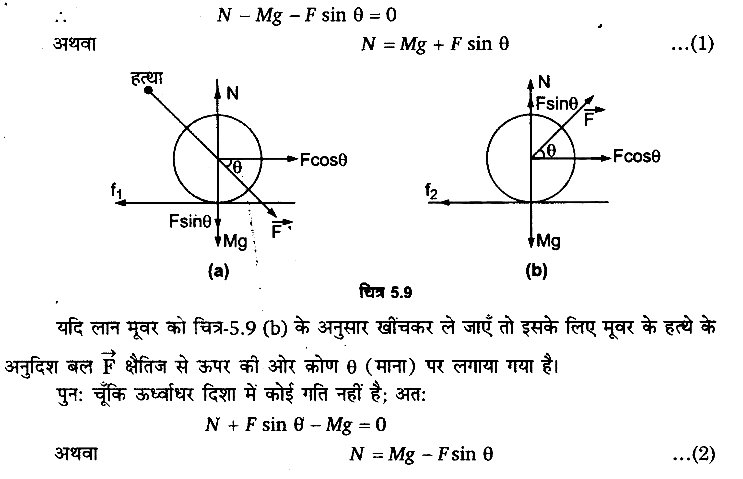
समीकरण (1) व (2) से स्पष्ट है कि मूवर को खींचते समये अभिलम्ब प्रतिक्रिया उसे धकेलते समय अभिलम्ब प्रतिक्रिया से कम है। चूंकि सीमान्त घर्षण बल अभिलम्ब प्रतिक्रिया के अनुक्रमानुपाती होता है; अतः मूवर को खींचते समय अपेक्षाकृत कम घर्षण बल लगेगा। इससे स्पष्ट है कि मूवर को खींचकर ले जाना धकेलकर ले जाने की तुलना में आसान होता है।

(d) क्रिकेट का खिलाड़ी गेंद को लपकते समय अपने हाथ गेंद के साथ पीछे को खींचता है – ऐसा करने में गेंद को विराम में आने तक पर्याप्त समय मिल जाता है, इससे गेंद के संवेग की परिवर्तन की दर कम हो जाती है और हाथों पर लगने वाला बल घट जाता है फलस्वरूप चोट लगने की सम्भावना कम हो जाती है।

अतिरिक्त अभ्यास

प्रश्न 24.
चित्र 5.10 में 0.04kg संहति के किसी पिण्ड का स्थिति-समय ग्राफ दर्शाया गया है। इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिए। पिण्ड द्वारा प्राप्त दो क्रमिक आवेगों के बीच समय-अन्तराल क्या है? प्रत्येक आवेग का परिमाण क्या है?
हल :
यह स्थिति-समय ग्राफ दो समान्तर ऊर्ध्वाधर दीवारों के बीच एकसमान चाल से क्षैतिज गति करती हुई गेंद का ग्राफ हो सकता है, जो बारम्बार एक दीवार से टकराती है फिर 2s बाद दूसरी दीवार से टकराती है। यह क्रिया लगातार चलती है।
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 28

पिण्ड के वेग में प्रत्येक 2 s के अन्तराल के बाद परिवर्तन आता है।

प्रश्न 25.
चित्र 5.11 में कोई व्यक्ति 1 ms^-2 त्वरण से गतिशील क्षैतिज संवाहक पट्टे पर स्थिर खड़ा है। उस व्यक्ति पर आरोपित नेट बल क्या है? यदि व्यक्ति के जूतों और पट्टे के बीच स्थैतिक घर्षण गुणांक 0.2 है तो पट्टे के कितने त्वरण तक वह व्यक्ति उस पट्टे के सापेक्ष स्थिर रह सकता है? (व्यक्ति की संहति = 65 kg)
हल :

(i) दिया है : पट्टे का त्वरण a = 1 m s ^-2, व्यक्ति का द्रव्यमान m = 65 kg
∵ व्यक्ति पट्टे पर स्थिर खड़ा है; अत: व्यक्ति का त्वरण भी a = 1 m s ^-2 है।
सूत्र F = m a से,
व्यक्ति पर आरोपित नेट बल F = 65 kg × 1 m s ^-2 = 65 N

(ii) व्यक्ति के जूतों और पट्टे के बीच स्थैतिक घर्षण गुणांक µs = 0.2
∵ पट्टा क्षैतिज है; अतः मनुष्य पर पट्टे की अभिलम्ब प्रतिक्रिया
N = mg = 65 kg × 10 m s ^-2 = 650 N
माना पट्टे का अधिकतम त्वरण a है, तब पट्टे के साथ गति करने के लिए व्यक्ति को ma के बराबर बल की आवश्यकता होगी जो उसे स्थैतिक घर्षण से मिलेगा।
इसके लिए आवश्यक है कि
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 30

प्रश्न 26.
m संहति के पत्थर को किसी डोरी के एक सिरे से बाँधकर R त्रिज्या के ऊर्ध्वाधर वृत्त में घुमायो जाता है। वृत्त के निम्नतम तथा उच्चतम बिन्दुओं पर ऊर्ध्वाधरतः अधोमुखी दिशा में नेट बल है- (सही विकल्प चुनिए)
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 31
उत्तर :
निम्नतम बिन्दु पर तनाव T₁ ऊपर की ओर, भार mg नीचे की ओर है।
∴ नेट अधोमुखी बल = mg – T₁
उच्चतम बिन्दु पर तनाव T₂ व भार mg दोनों नीचे की ओर लगेंगे।
∴ नेट अधोमुखी बल = mg + T₂
अतः विकल्प (i) सही है।

प्रश्न 27.
1000 kg संहति का कोई हेलीकॉप्टर 15 ms-2 के ऊध्र्वाधर त्वरण से ऊपर उठता है। चालक दल तथा यात्रियों की संहति 300 kg है। निम्नलिखित बलों का परिमाण व दिशा लिखिए –
(a) चालक दल तथा यात्रियों द्वारा फर्श पर आरोपित बल
(b) चारों ओर की वायु पर हेलीकॉप्टर के रोटर की क्रिया, तथा
(c) चारों ओर की वायु के कारण हेलीकॉप्टर पर आरोपित बल।

प्रश्न 28.
15 ms^-1 चाल से क्षैतिजतः प्रवाहित कोई जलधारा 10 ^-2 मी ² अनुप्रस्थ काट की किसी नली से बाहर निकलती है तथा समीप की किसी ऊर्ध्वाधर दीवार से टकराती है। जल की टक्कर द्वारा, यह मानते हुए कि जलधारा टकराने पर वापस नहीं लौटती, दीवार पर आरोपित बल ज्ञात कीजिए।
हल :
नली के अनुप्रस्थ काट का क्षेत्रफल A=10 ^-2 मी ²
इससे निकलने वाली जल-धारा का वेग अर्थात् प्रति सेकण्ड तय की दूरी
υ=15 मी/से
∴ नली से निकलकर दीवार पर प्रति सेकण्ड लम्बवत् टकराने वाले जल को आयतन =A × υ
अतः दीवार पर प्रति सेकण्ड लम्बवत् टकराने वाले जल का द्रव्यमान
m= आयतन × जल का घनत्व =A × υ × p
जल का घनत्व, p =10³ किग्रा/मी ³
m =10^-2 मी² × 15 मी/से x 10³ किग्रा/मी³ =150 किग्रा
चूँकि दीवार पर टकराने पर जल-धारा वापस नहीं लौटती है अर्थात् उसका वेग शून्य हो जाता है, अत: ∆t =1 सेकण्ड में जल-धारा के संवेग में परिवर्तन,

प्रश्न 29.
किसी मेज पर एक-एक रुपये के दस सिक्कों को एक के ऊपर एक करके रखा गया है। प्रत्येके सिक्के की संहतिm है। निम्नलिखित प्रत्येक स्थिति में बल का परिमाण एवं दिशा लिखिए
(a) सातवें सिक्के (नीचे से गिनने पर) पर उसके ऊपर रखे सभी सिक्कों के कारण बल
(b) सातवें सिक्के पर आठवें सिक्के द्वारा आरोपित बल, तथा
(c) छठे सिक्के की सातवें सिक्के पर प्रतिक्रिया।
हल :

(a) नीचे से सातवें सिक्के के ऊपर तीन सिक्के रखे हैं।
अतः सातवाँ सिक्का इन तीन सिक्कों के भार के बराबर बल का अनुभव करेगा।
∴ सातवें सिक्के पर ऊपर के सिक्कों के कारण बल = 3 mg N

(b) आठवें सिक्के के ऊपर दो सिक्के और रखे हैं; अत: सातवें सिक्के पर आठवें सिक्के के कारण बल, आठवें सिक्के तथा ऊपर के दो सिक्कों के भारों के योग के बराबर होगा।
∴सातवें सिक्के पर आठवें सिक्के के कारण बल = mg + 2 mg= 3 mg N

(c) सातवें सिक्के के ऊपर तीन सिक्के रखे हैं; अत: सातवाँ सिक्का अपने तथा ऊपर के तीन सिक्कों के भारों के योग के बराबर बल से छठवें सिक्के को दबाएगा।
अत: छठे सिक्के पर सातवें के कारण बल = mg + 3 mg = 4 mgN
∴ छठवें सिक्के की सातवें पर प्रतिक्रिया = 4mg N

प्रश्न 30.
कोई वायुयान अपने पंखों को क्षैतिज से 15° के झुकाव पर रखते हुए 720 kmh^-1 की चाल से एक क्षैतिज लूप पूरा करता है। लूप की त्रिज्या क्या है?
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 35

प्रश्न 31.
कोई रेलगाड़ी बिना ढाल वाले 30 m त्रिज्या के वृत्तीय मोड़ पर 54 kmh^-1 की चाल से चलती है। रेलगाड़ी की संहति 10⁶ kg है। इस कार्य को करने के लिए आवश्यक अभिकेन्द्र बल कौन प्रदान करता है, इंजन अथवा पटरियाँ ? पटरियों को क्षतिग्रस्त होने से बचाने के लिए मोड़ का ढाल-कोण कितना होना चाहिए?
हल :
आवश्यक अभिकेन्द्र बल पटरियाँ प्रदान करती हैं।

प्रश्न 32.
चित्र-5.14 में दर्शाए अनुसार 50 kg संहति का कोई व्यक्ति 25 kg संहति के किसी गुटके को दो भिन्न ढंग से उठाता है। दोनों स्थितियों में उस व्यक्ति द्वारा फर्श पर आरोपित क्रिया-बल कितना है? यदि 700 N अभिलम्ब बल से फर्श धंसने लगता है तो फर्श को धंसने से बचाने के लिए उस व्यक्ति को गुटके को उठाने के लिए कौन-सा ढंग अपनाना चाहिए?
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 37

इसलिए फर्श द्वारा व्यक्ति पर आरोपित ऊर्ध्वाधर बल
F’ = W₂ + F = (500 + 250) न्यूटन = 750 न्यूटन

(b) चित्र 5.15 (b) में व्यक्ति द्वारा बल F नीचे की ओर लगाया जा रहा है। अतः फर्श पर प्रतिक्रिया R = F ऊपर की ओर होगी।
अतः फर्श द्वारा व्यक्ति पर आरोपित लम्बवत् बल F” = W2 – F
F” = 500 न्यूटन – 250 न्यूटन = 250 न्यूटन
∵ दिया है कि फर्श 700 न्यूटन के लम्बवत् बल से नीचे धंसने लगता है, अत: उपर्युक्त विवेचना से स्पष्ट है कि व्यक्ति को गुटके को उठाने के लिए विधि (b) अपनानी चाहिए।

प्रश्न 33.
40 kg संहति का कोई बन्दर 600 N का अधिकतम तनाव सह सकने योग्य किसी रस्सी पर चढता है (चित्र-5.16)। नीचे दी गई स्थितियों में से किसमें रस्सी टूट जाएगी –
(a) बन्दर 6 ms ^-2 त्वरण से ऊपर चढ़ता है
(b) बन्दर 4ms ^-2 त्वरण से नीचे उतरता है
(c) बन्दर 5 ms ^-2 की एकसमान चाल से ऊपर चढ़ता है,
(d) बन्दर लगभग मुक्त रूप से गुरुत्व बल के प्रभाव में रस्सी से गिरता है। (रस्सी की संहति उपेक्षणीय मानिए)
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 40 हल :

(a) माना बन्दर का द्रव्यमान m है, तब गुरुत्व के कारण उसका भार mg है। माना रस्सी में उत्पन्न तनाव T है।
जब बन्दर रस्सी के सहारे ऊपर की ओर त्वरित गति करे, तब
T₁-mg= ma₁
अर्थात् डोरी में तनाव,
T₁ =ma₁ +mg = m(a₁ +g)
= 40 किग्रा x (6+10) मी/से ² =640 न्यूटन
T₁ > 600 न्यूटन (अतः रस्सी टूट जायेगी)

(b) जब बन्दर नीचे को त्वरित गति करे, तब
mg -T₂ = ma₂
या डोरी में तनाव, T₂ =m(g-a₂)
= 40 × (10 – 4) न्यूटन = 240 न्यूटन
T₂ <600 न्यूटन (अतः रस्सी नहीं टूटेगी।)

(c) जब बन्दर रस्सी के सहारे ऊपर चढ़नी शुरू करे, तब
a₃ = 0
∴ T₃ – mg = ma₃ = 0
या
T3 = mg
∴ डोरी में तनाव, T₃ =40 × 10 न्यूटन = 400 न्यूटन
इस दशा में भी T₃ <600 न्यूटन (अतः रस्सी नहीं टूटेगी।)

(d) जब बन्दर मुक्त रूप से नीचे उतरता है तो बन्दर भारहीनता की अवस्था में होगा अर्थात् डोरी में तनाव शून्य होगा।
चूँकि नीचे उतरने की दशा में,
T = m (g-d) तथा यहाँ a = g
T = 0 (अतः रस्सी नहीं टूटेगी।)

केवल स्थिति (a) में रस्सी टूटेगी क्योंकि इसमें महत्तम तनाव 600 न्यूटन से अधिक है।

प्रश्न 34.
दो पिण्ड A तथा B, जिनकी संहति क्रमशः 5 kg तथा 10 kg है-एक-दूसरे के सम्पर्क में एक मेज पर किसी दृढ विभाजक दीवार के सामने विराम में रखे हैं। (चित्र-5.17)। पिण्डों तथा मेज के बीच घर्षण गुणांक A B E 0.15 है। 200 N का कोई बल क्षैतिजतः A पर आरोपित किया जाता है।
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 41 (a) विभाजक दीवार की प्रतिक्रिया तथा
(b) A तथा B के बीच क्रिया-प्रतिक्रिया बल क्या है? विभाजक दीवार को हटाने पर क्या होता है? यदि पिण्ड गतिशील है तो क्या (b) का उत्तर बदल जाएगा? µ_s तथा µ_k के बीच अन्तर की उपेक्षा कीजिए।

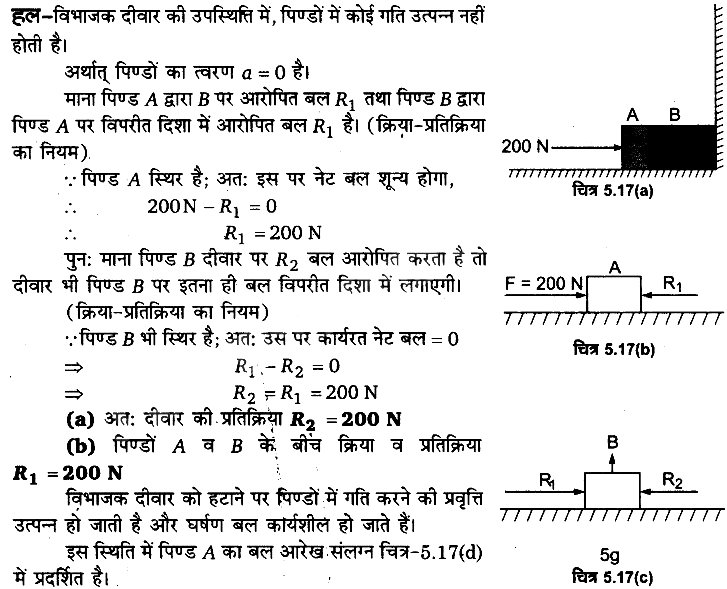
प्रश्न 35.
15 kg संहति का कोई गुटका किसी लंबी ट्रॉली पर रखा है। गुटके तथा ट्रॉली के बीच स्थैतिक घर्षण गुणांक 0.18 है। ट्रॉली विरामावस्था से 20 s तक 0.5 ms^-2 के त्वरण से त्वरित होकर एकसमान वेग से गति करने लगती है- (a) धरती पर स्थिर खड़े किसी प्रेक्षक को तथा (b) ट्रॉली के साथ गतिमान किसी अन्य प्रेक्षक को, गुटके की गति कैसी प्रतीत होगी, इसकी विवेचना कीजिए।
हल :
गुटके का द्रव्यमान m = 15 kg, µ = 0.18
t = 20s के लिए, ट्रॉली का त्वरण a1 = 0.5 m s^-2
तत्पश्चात् ट्रॉली का वेग अचर है।
∵प्रारम्भ में ट्रॉली त्वरित गति करती है; अत: यह एक अजड़त्वीय निर्देश तन्त्र है।
∴ गुटके पर एक छद्म बल F₁ =ma₁ =15 × 0.5 = 7.5 N
पीछे की ओर कार्य करेगा।
जबकि ट्रॉली के फर्श द्वारा गुटके पर आरोपित अग्रगामी घर्षण बल
F₂ =µ N.=µm g = 0.18 × 15 × 10 = 27 N
∵ गुटके पर पश्चगामी बेल घर्षण बल की तुलना में कम है; अतः गुटका पीछे की ओर नहीं फिसलेगा और ट्रॉली के साथ-साथ गति करेगा।
(a) धरती पर खड़े स्थिर प्रेक्षक को गुटका ट्रॉली के साथ गति करता प्रतीत होगा।
(b) ट्रॉली के साथ गतिमाने प्रेक्षक को गुटका स्वयं के सापेक्ष विराम अवस्था में दिखाई देगा।

प्रश्न 36.
चित्र-5.18 में दर्शाए अनुसार किसी ट्रक का पिछला भाग खुला है तथा 40 kg संहति का एक सन्दूक खुले सिरे से 5 m दूरी पर रखा है। ट्रक के फर्श तथा संदूक के बीच घर्षण गुणांक 0.15 है। किसी सीधी सड़क पर ट्रक विरामावस्था से गति प्रारम्भ करके 2m s^-2 से त्वरित होता है। आरम्भ बिन्दु से कितनी दूरी चलने पर वह सन्दूक ट्रक से नीचे गिर जाएगा? (सन्दूक के आमाप की उपेक्षा कीजिए।)

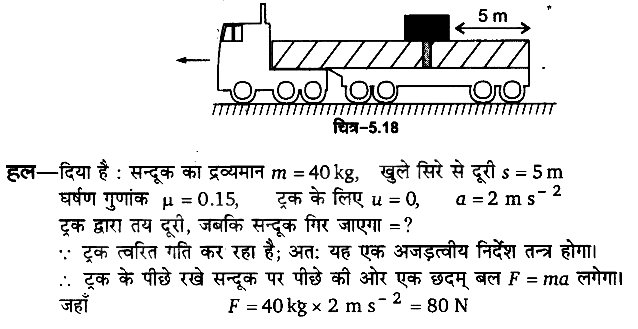
प्रश्न 37.
15 cm त्रिज्या का कोई बड़ा ग्रामोफोन रिकार्ड 33 $\cfrac { 1 }{ 3 }$ rev/min की चाल से घूर्णन कर रहा है। रिकार्ड पर उसके केन्द्र से 4cm तथा 14 cm की दूरियों पर दो सिक्के रखे गए हैं। यदि सिक्के तथा रिकार्ड के बीच घर्षण गुणांक 0.15 है तो कौन-सा सिक्का रिकार्ड के साथ परिक्रमा करेगा?

प्रश्न 38.
आपने सरकस में ‘मौत के कुएँ (एक खोखला जालयुक्त गोलीय चैम्बर ताकि उसके भीतर के क्रियाकलापों को दर्शक देख सकें) में मोटरसाइकिल सवार को ऊध्र्ध्वाधर लूप में मोटरसाइकिल चलाते हुए देखा होगा। स्पष्ट कीजिए कि वह मोटरसाइकिल सवार नीचे से कोई सहारा न होने पर भी गोले के उच्चतम बिन्दु से नीचे क्यों नहीं गिरता? यदि चैम्बर की त्रिज्या 25 m है तो ऊर्ध्वाधर लूप को पूरा करने के लिए मोटरसाइकिल की न्यूनतम चाल कितनी होनी चाहिए?
हल :
गोलीय चैम्बर के उच्चतम बिन्दु पर मोटरसाइकिल सवार चैम्बर को बाहर की ओर दबाता है और प्रतिक्रिया स्वरूप चैम्बर सवार पर गोले के केन्द्र की ओर दिष्ट प्रतिक्रिया R लगाता है। सवार वे मोटरसाइकिल का भार mg भी गोले के केन्द्र की ओर कार्य करते हैं। ये दोनों बल सवार को वृत्तीय गति करने के लिए आवश्यक अभिकेन्द्र बल प्रदान करते हैं, जिसके कारण सवार नीचे नहीं गिर पाता।
इस बिन्दु पर गति की समीकरण
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 48 R + mg = mυ² / r
जहाँ υ सवार की चाल तथा r गोले की त्रिज्या है।

ऊर्ध्वाधर लूप को पूरा पार करने के लिए उच्चतम बिन्दु पर न्यूनतम चाल (क्रान्तिक चाल)
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 49

प्रश्न 39.
70 kg संहति का कोई व्यक्ति अपने ऊध्र्वाधर अक्ष पर 200 rev/min की चाल से घूर्णन करती 3m त्रिज्या की किसी बेलनाकार दीवार के साथ उसके सम्पर्क में खड़ा है। दीवार तथा उसके कपड़ों के बीच घर्षण गुणांक 0.15 है। दीवार की वह न्यूनतम घूर्णन चाल ज्ञात कीजिए, जिससे फर्श को यकायक हटा लेने पर भी, वह व्यक्ति बिनागिरे दीवार से चिपका रह सके।

प्रश्न 40.
R त्रिज्याका पतला वृत्तीय तार अपने ऊर्ध्वाधरं व्यास के परितः कोणीय आवृत्ति से घूर्णन कर रहा है। यह दर्शाइए कि इस तार में डली कोई मणिका ω ≤ $\sqrt { \frac { g }{ R } }$ के लिए अपने निम्नतम बिन्दु पर रहती है। ω = $\sqrt { \frac { 2g }{ R } }$ के लिए, केन्द्र से मनके को जोड़ने वाला त्रिज्य सदिश ऊर्ध्वाधर अधोमुखी दिशा से कितना कोण बनाता है? (घर्षण को उपेक्षणीय मानिए)
हल :
माना कि मणिका का द्रव्यमान m है तथा किसी क्षण मणिका को वृत्तीय तार के केन्द्र से मिलाने वाली त्रिज्या ऊर्ध्वाधर से θ कोण पर झुकी है।
इस समय मणिका पर दो बल लगे हैं –
(1) वृत्तीय तार की अभिलम्ब प्रतिक्रिया N केन्द्र O की ओर।
(2) भूमिका का भार mg नीचे की ओर।
मणिका वृत्तीय तार के साथ PQ = r त्रिज्या के वृत्तीय पथ पर घूम रही है, जिसका केन्द्र Q है।
जहाँ r = PQ=OP sin 8 = R sin θ
प्रतिक्रिया N की ऊर्ध्वाधर तथा क्षैतिज घटकों में वियोजित करने पर, ऊध्र्वाधर घटक N cos θ भार को सन्तुलित करता है।
अर्थात् N cos θ = mg
क्षैतिज घटक N sin θ, अभिकेन्द्र बल mr ω² प्रदान करता है।
अर्थात् N sin θ mr ω²
N sin θ =m (R sin θ) ω²
N = mR ω²
समी० (1) में मान रखने पर,
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 51

परीक्षापयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न

प्रश्न 1.
किसी वस्तु पर एक नियत बल लगाने से वस्तु गति करती है।
(i) एकसमान वेग से
(ii) एकसमान त्वरण से
(iii) असमान त्वरण से
(iv) असमान वेग से
उत्तर :
(ii) एकसमान त्वरण से

प्रश्न 2.
जब किसी वस्तु की गति में त्वरण उत्पन्न होता है, तब
(i) वह सदैव पृथ्वी की ओर गिरती है।
(ii) उसकी चाल में सदैव वृद्धि होती है।
(iii) उस पर सदैव कोई बल कार्य करता है।
(iv) उसकी गति की दिशा बदल जाती है।
उत्तर :
(iii) उस पर सदैव कोई बल कार्य करता है।

प्रश्न 3.
एक क्षैतिज सड़क पर कार की त्वरित गति उस बल के कारण होती है जो
(i) कार के इंजन द्वारा लगाया जाता है।
(ii) कार के ड्राइवर द्वारा लगाया जाता है
(iii) पृथ्वी द्वारा लगाया जाता है।
(iv) सड़क द्वारा लगाया जाता है।
उत्तर :
(iv) सड़क द्वारा लगाया जाता है

प्रश्न 4.
एक फुटबॉल तथा उसी आकार के एक पत्थर के जड़त्व में से
(i) फुटबॉल का जड़त्व अधिक है।
(ii) पत्थर का जड़त्व अधिक है।
(iii) दोनों का जड़त्व बराबर है।
(iv) इनमें से कोई नहीं
उत्तर :
(ii) पत्थर का जड़त्व अधिक है।

प्रश्न 5.
किसी लिफ्ट में वस्तु को भार कम प्रतीत होगा, जबकि लिफ्ट
(i) एकसमान वेग से नीचे उतरती है
(ii) एकसमान वेग से ऊपर जाती है।
(iii) त्वरण के साथ ऊपर जाती है।
(iv) मन्दन के साथ ऊपर जाती है।
उत्तर :
(iv) मन्दन के साथ ऊपर जाती है।

प्रश्न 6.
एक हल्की डोरी घर्षण रहित घिरनी के ऊपर से गुजरती है। उसके एक सिरे पर m तथा दूसरे सिरे पर 3m के द्रव्यमान बँधे हैं, निकाय का त्वरण होगा।
(i) g/4
(ii) g/3
(iii) g/2
(iv) g
उत्तर :
(iii) g/2

प्रश्न 7.
एक घोड़ा गाड़ी को खींचता है तो जो बल घोड़े को आगे बढ़ने में सहायता करता है, वह लगाया जाता है
(i) गाड़ी द्वारा घोड़े पर
(ii) पृथ्वी द्वारा घोड़े पर
(iii) पृथ्वी द्वारा गाड़ी पर
(iv) घोड़े द्वारा पृथ्वी पर
उत्तर :
(ii) पृथ्वी द्वारा घोड़े पर

प्रश्न 8.
200 किग्रा द्रव्यमान की लिफ्ट 3.0 मी/से2 के त्वरण से ऊपर की ओर गति कर रही है। यदि g = 10 मी/से2 हो तो लिफ्ट की डोरी का तनाव होगा
(i) 2600 न्यूटन
(ii) 2000 न्यूटन
(iii) 1300 न्यूटन
(iv) 600 न्यूटन
उत्तर :
(i) 2600 न्यूटन

प्रश्न 9.
रॉकेट-नोदन की कार्य विधि आधारित है।
(i) ‘न्यूटन के प्रथम नियम पर
(ii) संवेग संरक्षण के सिद्धान्त पर
(iii) द्रव्यमान संरक्षण के सिद्धान्त पर
(iv) न्यूटन के द्वितीय नियम पर
उत्तर :
(iii) द्रव्यमान संरक्षण के सिद्धान्त पर

प्रश्न 10.
न्यूटन के गति के द्वितीय नियम के अनुसार, किसी पिण्ड पर आरोपित बल समानुपाती होता है।
(i) उसके संवेग परिवर्तन के
(ii) उसके द्रव्यमान तथा वेग के गुणनफल के
(iii) उसके द्रव्यमान तथा त्वरण के गुणनफल के
(iv) उपर्युक्त में से कोई नहीं
उत्तर :
(i) उसके द्रव्यमान तथा वेग के गुणनफल के

प्रश्न 11.
गेंद कैच करते समय क्रिकेट खिलाड़ी अपने हाथ नीचे कर लेता है, क्योंकि
(i) उसके हाथ घायल होने से बच जाएँगे
(ii) वह गेंद को मजबूती से पकड़ लेता है।
(iii) वह खिलाड़ी को धोखा देता है।
(iv) उपर्युक्त में से कोई नहीं
उत्तर :
(iv) उपर्युक्त में से कोई नहीं

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
1 न्यूटन बल की परिभाषा दीजिए।
उत्तर :
1 न्यूटन बले वह बल है जो 1 किग्रा द्रव्यमान को किसी वस्तु पर लगाए जाने पर उसमें 1 मी/से² का त्वरण उत्पन्न कर दे।

प्रश्न 2.
बल के मात्रक क्या हैं?
उत्तर :
न्यूटन, किग्रा-मी/से², किग्रा-भार, डाइन, ग्राम-सेमी/से2, ग्राम-भार।

प्रश्न 3.
बल के मात्रक को मूल मात्रकों में व्यक्त कीजिए।
उत्तर :
1 न्यूटन = 1 किग्रा-मी/से ², 1 डाइन = 1 ग्राम-सेमी/से²।

प्रश्न 4.
बल तथा त्वरण में क्या सम्बन्ध है?
उत्तर :
बल (F) ∝ त्वरण (a), अत: F = ma, जहाँ m वस्तु को.द्रव्यमान है जिस पर बल F.ने त्वरण उत्पन्न किया है।

प्रश्न 5.
जड़त्व की परिभाषा दीजिए।
उत्तर :
पदार्थ का वह गुण जो पदार्थ की अवस्था परिवर्तन का विरोध करता है, जड़त्व कहलाता है।

प्रश्न 6.
एक कार एवं बस में से किसका जड़त्व अधिक होगा?
उत्तर :
बस का द्रव्यमान कार से अधिक होती है; अत: बस का जड़त्वे भी अधिक होगा।

प्रश्न 7.
एक पिण्ड का द्रव्यमान m तथा वेग υ है, तो उसको संवेग बताइए
उत्तर :
p = mυ

प्रश्न 8.
बल तथा संवेग-परिवर्तन की दर में क्या सम्बन्ध है?
उत्तर :

प्रश्न 9.
आवेग से क्या तात्पर्य है?
उत्तर :
यदि कोई बल किसी वस्तु पर थोड़े समय के लिए कार्य करता है तो बल और उसके लगने के समय के गुणनफल को बल का आवेग कहते हैं। आवेग एक सदिश राशि है। S.I. पद्धति में आवेग को मात्रक न्यूटन-सेकण्ड होता है।

प्रश्न 10.
रॉकेट का क्रिया-सिद्धान्त गति के किस नियम पर आधारित है?
उत्तर :
गति के तृतीय नियम (क्रिया-प्रतिक्रिया के नियम) पर।

प्रश्न 11.
क्या क्रिया एवं प्रतिक्रिया बल एक ही वस्तु पर कार्य करते हैं अथवा अलग-अलग वस्तुओं पर?
उत्तर :
अलग-अलग वस्तुओं पर।

प्रश्न 12.
संगामी बलों से क्या तात्पर्य है?
उत्तर :
जब एक ही बिन्दु पर दो या दो से अधिक बल कार्य करते हैं तथा इस उभयनिष्ठ बिन्दु पर इन बलों का सदिश योग शून्य होता है, संगामी बल कहलाते हैं।

लघु उत्तरीय प्रश्न

प्रश्न 1.
जड़त्व से क्या तात्पर्य है? गति जड़त्व को उदाहरण सहित समझाइए।
उत्तर :
किसी पिण्ड का वह गुण जिसके कारण पिण्ड अपनी विरामावस्था में अथवा एकसमान गति की अवस्था में किसी भी प्रकार के परिवर्तन का विरोध करता है, जड़त्व कहलाता है। गति जड़त्व किसी वस्तु में उसकी गति अवस्था में परिवर्तन के विरोध का गुण गति जड़त्व कहलाता है। उदाहरण—चलती रेल में गेंद को ऊपर उछालने पर गेंद उछालने वाले के हाथ में वापस लौट आती है।

प्रश्न 2.
न्यूटन का गति विषयक प्रथम नियम लिखिए।
उत्तर :
न्यूटन का गति विषयक प्रथम नियम- इस नियम के अनुसार, ‘यदि कोई वस्तु विरामावस्था में है, तो वह विरामावस्था में ही रहेगी अथवा यदि कोई वस्तु गतिमान है, तो वह सरल रेखा में एकसमान वेग से ही गति करती रहेगी जब तक कि उस पर कोई बाह्य बल न लगाया जाए” इसे जड़त्व का नियम भी कहते हैं।

प्रश्न 3.
स्पष्ट कीजिए कि न्यूटन के गति विषयक द्वितीय नियम F =ma में उसका प्रथम नियम भी निहित है।
उत्तर :
न्यूटन के गति के द्वितीय नियम से, $\xrightarrow { F }$ = $\xrightarrow { ma }$

यदि $\xrightarrow { F }$ = 0 हो, तो $\xrightarrow { a }$ = 0 अर्थात् यदि वस्तु पर बाह्य बल ने लगाया जाए, तो वस्तु में त्वरण भी उत्पन्न नहीं होगा। त्वरण के शून्य होने पर या तो वस्तु विरामावस्था में ही रहेगी या एकसमान वेग से गतिमान रहेगी। यही न्यूटन का गति विषयके प्रथम नियम है; अत: न्यूटन के गति के द्वितीय नियम में प्रथम नियम स्वत: निहित है।

प्रश्न 4.
निम्नलिखित के कारण स्पष्ट कीजिए –
(i) तेज चलती गाड़ी से अचानक नीचे उतरने पर यात्री क्यों गिर पड़ता है?
(ii) पेड़ के हिलाने पर उसके फल टूट्टकर क्यों गिर जाते हैं?
(iii) बन्दूक से गोली चलाने पर पीछे की ओर धक्का लगता है, क्यों?
(iv) कुएँ से जल खींचते समय रस्सी टूट जाने पर हम पीछे की ओर गिर जाते हैं, क्यों?
उत्तर :

(i) तेज चलती गाड़ी से अचानक नीचे उतरने पर यात्री गिर पड़ता है – गाड़ी से उतरने से पूर्व यात्री के सम्पूर्ण शरीर का वेग गाड़ी के वेग के बराबर होता है। जैसे ही यात्री प्लेटफॉर्म पर या नीचे उतरता है, तो उसके पैर तो विरामावस्था में आ जाते हैं, परन्तु उसके शरीर का ऊपरी भाग गति जड़त्व के कारण उसी वेग से चलने का प्रयत्न करता है। अत: यात्री गाड़ी के चलने की दिशा में गिर पड़ता है। इसलिए चलती गाड़ी से उतरने पर कुछ दूर गाड़ी की दिशा में अवश्य दौड़ना चाहिए।

(ii) पेड़ की डाल हिलाने पर फल नीचे गिर पड़ते हैं – डाल हिलाने से पेड़ की डाल में यकायक गति उत्पन्न हो जाती है, परन्तु डाल पर लगे फल विराम जड़त्व के कारण अपने ही स्थान पर या नीचे रहने का प्रयत्न करते हैं। इस प्रकार फल डालियों से अलग हो जाते हैं और पृथ्वी के गुरुत्व-बल के कारण वे नीचे गिर पड़ते हैं।

(iii) बन्दूक से गोली चलाने पर पीछे की ओर धक्का लगता है – बन्दूक चलाने पर बारूद जलकर गैस बन जाती है, जो किं फैलने पर गोली को आगे की ओर फेंकती है। गोली जितने बल . से आगे फेंकी जाती है, बन्दूक पर प्रतिक्रिया बल भी उतना ही अधिक लगता है जिससे चलाने वाले को पीछे की ओर धक्का लगता है।

(iv) कुएँ से पानी खींचते समय रस्सी टूट जाने पर हम पीछे को गिर जाते हैं – इसका कारण यह है कि पहले मनुष्य रस्सी को अपनी ओर खींच रहा था। रस्सी टूट जाने पर रस्सी द्वारा मनुष्य पर लगने वाला बल लुप्त हो गया। अतः खिंचाव हट जाने के कारण वह गिर पड़ता है। बाल्टी जितनी अधिक भारी होती है उतनी ही अधिक शक्ति को धक्का हमें पीछे की ओर लगता है।

प्रश्न 5.
बल के आवेग और संवेग-परिवर्तन में सम्बन्ध स्थापित कीजिए।
या
सिद्ध कीजिए कि बल का आवेग, संवेग-परिवर्तन के बराबर होता है।
उत्तर :

प्रश्न 6.
एक पिण्ड का संवेग दो मिनट में 150 किग्रा-मी/से से बढ़कर 600 किग्रा-मी/से हो जाता है। पिण्ड पर आरोपित बल ज्ञात कीजिए।
हल :
प्रारम्भिक संवेग, p₁ = 150 किग्रा-मी/से
अन्तिम संवेग, p₂ = 600 किग्रा-मी/से
समय, t =2 मिनट = 120 सेकण्ड
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 56

प्रश्न 7.
20 ग्राम की एक वस्तु पर एक बल बहुत कम समय के लिए कार्य करता है, जिससे वस्तु का वेग शून्य से बढ़कर 10 मीटर/सेकण्ड हो जाता है। बल का आवेग ज्ञात कीजिए।
हल :
वस्तु को द्रव्यमान, m = 20 ग्राम = 20 × 10^-3 किग्रा
प्रारम्भिक वेग, u = 0
अन्तिम वेग, υ = 10 मीटर/सेकण्ड
प्रारम्भिक संवेग, p₁ = mu =20 × 10^-3 × 0 = 0
अन्तिम संवेग, P₂ = mυ =20 × 10^-3 × 10
=20 × 10^-2 न्यूटन-सेकण्ड
बल का आवेग = संवेग-परिवर्तन
= p₂– p₁
=20 × 10 ^-2 – 0 =20 × 10^-2
= 0.2 न्यूटन-सेकण्ड

प्रश्न 8.
दिए गए बल-समय वक़ से आवेग का परिमाण ज्ञात कीजिए।

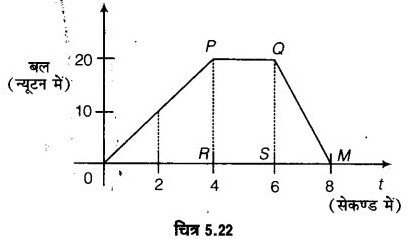
हल :
∵ प्रश्न में दिए चित्रानुसार,
∆ORP का क्षेत्रफल =1/2 × 4 × 20 = 40
∆MSQ का क्षेत्रफल =1/2 × 2 × 20 = 20
आयत PQRS का क्षेत्रफल = 2 × 20 = 40
आवेग का परिमाण = 40 + 20 + 40
= 100 न्यूटन – सेकण्ड

विस्तृत उत्तरीय प्रश्न

प्रश्न 1.
न्यूटन के गति का द्वितीय नियम लिखिए और व्याख्या कीजिए। इससे सम्बन्ध F = ma प्राप्त कीजिए जहाँ प्रतीकों के सामान्य अर्थ हैं।
या
यदि नियत द्रव्यमान m का कोई पिण्ड त्वरण $\xrightarrow { a }$ से गति कर रहा है तो सिद्ध कीजिए कि इस पिण्ड के लिए गति के द्वितीय नियम का रूप है $\xrightarrow { f }$ m $\xrightarrow { a }$ होगा। इस सूत्र के आधार पर बल के मापन की विधि समझाइए।
उत्तर :
न्यूटन का गति विषयक द्वितीय नियम – न्यूटन को गति का द्वितीय नियम, वस्तु के संवेग में परिवर्तन और उस पर आरोपित बाह्य बल के मध्य सम्बन्ध स्थापित करता है। इस नियम के अनुसार,
“किसी वस्तु के संवेग-परिवर्तन की दर उस पर आरोपित बाह्य बल के समानुपाती होती है तथा संवेग-परिवर्तन बल की दिशा में ही होता है।”
माना m द्रव्यमान की वस्तु पर कोई बल F, ∆ t समय तक कार्य करता है। यदि इसका वेग υ से υ + A) हो जाता है, तब इसके प्रारम्भिक संवेग p (= mυ) में ∆p (= m∆v) मान का संवेग-परिवर्तन हो जाता है।

अर्थात्

बल = द्रव्यमान × त्वरण

बल के s.I. मात्रक की परिभाषा
S.I. मात्रक में एकांक बल वह बल है जो 1 kg द्रव्यमान की वस्तु पर लगाकर उसमें 1 मी/से² का त्वरण उत्पन्न कर दे। इसे 1 न्यूटन (N) कहते हैं।
अतः 1 न्यूटन =1 किग्रा × 1 मी/से ² =1 किग्रा-मी-से ²

बल के मापन की विधि
सूत्र = $\xrightarrow { F }$ m $\xrightarrow { a }$ का अदिश रूप लेने पर,
F = ma
इस सूत्र में स्पष्ट है कि किसी दिए गए बल को मापन उस बल को एक ज्ञात द्रव्यमान के पिण्ड पर आरोपित करके उसमें उत्पन्न होने वाले त्वरण को मापकर किया जा सकता है।

प्रश्न 2.
संवेग की परिभाषा दीजिए। संवेग का दैनिक जीवन में महत्त्व लिखिए।
उत्तर :
संवेग – संवेग वह राशि है जो गतिशील वस्तु के वेग व द्रव्यमान दोनों पर निर्भर करती है। किसी वस्तु का संवेग वस्तु के द्रव्यमान और वेग के गुणनफल के बराबर होता है।
संवेग = द्रव्यमान × वेग
यदि किसी वस्तु का द्रव्यमान m एवं उसका वेग υ हो, तो वस्तु का रेखीय संवेग,
$\xrightarrow { p }$ = m x $\xrightarrow { v }$
संवेग एक सदिश (vector) राशि है। उसका मात्रक किग्रा-मी/से या न्यूटन-सेकण्ड होता है।
संवेग का दैनिक जीवन में महत्त्व – संवेग का दैनिक जीवन में महत्त्व निम्नलिखित है –

1. यदि दो वस्तुएँ समान वेग से गति कर रही हैं तो भारी (heavy) वस्तु का संवेग, हल्की (light) वस्तु के संवेग से अधिक होता है।
माना भारी वस्तु का द्रव्यमान M और हल्की वस्तु का द्रव्यमान m है तथा दोनों का वेग υ समान है
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 59
इससे स्पष्ट है कि यदि दो वस्तुएँ समान वेग से चल रही हैं तो भारी वस्तु का संवेग हल्की वस्तु के संवेग से अधिक होता है। यदि एक बस और एक दो पहिया स्कूटर समान वेग से चल रहे हों तो बस का संवेग स्कूटर के संवेग से बहुत अधिक होगा।

2. यदि दो वस्तुओं का संवेग बराबर है तो हल्की वस्तु का वेग भारी वस्तु के वेग से अधिक होगा।
माना भारी वस्तु का द्रव्यमान M तथा वेग V है और हल्की वस्तु का द्रव्यमान m तथा वेग υ है। चूंकि दोनों का संवेग बराबर है, अर्थात्
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 60

स्पष्ट है कि यदि दो वस्तुओं का संवेग एकसमान है तो हल्की वस्तु का वेग भारी वस्तु के वेग से अधिक होता है।

प्रश्न 3.
संवेग किसे कहते हैं? यह कैसी राशि है? संवेग का बल के साथ क्या सम्बन्ध है?
उत्तर :
संवेग – किसी वस्तु का संवेग वस्तु के द्रव्यमान तथा उसके वेग के गुणनफल के बराबर होता है। इसे $\xrightarrow { p }$ से प्रदर्शित करते हैं।
यदि किसी वस्तु का द्रव्यमान m तथा वेग $\overrightarrow { \nu }$ हो, तब उस वस्तु का संवेग
$\xrightarrow { p }$ = m $\overrightarrow { \nu }$
संवेग का S.I. मात्रक किग्रा-मीटर/सेकण्ड’ तथा C.G.S. मात्रक ‘ग्राम-सेमी/सेकण्ड’ है। यह एक सदिश राशि है तथा इसकी दिशा वस्तु के वेग की दिशा में होती है। इसका विमीय सूत्र [MLT-1] है।
बल व संवेग के बीच सम्बन्ध – इस नियम के अनुसार, “किसी वस्तु के संवेग परिवर्तन की दर, उस वस्तु पर आरोपित नेट बाह्य बल के अनुक्रमानुपाती होती है तथा बाह्य बल की दिशा में होती है।”
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 61

प्रश्न 4.
संवेग-संरक्षण का नियम लिखिए तथा इसे n पिण्डों के किसी निकाय के लिए सिद्ध कीजिए।
उत्तर :
संवेग-संरक्षण का नियम – इस नियम के अनुसार, “यदि पिण्डों के किसी निकाय पर नेट बाह्य बल शून्य है तब निकाय का संवेग नियत रहता है।”

प्रश्न 5.
संवेग संरक्षण सिद्धान्त लिखिए। इस सिद्धान्त के आधार पर न्यूटन के गति के तृतीय नियम को प्राप्त कीजिए।
उत्तर :
संवेग संरक्षण सिद्धान्त – इस सिद्धान्त के अनुसार, बाह्य बल की अनुपस्थिति में किसी। निकाय का सम्पूर्ण संवेग संरक्षित रहता है तथा समय के साथ इसमें कोई परिवर्तन नहीं होता।
$\xrightarrow { p }$ = नियतांक

संवेग संरक्षण सिद्धान्त से न्यूटन के गति विषयक तृतीय नियम का निगमन – माना कि दो पिण्ड परस्पर एक-दूसरे से टकराते हैं। टकराते समय वे एक-दूसरे पर बल लगाते हैं। माना कि पहले पिण्ड पर लगने वाला बल $\overrightarrow { F12 }$ है तथा दूसरे पर $\overrightarrow { F21 }$ है। माना कि इन बलों के कारण पहले व दूसरे पिण्डों में संवेग-परिवर्तन क्रमश: ∆ $\overrightarrow { P1 }$ व ∆ $\overrightarrow { P2 }$ हैं। यदि दोनों पिण्ड समयान्तराल ∆t तक एक-दूसरे के सम्पर्क में रहते हैं।

अर्थात् स्पष्ट है कि दो पिण्डों पर एक-दूसरे द्वारा लगाये गये बल बराबर तथा विपरीत दिशा में होते हैं। समीकरण का ऋणात्मक (-ve) चिह्न यह बताता है कि दोनों बल परस्पर विपरीत दिशाओं में कार्यरत हैं।

इस प्रकार हम कह सकते हैं कि एक पिण्ड की क्रिया दूसरे पिण्ड की प्रतिक्रिया के बराबर परन्तु विपरीत दिशा में होती है। यही न्यूटन को गति विषयक तृतीय नियम है।

प्रश्न 6.
बल के आवेग से क्या तात्पर्य है? यह सदिश राशि है अथवा अदिश? सिद्ध कीजिए कि किसी वस्तु पर बल को आवेग संगत समयान्तराल में वस्तु के संवेग में होने वाले परिवर्तन के बराबर होता है?
उत्तर :
बल का आवेग – जब कोई बहुत बड़ा बल अल्प समयावधि के लिए किसी वस्तु पर कार्य करके उस वस्तु के संवेग में पर्याप्त परिवर्तन उत्पन्न कर देता है तो ऐसे बल को आवेगी बल (Impulsive Force) कहते हैं तथा बल और समयावधि के गुणनफल को बल का आवेग (Impulse) कहते हैं तथा इसे $\xrightarrow { I }$ से प्रदर्शित करते हैं।

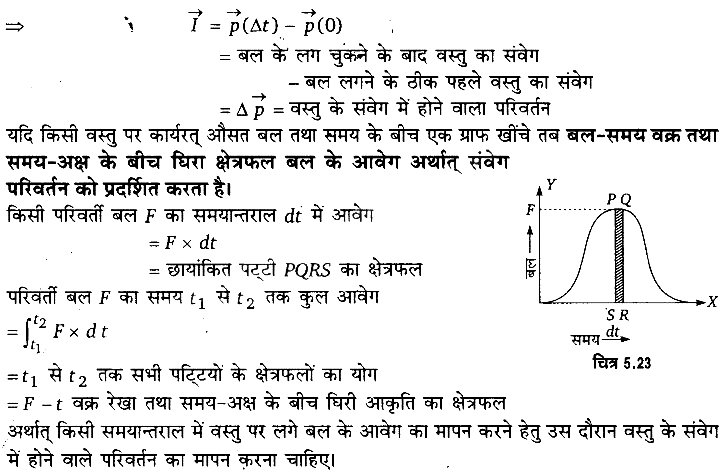
प्रश्न 7.
संगामी बलों (concurrent forces) से क्या तात्पर्य है? संगामी बलों के सन्तुलन की विवेचना कीजिए।
उत्तर :
संगामी बल – किसी एक ही बिन्दु पर क्रिया करने वाले बलों को कण संगामी बल कहते हैं।
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 66

संगामी बलों का सन्तुलन – यदि किसी एक बिन्दु पर लगे बलों का परिणामी बल शून्य है तो वे बल सन्तुलन में कहलाते हैं।
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 67

अर्थात् समान्तर चतुर्भुज के नियमानुसार प्राप्त किन्हीं दो बलों के परिणामी परिमाण में तीसरे बल के बराबर परन्तु दिशा में उसके विपरीत होना चाहिए।

ये समीकरण किसी बिन्दु पर लगे तीन बलों के सन्तुलन के प्रतिबन्धों को प्रदर्शित करते हैं। इन समीकरणों के आधार पर कहा जा सकता है कि किसी बिन्दु पर लगे तीन बल सन्तुलन में होंगे यदि और केवल यदि किन्हीं तीन परस्पर लम्बवत् दिशाओं में बलों के वियोजित घटकों के बीजीय योगफल अलग-अलग शून्य हों।

अतः स्पष्ट है कि यदि n समांगी बल साम्यावस्था में हैं, तब किन्हीं तीन परस्पर लम्बवत् दिशाओं में उनके घटकों का बीजीय योगफल शून्य होता है।

इस प्रकार, स्पष्ट है कि यदि किसी कण पर कार्यरत् संगामी बल साम्यावस्था में हैं तब कण की अवस्था में कोई परिवर्तन नहीं होता है, अर्थात् यदि ‘कण विराम में है तो वह विरामावस्था में ही बना रहता है और यदि एकसमान गति की अवस्था में है तो सरल रेखा में एकसमान गति करता रहता है।

प्रश्न 8.
2 किग्रा तथा3 किग्रा द्रव्यमान के दो पिण्ड, एक हल्की डोरी से चित्रानुसार लटके हुए हैं। डोरी घर्षणहीन घिरनी पर से होकर गुजरती है। यदि घिरनी 5 मी/से² के त्वरण से ऊपर उठाई जाती है, तो डोरी में तनाव बल की। गणना कीजिए। (g = 10 मी/से²)
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 71

प्रश्न 9.
0.3 किग्रा का एक पिण्ड छत से एक हल्की डोरी द्वारा लटकाया गया है। 0.7 किग्रा का दूसरा पिण्ड, प्रथम पिण्ड से दूसरी हल्की डोरी द्वारा लटकाया गया है। दोनों डोरियों में तनाव बलों का परिकलन कीजिए। (g= 10 ms^-2)
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 73

प्रश्न 10.
x-अक्ष के अनुदिश 3 मी/से के वेग से गतिशील m द्रव्यमान की एक गेंद, 2m द्रव्यमान की दूसरी स्थिर गेंद से टकराती है। टक्कर के बाद पहली गेंद स्थिर हो जाती है तथा दूसरी गेंद एकसमान द्रव्यमान के दो टुकड़ों में विभक्त हो जाती है। यदि एक टुकड़ा 3 मी/से के वेग से Y-अक्ष के अनुदिश गति प्रारम्भ करता है, तो दूसरे भाग का वेग तथा गति की दिशा क्या होगी?

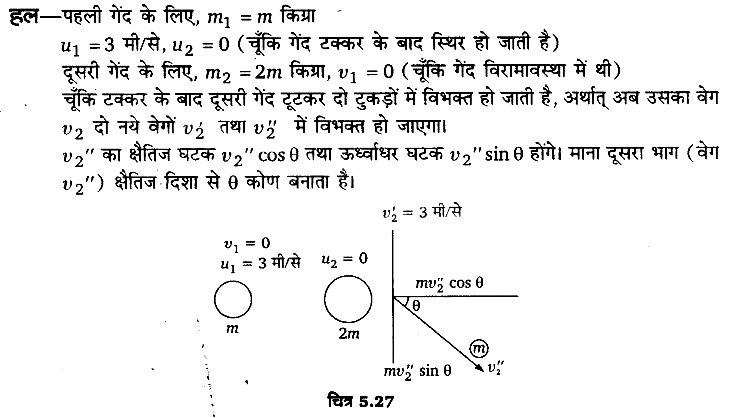
प्रश्न 11.
चित्र 5.28 के अनुसार ब्लॉक A पर एक नियत बल F = 0.1 किग्रा-भार को लगाया है। पुली तथा डोरी नगण्य भार की है तथा मेज की सतह चिकनी है। ब्लॉक A का त्वरण ज्ञात कीजिए। प्रत्येक ब्लॉक का द्रव्यमान 0.2 किग्रा है।
UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion 77

We hope the UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion (गति के नियम) help you.

UP Board Solutions for Class 11 Physics Chapter 5 Laws of motion (गति के नियम)

Leave a Reply Cancel reply