UP Board Solutions for Class 11 Psychology Chapter 12 Statistics in Psychology (मनोविज्ञान में सांख्यिकीय गणना)

UP Board Solutions for Class 11 Psychology Chapter 12 Statistics in Psychology (मनोविज्ञान में सांख्यिकीय गणना)

UP Board Solutions for Class 11 Psychology Chapter 12 Statistics in Psychology (मनोविज्ञान में सांख्यिकीय गणना)

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
सांख्यिकी का अर्थ स्पष्ट कीजिए। सांख्यिकी को परिभाषित कीजिए।
या
सांख्यिकी से आप क्या समझते हैं? इसे परिभाषित करते हुए बताइए कि आप किस परिभाषा को उपयुक्त समझते हैं और क्यों?
या
“सांख्यिकी गणना का विज्ञान है।’ इस कथन की व्याख्या करते हुए समझाइए कि आपकी दृष्टि में सांख्यिकी की सही परिभाषा क्या होनी चाहिए?

उत्तर :

सांख्यिकी का अर्थ एवं परिभाषा
(Meaning and Definition of Statistics)

‘सांख्यिकी अंग्रेजी शब्द ‘स्टैटिस्टिक्स (Statistics) का हिन्दी रूपान्तर है। अंग्रेजी भाषा का स्टैटिस्टिक्स (Statistics) शब्द लैटिन भाषा के ‘स्टेटस (Status), इटैलियन भाषा के ‘स्टैटिस्टा (Statista) या जर्मन भाषा के स्टैटिस्टिक’ (Statistik) शब्द से उत्पन्न हुआ है। इन सभी शब्दों का अर्थ राज्य (State) होता है। इस प्रकार प्रारम्भ में सांख्यिकी का प्रयोग राज्य विज्ञान के रूप में किया जता था। वास्तविक रूप में सांख्यिकी’ शब्द का प्रयोग करने का श्रेय जर्मन विद्वान् गॉटफ्रायड एकेनॉल (Gottfried Achenwall) को जाता है। उन्होंने 1749 ई० में सांख्यिकी को मानव ज्ञान की एक विशिष्ट शाखा के रूप में प्रयोग किया।

सांख्यिकी’ (Statistics) शब्द का दो अर्थों में प्रयोग होता है—एक ‘एकवचन’ में तथा दूसरा ‘बहुवचन’ में। एकवचन के अर्थ में ‘सांख्यिकी’ का प्रयोग एक विज्ञान के रूप में किया जाता है। बहुवचन के अर्थ में ‘सांख्यिकी का प्रयोग आँकड़ों, संख्याओं या समंकों के रूप में लिया जाता है।

अब हम ‘सांख्यिकी’ (Statistics) शब्द की परिभाषा का उपर्युक्त दोनों ही अर्थों में अध्ययन करेंगे।

बहुवचन के रूप में सांख्यिकी का अर्थ एवं परिभाषाएँ

बहुवचन के रूप में ‘साख्यिकी’ शब्द का अर्थ समंकों या आँकड़ों से है जो किसी विशिष्ट क्षेत्र से सम्बन्धित संख्यात्मक तथ्य होते हैं। जनसंख्या, शिक्षा, कृषि, स्त्री-शिक्षा, प्रौढ़-शिक्षा आदि से सम्बन्धित आँकड़े बहुवचन के रूप में होते हैं।

(1) गॉटफ्रायड एकेनवाल के अनुसार, “राज्य से सम्बन्धित ऐतिहासिक और विवरणात्मक महत्त्वपूर्ण तथ्यों का संग्रह ‘समंक’ है।”

(2) डॉ० ए० एल० बाउले के अनुसार, “किसी अनुसन्धान से सम्बन्धित तथ्यों का अंकात्मक विवरण ‘समंक’ होते हैं, जिन्हें एक-दूसरे के सम्बन्ध में रखा जा सकता है।”

(3) होरेस सेक्राइस्ट के अनुसार, “सांख्यिकी से हमारा तात्पर्य तथ्यों के उन समूहों से है जो अनेक कारणों से पर्याप्त सीमा तक प्रभावित होते हैं, जो संख्यात्मक रूप से व्यक्त किये जाते हैं, जिनकी गणना या अनुमान शुद्धता के एक उचित स्तर तक की जाती है तथा जिन्हें किसी पूर्व निश्चित उद्देश्य की पूर्ति के लिए क्रमबद्ध ढंग से संगृहीत किया जाता है तथा जिन्हें एक-दूसरे से सम्बन्धित करके रखा जाता है।”

उपर्युक्त परिभाषाओं में होरेस सेक्राइस्ट की परिभाषा ही सर्वश्रेष्ठ है। इस परिभाषा में समंकों की सभी विशेषताओं पर पूर्ण प्रकाश डाला गया है।

एकवचन अर्थात् विज्ञान के रूप में सांख्यिकी की परिभाषाएँ

एकवचन के रूप में ‘सांख्यिकी’ शब्द का प्रयोग एक विज्ञान की दृष्टि से किया जाता है। सांख्यिकी विज्ञान की परिभाषाओं को तीन भागों में विभक्त किया गया है –

(क) संकुचित परिभाषाएँ

प्रारम्भ में सांख्यिकी को एक राज्य-विषय के रूप में जाना जाता था; अतः प्राचीन परिभाषाएँ सांख्यिकी के केवल कुछ पहलुओं पर प्रकाश डालती है जो कि निम्नलिखित हैं

(1) बॉडिंगटन (Boddington) के अनुसार, “सांख्यिकी अनुमानों और सम्भावनाओं का विज्ञान है।” बॉडिंगटन की परिभाषा में सांख्यिकी के क्षेत्र को संकुचित कर दिया गया है। इन्होंने इसे केवल विज्ञान माना है, न कि विज्ञान और कला दोनों।

(2) डॉ० बाउले ने सांख्यिकी की तीन परिभाषाएँ दी हैं –

(i) “सांख्यिकी गणना का विज्ञान है।”
उपर्युक्त परिभाषा में सांख्यिकीय अनुसन्धान की अनेक विधियों में से केवल गणना विधि को महत्त्व दिया गया है, किन्तु केवल गणना ही सांख्यिकीय नहीं है। विशाल संख्याओं का तो मात्र अनुमान लगाया जाता है, उनकी गणना नहीं की जाती; अतः यह परिभाषा अधूरी है।

(ii) “सांख्यिकी को सही रूप में औसतों को विज्ञान कहा जा सकता है।”
प्रस्तुत परिभाषा में औसत पर बल दिया गया है। सांख्यिकीय विश्लेषण में न केवल औसत (मध्य) का प्रयोग होता है अपितु अपकिरण, विषमता, सह-सम्बन्धन आदि का भी प्रयोग किया जाता है; अतः यह परिभाषा भी अधूरी है।

(iii) “सांख्यिकी, सामाजिक व्यवस्था को सम्पूर्ण मानकर माप का विज्ञान है।”
डॉ० बाउले ने इस परिभाषा में सांख्यिकी को केवल सामाजिक संस्थाओं एवं उनके क्रिया-व्यवहार के मापन का विज्ञान कहा है। इस प्रकार गैर सामाजिक क्रियाएँ सांख्यिकी के क्षेत्र से बाहर कर सांख्यिकी का क्षेत्र अति संकुचित बना दिया गया है।

(3) पर्सन और हार्लोज के शब्दों में, “सांख्यिकी तथ्यों के समूह को प्रयोग में लाने का विज्ञान और कला है।”

प्रस्तुत परिभाषा में विश्लेषण की विधियों को स्पष्ट नहीं किया गया है।

(ख) विस्तृत परिभाषाएँ

(1) क्रॉक्स्टन और काउडेन के अनुसार, “सांख्यिकी को संख्यात्मक, समंकों के एकत्रीकरण, प्रस्तुतीकरण, विश्लेषण तथा निर्वचन के रूप में परिभाषित किया जा सकता है।”

(2) प्रो० सैलिगमैन के अनुसार, “सांख्यिकी वह विज्ञान है जो किसी भी अनुसन्धान (जाँच) के क्षेत्र पर प्रकाश डालने के लिए संख्यात्मक आँकड़ों के संग्रहण, प्रस्तुतीकरण, वर्गीकरण, तुलना तथा निर्वचन की रीतियों का प्रयोग करता है।”

(3) लाविट के अनुसार, “सांख्यिकी वह विज्ञान है जो संख्यात्मक तथ्यों के संग्रह, वर्गीकरण तथा सारणीयन से सम्बन्ध रखता है जिसे घटनाओं की व्याख्या, विवरण और तुलना के लिए प्रयुक्त किया जा सके।

उपर्युक्त परिभाषाओं की निम्नलिखित विशेषताएँ हैं –

1. सांख्यिकी की प्रकृति को स्पष्ट करें
2. सांख्यिकी के उद्देश्य को स्पष्ट करें
3. सांख्यिकी के विषय-क्षेत्र को स्पष्ट करें तथा
4. सांख्यिकी, विज्ञान और कला दोनों है।

(ग) उपयुक्त परिभाषा

सांख्यिकी की उपयुक्त परिभाषा वही हो सकती है जिसमें निम्नलिखित विशेषताएँ हों –

1. सांख्यिकी की प्रकृति को स्पष्ट करे
2. सांख्यिकी के उद्देश्य को स्ट करे
3. सांख्यिकी के विषय-क्षेत्र को स्पष्ट करे तथा
4. सांख्यिकी की विभिन्न रीतियों को स्पष्ट करे।

अन्त में हम कह सकते हैं कि सांख्यिकी, विज्ञान एवं कला दोनों ही है जिसमें पूर्व-निश्चित उद्देश्यों के अनुसार सर्वेक्षणों, अध्ययनों एवं प्रयोगों आदि के आधार पर प्राप्त आँकड़ों का संकलन, वर्गीकरण, विवरण, विश्लेषण, तुलना एवं विवेचन किया जाता है। आँकड़ों के विश्लेषण को उद्देश्यों, तथ्यों के पारस्परिक सम्बन्ध को ज्ञात करना, तथ्यों की विशेषताओं को वर्णन करना, तथ्यों के सम्बन्ध में अनुमान लगाना, निष्कर्ष निकालना और भविष्य कथन करना है।

प्रश्न 2.
सांख्यिकी की प्रकृति स्पष्ट कीजिए।
या
सांख्यिकी विज्ञान है अथवा कला। स्पष्ट कीजिए।
या
सांख्यिकी विज्ञान एवं कला दोनों ही है।” स्पष्ट कीजिए।
या
सांख्यिकी एक विज्ञान नहीं है, वह एक वैज्ञानिक विधि है।” आलोचनात्मक विवेचना कीजिए।
उत्तर :
सांख्यिकी की प्रकृति
(Nature of Statistics)

सांख्यिकी की प्रकृति या स्वभाव जानने के लिए यह देखना होगा कि सांख्यिकी विज्ञान है या कला अथवा दोनों है। अत: सर्वप्रथम हमें विज्ञान और कला का अर्थ जानना जरूरी है।

विज्ञान का अर्थ (Meaning of Science) – विज्ञान, ज्ञान के क्रमबद्ध समूह को कहते हैं। साधारणत: निम्नलिखित शर्तों को पूर्ण करने वाले ज्ञान (विषय) को विज्ञान कह सकते हैं –

1. जिस ज्ञान का क्रमबद्ध अध्ययन (Systematic Study) किया जाता हो।
2. वह ज्ञाप्त जिससे कारण और प्रभाव (Cause and Effect) के सम्बन्धों की जानकारी मिलती है।
3. जिस ज्ञान के अध्ययन के लिए स्वयं के नियम होते हैं।
4. जिसके नियम सार्वभौमिक (Universal) होते हैं।
5. जिसके नियमों के द्वारा भविष्यवाणी या पूर्वानुमान (Forecasting) किये जा सके।
6. जिसका अन्य विज्ञानों से सम्बन्ध होता है।

कला का अर्थ (Meaning of Art)-यदि विज्ञान ज्ञान है तो कला क्रिया है। किसी कार्य को करना ही कला कहलाता है। कला विज्ञान का व्यावहारिक या प्रयोगात्मक पहलू (Practical Aspect) है। किसी विज्ञान के विभिन्न नियमों तथा सिद्धान्तों का प्रयोग और क्रियान्वयन ही कला कहलाता है।

‘विज्ञान’ और ‘कला’ का अर्थ समझने के बाद अब हमें यह देखना है कि सांख्यिकी विज्ञान है। या कला है अथवा दोनों।

सांख्यिकी एक विज्ञान के रूप में
(Statistics as a Science)

सांख्यिकी एक विज्ञान है, क्योंकि इसमें विज्ञान के ऊपर वर्णित सभी लक्षण या विशेषताएँ पायी जाती हैं। सांख्यिकी ज्ञान का क्रमबद्ध अध्ययन करती है। अध्ययन के लिए इसके अपने स्वयं के सिद्धान्त और पद्धतियाँ हैं। इसके अपने नियम हैं; जैसे—सम्भावना का नियम, जड़ता का नियम, सांख्यिकीय नियमितता का नियम आदि। ये नियम सार्वभौमिक तथा सार्वकालिक हैं। इन नियमों के द्वारा अध्ययन करके पुर्वानुमान या भविष्यवाणी की जा सकती है। सांख्यिकी में ‘कारण’ और ‘प्रभाव (Cause and Effect) में सम्बन्ध स्थापित करने की क्षमता है। सांख्यिकी के नियमों द्वारा किसी ‘कारण’ के ‘परिणाम’ का विश्लेषण और पूर्वानुमान लगाया जा सकता है। इस प्रकार यह कहा जा सकता है कि सांख्यिकी एक विज्ञान है। इसमें विज्ञान होने के सभी लक्षण पाये जाते हैं।

सांख्यिकी एक कला के रूप में
(Statistics as an ‘Art’)

सांख्यिकी कला भी है। यह विभिन्न समस्याओं के समाधान की विधि बताती है। सांख्यिकीय समंकों को एकत्रित करना, उनका उपयोग करना आदि कला के स्वरूप को व्यक्त करते हैं। विभिन्न वर्गों पर मूल्यवृद्धि का जो प्रभाव पड़ता है, उसकी जानकारी मूल्य-निर्देशकों (Price Index) द्वारा की जाती है। यह सांख्यिकी का कला पक्ष ही है। सामाजिक, आर्थिक, राजनीतिक समस्याओं का विभिन्न सांख्यिकीय विधियों से अध्ययन करके आँकड़ों को बिन्दुरेखाओं (Graphs), चित्रों (Diagrams) एवं तालिकाओं द्वारा प्रदर्शित करना भी कला ही है। सांख्यिकी की विषय-वस्तु (Subject-matter) में व्यावहारिक सांख्यिकी का समावेश है।

विभिन्न सांख्यिकीय तथ्यों को तुलनीय बनाना तथा उनसे निष्कर्ष निकालना सांख्यिकी के कला पक्ष को स्पष्ट करते हैं।

सांख्यिकी विज्ञान और कला दोनों है।

उपर्युक्त विवेचन से यह स्पष्ट है कि सांख्यिकी न केवल विज्ञान है, अपितु कला भी है। यह सैद्धान्तिक तथा व्यावहारिक दोनों प्रकार का विज्ञान है। अन्त में टिप्पेट के शब्दों में कह सकते हैं, सांख्यिकी विज्ञान और कला दोनों है। यह विज्ञान इसलिए है क्योंकि इसकी रीतियाँ मौलिक रूप से क्रमबद्ध हैं तथा उनका सर्वत्र उपयोग होता है और कला इसलिए है कि इसकी रीतियों का सफल प्रयोग पर्याप्त सीमा तक सांख्यिकी की योग्यता, विशेष अनुभव तथा उसके प्रयोग-क्षेत्र; जैसे—अर्थशास्त्र के ज्ञान पर निर्भर करता है।”

अन्त में, सांख्यिकी एक विज्ञान और कला दोनों है जिसमें किसी अनुसन्धान क्षेत्र से सम्बन्धित सामूहिक संख्यात्मके तथ्यों के संकलन, प्रदर्शन, विश्लेषण तथा निर्वचन की रीतियों का विधिवत् । अध्ययन किया जाता है।

सांख्यिकी एक वैज्ञानिक विधि है
(Statistics is a Scientific Method)

क्रॉक्सटन और काउडेन का यह विचार है कि सांख्यिकी स्वयं एक विज्ञान नहीं है, अपितु अनुसन्धान करने की एक वैज्ञानिक विधि है, ज्ञान-प्राप्ति का एक तरीका है। उपर्युक्त शीर्षकों के अन्तर्गत हम सांख्यिकी की प्रकृति को स्पष्ट करते हुए उल्लेख कर चुके हैं कि सांख्यिकी एक विज्ञान भी है और कला भी, परन्तु क्रॉक्सटन और काउडेन का मत भिन्न है। वे इसे विज्ञान नहीं मानते वरन् एक वैज्ञानिक विधि (तरीका) मानते हैं, क्योंकि सभी विषयों में अनुसन्धान के लिए सांख्यिकीय विधियों का प्रयोग भरपूर तरीके से किया जाता है। अनुसन्धानकर्ता अपने-अपने निष्कर्षों को सांख्यिकीय विधियों से प्रदर्शित करते हैं; प्राप्त आँकड़ों का वर्गीकरण व निर्वचन करते हैं। जीवन के सभी क्षेत्रों अर्थात् सामाजिक, आर्थिक, राजनीतिक, मनोवैज्ञानिक एवं प्राकृतिक क्षेत्रों में सांख्यिकीय विधियों का उपयोग किया जाता है। यही कारण है कि वॉलिस और रॉबर्स कहते हैं, “सांख्यिकी स्वतन्त्र और मूलभूत ज्ञान का समूह नहीं है, अपितु ज्ञान-प्राप्ति की रीतियों का समूह है।”

इस तरह इन विद्वानों के अनुसार, सांख्यिकी अर्थशास्त्र, भौतिकशास्त्र या रसायनशास्त्र आदि की तरह स्वयं एक स्वतन्त्र विशुद्ध विज्ञान नहीं है, अपितु ज्ञान-प्राप्ति की वैज्ञानिक विधि है। परन्तु अधिकांश विशेषज्ञ सांख्यिकी को एक विज्ञान मानते हैं; क्योंकि विज्ञान की सभी विशेषताएँ और लक्षण इसमें पाये जाते हैं।

प्रश्न 3.
मनोविज्ञान में सांख्यिकी की उपयोगिता प्रतिपादित कीजिए।
उत्तर :
आधुनिक समय में मानव-जीवन की सभी समस्याओं के अध्ययन तथा समाधान में सांख्यिकी की उपयोगिता है और जीवन के प्रत्येक मोड़ पर यह पथ-प्रदर्शक की तरह कार्य करती है। यही कारण है कि विद्वान् सांख्यिकी को ‘मानव-कल्याण का अंकगणित’ कहते हैं। वर्तमान में मानवजीवन का शायद ही कोई ऐसा क्षेत्र हो जिसमें सांख्यिकी का उपयोग एवं महत्त्व न हो। सांख्यिकी के बढ़ते हुए महत्त्व एवं उपयोगिता के कारण टिप्पट (Tippet) ने कहा है, “सांख्यिकी प्रत्येक व्यक्ति को ‘प्रभावित करती है तथा जीवन को अनेक बिन्दुओं पर स्पर्श करती है।”

सामाजिक विज्ञानों की भाँति, मनोविज्ञान में भी सांख्यिकी का उपयोग दिन-प्रतिदिन विस्तार ले। रहा है। मनोविज्ञान की समस्याओं को समझने तथा उनके समाधान के लिए और मनोविज्ञान से सम्बन्धित शोध-कार्यों में सांख्यिकी का उपयोग अपरिहार्य हो गया है। मनोविज्ञान में सांख्यिकी की उपयोगिता की निम्नलिखित प्रकार विवेचना कर सकते हैं

मनोविज्ञान में सांख्यिकी की उपयोगिता
(Utility of Statistics in Psychology)

मनोविज्ञान में सांख्यिकी की उपयोगिता निर्विवाद, सार्वभौमिक तथा सार्वकालिक है। प्रायः सभी मनोवैज्ञानिक अध्ययनों, प्रयोग एवं शोध कार्यों में सांख्यिकी की भारी माँग है। सच तो यह है कि सांख्यिकीय विधियों के अभाव में ये कार्य हो ही नहीं सकते। मनोविज्ञान के क्षेत्र में सांख्यिकी की उपयोगिता के निम्नलिखित कारण हैं –

(1) आँकड़ों को सरल एवं बोधगम्य बनाना – मनोवैज्ञानिक प्रयोग अक्सर एक विशाल समूह पर लागू किये जाते हैं जिनसे प्रदत्त या समंक आँकड़े प्राप्त होते हैं। इन आँकड़ों को सार्थक बनाने के लिए आवश्यक है कि इन्हें सुव्यवस्थित किया जाए आँकड़ों को सुव्यवस्थित बनाने में सांख्यिकी विधियाँ उपयोगी हैं। उदाहरण के लिए–आँकड़ों का आवृत्ति वितरण बनाकर उन्हें विभिन्न रेखाचित्रों द्वारा प्रदर्शित करने में सांख्यिकी का बहुत महत्त्व है। केन्द्रीय प्रवृत्ति के मापन की विधियों द्वारा आँकड़ों का वर्णन करने में भी सांख्यिकी उपयोगी है। इस भॉति, सांख्यिकी अव्यवस्थित एवं अर्थहीन आँकड़ों को सरल तथा बोधगम्य बनाती है।

(2) ऑकड़ों की सुस्पष्ट एवं संक्षिप्त प्रस्तुतीकरण – सांख्यिकी की मदद से मनोवैज्ञानिक अध्ययनों से सम्बद्ध आंकड़ों का सरल, सुस्पष्ट एवं संक्षिप्त प्रस्तुतीकरण किया जाता है। वृत्तचित्र, स्तम्भ रेखाचित्र, आवृत्ति बहुभुज, स्तम्भाकृति, संचित प्रतिशत वक्र तथा संचित आवृत्ति वक्र आदि विधियों के द्वारा आँकड़ों की मुख्य विशेषताओं को स्पष्टता मिलती है। एक मनोवैज्ञानिक बालकों के एक बड़े समूह पर बुद्धि परीक्षण का प्रयोग करके मध्यमान तथा प्रामाणिक विचलन की गणना द्वारा सभी इकाइयों में सामूहिक रूप से मिलने वाले लक्षणों को खोज निकालता है। वह बालकों की औसत बुद्धि ज्ञात कर सकता है और यह पता भी लगा सकता है कि समूह सजातीय है अथवा विषमजातीय। पढ़ने वाले बालकों की योग्यताओं में विषमता अधिक होने पर कक्षा को कई हिस्सों में विभाजित कर बालकों की योग्यताओं के अनुसार पढ़ाया जा सकता है। इसी प्रकार आँकड़ों के वर्णन में सामान्य सम्भावना वक्र के प्रारम्भिक सिद्धान्तों का उपयोग भी किया जाता है।

(3) आँकड़ों को मात्रात्मक स्वरूप प्रदान करना – अन्य सामाजिक विज्ञानों की तरह से मनोविज्ञान में शोध कार्य के अन्तर्गत प्राप्त आँकड़े प्रायः गुणात्मक प्रकृति के होते हैं जिन्हें मात्रात्मक स्वरूप प्रदान करना होता है। यह कार्य सांख्यिकीय विधियों की सहायता से ही सम्भव है। बुद्धि, समायोजन, अन्तर्मुखता, बहिर्मुखता आदि से सम्बन्धित गुणात्मक आँकड़ों को मात्रात्मक रूप में परिवर्तित करने के लिए सांख्यिकी अत्यन्त उपयोगी है।

(4) घटना की यथार्थ व्याख्या – सांख्यिकीय विधियाँ किसी घटना की यथार्थ व्याख्या (Exact descriptions) करने में सक्षम हैं। इस व्याख्या को कोई भी प्रशिक्षित व्यक्ति बिना किसी सन्देह के ठीक-ठीक समझ सकता है। यदि कहा जाए कि कक्षा 12 के छात्र श्याम ने मनोविज्ञान में बहुत अच्छे अंक प्राप्त किये हैं तो इससे श्याम की मनोविज्ञान में योग्यता का सुनिश्चित ज्ञान नहीं होता; किन्तु यदि यह कहा जाए कि श्याम के मनोविज्ञान में प्राप्तांकों का प्रतिशत 95 है तो इससे स्पष्टतया ज्ञात होता है। कि 95% छात्रों के मनोविज्ञान में प्राप्तांक, श्याम के प्राप्तांकों से कम हैं। इस भाँति सांख्यिकी की सहायता से घटना की सही-सही व्याख्या की जा सकती है।

(5) आँकड़ों के सहसम्बन्ध का वर्णन – मनोविज्ञान से जुड़े अध्ययन एवं अनुसन्धान कार्यों में सांख्यिकीय विधियों की सहायता से दो या दो से अधिक चरों (variables) में सहसम्बन्ध ज्ञात किया जा सकता है। यदि कोई मनोवैज्ञानिक किसी कक्षा के बालकों की आयु और उनकी स्मरण-शविन के मध्य सम्बन्ध ज्ञात करना चाहे तो वह सहसम्बन्ध गुणांक को प्रयोग करता है। सहसम्बन्ध की विधियाँ आंशिक तथा बहुगुणी सहसम्बन्ध की गणना भी कर सकती हैं।

(6) तुलनात्मक अध्ययन – बॉडिंगटन का कथन है, “सांख्यिकी का निचोड़ गणना करना ही नहीं है अपितु तुलना करना भी है।’ मनोवैज्ञानिक दो या दो से अधिक समूहों की तुलना के लिए सांख्यिकीय विधियों का प्रयोग कर सकते हैं। उदाहरण के लिए यदि यह ज्ञात करना हो कि कक्षा 11 के छात्रों को मनोविज्ञान पढ़ाने के लिए शिक्षण की पुस्तक-पाठन तथा व्याख्यान विधि में से कौन-सी विधि अच्छी है तो इसके लिए प्रयोग किया जा सकता है। समान योग्यता वाले छात्रों के दो समूह बनाकर एक समूह को पुस्तक-पाठन विधि द्वारा तथा दूसरे समूह को व्याख्यान विधि द्वारा पढ़ाया जाएगा। फिर दोनों समूहों की प्रामाणिक परीक्षा लेकर उनके प्राप्तांकों पर सांख्यिकीय विधियाँ लागू कर तुलनात्मक अध्ययन द्वारा यह बताना सम्भव है कि मनोविज्ञान शिक्षण की प्रभावशाली विधि कौन-सी

(7) कार्यकारण सम्बन्ध – सांख्यिकीय विधियों की सहायता से कोई भी मनोवैज्ञानिक किसी घटना को उत्पन्न करने वाले कारणों को ज्ञात कर सकता है। इसके लिए स्वतन्त्र चर का परतन्त्र चर पर पड़ने वाले प्रभाव का अध्ययन करना होगा। यदि यह ज्ञात करना हो कि अमुक छात्र किसी विषय में क्यों फेल हो जाता है तो तत्सम्बन्धी कारणों को प्रयोगात्मक विधि (Experimental Method) द्वारा ज्ञात किया जा सकता है। उदाहरणार्थ- प्रयोग में सभी कारणों को स्थिर (Constant) करने के उपरान्त यह पाया जाए कि नियमित अध्ययन न करने वाले छात्र फेल हो जाते हैं तो सम्भवतया छात्र के उस विषय में फेल होने का कारण, नियमित अध्ययन का अभाव ही हो।

(8) मापन तथा मनोवैज्ञानिक परीक्षणों में सांख्यिकी का उपयोग – सांख्यिकीय विधियों के अभाव में मनोवैज्ञानिक परीक्षणों का निर्माण, उनकी व्याख्या तथा विश्वसनीयता व वैधता की जाँच नहीं की जा सकती। बुद्धि-परीक्षण, निष्पत्ति परीक्षण, अभिवृत्ति परीक्षण तथा प्रवणता परीक्षण आदि के निर्माण में सांख्यिकीय विधियाँ अत्यधिक उपयोगी हैं। इसी प्रकार मनोवैज्ञानिक मापन में भी सांख्यिकी बहुत उपयोगी है।

(9) भविष्यकथन में सांख्यिकी का उपयोग – जब कोई मनोवैज्ञानिक मानव-व्यवहार से सम्बन्धित किसी घटना के सम्बन्ध में पूर्वानुमान लगाना चाहता है या भविष्यकथन करना चाहता है तो वह सांख्यिकी की प्रतीपगमन तथा भविष्यकथन से सम्बन्धित विधियों का उपयोग करता है। उदाहरण के लिए यदि कक्षा बारह के किसी छात्र की बुद्धि-लब्धि (I.Q.), हाईस्कूल में उसके प्राप्तांक तथा अध्ययन के घण्टों के आधार पर उसकी बोर्ड की परीक्षा में सफलता का पूर्वानुमान/भविष्यकथन करना हो तो प्रतीपगमन रेखाओं की मदद से ऐसा किया जा सकता है। मनोवैज्ञानिक सांख्यिकीय विधियों की सहायता से यह भी ज्ञात किया जा सकता है कि उसका भविष्यकथन कितना त्रुटिपूर्ण है।

(10) शैक्षिक समस्याओं का निदान – सांख्यिकीय विधियाँ शैक्षिक समस्याओं के निराकरण में भी विशिष्ट भूमिका निभाती हैं। छात्रों के चयन (Selection), उनकी पदोन्नति (Promotion) तथा शैक्षिक उपलब्धियों (Educational Achievements) के विषय में भविष्यकथन करने में भी सांख्यिकीय विधियाँ उपयोगी हैं। छात्रों के लिए परीक्षण तैयार करने व उनके मूल्यांकन में सांख्यिकी की महत्त्वपूर्ण भूमिका है। इसी प्रकार छात्रों के मार्गदर्शन में सांख्यिकीय विधियाँ अत्यन्त उपयोगी सिद्ध

उपर्युक्त विवेचन के आधार पर निष्कर्ष निकलता है कि मनोविज्ञान में सांख्यिकी की महती उपयोगिता है। मनोवैज्ञानिक समस्याओं से सम्बन्धित आकंड़ों के संकलन, वर्गीकरण व्याख्या तथा तुलना में ही नहीं बल्कि उनसे सम्बद्ध पूर्वानुमान व भविष्यकथन में भी सांख्यिकी का बहुत उपयोग है।

प्रश्न 4.
सांख्यिकी की सीमाओं की विवेचना कीजिए।
या
“सांख्यिकीय विधियाँ अयोग्य व्यक्तियों के हाथों में खतरनाक औजार हो सकती है।” इस कथन की समीक्षा कीजिए।
उत्तर :
सांख्यिकी की सीमाएँ
(Limitations of Statistics)

सांख्यिकी एक लाभप्रद विज्ञान है। यह जीवन के प्रत्येक क्षेत्र को स्पर्श करता है। सामाजिक विज्ञान शिक्षा तथा मनोविज्ञान में सांख्यिकी का महत्त्वपूर्ण योगदान है। कृषि, नियोजन, अर्थशास्त्र, राजस्व, राजनीतिशास्त्र आदि में भी इसका भरपूर प्रयोग होता है, परन्तु इसका यह अर्थ नहीं है कि सांख्यिकी की कोई सीमाएँ (कमियाँ) ही नहीं हैं। वास्तविकता यह है कि सांख्यिकी जितना लाभदायक विज्ञान है, उतना ही यह ख़तरनाक भी है। इसका प्रयोग बहुत ही सोच-विचारकर, सावधानीपूर्वक तथा विशेषज्ञों द्वारा किया जाना चाहिए। यदि सांख्यिकी का प्रयोग अकुशल व्यक्तियों द्वारा किया जाता है तो यह बहुत हानिप्रद सिद्ध हो सकता है। इसकी सीमाओं पर सावधानीपूर्वक विचार करना चाहिए। सांख्यिकी की प्रमुख सीमाएँ इस प्रकार हैं –

(1) सांख्यिकी केवल संख्यात्मक तथ्यों का अध्ययन करती है, न कि गुणात्मक तथ्यों का – सांख्यिकी की यह महत्त्वपूर्ण कमजोरी है। यह मानव-जीवन के केवल उसी पहलू का अध्ययन करती है जिसे संख्याओं द्वारा प्रस्तुत किया जा सके; जैसे-ऊँचाई, आयु, भार तथा आय आदि। जीवन के गुणात्मक पक्ष; जैसे—सुन्दरता, भावना, दुष्टता, बुद्धिमत्ता, कुटिलता आदि का अध्ययन सांख्यिकी द्वारा नहीं कर सकते हैं। गुणात्मक पहलू को संख्याओं में व्यक्त करके अप्रत्यक्ष रूप में अध्ययन कर सकते हैं। बुद्धिमत्ता का माप अनुमानित संख्याओं द्वारा व्यक्त कर सकते हैं, प्रत्यक्ष रूप में नहीं।

(2) सांख्यिकीय समंक सजातीय और एकरूप होने चाहिए – सांख्यिकी में विजातीय तथ्यों का अध्ययन नहीं किया जा सकता, सांख्यिकीय विधियों द्वारा समंकों की तुलना तभी सम्भव है जबकि वे सजातीय हों तथा उनमें एकरूपता पायी जाये।

(3) सांख्यिकी समूह का अध्ययन करती है, न कि व्यक्ति को प्रो० नीजवैगर के अनुसार, सांख्यिकी के निष्कर्ष समूह के सामूहिक व्यवहार का अनुमान करने में सहायक होते हैं, उस समूह की व्यक्तिगत इकाइयों फ़ा नहीं।” सांख्यिकी व्यक्तिगत इकाई की विशेषता पर ध्यान न देकर सामूहिक विशेषता या औसत पर ध्यान देती है। सांख्यिकी के परिणाम समूह से जुड़े होते हैं, न कि व्यक्ति से। किसी कक्षा के प्राप्तांकों का औसत यह नहीं बताता कि अमुक विद्यार्थी के प्राप्तांक उतने ही होंगे।

(4) बिना सन्दर्भ के सांख्यिकी के परिणाम असत्य और भ्रामक होते हैं – समस्या के बिना सन्दर्भ और पूर्ण जानकारी के सांख्यिकीय परिणाम भ्रामक और असत्य मालूम होते हैं। कुछ समंकों से प्राप्त निष्कर्ष किसी भी विषय पर तब तक लागू नहीं किये जा सकते जब तक कि परिस्थिति, सन्दर्भ व समस्या की पूर्ण जानकारी न हो।

(5) सांख्यिकी के प्रयोग के लिए सांख्यिकीय विधियों की जानकारी आवश्यक – सांख्यिकी विज्ञान की यह एक गम्भीर सीमा है कि इसके सही उपयोग करने के लिए सांख्यिकीय विधियों की पूर्ण व सही जानकारी अति आवश्यक है। जो व्यक्ति सांख्यिकीय विधियों के प्रयोग की पूर्ण जानकारी नहीं रखते हैं, उनके द्वारा इनके प्रयोग से लाभ के स्थान पर नुकसान ही होता है। यूल और केण्डाल ने तो यहाँ तक कहा है, “अयोग्य व्यक्तियों के हाथों में सांख्यिकीय विधियाँ खतरनाक औजार हैं।”

(6) सांख्यिकी के परिणाम दीर्घकाल में तथा औसत रूप में सही होते हैं – प्राकृतिक विज्ञानों; जैसे-रसायनशास्त्र, भौतिकशास्त्र आदि के नियम और परिणाम सार्वभौमिक तथा सार्वकालिक होते हैं। ये अल्पकाल तथा दीर्घकाल सभी कालों में लागू होते हैं, परन्तु सांख्यिकी के परिणाम केवले दीर्घकाल में ही सही निकलते हैं तथा वे एक औसत प्रवृत्ति के परिचायक होते हैं। उनमें छोटे-छोटे उच्चावचन एवं कमियाँ विद्यमान रहती हैं। सांखियकी के नियम सम्भावना सिद्धान्त पर आधारित होते हैं। जिसके अनुसार यदि किसी सिक्के को 20 बार उछालें तो सम्भावना यह है कि 10 बार चित (Head) तथा 10 बार पट (Tail) आएगा; किन्तु ‘यथार्थ में हो सकता है 14 बार चित व 6 बार पट आये।

(7) सांख्यिकी एक साधन है, साध्य नहीं – सांख्यिकी का प्रमुख कार्य समस्या से सम्बन्धित आँकड़े एकत्रित कर उन्हें वर्गीकृत करके सारणीयन तथा रेखाचित्रों द्वारा प्रस्तुत करना है। बाउले के मत में सांख्यिकी का काम परिणाम या निष्कर्ष निकालना नहीं है। यदि सांख्यिकी परिणाम निकालेगी। भी, तो वे निष्पक्ष नहीं होंगे। परन्तु कुछ दूसरे सांख्यिकीवेत्ता यह मानते हैं कि बिना परिणाम के सांख्यिकी अनुपयोगी होगी; अतः निष्कर्ष रूप में यह कह सकते हैं कि समंकों के एकत्रीकरण में पूर्ण सावधानी रखकर तटस्थ रूप में उनका प्रयोग करना चाहिए। अनुसन्धानकर्ता के तटस्थ न रहने पर। परिणाम गलत और हानिकारक हो सकते हैं; अतः सांख्यिकीय विधियों का प्रयोग साधन के रूप में बुद्धिमानीपूर्वक करना चाहिए।

(8) सांख्यिकीय विधि अनुसन्धान की एकमात्र विधि नहीं है – समस्याओं के अनुसन्धान की अनेक विधियाँ हैं, सांख्यिकीय विधि उन अनेक विधियों में से एक हैं। अत: सांख्यिकी से प्राप्त परिणामों को पूर्ण रूप से स्वीकार नहीं किया जाना चाहिए, जब तक कि अनुसन्धान की दूसरी विधियों से परिणामों की पुनः जाँच न कर ली जाए।

अंत में यह कह सकते हैं कि सांख्यिकीय विधियों के प्रयोग में पूर्ण सावधानी रखनी चाहिए। उपर्युक्त सीमाओं को ध्यान में रखकर निष्कर्ष निकालने चाहिए, अन्यथा इसके परिणाम भ्रामक और हानिकारक हो सकते हैं। यही कारण है कि यूल और केण्डाल यह कहने पर मजबूर हुए हैं कि सांख्यिकीय गीतियाँ अयोग्य व्यक्तियों के हाथों में खतरनाक औजार हो सकते हैं।

प्रश्न 5.
सांख्यिकीय श्रेणियों (Statistical series) से आप क्या समझते हैं। इनके विभिन्न प्रकारों का सामान्य विवरण प्रस्तुत कीजिए।
उत्तर :
सांख्यिकीय श्रेणियाँ
(Statistical Series)

संकलिन आँकड़ों को जब एक निश्चित क्रम में लिखा जाता है तो इस भाँति बनी हुई पदमाला या श्रृंखला को सांख्यिकीय श्रेणी (Statistical Series) कहा जाता है। सांख्यिकीय श्रेणी में हम आँकड़ों को एक क्रमबद्ध ढंग से प्रदर्शित करते हैं। कॉनर (Conner) ने सांख्यिकीय श्रेणी की परिभाषा इस प्रकार दी है, “जब दो चल-राशियों के मूल्यों को साथ-साथ इस भाँति व्यवस्थित किया जाए कि एक का मापनीय अन्तरे दूसरे के मापनीय अन्तर का सहगामी हो तो इस प्रकार से प्राप्त पदमाला को सांख्यिकीय श्रेणी कहते हैं।”

सांख्यिकीय श्रेणियों के प्रकार
(Types of Statistical Series)

सांख्यिकीय श्रेणियाँ कई प्रकार की होती हैं। मुख्यतः सांख्यिकीय श्रेणियों की रचना तीन प्रकार से की जा सकती है –

1. व्यक्तिगत श्रेणी
2. असतत या खण्डित या विच्छिन्न श्रेणी
3. सतत् या अखण्डित या अविच्छिन्न श्रेणी।

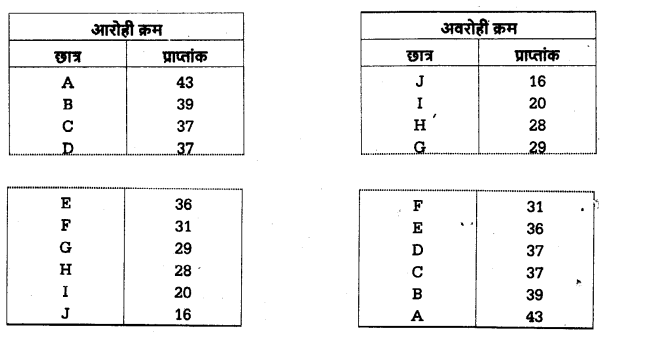
(1) व्यक्तिगत श्रेणी (Individual Series) – व्यक्तिगत श्रेणी वह है जिसमें समूह की प्रत्येक इकाई का मान अलग-अलग दिया जाता है। इस श्रेणी में प्रत्येक पद स्वतन्त्र होता है। व्यक्तिगत श्रेणी का निर्माण उस समय किया जाता है कि जब संकलित आँकड़ों से समूह अथवा वर्ग बनाने सम्भव न हों अथवा हर एक पद को महत्त्व देना हो। इन श्रेणियों की रचना आरोही (Ascending) तथा अवरोही (Descending) दोनों ही क्रमों में की जा सकती है। उदाहरण के लिए निम्नलिखित तालिका में कक्षा XI के दस छात्रों के मनोविज्ञान में प्राप्तांक आरोही तथा अवरोही क्रम में प्रस्तुत किये गये हैं –

(2) असतत या खण्डित या विच्छिन्न श्रेणी (Discrete or Discontinuous Series) – जिस श्रेणी में प्रत्येक मान अलग-अलग नहीं लिखा जाता, अपितु प्रत्येक मान के समक्ष उसकी आवृत्ति लिख दी जाती है, उसे असतत/खण्डित या विच्छिन्न श्रेणी कहा जाता है। यह श्रेणी वास्तविक अन्तर को प्रकट करती है। उदाहरण के लिए—कक्षा XI के 20 छात्रों के मनोविज्ञान में प्राप्तांक निम्नलिखित हैं –

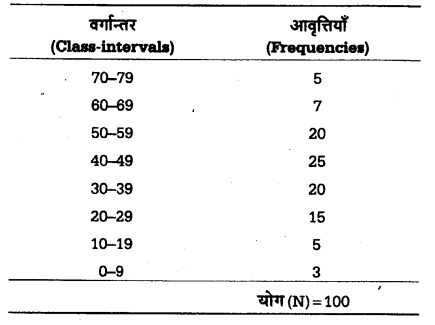
(3) सतत या अखण्डित या अविच्छिन्न श्रेणी (Continuous Series) – सतत श्रेणी में इकाइयों के मानों को वर्गान्तरों (Class-intervals) के रूप में व्यवस्थित किया जाता है। इस प्रकार की श्रेणी में ऐसे मान आते हैं जिनका सूक्ष्म विभाजन सम्भव है; जैसे—समय को घण्टा-मिनट-सेकण्ड आदि में विभाजित किया जा सकता है। बुद्धि, भार, ऊँचाई व लम्बाई आदि को भी सरलता से मापा और उपविभाजित किया जा सकता है। मनोविज्ञान में जिन चल-राशियों का अध्ययन किया जाता है, वे अधिकतर इसी श्रेणी के अन्तर्गत आती हैं। कक्ष X के 100 छात्रों के मनोविज्ञान के प्राप्तांकों का विवरण निम्नलिखित है –

श्रेणियों की रचना में निम्नलिखित बिन्दुओं पर ध्यान देना आवश्यक है –

(i) व्यक्तिगत श्रेणी वस्तुतः असतत या खण्डित श्रेणी का एक विशिष्ट रूप है। यदि असतत श्रेणी में प्रत्येक प्राप्तांक की आवृत्ति 1 हो तो वह व्यक्तिगत श्रेणी का रूप धारण कर लेती है।
(ii) यदि सतत श्रेणी में प्रत्येक वर्गान्तर के मध्य बिन्दु पर उनकी सम्पूर्ण आवृत्तियाँ केन्द्रित मान ली जाये तो यह श्रेणी असतत या खण्डित श्रेणी का रूप धारण कर लेती है।

प्रश्न 6.
ऑकड़ों के व्यवस्थापन से क्या आशय है? आँकड़ों के व्यवस्थापन के मुख्य प्रकारों का विस्तृत विवरण प्रस्तुत कीजिए।
उत्तर :
आँकड़ों का व्यवस्थापन या आवृत्ति विवरण
(Organization of the Data or Frequency Distribution)

मनोविज्ञान के क्षेत्र में विभिन्न समस्याओं को लेकर अध्ययन, प्रयोग एवं अनुसन्धान कार्य किये जाते हैं। ये प्रयोग या अनुसन्धान कार्य एक विशाल समूह पर किये जाते हैं। जिनके फलस्वरूप हमें आँकड़े प्राप्त होते हैं। ये आँकड़े हमारे लिए तब तक निरर्थक हैं जब तक कि उन्हें व्यवस्थित रूप प्रदान नहीं कर दिया जाता। इस भाँति, आँकड़ों को सार्थक एवं उपयोगी बनाने के लिए व्यवस्थापन या आवृत्ति वितरण का विशेष महत्त्व है।

संगृहीत आँकड़ों से सुगमतापूर्वक निष्कर्ष निकालने हेतु इनका व्यवस्थापन (Organization) किया जाता है। जिसमें आँकड़ों का वर्गीकरण तथा सारणीयन सम्मिलित है। संगृहीत आँकड़ों को सर्गों तथा सारणियों के रूप में निरूपित करना ही आँकड़ों का व्यवस्थापन या आवृत्ति वितरण है। मुख्यत: व्यवस्थापन की तीन पद्धतियाँ हैं –

1. वर्गीकरण (Classification)
2. सारणीयन (Tabulation) तथा
3. रेखाचित्र प्रस्तुतीकरण (Graphical Representation)।

आँकड़ों का वर्गीकरण समानता या सजातीयता के आधार पर किया जाता है; जैसे–सामाजिक स्तर या धर्म के आधार पर वर्गीकरण। आँकड़ों का वर्गीकरण करने के बाद उनके आपसी सम्बन्ध तथा प्रकृति का ज्ञान प्राप्त करने के लिए उनका सारणीयन किया जाता है जिसे अधिक स्पष्ट रूप से समझने के लिए रेखाचित्रों के माध्यम से आँकड़ों का प्रस्तुतीकरण किया जाता है।

मूल आँकड़ों के व्यवस्थापन के प्रकार
(Types of Basic Datas Distribution)

मनोवैज्ञानिक अध्ययनों या अनुसन्धान कार्यों में मूल आँकड़े अधिक संख्या में तथा विस्तृत (फैले हुए) होते हैं जिन्हें व्यवस्थापन की प्रक्रिया द्वारा सुस्पष्ट एवं सार्थक बनाया जाता है। आँकड़ों के व्यवस्थापन के प्रमुख तीन प्रकार हैं –

1. साधारण व्यवस्था
2. आवृत्ति व्यवस्था तथा
3. आवृत्ति वितरण।

(1) साधारण व्यवस्था (Simple Array) – साधारण व्यवस्था आँकड़ों को व्यवस्थित करने की सबसे सरल विधि है जिसमें आँकड़ों को आरोही या अवरोही क्रम में व्यवस्थित किया जाता है। आँकड़ों को इस प्रकार विन्यसित करने से उनकी प्रकृति स्पष्ट हो जाती है। आँकड़ों को साधारण व्यवस्था में उस समय व्यवस्थित किया जाना चाहिए जबकि आँकड़ों की संख्या कम हो। इस व्यवस्था की सबसे बड़ी परिसीमा यह है कि इससे अन्य सांख्यिकी गणनाओं में सहायता नहीं मिलती है।

उदाहरण 1 – कक्षा XI के 10 छात्रों के मनोविज्ञान में प्राप्तांक (पूर्णाक 50) निम्न प्रकार हैं –

अब इन्हें साधारण व्यवस्था के अन्तर्गत आरोही व अवरोही क्रम में इस प्रकार प्रदर्शित किया जाएगा –

(2) आवृत्ति व्यवस्था (Frequency Array) – आँकड़ों की प्रकृति अधिक स्पष्ट करने के लिए उनका व्यवस्थापन आवृत्तियों के आधार पर किया जाता है। साधारण व्यवस्था से आवृत्ति व्यवस्था अधिक अच्छी समझी जाती है, किन्तु इसे तभी प्रयोग किया जाना चाहिए जबकि आँकड़ों की संख्या कम हो तथा उनकी आवृत्ति बार-बार हुई हो।

उदाहरण 2 – नीचे की तालिका में एक कक्षा के 100 विद्यार्थियों को बुद्धि-लब्धि के आधार पर विभाजित किया गया है –

(3) आवृत्ति वितरण (Frequency Distribution) – आवृत्ति वितरण एक ऐसी व्यवस्था है। जिसमें पदों (चरों) के मूल्य तथा उनकी आवृत्तियाँ दी हुई होती हैं। आवृत्ति वितरण के दो प्रमुख तत्त्व हैं –
(i) पद (चर) तथा (ii) आवृत्तियाँ।

(i) पद (Variable) – पद या चर वह संख्यात्मक तथ्य है जो मात्रा या आकार में परिवर्तित होता रहता है; जैसे—आयु, लम्बाई, भार, आय या प्राप्तांक आदि। पद या चर दो प्रकार के हैं(अ) सतत चर तथा (ब) असतत या खण्डित चर। पद या चर को ‘x’ से प्रदर्शित करते हैं।

(ii) आवृत्तियाँ (Frequencies) – किसी प्राप्तांक के बार-बार आने की प्रवृत्ति को आवृत्ति (Frequency) कहते हैं। इकाइयों (व्यक्तियों) की वह संख्या जो किसी वर्ग-विशेष में आती है, उस वर्ग की आवृत्ति या बारम्बारता कहलाती है। इस प्रकार आवृत्तियाँ वह संख्या है जो किसी वर्ग-विशेष के पदों (मूल्यों) को ग्रहण करती है। कोई प्राप्तांक/पद या संख्या यदि पाँच बार आती है तो उस प्राप्तांक की आवृत्ति ‘5’ होगी। आवृत्ति को ‘f’ से प्रकट करते हैं। प्रत्येक वर्ग के अन्तर्गत आने वाले पदों की संख्या उस वर्ग की आवृत्ति कहलाती है।

इन आवृत्तियों को सुविधानुसार भिन्न-भिन्न वर्गों में वितरित अथवा प्रदर्शित करने की विधि आवृत्ति वितरण कहलाती है।

सरल आवृत्ति वितरण
(Simple Frequency Distribution)

सरल आवृत्ति वितरण में सर्वाधिक तथा सबसे कम प्राप्तांकों तथा उनके मध्य जितने भी प्राप्तांक आ सकते हैं उन सभी को आकार के अनुसार लिखा जाता है। फिर हर एक प्राप्तांक के सामने वह अंक लिखा जाता है जितनी बार वह प्राप्तांक दोहराया गया है। यही उस पद की आवृत्ति है।

ये सभी प्राप्तांक अव्यवस्थित, अपरिष्कृत तथा अवर्गीकृत हैं जिन्हें न तो मस्तिष्क में अंकित रखा जा सकता है और न ही इन्हें देखकर मनोविज्ञान की कक्षा के बारे में कोई सुनिश्चित धारणा ही बनायी जा सकती है। हम इन्हें पहले सरल आवृत्ति वितरण के रूप में प्रदर्शित करते हैं –

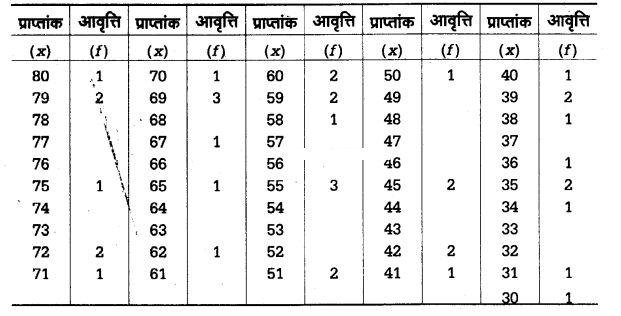
सरल आवृत्ति वितरण से प्रत्येक प्राप्तांक की आवृत्ति ज्ञात हो जाती है। प्राप्तांकों का वितरण अर्थात् अधिकांश विद्यार्थियों ने कम अंक प्राप्त किये हैं या उच्च अंक तथा सामान्य अंक पाने वाले विद्यार्थी कितने हैं, इन सभी बातों का हमें आसानी से ज्ञात हो जाता हैं। किन्तु सरल आवृत्ति वितरण बहुत अधिक स्थान घेरता है; अतः हम आवृत्ति वितरण बनाने की वह प्रक्रिया अपनाएँगे जो कुछ क्रुमबद्ध सोपानों पर आधारित होती है। आवृत्ति वितरण तालिका की यह प्रक्रिया निम्नलिखित है –

आवृत्ति वितरण तालिका निर्माण की प्रक्रिया
(Procedure of Preparing a Frequency Distribution Table)

आवृत्ति वितरण तालिका निर्माण की प्रक्रिया के पाँच प्रमुख सोपान हैं जिनके आधार पर आवृत्ति वितरण तालिका आसानी से निर्मित हो सकती है। ये सोपान निम्न प्रकार वर्णित हैं—

(1) प्रसार क्षेत्र (Range) – आवृत्ति वितरण तालिका बनाने के लिए सबसे पहले प्रसार क्षेत्र ज्ञात कर लेना चाहिए। आँकड़ों में उच्चतम अंक (Highest Score) तथा न्यूनतम अंक (Lowest Score) के अन्तर को प्रसार क्षेत्र कहते हैं।

प्रसार क्षेत्र = उच्चतम अंक – न्यूनतम अंक
Range = Highest Score – Lowest Score or Range =H.S. – L.S.

(2) वर्गान्तर (Class-anterval : C.I.) – प्रसार क्षेत्र ज्ञात करने के उपरान्त वर्गान्तर की संख्या ज्ञात की जाती है जो साधारणत: 5 से लेकर 20 तक हो सकती है। कुछ विद्वानों की राय में यह 10 से कम तथा 20 से अधिक नहीं होनी चाहिए। परिणामों की शुद्धता का ध्यान रखते हुए वर्गान्तरों की संख्या 10 से 15 तक रखना उपयुक्त है।

वर्गान्तरों की संख्या ज्ञात करने के लिए आवश्यक है कि वर्गान्तर का आकार (Size of C.I.) पता लगाया जाये। वर्गान्तर का आकार सुनिश्चित करने के लिए निम्नलिखित सूत्र प्रयुक्त होता है –

गणना सम्बन्धी कार्य (जोड़ना व घटाना ओदि) में सुविधा की दृष्टि से वर्गान्तर का आकार ऐसा चुना जाये जो 5 से पूरी तरह विभाजित हो जाये। प्रश्न हल करते समय प्रसार क्षेत्र को सिर्फ 5 से भाग देकर वर्गान्तर का आकार ज्ञात कर लेना चाहिए। यदि प्रश्न में वर्गान्तर का आकार दिया हुआ हो तो फिर आकार ज्ञात करने की कोई आवश्यकता नहीं होती।

(3) वर्गान्तरों का निर्माण (Construction of Class-intervals) – वर्गान्तरों की संख्या तथा उनका आकार ज्ञात करने के बाद वर्गान्तरों का निर्माण किया जाता है। प्रथम वर्गान्तर बनाते समय निम्नतम अंक सर्वप्रथम लिखा जाता है, फिर निम्नतम अंक में वर्गान्तर के आकार को जोड़कर उसके सामने लिख देते हैं। उदाहरण (3) में निम्नतम अंक 30 है तथा वर्गान्तर का आकार 5 है। अत: पहले 30 लिखा जाएगा, फ़िर 30 में 5 जोड़कर (30 + 5) यानि 35 लिखा जायेगा। इस तरह से पहला वर्गान्तर 30-35 बना।

इसके आगे, पहले वर्गान्तर 30-35 की ऊपरी सीमा दूसरे वर्गान्तर की निम्न सीमा बन जायेगी तथा 35 में 5 जोड़कर (35+ 5) यानी 40, यह दूसरे वर्गान्तर की ऊपरी सीमा होगी। इस भाँति, दूसरा वर्गान्तर होगा 30-40। तीसरे वर्गान्तर की निम्न सीमा 40 होगी जिसमें वर्गान्तर का आकार 5 जोड़ने पर 40 + 5 = 45, इसकी ऊपरी सीमा बनेगी और तीसरा वर्गान्तर 40-50 होगा। वर्गान्तर बनाने का यह क्रम तब तक चलता जायेगा जब तक कि उच्चतम अंक वर्गान्तर में शामिल न हो जाये।

नोट – वर्गान्तरों का निर्माण करते समय निम्नलिखित बातों का ध्यान रखना चाहिए

(i) अक्सर प्राप्तांकों के न्यूनतम अंक से ही वर्गान्तर बनाना शुरू करते हैं; जैसे—उपर्युक्त उदाहरण में न्यूनतम अंक 30 से वर्गान्तर बनाना प्रारम्भ किया गया है।

(ii) गणना को सुविधाजनक बनाने की दृष्टि से ‘वर्गान्तरों को न्यूनतम अंक से भी छोटा या कम अंक से शुरू किया जा सकता है। उदाहरणार्थ-यदि न्यूनतम अंक 26 है और वर्गान्तर का आकार 5 है तो 26-31 वर्गान्तर बन जाता है और यह 25-30 वर्गान्तर भी बन सकता है। वैसे वर्गान्तर 25-30 गणना की दृष्टि से सरल व सुविधाजनक कहा जाएगा।

(iii) यदि निम्नतम प्राप्तांक 5 से कम है तथा आकार 5 या 5 से ज्यादा है तो प्रथम वर्गान्तर ‘शून्य’ से प्रारम्भ करना चाहिए। यदि प्रथम वर्गान्तर ‘शून्य से प्रारम्भ है और वर्गान्तर का आकार 5 है। तो प्रथम वर्गान्तर 0-4 होगा। यहाँ यह स्पष्ट करना उचित है कि 0-4 वर्गान्तर में 5 प्राप्तांक हैं। यानि 0, 1, 2, 3 व 4। इसलिए इस समूह में 0 से लेकर 4 तक अंक पाने वाले सभी व्यक्ति शामिल हो जाएँगे। इस क्रम में दूसरा वर्गान्तर 5 से शुरू होगा तथा 9 पर समाप्त हो जाएगा यानि यही वर्गान्तर 5-9 होगा इसमें भी 5 प्राप्तांक शामिल हैं – 5, 6, 7, 8 व 9।

(iv) वर्गान्तरों को आरोही क्रम (Ascending Order) तथा अवरोही क्रम (Descending Order) दोनों में से किसी भी क्रम में लिखा जा सकता है।

आवृत्ति तालिका का निर्माण करते समय अव्यवस्थित आँकड़ों के पहले प्राप्तांक को पढ़कर अनुमान लगायें कि यह किस वर्गान्तर में आता है। जिस वर्गान्तर में यह अंक आता हो, उसके सामने एक अंकदण्ड लगा देना चाहिए। अब दूसरा प्राप्तांक पढ़कर सम्बन्धित वर्गान्तर में उसके सामने एक अंकदण्ड लगा दें। इसी तरह से एक के बाद एक सभी प्राप्तांकों को पढ़कर अंकदण्ड लगा दिये जाते हैं। जैसे—उदाहरण (3) में पहला प्राप्तांक 42 है जिसके लिए 40-45 वर्गान्तर के सामने एक अंकदण्ड लगा देंगे। अभिप्राय यह है कि यही क्रिया सभी प्राप्तांकों के लिए दोहराई जाएगी।

(5) अंकदण्डों का आवृत्तियों में बदलना (Changing Tallies in Frequencies)- वर्गान्तरों के सम्मुख आवृत्तियों के अंकदण्डों द्वारा प्रदर्शन के बाद अंकदण्डों को आवृत्तियों में बदलकर लिख दिया जाता है। इसके लिए अंकदण्डों को जोड़कर योग को आवृत्ति (Frequencies) वाले खाने में लिख देते हैं। उदाहरण (3) के 55-60 वर्गान्तर में  छह अंकदण्ड हैं; अत: इस वर्गान्तर के सामने आवृत्ति वाले खाने में 6 लिखा गया है। इसी प्रकार से सभी वर्गान्तरों के सामने के अंकदण्डों को आवृत्तियों में बदल दिया जाता है। यदि आवृत्ति वितरण तालिका में अंकदण्डों को लगाने में कोई त्रुटि नहीं है तो आवृत्तियों (f) का योगफल व्यक्तियों की कुल संख्या (N) के बराबर होता है।

अब हम उदाहरण (3) के अन्तर्गत सरल आवृत्ति वितरण के आधार पर आरोही तथा अवरोही क्रम में आवृत्ति वितरण तालिकाओं को निर्माण करेंगे।

आवृत्ति वितरण तालिका
(Frequency Distribution Table)

उदाहरण 4 – कक्षा XI के 50 परीक्षार्थियों ने मनोविज्ञान में नीचे दिये गए अंक प्राप्त किये। इन प्राप्तांकों का आवृत्ति वितरण तैयार कीजिए –

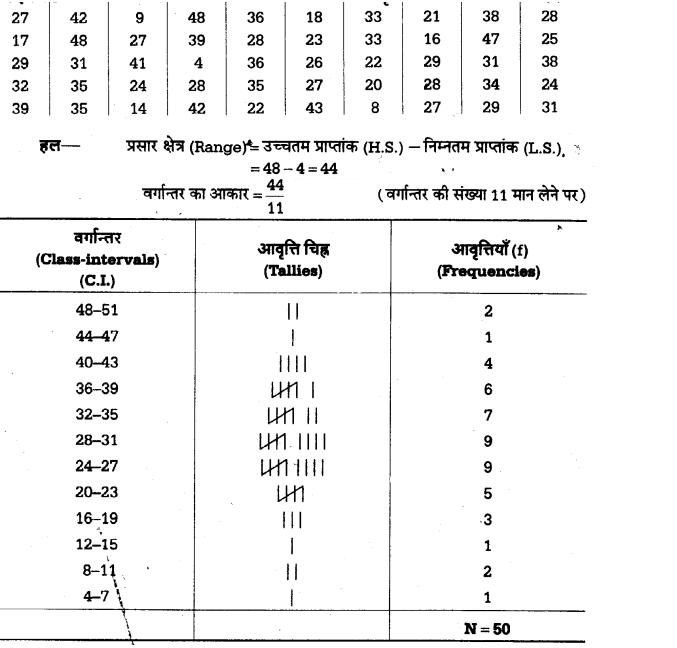
उदाहरण 5 – निम्नलिखित प्राप्तांकों से उचित वर्गान्तरलेकर आवृत्ति-वितरण तालिका बनाइए –

उदाहरण 6 – कक्षा x के 50 छात्रों के भार (पौण्ड्स में) ज्ञात किये गये। इन भारों से उचित वर्गान्तर द्वारा आवृत्ति वितरण तालिका तैयार कीजिए –

संचयी आवृत्तियाँ ज्ञात करना।
(To Find out the Cumulative Frequencies)

किसी आवृत्ति वितरण तालिका में संचयी आवृत्तियाँ (Cumulative Frequencies : C.E:) ज्ञात करने के लिए प्रत्येक वर्ग के सम्मुख उस वर्ग की आवृत्तियों तथा उस वर्ग के नीचे वाले कुल वर्गों की आवृत्तियों का योग लिख दिया जाता है।

उदाहरण 7 – एक स्कूल के 32 शिक्षकों की आयु (वर्षों में दर्शाने वाली संचयी आवृत्तियाँ निम्न प्रकार सारणीबद्ध हैं –

उपर्युक्त उदाहरण में 20-25 वाले वर्गान्तर की संचयी आवृत्ति 4 + 0 = 4 है; क्योंकि इस वर्गान्तर से नीचे आवृत्तियों की संख्या ‘शून्य’ (अर्थात् कुछ भी नहीं) है। इसी भाँति

25 – 30 वाले वर्गान्तर की संचयी आवृत्तियाँ = 4 + 8 = 12
30 – 35 वाले वर्गान्तर की संचयी आवृत्तियाँ = 7 + 12 = 19
35 – 40 वाले वर्गान्तर की संचयी आवृत्तियाँ = 4 + 19 = 23
40 – 45 वाले वर्गान्तर की संचयी आवृत्तियाँ = 4 + 23 = 27
45 – 50 वाले वर्गान्तर की संचयी आवृत्तियाँ = 2 + 27 = 29
50 – 55 वाले वर्गान्तर की संचयी आवृत्तियाँ = 2 + 29 = 31
55 – 60 वाले वर्गान्तर की संचयी आवृत्तियाँ = 1 + 31 = 32

प्राप्तांकों को समूहबद्ध करने की विधियाँ
(Methods of Grouping Scores)

प्राप्तांकों को समूहबद्ध करने की तीन विधियाँ हैं –

1. समावेशी विधि (Inclusive Method)
2. शुद्ध वर्गीकृत श्रृंखला (Pure Classification Series)
3. अपवर्जी विधि (Exclusive Method)

(1) समावेशी विधि (Inclusive Method) – समावेशी विधि में वर्गान्तर का अन्तिम अंक वर्गान्तर में ही शामिल है। उदाहरणार्थ-40-44 का अर्थ है कि 40 से लेकर 44 तक के प्राप्तांक इसी वर्ग में सम्मिलित हैं। इसी प्रकार 45-49 का अर्थ है कि 45 से लेकर 49 तक के सभी प्राप्तांक इस वर्ग में सम्मिलित हैं। समावेशी विधि द्वारा आवृत्ति वितरण सरलता से एवं बिना किसी त्रुटि के बनाये जा सकते हैं; अत: यह विधि प्राप्तांकों को समूहबद्ध करने की सर्वश्रेष्ठ विधि है।

(2) शुद्ध वर्गीकृत श्रृंखला (Pure Classification Method) – यह विधि सांख्यिकीय दृष्टि से विशुद्ध हैं; क्योंकि इसमें वास्तविक सीमाएँ प्रदर्शित की गयी हैं। यहाँ प्रत्येक वर्ग की उच्चतम तथा निम्नतम सीमाएँ जानने के लिए प्राप्तांकों की वास्तविक सीमाओं की गणना करते हैं। निम्नतम सीमा जानने के लिए उसे प्राप्तांक में से 0.5 घटा देते हैं तथा उचचतम सीमा जानने के लिए 0.5 जोड़ देते हैं। उदाहरण के लिए-पहले वर्गान्तर 40-44 की निम्नतम सीमा 40-0.5 = 39.5 हुई और उच्चतम सीमा 44+ 0.5 = 44.5 हुई। इसी तरह से सभी वर्गों का निर्माण करते हैं। इस विधि की परिसीमा यह है कि इसमें समय अधिक व्यय होता है।

(3) अपवर्जी विधि (Exclusive Method) – अपवर्जी विधि में वर्गान्तर 40-45 का अर्थ यह है कि इस वर्ग में 40 से लेकर 44 तक के अंक शामिल हैं किन्तु 45 शामिल नहीं हैं। 45 प्राप्तांक पहले वर्ग में न होकर दूसरे वर्ग में है। इसी प्रकार वर्गान्तर 45-50 का अर्थ है कि इसमें 45 से 49 तक शामिल हैं लेकिन 50 नहीं। 50 तीसरे वर्ग में है। अपवर्जी विधि का एक दोष यह है कि इसमें कभी-कभी भ्रमवश आवृत्ति चिह्न (अंकदण्ड) गलत वर्ग के सामने लग जाता है। क्योंकि 50 का अंक 45-50 में भी लिखा है और 50-55 में भी, जबकि इसे शामिल 50-55 वाले वर्ग में करना है; अतः यह ध्यान रखना चाहिए।

वर्गान्तर का मध्य-बिन्द ज्ञात करना
(Mid-point of a Class Interval)

किसी वर्गान्तर का मध्य-बिन्दु (Mid-point) उस वर्गान्तर के निम्नतम और उच्चतम प्राप्तांकों को जोड़कर तथा योग का आधार करने पर प्राप्त हो सकता है। इसके लिए अग्रलिखित सूत्र प्रयोग करते हैं –

प्रश्न 7.
केन्द्रीय प्रवृत्ति की माप से क्या आशय है। केन्द्रीय प्रवृत्ति की माप के मुख्य उद्देश्य का भी उल्लेख कीजिए।
या
केन्द्रीय प्रवृत्ति की माप से आप क्या समझते हैं?
उत्तर :
समंकों की महत्त्वपूर्ण विशेषताओं को स्पष्ट करने के लिए सांख्यिकीय विश्लेषण में केन्द्रीय प्रवृत्ति (Central Tendency) की माप का महत्त्वपूर्ण स्थान है। समंकों के वर्गीकरण तथा सारणीयन से समंक सरल, सुबोध, व्यवस्थित तथा तुलनीय तो बन जाते हैं किन्तु इससे उनकी महत्त्वपूर्ण विशेषताएँ प्रकट नहीं होतीं; अत: एक ऐसी विधि की आवश्यकता है जिसके द्वारा एक ही संख्या से सभी संगृहीत आँकड़ों को प्रतिनिधित्व कराया जा सके। इसके लिए केन्द्रीय प्रवृत्ति की मापों या सांख्यिकीय माध्यमों का अध्ययन आवश्यक है।

केन्द्रीय प्रवृत्ति की माप : अर्थ
(Definitions of Measures of Central Tendency or Average)

संगृहीत आँकड़ों के मध्य ऐसी संख्या, जो सभी आँकड़ों का प्रतिनिधित्व करती हो, तो न तो समूह की न्यूनतम मान वाली संख्या होगी और न ही अधिकतम मान वाली। अवश्य ही, वह संख्या समूह के मध्य या उसके आस-पास की संख्या होगी। अत; आँकड़ों में से किस एक आँकड़े के पास पाये जाने की उनकी प्रवृत्ति को केन्द्रीय प्रवृत्ति (Central Tendency) कहा जाता है तथा इस माध्य या औसत को केन्द्रीय माप या केन्द्रीय प्रवृत्ति की मान कहते हैं।

इस भाँति केन्द्रीय प्रवृत्ति से तात्पर्य उस मान से है जो प्राप्त आँकड़ों का प्रतिनिधित्व करता है। अर्थात् वह मान जो प्राप्त आँकड़ों में सबसे अधिक बार आया हो। साधारणत: केन्द्रीय प्रवृत्ति की मापों से हमारा अर्थ ‘सांख्यिकीय माध्य’ या ‘औसत (Average) से होता है; क्योंकि सांख्यिकी माध्यम के आस-पास सभी आँकड़े वितरित होते हैं।

वह संख्या, जो किसी समूह-विशेष के सभी आँकड़ों का प्रतिनिधित्व करती है, उस समूह का सांख्यिकीय माध्य से औसत कहलाती है।

केन्द्रीय प्रवृत्ति की माप या सांख्यिकीय माध्य की परिभाषाएँ
(Definitions of Measures of Central Tendency or Average)

सांख्यिकीय माध्य या केन्द्रीय प्रवृत्ति की माप की प्रमुख परिभाषाएँ निम्नलिखित हैं –

(1) सिम्पसन और काक्का के अनुसार, “केन्द्रीय प्रवृत्ति का माप एक ऐसा प्रतिरूपी मूल्य है। जिसकी ओर अन्य संख्याएँ केन्द्रित होती हैं।”

(2) क्लार्क और शकाडे के मत में, “माध्ये सम्पूर्ण समंक समूह का विवरण देने वाली एकमात्र संख्या प्राप्त करने का प्रयत्न है।”

(3) क्रॉक्सटन और काउडेन के मतानुसार, “माध्य समंकों के विस्तार के अन्तर्गत स्थित एक ऐसा पद है। जिसका प्रयोग श्रेणी के सभी पदों का प्रतिनिधित्व करने के लिए किया जाता है। समंक माला के विस्तार के अन्तर्गत स्थित होने के कारण माध्य को कभी-कभी केन्द्रीय मूल्य का माप भी कहा जाता है।

समंक माला के कुछ पद (मूल्य) माध्य से छोटे तथा कुछ मूल्य बड़े होते हैं; अत: माध्य समंक श्रेणी की केन्द्रीय प्रवृत्ति को प्रदर्शित करता है। अन्त में कह सकते हैं कि माध्य समंक श्रेणी का मध्य मूल्य होता है जो श्रेणी की बनावट वे महत्त्वपूर्ण विशेषताओं को बतलाता है।

केन्द्रीय प्रवृत्ति की माप या सांख्यिकीय माध्य के उद्देश्य
(Objectives of Averages)

केन्द्रीय प्रवृत्ति की माप या औसत या सांख्यिकीय माध्य के महत्त्वपूर्ण उद्देश्य निम्नलिखित है।

(1) जटिल तथ्यों को सरल रूप में प्रस्तुत करना – जिससे वे आसानी से समझ में आ सकें।

(2) विस्तृत तथ्यों को संक्षिप्तता प्रदान करना – माध्य तथ्यों के विशाल समूह को एक संख्या के रूप में प्रस्तुत कर देता है। इससे विशाल समूह की जानकारी प्राप्त हो जाती हैं। मोरेनो के अनुसार, माध्य का उद्देश्य व्यक्तिगत मूल्यों के समूह का सरल और संक्षिप्त रूप में प्रतिनिधित्व करना है। जिससे मस्तिष्क समूह की इकाइयों के सामान्य आकार को असानी से समझ सके।”

(3) समग्र की रचना तथा विशेषताओं की जानकारी प्रदान करना – माध्य के द्वारा सारे समूह की सामान्य बनावट (रचना) की जानकारी मिल जाती है। सम्पूर्ण समूह की महत्त्वपूर्ण विशेषताओं तथा गुणों की जानकारी भी मिलती है।

(4) तुलना में सहायता – माध्यों के द्वारा दो या दो से अधिक समूहों, प्रदेशों के कुछ खास लक्षणों का तुलनात्मक अध्ययन कर सकते हैं। दो कक्षा के छात्रों के माध्य से उनके भार या ऊँचाई की जानकारी मिल जाती है।

(5) मार्गदर्शक के रूप में कार्य करना – सांख्यिकीय माध्यम मार्गदर्शक के रूप में कार्य करता है। माध्य की जानकारी से समूह के विकास सम्बन्धी नीतियों के निर्धारण में सहायता मिलती है।

(6) सांख्यिकीय विश्लेषण का आधार – माध्यम विभिन्न वर्गों में गणितीय सम्बन्ध स्थापित करता है। माध्य से विभिन्न समूहों का सांख्यिकीय विश्लेषण किया जाता है।

(7) माध्य बहुत बड़े समूह या वार्ड के प्रतिनिधि के रूप में कार्य किया करता है।

अन्त में कह सकते हैं कि माध्यों का विश्लेषण में महत्त्वपूर्ण स्थान है। डॉ० बाउले के शब्दों में, “माध्य का उद्देश्य जटिल समूहों तथा विशाल क्रियाओं को कुछ महत्त्वपूर्ण शब्दों में या संख्याओं में प्रस्तुत करना है।”

प्रश्न 8.
मध्यमान अथवा समान्तर माध्य (Mean) से आप क्या समझते हैं? मध्यमान ज्ञात करने की विधियों का विस्तृत विवरण प्रस्तुत कीजिए।
या
मध्यमान की परिभाषित कीजिए।
उत्तर :
मध्यमान अथवा समान्तर माध्य
(Mean or Arithmetic Mean)

अंकगणित में जिस मान को औसत (Average) कहा जाता है, उसे हम सांख्यिकी में मध्यमान अथवा समान्तर माध्य (Mean or Arithmetic Mean) कहते हैं। मध्यमान को ‘M’ अक्षर द्वारा प्रदर्शित करते हैं।

परिभाषा – “मध्यमान वह मान है जो दिये हुए पदों के योगफल में पदों की संख्या से भाग देने पर प्राप्त होता है।”

या किसी अंक-सामग्री के समस्त अंकों के योगफल को उन अंकों की संख्या से भाग देने से जो भागफल प्राप्त होता है, उसे मध्ययान कहते हैं।”

या “मध्यमान वह प्राप्तांक है जिसके दोनों ओर विचलन समान होता है।”

उदाहरण 1 – यदि कक्षा 8 के पाँच विद्यार्थियों के भार क्रमानुसार 54, 2, 56, 53 तथा 50 किलोग्राम हों तो इनके मध्यमान की गणना कीजिए।

मध्यमान ज्ञात करना
(Calculation of Mean)

मध्यमान अव्यवस्थित (Ungrouped) तथा व्यवस्थित (Grouped) दोनों ही प्रकार के प्राप्तांकों की मदद से निकाला जा सकता है –

(I) अव्यवस्थित प्राप्तांकों से मध्यमान की गणना (The mean of the Ungreuped Scores) – (N) अव्यवस्थित प्राप्तांकों को मध्यमान निकालने के लिए अव्यवस्थित अंकों को जोड़ लेते हैं तथा प्राप्त योगफल को अंकों की संख्या से भाग दे देते हैं। इसके लिए निम्नलिखित सूत्र का प्रयोग किया जाता है –

उदाहरण 3 – नीचे तालिका में प्राप्तांक तथा उनके सामने आवृत्तियाँ लिखी गयी हैं, मध्यमान की गणना कीजिए –

1. सबसे पहले प्रत्येक वर्गान्तर (Class-interval) का मध्य-बिन्दु ज्ञात किया जाता है।
2. प्रत्येक मध्य-बिन्दु को तत्सम्बन्धी आवृति से गुणा कर लेते हैं।
3. गुणनफलों के योगफल को आवृत्तियों की कुल संख्या से विभाजित कर देते हैं।

उदाहरण 4 – मीचे दी गयी सारणी का दीर्घ विधि द्वारा मध्यमान ज्ञात कीजिए –

उदाहरण 5 – निम्नांकित सारणी का दीर्घ विधि द्वारा मध्यमान ज्ञात कीजिए –

(2) संक्षिप्त विधि (Short Method) – मध्यमान की गणना की दीर्घ विधि में समय बहुत ज्यादा लगता है; अत: सामान्यतया, संक्षिप्त विधि से मध्यमान की गणना की जाती है। इसके क्रमागत पद निम्नलिखित हैं –

1. 1. सबसे पहले वर्गान्तरों के बीच से मध्यवर्ती वर्गान्तर ज्ञात किया जाता है। इस मध्यवर्ती वर्गान्तर का मध्य-बिन्दु ही कल्पित मध्यमान (Assumed Mean) है। सर्वाधिक आवृत्तियों वाले, वर्गान्तर को मध्यवर्ती वर्गान्तर मानना उचित होता है।
   2. इस कल्पित मध्यमान को प्रत्येक मध्य-बिन्दु में से घटाकर विचलन (Deviation) (X- A) ज्ञात किया जाता है।
   3. अब विचलन को वर्ग–अन्तराल से भाग देते हैं। भागफल को संक्षिप्त विचलन Step Deviation) (d) कहते हैं।
   4. स्पष्टंत: कल्पित मध्यमान वाले वर्गान्तर के सामने वाले स्तम्भ में ‘0’ लिखा जाएगा। वितरण के जिस ओर मध्य-बिन्दुओं का मान बढ़ता है, उस तरफ विचलन क्रमशः धनात्मक +1,+2, +3, +4,… आदि होता है तथा जिस ओर मध्य-बिन्दुओं का मान घटता है, उस तरफ विचलन क्रमागत ऋणात्मक -1-2-3,-4… आदि होता है।
   5. अब (fd) ज्ञात किया जाता है जिसके लिए वर्गान्तर के सामने की आवृत्तियों को विचलन से गुणा कर देते हैं और (fd) वाले खाने में लिखते हैं।
   6. (∑fd) की गणना के लिए धनात्मक व ऋणात्मक संख्याओं का अलग-अलग योग ज्ञात करके दोनों का अन्तर ज्ञात कर लिया जाता है।
   7. वर्गान्तर का आकार तथा N का मान प्रश्न से देखकर लिख लिया जाता है और सूत्र में ज्ञात मानों को रखकर मध्यमान की गणना कर ली जाती है।

उदाहरण 7 – नीचे दी गयी सारणी का संक्षिप्त विधि से मध्यमान ज्ञात कीजिए –

प्रश्न 9.
मध्यांक या माध्यिका (Median) से आप क्या समझते हैं? मुख्य विशेषताओं का उल्लेख करते हुए इसकी गणना की विधि का वर्णन कीजिए।
उत्तर :
मध्यांक अथवा माध्यिका
(Median)

मध्यांक (या माध्यिका) (Median) दिये हुए आँकड़ों को दो समूहों में विभक्त कर देता है जिसके एक समूह के प्रत्येक पद का मान मध्यांक से कम और दूसरे समूह का मान मध्यांक से अधिक होता है।

परिभाषा – (1) “यदि आँकड़ों को आरोही या अवरोही क्रम में व्यवस्थित किया जाये तो बिल्कुल मध्य में पड़ने वाला आँकड़ा ‘मध्यांक’ कहलाता है।”

(2) गैरेट के अनुसार, “जब अव्यवस्थित अंक (Ungrouped Scores) या दूसरी माप, क्रम में व्यवस्थित हो तो मध्य का अंक मध्यांक कहलाता है।”

मध्यांक का संकेत चिह्न Md है।

उदाहरण 1 – किसी कक्षा के पाँच बच्चों की ऊँचाई क्रमानुसार 140, 143, 145, 147, 152 सेमी हैं। और इन्हें ऊँचाईं के आरोही क्रम में खड़ा किया गया है। इनका मध्यांक क्या होगा?

हल – ऊँचाइयाँ आरोही क्रम में-140, 143, 145, 147, 152 पाँच बच्चों की ऊँचाइयों का मध्यांक तीसरे बच्चे की ऊँचाई =145 सेमी होगा।

मध्यांक की विशेषताएँ
(Characterisitics of Median)

मध्यांक की मुख्य विशेषताएँ निम्नलिखित हैं –

1. मध्यांक श्रेणी का केन्द्रीय मूल्य होता है; अत: मध्यांक निर्धारण के लिए श्रेणी को किसी क्रम में व्यवस्थित करना आवश्यक है।
2. यह श्रेणी का मध्य अंक (बिन्दु) है जिसके ऊपर व नीचे की ओर आधे-आधे प्राप्तांक स्थित होते हैं; अत: मध्यांक का मान इस बात पर निर्भर है कि उसके ऊपर-नीचे कितने प्राप्तांक स्थित हैं, न कि इस बात पर कि उससे प्राप्तांक कितनी दूरी पर स्थित हैं।
3. मध्यांक की गणना क्रमीय स्तर (Ordinal level) के लिए सर्वाधिक उपयुक्त है।
4. वितरण के सिरों पर स्थित प्राप्तांक, मध्यांक के मान को कम प्रभावित करते हैं।
5. मध्यांक की मानक त्रुटि (Standard Error); मध्यमान की मानक त्रुटि से अधिक किन्तु बहुलक की मानक त्रुटि से कम होती है।

मध्यांक को ज्ञात करना।

मध्यांक की गणना भी ‘आँकड़ों की प्रकृति के अनुसार की जाती है। अव्यवस्थित तथा व्यवस्थित आँकड़ों के मध्यांक को ज्ञात करने की प्रक्रिया का विवरण निम्नलिखित है –

(I) अव्यवस्थित ऑकों का मध्यांक (The Medium of Ungrouped Data) – अव्यवस्थित आँकड़ों का मध्यांक निकालने के लिए निम्नलिखित बातों का ध्यान देते हैं –

(1) सर्वप्रथम अव्यवस्थित आँकड़ों को आरोही क्रम (Ascending Order) या अवरोही क्रम (Descending Order) में रखते हैं।
(2) N की संख्या ज्ञात करके उसमें 1 जोड़ देते हैं और योग को 2 से भाग देकर भागफल निकाल लेते हैं।
(3) भागफल की संख्या वाला पद/स्थान मध्यांक है जिसकी गिनती किसी भी छोर से की जा सकती है।

11 का विस्तार 10.5 से लेकर 11.5 तक है तथा वर्ग-विस्तार (10.5-11.5) का मध्य-बिन्दु 11 है; अतः मध्यांक =11

(II) व्यवस्थित आँकड़ों का मध्यांक (The Median of Grouped Data) – व्यवस्थित या वर्गीकृत आँकड़ों का मध्यांक ज्ञात करने के लिए निम्नलिखित पदों का अनुसरण करना चाहिए –

1. सर्वप्रथम आवृत्ति वितरण तालिका से दी गयी आवृत्तियों को संचयी आवृत्तियों में बदल लेना चाहिए ताकि यह पता लग सके कि मध्यांक किस वर्गान्तर में है।
2. इस भाँति उस वर्ग को ज्ञात किया जाता है जिसमें आवृत्तियों के योग के आधार ()[latex]\frac { N }{ 2 } [/latex] स्थित हो। इसे मध्यांक वर्ग कहते हैं।
3. मध्यांक वर्ग ज्ञात करने के बाद ‘F’, ‘fm’ तथा ” संकेतों के मूल्य ज्ञात करके प्राप्त मूल्यों को निम्नलिखित सूत्र में स्थापित कर मध्यांक की गणना कर लेनी चाहिए –

हल – प्रश्न में मध्यांक वह बिन्दु होगा जिसके ऊपर ([latex]\frac { 24 }{ 2 } [/latex]) = 12 प्राप्तांक हों। अवलोकन से ज्ञात होता है कि मध्यांक मान 30-39 वाले वर्ग में स्थित है जिसके सम्मुख संचयी आवृत्ति 14 लिखी है।

विशेष परिस्थितियाँ – आवृत्ति वितरण में मध्यांक की गणना करते समय कुछ विशेष परिस्थितियाँ भी उपस्थित हो सकती हैं जो इस प्रकार हैं –

(i) यदि आवृत्ति वितरण में f का मान °0 दिया गया हो यानी आवृत्ति वितरण के ठीक मध्य में एक अन्तराल (Gap) हो तो मध्यांक की गणना का सूत्र होगा –

उदाहरण 6 – में 22-24 वर्गान्तर की आवृत्ति ‘0’ है यानी वितरण के ठीक मध्य में एक अन्तराल (Gap) है; अतः यहाँ सूत्र Md = [latex]\frac { L+U }{ 2 } [/latex] प्रयुक्त होगा।

उदाहरण 7 – में तीन क्रमागत वर्गान्तरों (85-89), (80-84), (75-79) की आवृत्ति ‘0’ दिखायी दे रही है। वितरण में कुल वर्गान्तरों की संख्या 9 है। यहाँ मध्य का वर्गान्तर 80-84 है; अतः =795 और U = 84.5।

प्रश्न 10.
‘बहुलाक या ‘भूयिष्क (Mol) का अर्थ स्पष्ट कीजिए तथा परिभाषा निर्धारित कीजिए। बहुलाक की विशेषताओं का उल्लेख करते हुए इसकी गणना की प्रक्रिया को भी स्पष्ट कीजिए।
या
बहुलक किसे कहते हैं?
उत्तर :
बहुलांक (Mode) को हिन्दी में भूयिष्ठक’ भी कहते हैं। यह वह मूल्य या बिन्दु है जिसकी अधिकतम आवृत्ति होती है। सबसे अधिक घनत्व वाले बिन्दु को भी बहुलोक कहते हैं। इस प्रकार से वह मूल्य जिसके आसपास सर्वाधिक श्रेणियाँ केन्द्रित हों बहुलांक कहलाएगा।

उदाहरण 1 – मान लीजिए हमने किसी कक्षा के 15 छात्रों का भार ज्ञात किया जो किग्रा में निम्न प्रकार है –

हल – इस सारणी में 15 छात्रों में से 6 छात्र ऐसे हैं जिनका भार 51 किग्रा है अर्थात् सर्वाधिक आवृत्ति 51 किग्रा है अर्थात् इन आँकड़ों का बहुलांक 51 किग्रा है।

निष्कर्षतः, सांख्यिकीय आँकड़ों में जिस पद की आवृत्ति अधिकतम हो वह पद बहुलांक कहलाता है।

बहुलांक की परिभाषा
(Definition of Mode)

‘बहुलांक’ को अंग्रेजी में ‘Mode’ कहा गया है। ‘Mode’ शब्द की व्युत्पत्ति फ्रेंच भाषा के ‘la mode’ से हुई है जिसका अर्थ फ्रेंच में फैशन या ‘रिवाज से लिया जाता है। जो वस्तु या मूल्य सर्वाधिक फैशन या चलन में होता है, बहुलांक कहलाती है। उदाहरण के लिए—जूते की दुकान पर उस माप के जूते सबसे ज्यादा संख्या में होंगे जो सबसे ज्यादा लोगों की माप है। इसी भाँति, कपड़े की दुकान पर उस माप के कपड़े अधिक संख्या में होंगे जो अधिकांश लोगों की माप है। यह माप ही बहुलांक है। बहुलांक को Mo से प्रदर्शित किया जाता है।

बहुलांक को निम्नलिखित रूप में परिभाषित किया जा सकता है –

1. गिलफोर्ड के अनुसार, “किसी वितरण में वह बिन्दु, जिसकी आवृत्ति सर्वाधिक हो, बहुलांक कहलाता है।
2. क्रॉक्सटन ऐवं काउडेन के अनुसार, “एक श्रेणी का बहुलांक वह मूल्य है जिसके निकट श्रेणी की इकाइयाँ अधिक-से-अधिक केन्द्रित होती हैं।”
3. ए० एम० टुटले के मतानुसार, “बहुलांक वह मूल्य है जिसके तुरन्त आस-पास आवृत्ति घनत्व अधिकतम होता है।”

बहुलांक की विशेषताएँ
(Characteristics of Mode)

बहुलांक की प्रमुख विशेषताएँ निम्नलिखित हैं –

1. बहुलांक केन्द्रीय प्रवृत्ति को स्थिर एवं विश्वसनीय मान नहीं है, किन्तु इसकी गणना अन्य केन्द्रीय प्रवृत्ति की मापों की अपेक्षा अधिक सरल है।
2. अव्यवस्थित आँकड़ों में बहुलांक की स्थिति सुनिश्चित नहीं होती; अत: ऐसे समूहों में एक से ज्यादा भी बहुलांक हो सकते हैं।
3. बहुलांक को वर्गीय स्तर (Nominal Level) के प्राप्तांकों की केन्द्रीय प्रवृत्ति का एकमात्र तथा सर्वोच्च प्रतीक माना जाता है। ऐसी दशाओं में यह केन्द्रीय प्रवृत्ति का सबसे अधिक प्रतिनिधित्व करता है।

अव्यवस्थित आँकड़ों का बहुलक ज्ञात करना
(The Mode of Ungrouped Data)

अव्यवस्थित आँकड़ों में बहुलांक वह प्राप्तांक होता है जो सबसे अधिक बार दोहराया गया हो, अर्थात् जिसकी आवृत्ति सबसे अधिक हो।

उदाहरण 2 – एक मनोवैज्ञानिक प्रयोग में निम्नलिखित त्रुटियाँ प्राप्त हुई, इनका बहुलक ज्ञात कीजिए –

हल – निरीक्षण से ज्ञात होता है कि 13 अंक 3 बार दोहराया गया है, जो सबसे अधिक है अर्थात् इसकी आवृत्ति 3 है। अतः अभीष्ट बहुलांक 3 होगा।

व्यवस्थित आँकड़ों का बहुलांक
(The Mode of Grouped Data)

व्यवस्थित आँकड़ों का बहुलक ज्ञात करने के प्रमुख दो सूत्र हैं –

इस सूत्रे से बहुलांक की गणना के लिए पहले मध्यमान ज्ञात किया जाता है फिर मध्यांक। मध्यांक में 3 का गुणा करते हैं तथा मध्यमान में 2 का। पहली संख्या में से दूसरी घटाकर बहुलक ज्ञात कर लेते हैं। इस सूत्र की सहायता से बहुलक का सन्निकट मान प्राप्त होता है।

यहाँ, Mo = बहुलांक (Mode)

L₁ = उस वर्गान्तर की निम्नतम सीमा है जिसमें आवृत्तियों की संख्या सर्वाधिक है,
fa = यह उस वर्ग की आवृत्ति है जो बहुलांक मान वाले वर्ग के पास हो तथा जिसकी निम्नतम सीमा बहुलांक व मान वाले वर्ग की निम्नतम सीमा से अधिक हो (Post-modal Class),
f_b = यह उस वर्ग की आवृत्ति है जो वर्ग बहुलांक मान वाले वर्ग के पास है तथा जिसकी निम्नतम सीमा बहुलांक मान वाले वर्ग की निम्नतम सीमा से कम हो (Pre-Modal Class), तथा
C.I.= वर्गान्तर

उदाहरण 3 – नीचे दी गयी व्यवस्थित अंक सामग्री से बहुलांक की गणना कीजिए –

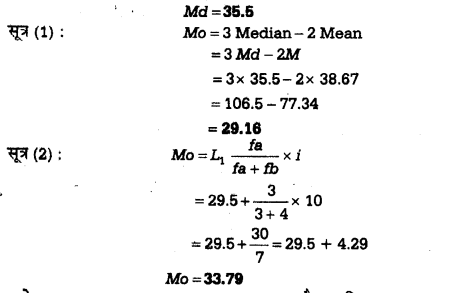
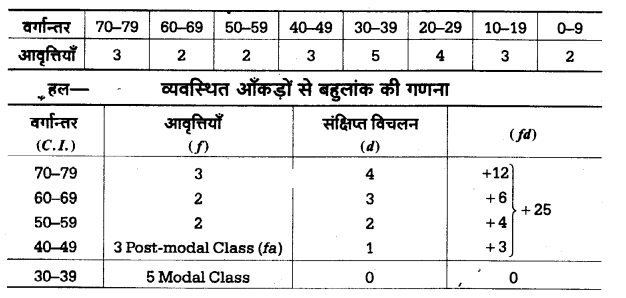
नोट – सूत्र (1) द्वारा ज्ञात Mo का मान 29.16 है, जबकि सूत्र (2) द्वारा ज्ञात Mo को मान 33.79 आता है। दोनों मान भिन्न हैं क्योंकि सूत्र (1) की सहायता से सन्निकट मान प्राप्त होता है।

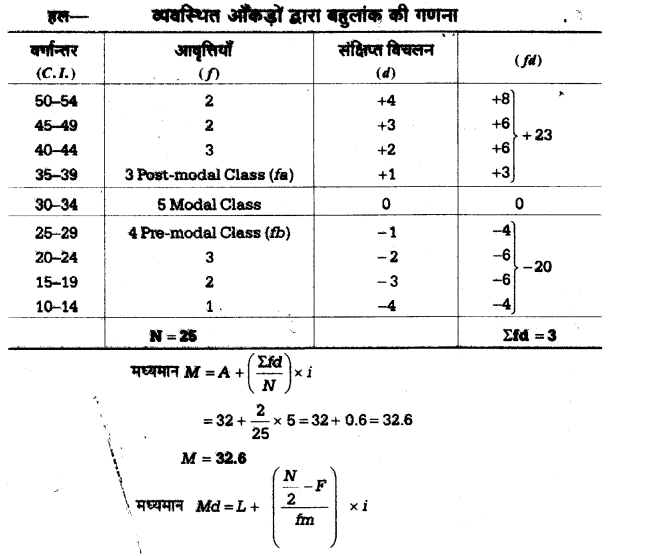
उदाहरण 4 – नीचे दी गयी सारणी की बहुलक मान ज्ञात कीजिए –


मध्यमान, मध्यांक तथा बहुलक पर अभ्यास के लिए कुछ प्रश्न एवं उनके उत्तर,

1. निम्नलिखित आँकड़ों का मध्यमान तथा मध्यांक ज्ञात कीजिए –
5, 6, 6, 4, 7, 9, 10, 15, 13, 22

2. निम्नलिखित प्राप्तांकों का मध्यांक तथा बहुलांक ज्ञात कीजिए –
72, 80, 84, 88, 92, 76, 78,72,74, 72, 80, 62

3. निम्नलिखित व्यवस्थित अंक सामग्री से मध्यमान तथा बहुलांक की गणना कीजिए (N=70) –

4. नीचे दी गयी सारणी का मध्यमान, मध्यांक तथा बहुलांक ज्ञात कीजिए (N = 72) –

5. नीचे दिये गये आवृत्ति वितरण की मदद से केन्द्रवर्ती मान ज्ञात कीजिए (N=84) –

6. निम्न व्यवस्थित आँकड़ों का मध्यमान, मध्यांक व बहुलांक ज्ञात कीजिए –

7. कक्षा 11 के छात्रों की मनोविज्ञान में परीक्षा के प्राप्तांकों का आवृत्ति वितरणनीचे है। इनके द्वारा मध्यमान, मध्यांक तथा बहुलक ज्ञात कीजिए (N=38) –

लघु उत्तरीय प्रश्न

प्रश्न 1.
समंकों (Data) की मुख्य विशेषताओं का उल्लेख कीजिए।
उत्तर :
समंकों की मुख्य विशेषताएँ सांख्यिकी का सम्बन्ध समंकों से होता है। समंकों की मुख्य विशेषताएँ निम्नलिखित हैं –

(1) समंक तथ्यों के समूह होते हैं – इसका अभिप्राय यह है कि किसी एक तथ्य से सम्बन्धित संख्या समंक नहीं कही जा सकती है, क्योंकि एक संख्या से कोई निष्कर्ष नहीं निकाला जा सकता है। उदाहरण के लिए-यदि किसी विद्यार्थी के हिन्दी में प्राप्तांक 40 हैं तो ये प्राप्तांक समंक नहीं कहे जाएँगे, परन्तु यदि उस कक्षा के समस्त विद्यार्थियों के प्राप्तांक दिये हुए हैं तो इन प्राप्तांकों को समंक कहा जाएगा।

(2) समंक संख्याओं के रूप में व्यक्त किये जाते हैं – सांख्यिकी में संख्याओं के रूप में व्यक्त किये गये तथ्य ही समंक कहलाते हैं, न कि गुणात्मक रूप में व्यक्त किये गये तथ्य उदाहरणार्थ–तथ्यों का गुणात्मक रूप; जैसे तीव्र बुद्धि, सामान्य, मन्द बुद्धि समंक नहीं कहलाएँगे; परन्तु यदि इन तथ्यों को हम संख्यात्मक रूप में व्यक्त कर दें तो वे संख्याएँ समंक कही जाएँगी; जैसे-बुद्धि को संख्यात्मक रूप में इस प्रकार व्यक्त किया जाता है –

(3) समंकों के संकलन में उचित शुद्धता होनी चाहिए – समंकों के संकलन में उनकी शुद्धता पर काफी ध्यान देना चाहिए। समंकों की शुद्धता की मात्रा अनुसन्धान के क्षेत्र, उद्देश्य, साधन, समय आदि पर निर्भर करती है।

(4) समंकों को एक-दूसरे से सम्बन्धित रूप में प्रस्तुत किया जाना चाहिए – इसका तात्पर्य यह है कि समंक सजातीय तथा समरूप होने चाहिए, तभी उनकी आपस में तुलना की जा सकती है। जैसे-यदि हम किसी कक्षा के एक विद्यार्थी के गणित में प्राप्तांक लिख लें और दूसरे विद्यार्थी की आयु लिख लें तो इन संख्याओं को हम समंक नहीं कह सकते; क्योंकि इन्हें एक-दूसरे से सम्बन्धित नहीं किया जा सकता। परन्तु यदि दोनों विद्यार्थियों के गणित में प्राप्तांक या दोनों की आयु ही लिखें तो वे समंक कहलाये जा सकते हैं।

(5) समंकों के संकलन का पूर्व-निश्चित उद्देश्य होता है – वे संख्यात्मक तथ्य ही समंक कहे जाएँगे जिनके संकलन का पूर्व-निश्चित उद्देश्य होता है। बिना उद्देश्य के एकत्रित किये गये आँकड़े समंक नहीं बल्कि केवल संख्याएँ ही कहलाते हैं।

(6) समंक अनेक कारणों से पर्याप्त सीमा तक प्रभावित होते हैं – समंकों पर अनेक कारणों को सामूहिक रूप से प्रभाव पड़ता है। कोई एक घटना किसी एक कारण का परिणाम नहीं होती, अपितु अनेक कारणों से प्रभावित होती है। जैसे-यदि हाईस्कूल की परीक्षा में अधिक विद्यार्थियों की प्रथम श्रेणी है तो प्रथम श्रेणी के अनेक कारण हो सकते हैं। हो सकता है विद्यार्थी अधिक संख्या में प्रतिभावान हों, अधिक परिश्रम से पढ़ते हों, निरीक्षक उदार हों आदि।

(7) सर्मक व्यवस्थित रूप से संकलित होते हैं – समंक एकत्रित करने के लिए एक निश्चित योजना तैयार की जाती है तथा उन आँकड़ों का विश्लेषण करके समुचित तथा तर्कसंगत निष्कर्ष निकाले जा सकते हैं। संगणकों को आँकड़े एकत्रित करने के लिए प्रशिक्षण दिया जाता है। समंक प्रश्नावली तथा अनुसूची के अनुसार एकत्र किये जाते हैं।

(8) समंकों को गणना या अनुमान द्वारा संकलित किया जाता है – संमकों को गणना अथवा अनुमान द्वारा एकत्रित किया जाता है। यदि अनुसन्धान का क्षेत्र सीमित है तो गणना द्वारा समंकों का संकलन,किया जा सकता है और यदि क्षेत्र विस्तृत है तो अनुमान द्वारा ही समंकों का संकलन सम्भव है।

प्रश्न 2.
मनोविज्ञान में सांख्यिकी के महत्त्व को स्पष्ट कीजिए।
या
मनोविज्ञान में सांख्यिकीय अध्ययन की कोई चारे उपयोगिताएँ बताइए।
उत्तर :
मनोविज्ञान में सांख्यिकी का महत्त्व

आधुनिक युग में मनोविज्ञान के अध्ययनों में सांख्यिकी का अपना एक विशिष्ट स्थान है। विभिन्न मनोवैज्ञानिक समस्याओं के अध्ययन में सांख्यिकीय विधियों का प्रयोग दिन-प्रतिदिन बढ़ता जा रहा है। सच तो यह है कि मनोवैज्ञानिक सांख्यिकी का प्रयोग अपनी पसन्द या नापसन्द के आधार पर नहीं करता बल्कि आँकड़ों की प्रकृति के कारण सांख्यिकी का प्रयोग उसे अनिवार्य रूप से करना पड़ता है। सांख्यिकीय विधियाँ उपकल्पना की जाँच, व्यक्तिगत विभिन्नताओं के मापन तथा जटिल मानव-व्यवहार को समझने में महत्वपूर्ण भूमिका निभाती हैं। सांख्यिकी के प्रयोग से मनोवैज्ञानिक अध्ययनों के परिणाम निष्पक्ष, विश्वसनीय तथा वैध बन जाते हैं और उनके आधार पर भविष्यवाणियाँ करना सम्भव होता है। मनोविज्ञान में सांख्यिकी का महत्त्व इस प्रकार है

(1) मनोविज्ञान की समस्याओं के अध्ययन में एकत्र किये गये आँकड़े जटिल, अतुलनीय एवं अस्पष्ट होते हैं। सांख्यिकीय विधियों से अव्यवस्थित समंकों को व्यवस्थित रूप में वर्गीकृत करके सारणी, चित्रों व रेखाचित्रों के माध्यम से सरल व बोधगम्य रूप से प्रदर्शित किया जाता है।

(2) मनोवैज्ञानिक प्रयोगों के सम्बन्ध में सांख्यिकी की मदद से वस्तुगत (Objective) तथा शुद्ध (Accurate) परिणाम प्राप्त किये जा सकते हैं।

(3) सांख्यिकीय अध्ययनों से कुछ निष्कर्ष प्राप्त होते हैं जो तथ्यों की वैधानिक व्याख्या कर सकते हैं। सामान्य निष्कर्षों के निर्धारण में भी सांख्यिकी का महत्त्व है; क्योंकि ये निष्कर्ष सांख्यिकीय सूत्रों व नियमों के आधार पर निकाले जाते हैं।

(4) मनोविज्ञान से सम्बन्धित तुलनात्मक अध्ययनों में शुद्ध विश्वसनीय परिणाम निकाले जा सकते हैं। साथ ही तुलना ज्यादा सरल हो जाती है। उदाहरणार्थ-बालकों की बुद्धि की तुलना बुद्धि-लब्धि (1.2.) द्वारा सम्भव है।

(5) सांख्यिकीय अध्ययनों के आधार पर व्यवहार से सम्बन्धित निष्कर्षों के आधार मनोवैज्ञानिक पूर्वकथन या भविष्यवाणी कर सकते हैं।

(6) मनोविज्ञान के क्षेत्र में प्राय: अध्ययन प्रतिदर्श (Sample) पर आधारित होते हैं। प्रतिदर्श समष्टि (Universe) का प्रतिनिधि होता है। सांख्यिकी विधियाँ प्रतिनिधित्वपूर्ण प्रतिदर्श का चयन करने में सहायक हैं।

(7) मनोवैज्ञानिक परीक्षणों के निर्माण में सांख्यिकी का अत्यधिक महत्त्व है। मानसिक व शारीरिक योग्यताओं के मापन हेतु बहुत-से मनोवैज्ञानिक परीक्षण निर्मित होते हैं; उदाहरणार्थ-बुद्धि परीक्षण, व्यक्तित्व परीक्षण तथा रुचि परीक्षण आदि।

स्पष्टत: मेनोविज्ञान के क्षेत्र में सांख्यिकी का विशेष महत्त्व है।

प्रश्न 3.
आँकड़ों के व्यवस्थापन या आवृत्ति वितरण के महत्व को स्पष्ट कीजिए।
उत्तर :
आँकड़ों के व्यवस्थापन यो आवृत्ति वितरण का महत्त्व

आँकड़ों के व्यवस्थापन या आवृत्ति वितरण का महत्त्व निम्नलिखित बिन्दुओं के अन्तर्गत प्रतिपादित किया जा सकता है –

(1) संगृहीत किन्तु अव्यवस्थित आँकड़ों से तत्सम्बन्धी समस्या या अध्ययन विषय के परिणाम के सम्बन्ध में उचित निर्णय लेने में कठिनाई होती है। आँकड़ों को व्यवस्थित करने अर्थात् आवृत्ति वितरण बनाने पर ये ही आँकड़े संक्षिप्त, स्पष्ट तथा बोधगम्य महसूस होते हैं और इनके द्वारा परिणामों के बारे में सरलतापूर्वक उचित निर्णय दिया जा सकता है।

(2) व्यवस्थापन या आवृत्ति वितरण द्वारा सांख्यिकीय आँकड़ों का संक्षिप्त प्रदर्शन सम्भव है। अर्थात् आवृत्ति वितरण आँकड़ों को अर्थपूर्ण बनाने का एक सरल उपाय है। वस्तुतः अव्यवस्थित आँकड़े अर्थहीन होते हैं जिनके गुण-दोषों को सामान्यतः व्यक्ति ग्रहण नहीं कर पाता है। आवृत्ति वितरण तालिका में प्रदर्शित होकर ये ही आँकड़े अर्थपूर्ण बन जाते हैं जिन्हें व्यक्ति सरलता से ग्रहण कर लेता है।

(3) सारणीयन में आवृत्ति वितरण तालिका बनाने के उपरान्त तालिका (Table) का सिर्फ अवलोकन करके ही आँकड़ों का अर्थ ज्ञात किया जा सकता है।

(4) आवृत्ति वितरण तालिका के माध्यम से समान या सजातीय गुण (Homogeneous Characters) पूरी तरह स्पष्ट हो जाते हैं।

(5) आवृत्ति वितरण से आँकड़ों का तुलनात्मक अध्ययन एकदम सरल हो जाता है।

आँकड़ों के व्यवस्थापन या आवृत्ति वितरण के महत्त्व को हम एक उदाहरण के माध्यम से अच्छी प्रकार समझ सकते हैं। मान लीजिए, हमें कक्षा XI के छात्रों की अंक-सूची (Marks-list) प्राप्त है। क्योंकि ये अंक अव्यवस्थित हैं; अतः इनसे परीक्षण के परिणाम के बारे में उचित निर्णय देना दुष्कर होगा। इन प्राप्तांकों को सुव्यवस्थित करैने पर अर्थात् इनका आवृत्ति वितरण तैयार करने पर यही अंक-सूची एक संक्षिप्त, स्पष्ट तथा बोधगम्य स्वरूप में हमारे सामने आ जाएगी। अब हम इसके माध्यम से आसानी से बता पाएँगे कि कितने छात्रों ने प्रथम श्रेणी, कितनों ने द्वितीय और तृतीय श्रेणी प्राप्त की है तथा कितने छात्र परीक्षा में अनुत्तीर्ण हुए हैं।

प्रश्न 4.
केन्द्रीय प्रवृत्ति की माप या सांख्यिकीय माध्य के महत्त्व एवं उपयोगिता का विवरण प्रस्तुत कीजिए।
उत्तर :

केन्द्रीय प्रवृत्ति की माप या सांख्यिकीय माध्य : महत्त्व और उपयोगिता

माध्य के महत्त्व पर प्रकाश डालते हुए प्रो० फिशर ने कहा है कि विशाल संख्यात्मक तथ्यों को समझाने के लिए माध्य बहुत उपयोगी अंक है। सांख्यिकीय में माध्य के अत्यधिक महत्त्व के कारण ही डॉ० बाउले ने तो सांख्यिकी को माध्यों का विज्ञान (Science of Averages) तक कह दिया है। सांख्यिकी विश्लेषण की दूसरी अनेक विधियाँ माध्य पर ही अवलम्बित हैं।

व्यक्तिगत इकाइयों का सांख्यिकी में कोई महत्त्व या उपयोगिता नहीं है किन्तु माध्यों के द्वारा सभी इकाइयों की सामूहिक विशेषताओं व लक्षणों को आसानी से प्रकट किया जा सकता है। इसी प्रकार एक व्यक्ति की आये या आयु का कोई महत्त्व नहीं है, किन्तु सम्पूर्ण समाज की औसत आय या आयु का अत्यधिक महत्त्व है। इस तरह माध्य का समाज में अत्यधिक महत्त्वपूर्ण स्थान है। माध्य के महत्त्व पर प्रो० टिप्पेट ने इस प्रकार प्रकाश डाला है—“माध्य की अपनी सीमाएँ (कमियाँ)होती हैं, किन्तु यदि उनको स्वीकार किया जाए तो कोई भी एक सांख्यिकीय संख्या माध्य से अधिक उपयोगी नहीं होती है।”

गैरेट (H.E. Garrett) ने केन्द्रीय प्रवृत्ति की मापों का महत्त्व इस प्रकार प्रतिपादित किया है –

1. केन्द्रीय प्रवृत्ति की माप समूह के प्राप्तांकों का प्रतिनिधित्व करती है।
2. यह समूचे समूह के गुणों को संक्षेप में प्रदर्शित कर देती है।
3. इसकी सहायता से दो या दो से अधिक समूह के कार्यों एवं गुणों का बोध व उनकी तुलना आसानी से की जा सकती है।
4. इनके द्वारा ढेर सारे प्राप्तांकों के अर्थ को सिर्फ कुछ अंकों या शब्दों द्वारा स्पष्ट किया जा सकता है।
5. प्रामाणिक विचलन (Standard Deviation) तथा सह-सम्बन्ध (Correlation) जैसे उच्च सांख्यिकीय विश्लेषण में केन्द्रीय प्रवृत्ति की माप आवश्यक होती है।
6. उच्च सांख्यिकीय अध्ययनों में केन्द्रीय प्रवृत्ति की माप का प्रयोग प्राथमिक सांख्यिकीय विधियों के रूप में किया जाता है।

प्रश्न 5.
केन्द्रीय प्रवृत्ति की मापों या सांख्यिकी माध्य की प्रमुख विशेषताओं एवं गुणों का उल्लेख कीजिए।
उत्तर :

केन्द्रीय प्रवृत्ति की मापों या सांख्यिकीय माध्य की
प्रमुख विशेषताएँ एवं गुण

‘केन्द्रीय प्रवृत्ति की मापों का आदर्श माध्य में निम्नलिखित विशेषताएँ तथा गुण अनिवार्य रूप से होने चाहिए –

(1) सरल – एक अच्छी माध्य वही हो सकता है जो समझने तथा गणना करने में सरल हो। इससे उसका उपयोग व्यापक रूप में किया जा सकती है।

(2) स्पष्टता और निश्चितता – माध्य की परिभाषा स्पष्ट होनी चाहिए। उसकी कितनी ही बार गणना की जाये, उसका मान हमेशा ही समान आना चाहिए। अनुसन्धानकर्ता के अनुमान की गुंजाइश नहीं रहनी चाहिए। परिभाषा में भिन्न-भिन्न अर्थ न निकले।।

(3) प्रतिनिधित्व – माध्य ऐसा होना चाहिए कि समंक माला अर्थात् समूह के प्रमुख-प्रमुख लक्षण उसमें दिखाई दें। समग्र के प्रत्येक पद में उसके निकट रहने की प्रवृत्ति दिखलाई दे।

(4) बीजगणितीय क्रियाओं के योग्य – माध्य ऐसा हो कि उससे बीजगणितीय क्रियाएँ अर्थात् । जोड़, बाकी, गुणा एवं भाग आसानी से की जा सकें।

(5) माध्ये एक निरपेक्ष संख्या होनी चाहिए – माध्यम समंक माला की संख्याओं में हो,.न कि प्रतिशत या दूसरे सापेक्ष रूप में।

(6) न्यादर्श में परिवर्तन से माध्य बहुत कम प्रभावित हो। न्यादर्श के बदल जाने से माध्य में परिवर्तन न हो या क-से-कम हो। समग्र में से एक तरीके से अनेक न्यादर्श चुने जाये जिनके माध्य लगभग समान हों।

(7) समंक माला के सभी पदों पर आधारित होना चाहिए – माध्य किसी एक पद पर आधारित न हो, तभी माध्य समग्र का प्रतिनिधित्व कर सकता है।

(8) माध्ये सीमान्त पदों से अधिक प्रभावित नहीं होना चाहिए, वह सभी पदों पर आधारित हो।

प्रश्न 6.
केन्द्रीय प्रवृत्ति की मापों या सांख्यिकीय माध्य की सीमाओं या दोषों का उल्लेख कीजिए।
उत्तर :
केन्द्रीय प्रवृत्ति की मापों या सांख्यिकीय माध्य की सीमाएँ या दोष

केन्द्रीय प्रवृत्ति की माप या सांख्यिकीय माध्य की प्रमुख सीमाएँ या दोष निम्नलिखित हैं –

1. सांख्यिकीय माध्य से सिर्फ समूह के गुणों, कार्यों तथा विशेषताओं को ही समझा जा सकता है, ये व्यक्तिगत विशेषताओं का वर्णन नहीं करते।
2. यदि समूह के गुणों, कार्यों तथा विशेषताओं में विषमता पायी जाये तो उस दशा में सांख्यिकी माध्य समूह की प्रतिनिधित्व नहीं करते, जिसका परिणाम यह होता है कि उच्च सांख्यिकीय विश्लेषण के दौरन दूषित और भ्रामक निष्कर्ष निकलते हैं।
3. अलग-अलग तरह के सांख्यिकी विश्लेषण में सांख्यिकीय माध्य के अलग-अलग मापक भिन्न परिणाम प्रस्तुत करते हैं।

प्रश्न 7.
केन्द्रीय प्रवृत्ति की माप या सांख्यिकीय माध्य के विभिन्न प्रकारों का उल्लेख कीजिए तथा इनका तुलनात्मक विवरण प्रस्तुत कीजिए।
उत्तर :
केन्द्रीय प्रवृत्ति की माप या सांख्यिकीय माध्य के प्रकार

सांख्यिकी में माध्य कई प्रकार के होते हैं जिनमें से प्रमुख माध्ये निम्नलिखित हैं –

1. मध्यमान (Mean)
2. मध्यांक माने (Median) तथा
3. बहुलांक मान (Mode)।

केन्द्रीय प्रवृत्ति की विभिन्न मापों की तुलना

मध्यमान, मध्यांक और बहुलांक – केन्द्रीय प्रवृत्ति की इन तीन मापों में समानता या विषमता, आवृत्ति वितरण की प्रकृति पर निर्भर है। इस विषय में निम्नलिखित दशाएँ अनुभव में आती हैं –

(1) सममित (Symmetrical) आवृत्ति वितरण की स्थिति में मध्यमान, मध्यांक तथा बहुलक तीनों को मान समान आता है।
(2) विषमता (Skewness) आवृत्ति वितरण होने पर इन तीनों अर्थात् मध्यमान, मध्यांक तथा बहुलक के मान भिन्न-भिन्न आते हैं। यहाँ दो स्थितियाँ सम्भव हैं –
(a) धनात्मक विषमता (Positively Skewed Distribution) में मध्यमान का मूल्य कम, मध्यांक को मध्यमान से अधिक तथा बहुलांक का मध्यांक से भी अधिक होता है।
(b) ऋणात्मक विषमता (Negatively Skewed Distribution) में मध्यमान का मान सबसे अधिक, मध्यांक का मान उससे कम तथा बहुलांक का मान सबसे कम होता है।
(3) मध्यमान सबसे अधिक शुद्ध, मध्यांक अपेक्षाकृत कम शुद्ध तथा बहुलांक सबसे कम शुद्ध मान स्वीकार किये गये हैं।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
सांख्यिकी की परिभाषा दीजिए।
उत्तर :
प्रो० सेलिगमैन ने सांख्यिकी की एक स्पष्ट परिभाषा इन शब्दों में प्रतिपादित की है, सांख्यिकी वह विज्ञान है जो किसी भी अनुसन्धान (जाँच) के क्षेत्र पर प्रकाश डालने के लिए संख्यात्मक आंकड़ों का संग्रहण, प्रस्तुतीकरण, वर्गीकरण, तुलना तथा निर्वचन की रीतियों का प्रयोग करता है।”

प्रश्न 2.
सांख्यिकी की किन्हीं दो विशेषताओं के बारे में लिखिए।
उत्तर :

1. सांख्यिकी विज्ञान तथा कला दोनों है।
2. सांख्यिकी में किसी अनुसंधान क्षेत्र से सम्बन्धित सामूहिक संख्यात्मक तथ्यों के संकलन, प्रदर्शन, विश्लेषण तथा निर्वचन की रीतियों का विधिवत् अध्ययन किया जाता है।

प्रश्न 3.
सांख्यिकी की मुख्य सीमाओं का उल्लेख कीजिए।
उत्तर :
यह सत्य है कि सांख्यिकी की अत्यधिक उपयोगिता एवं महत्त्व है, परन्तु इसकी कुछ सीमाएँ भी हैं। सर्वप्रथम हम कह सकते हैं कि सांख्यिकी के माध्यम से केवल संख्यात्मक तथ्यों का अध्ययन किया जा सकता है, इसके माध्यम से गुणात्मक तथ्यों का अध्ययन नहीं किया जा सकता। इसी प्रकार सांख्यिकी के माध्यम से विजातीय तथ्यों का अध्ययन नहीं किया जा सकता है। यही नहीं, इसके माध्यम से केवल समूह का अध्ययन किया जा सकता है, व्यक्ति का नहीं। बिना सन्दर्भ से सांख्यिकी के माध्यम से प्राप्त होने वाले परिणाम असत्य तथा भ्रामक होते हैं। सांख्यिकी के माध्यम से प्राप्त होने वाले परिणाम केवल औसत रूप में ही सही हैं। वास्तव में, सांख्यिकी एक साधन है, साध्य नहीं। इन्हीं सीमाओं को ध्यान में रखते हुए यूल तथा केण्डाल ने कहा है, “सांख्यिकीय राीतियाँ अयोग्य व्यक्तियों के हाथों में खतरनाक औजार हो सकती हैं।”

प्रश्न 4.
प्रदत्त (Data) से क्या आशय है?
उत्तर :
प्रदत्त (Datum) वह तथ्य या सूचना है जिसके आधार पर हम निष्कर्ष निकाल सकते हैं। किसी परीक्षा में प्राप्तांकों को प्रदत्त कहा जा सकता है। यह परीक्षा उनके व्यवहार के किसी भी पहलू से सम्बन्धित हो सकती है। उदाहरण के लिए-यदि कक्षा बारह के छात्रों की मनोविज्ञान विषय में परीक्षा ली जाये तो परीक्षा में छात्रों को जो प्राप्तांक प्राप्त होंगे उन्हें प्रदत्त कहा जाएगा। प्रयोगों, शोध कार्य या सर्वेक्षणों में जो आँकड़े सूचनाएँ एकत्र की जाती हैं, उन्हें भी प्रदत्त कहा जाता है। अंग्रेजी में Data शब्द बहुवचन है जबकि Datum शब्द एकवचन।

प्रश्न 5.
प्राप्तांक (Score) के अर्थ एवं सीमाओं का उल्लेख कीजिए।
उत्तर :
“किसी मनोवैज्ञानिक परीक्षा में प्राप्तांक का अभिप्राय उस इकाई से है जो दो सीमान्तों के बीच होती है। उदाहरणार्थ-किसी छात्र के बुद्धि-परीक्षण में 130 प्राप्तांक का अर्थ दो सीमान्तों 129.5-130.5 में लगाया जाता है। यहाँ 130 प्राप्तांक 129.5-130.5 का मध्य-बिन्दु है।

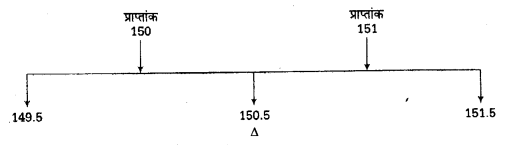
सांख्यिकी में किसी भी प्राप्तांक का विस्तार (Interval) दी गई संख्या से आधा इकाई कम से लेकर आधार इकाई अधिक तक माना जाता है। इस भाँति प्रत्येक प्राप्तांक का प्रसार क्षेत्र (Range) एक के बराबर होता है। किसी प्राप्तांक की दो सीमाएँ हैं—उसकी उच्चतम सीमा (Upper limit) तथा उसकी निम्नतम सीमा (Lower limit)। प्राप्तांक की उच्चतम सीमा ज्ञात करने के लिए उसमें 0.5 जोड़ देना चाहिए तथा निम्नतम सीमा ज्ञात करने के लिए उसमें से 0.5 घटा देना चाहिए। प्राप्तांक 130 से हमारा अभिप्राय- 129.5 से लेकर 130.5 तक है तथा प्राप्तांक 130 का मान इन दोनों सीमाओं के मध्य कोई भी हो सकता है। 130.5 इस प्राप्तांक की उच्चतम सीमा तथा 129.5, इसकी निम्नतम सीमा है। प्राप्तांक 150 की उच्चतम सीमा 150 + 0.5 अर्थात् 15.5 तथा निम्नतम सीमा 150-0.5 = 149.5 होगी।। इसी भाँति 151 प्राप्तांक की निम्नतम सीमा 150.05 तथा उच्चतम सीमा 151.5 होगी। इसे निम्नलिखित रूप में प्रदर्शित कर सकते हैं –

प्रश्न 6.
सांख्यिकी में प्रसार क्या है?-एक उदाहरण दीजिए।
उत्तर :
सांख्यिकी में प्राप्तांकों में परिवर्तनशीलता की मापों को ज्ञात किया जाता है। परिवर्तनशीलता की एक माप को प्रसार (Range) कहा जाता है। यह परिवर्तनशीलता की एक स्थल माप है। जब किसी अध्ययन के दौरान अध्ययनकर्ता के पास कम समय होता है तथा वह प्राप्तांकों के विवरण की परिवर्तनशीलता को जानना चाहता है तो उस स्थिति में विवरण के प्रसार को ज्ञात करने का प्रयास किया जाता है। नियमानुसार प्रसार को निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है –
प्रसार (Range)= (उच्चतम प्राप्तांक-न्यूनतम प्राप्तांक) +1
उदाहरण-उच्चतम प्राप्तांक 80, न्यूनतम प्राप्तांक 5
प्रसार = (80 – 5) + 1 = 76

प्रश्न 7.
मध्यमान (Mean) की मुख्य विशेषताओं का उल्लेख कीजिए। [2016]
उत्तर :
मध्यमान में निम्नलिखित विशेषताएँ होती हैं –

1. मध्यमान दिये गये वितरण का केन्द्र या सन्तुलन बिन्दु होता है।
2. मध्यमान की स्थिति वितरण के प्रत्येक प्राप्तांक से प्रभावित होती है। उदाहरणार्थ—प्राप्तांकों में से किसी प्राप्तांक को घटाने या बढ़ाने पर वितरण का मध्यमान भी घट या बढ़ जाएगा।
3. वितरण के सभी प्राप्तांकों को एक निश्चित संख्या से गुणा करने पर मध्यमान का मान उस संख्या के गुणनफल के बराबर हो जाएगा।
4. केन्द्रीय प्रवृत्ति के मापों में मध्यमान एक निष्पक्ष (Unbiased) सांख्यिकी है जिसमें मानक त्रुटि (Standard Error) कम होती है।

प्रश्न 8.
मध्यसान के मुख्य गुणों का उल्लेख कीजिए।
उत्तर :
मध्यमान के मुख्य गुण निम्नलिखित हैं –

1. केन्द्रीय प्रवृत्ति की मापों में सर्वाधिक शुद्ध माप मध्यमान है।
2. यह सबसे अधिक विश्वसनीय सांख्यिकी है।
3. इसकी गणना शीघ्र तथा सरलता से हो जाती है।
4. मध्यमान वितरण के प्राप्तांकों का विशुद्ध प्रतिनिधित्व करता है।
5. केन्द्रीय प्रवृत्ति की अन्य मापों की अपेक्षा मध्यमान की मदद से तुलना करना अधिक सरल
6. प्रामाणिक विचलन तथा सहसम्बन्ध गुणांक जैसी सांख्यिकी गणनाओं में मध्यमान की गणना जरूरी है।

प्रश्न 9.
मध्यमान के मुख्य दोषों का उल्लेख करते हुए स्पष्ट कीजिए कि इसका प्रयोग कब उचित होता है?
उत्तर :
मध्यमान के कुछ दोष ये हैं –

1. मुक्त सिरों वाले या अपूर्ण प्राप्तांक वितरण के अन्तर्गत मध्यमान प्रयोग नहीं किया जा सकता।
2. इसी प्रकार असामान्य अंक-वितरण के अन्तर्गत भी मध्यमान की जगह मध्यांक का प्रयोग उचित समझा जाता है।

मध्यमान का प्रयोग कब और कहाँ करना उचित है, इसके लिए कुछ निर्देश नीचे दिये जा रहे

1. सबसे अधिक शुद्ध एवं विश्वसनीय केन्द्रीय प्रवृत्ति ज्ञात करने हेतु मध्यमान का प्रयोग किया जाता है।
2. जब बहुलांक, प्रामाणिक विचलन तथा सहसम्बन्ध आदि की गणना करनी हो, तब भी मध्यमान की गणना आवश्यक होती है।
3. सामान्य वितरण (अर्थात् जब दिये गये प्राप्तांकों के सभी अंक समान रूप से वितरित हों) के अन्तर्गत भी मध्यमान प्रयुक्त होती है।
4. मध्यमान की गणना तुलनात्मक अध्ययन के समय भी आवश्यक होती है।

प्रश्न 10.
मध्यांक (Median) के मुख्य गुणों का उल्लेख कीजिए।
उत्तर :
मध्यांक के मुख्य गुण निम्नलिखित हैं –

1. सरलता – मध्यांक को ज्ञात करना तथा इसे समझना दोनों ही बहुत आसान हैं।
2. चरम मूल्यों से अप्रभावित – मध्यांक के मूल्य पर श्रेणी के सबसे बड़े या छोटे मूल्य का कोई प्रभाव नहीं पड़ता है।
3. गुणात्मक विशेषताओं के अध्ययन में उपयोगी – गुणात्मक तथ्य; जैसे-बुद्धिमत्ता, स्वास्थ्य, ईमानदारी, गरीबी आदि के निर्धारण में यह अति उपयोगी होता है।
4. निश्चितता – मध्यांक का मूल्य बहुलांक की भाँति अस्पष्ट और अनिश्चित नहीं होता है।
5. अधूरे समंक से मध्यांक निर्धारण सम्भव है। केवल मध्यांक वर्ग तथा कुछ दूसरी सूचनाएँ मिल जाने पर ही इसको ज्ञात कर सकते हैं। सम्पूर्ण पदमाला की जानकारी जरूरी नहीं।
6. इसको बिन्दुरेख विधि से भी ज्ञात कर सकते हैं। निरीक्षण से भी मध्यांक का निर्धारण किया जा सकता है।

प्रश्न 11.
मध्यांक (Median) के मुख्य दोषों या सीमाओं का उल्लेख कीजिए।
उत्तर :
मध्यांक के मुख्य दोष या सीमाएँ निम्नलिखित हैं –

1. सीमान्त मूल्यों की उपेक्षा – सामान्यत: मध्यांक निर्धारण में श्रेणी के सीमान्त पदों पर ध्यान नहीं दिया जाता है। इस तरह मध्यांक में सभी पदों को समान महत्त्व नहीं देते हैं।
2. आवश्यक क्रियाएँ – श्रेणी को आरोही या अवरोही आधार पर व्यवस्थित करने का कार्य अनिवार्य रूप से करमा पड़ता है।
3. निर्धारण में कठिनाई – यदि मध्य पद दो मूल्यों के बीच आता है, तब मध्यांक मूल्य बिल्कुल ठीक नहीं होता है। केन्द्रीय मूल्यों के औसत को मध्यांक लिया जाता है। इसी तरह सतत श्रेणी में भी यह इस मान्यता पर आधारित है कि प्रत्येक वर्ग में आवृत्तियाँ समान हैं।
4. कभी-कभी मध्यांक एक प्रतिनिधि माप नहीं होता है विशेषकर पदों की संख्या कम होने पर।
5. मध्यांक बीजगणितीय विवेचन में अनुपयोगी रहता है। मध्यांक मूल्य को पदों की संख्या से गुणा करने पर पदों के मूल्यों का योग मालूम नहीं कर सकते हैं।

प्रश्न 12.
मध्यांक के उचित प्रयोग सम्बन्धी कुछ निर्देश दीजिए।
उत्तर :
मध्यांक के उचित प्रयोग हेतु निम्नलिखित निर्देश दिये जा सकते हैं –

1. मध्यांक की गणना असामान्य वितरण की स्थिति में करनी चाहिए जबकि अंक सामग्री का वास्तविक मध्य-बिन्दु पता लगाना हो।
2. श्रेणी के शुरू तथा अन्तर के अंक जब मध्यमान को प्रभावित करते हों तब भी मध्यांक की गणना की जाती है। उदाहरणार्थ – 2, 3, 4, 5, 6 का मध्यमान (M) तथा मध्यांक (Md) 4 है। यदि 6 के स्थान पर 11 हो तो मध्यांक 4 ही रहेगा लेकिन मध्यमान 5 हो जाएगा।
3. इसकी गणना उस समय की जानी उचित है जबकि अपेक्षाकृत कम शुद्ध केन्द्रीय प्रवृत्ति के मान की आवश्यकता हो।
4. बहुलांक (Mode) की गणना के समय भी मध्यांक ज्ञात किया जाता है।

प्रश्न 13.
बहुलांक (Mode) के मुख्य गुणों का उल्लेख कीजिए।
उत्तर :
बहुलांक के प्रमुख गुण निम्नलिखित हैं –

1. निर्धारण में सरलता—इसको निरीक्षण अर्थात् देखकर भी तय किया जा सकता है।
2. बिन्दुरेखीय विधि से भी इसका निर्धारण कर सकते हैं।
3. प्रतिनिधित्व-बहुलांक मूल्य श्रेणी का सबसे श्रेष्ठ प्रतिनिधि माना जाता है।
4. सीमान्त पदों का कोई प्रभाव नहीं पड़ता है।
5. उद्योग, व्यापार एवं वाणिज्य में इसका बहुत उपयोग होता है। विशेषकर जूते निर्माताओं, सिले-सिलाये वस्त्र तैयार करने वालों आदि के लिए यह बहुत उपयोगी है।

प्रश्न 14.
बहुलांक (Mode) के मुख्य दोषों का उल्लेख कीजिए।
उत्तर :
बहुलांक के मुख्य दोष निम्नलिखित हैं –

1. समान आवृत्तियाँ होने पर इसका निर्धारण कठिन हो जाता है।
2. सीमान्त मूल्यों की अवहेलना होती है।
3. बीजगणितीय विश्लेषण सम्भव नहीं है।
4. श्रेणी के सभी पदों पर आधारित नहीं होता है।
5. श्रेणी में कभी-कभी बहुलांक भ्रमात्मक होता है।

प्रश्न 15.
बहुलांक (Mode) का प्रयोग किन परिस्थितियों में किया जाना चाहिए?
उत्तर :

बहुलांक का प्रयोग निम्नलिखित परिस्थितियों में करना वांछित है –

1. सबसे कम शुद्ध केन्द्रीय प्रवृत्ति के मान की गणना के समय बहुलांक का प्रयोग उचित है।
2. यदि निरीक्षण-मात्र से ही केन्द्रीय प्रवृत्ति की गणना करनी हो तो बहुलक उपयोगी है।
3. वितरण के कुछ वर्ग या अंक छूटे होने पर भी बहुलांक का प्रयोग उचित है।
4. व्यापार में अधिक प्रचलित वस्तु या लोकप्रिय फैशन से जुड़ी समस्या के अध्ययन में बहुलांक का सर्वाधिक प्रयोग होता है।

निश्चित उत्तरीय प्रश्न

प्रश्न I.
निम्नलिखित वाक्यों में रिक्त स्थानों की पूर्ति उचित शब्दों द्वारा कीजिए –

1. बहुवचन में सांख्यिकी शब्द का अर्थ ………………….. से है, जो किसी विशिष्ट क्षेत्र से सम्बन्धित संख्यात्मक तथ्य होते हैं।
2. ………………….. प्रदत्तों के संग्रह, उनके विश्लेषण तथा निष्कर्ष निकालने का विज्ञान है।
3. सांख्यिकी में संख्याओं के रूप में व्यक्त किये गये तथ्य ही ………………….. कहलाते हैं।
4. मनोविज्ञान के क्षेत्र में तुलनात्मक अध्ययन करने में सांख्यिकी ………………….. होती है।
5. सांख्यिकी केवल संख्यात्मक तथ्यों का अध्ययन करती है, ………………….. का नहीं।
6. सांख्यिकी द्वारा केवल ………………….. तथ्यों का ही अध्ययन किया जा सकता है।
7. सांख्यिकी अपने आप में एक साधन है, ………………….. नहीं।
8. संकलित आँकड़ों को जब एक निश्चित क्रम में लिखा जाता है तो इस भाँति बनी हुई पदमाला या श्रृंखला को ………………….. कहा जाता है।
9. दिये गये प्रदत्तों के उच्चतम एवं न्यूनतम अंकों के अन्तर को ………………….. कहते हैं।
10. आँकड़ों को समानता या सजातीयता के आधार पर वर्गों में व्यवस्थित करने को ………………….. कहते हैं।
11. किसी प्राप्तांक के बार-बार आने की प्रवृत्ति को ………………….. कहते हैं।
12. केन्द्रीय प्रवृत्ति की माप समूह के प्राप्तांकों का ………………….. करती है।
13. अव्यवस्थित सांख्यिकीय आँकड़ों को व्यवस्थित करके मध्यमान की गणना हेतु ………………….. निर्धारित किया जाता है।
14. किसी कक्षा के बच्चों के प्राप्तांकों को जोड़कर बच्चों की कुल संख्या से भाग देने पर जो मान प्राप्त होता है, उसे ………………….. कहते हैं।
15. केन्द्रीय प्रवृत्ति की मापों में सर्वाधिक शुद्ध माप ………………….. है।
16. सांख्यिकी में दिये गये प्राप्तांकों को ठीक दो बराबर भागों में बांटने वाले बिन्दु को ………………….. कहते हैं।
17. आरोही अथवा अवरोही क्रम में लिखे पदों के मध्य पद के रूप को ………………….. कहते हैं।
18. किसी दी गयी पदमाला में सर्वाधिक बार आने वाले मूल्य को ………………….. कहते हैं।
19. बहुलांक में श्रेणी के सीमान्त मूल्यों की ………………….. होती है।

उत्तर :

1. सर्मकों या आंकड़ों
2. सांख्यिकी
3. समंक
4. सहायक
5. गुणात्मक तथ्यों
6. सजातीय
7. साध्य
8. सांख्यिकी श्रेणी
9. वर्ग विस्तार
10. वर्गीकरण
11. केन्द्रीय प्रवृत्ति
12. प्रतिनिधित्व
13. कल्पित मध्यमान
14. मध्यमान
15. मध्यमान
16. मध्यांक
17. मण्यांक
18. पुलकि
19. अपहेलना।

प्रश्न II
निम्नलिखित प्रश्नों का निश्चित उत्तर एक शब्द अथवा एक वाक्य में दीजिए।

प्रश्न 1.
शाब्दिक रूप से सांख्यिकी (Statlalc) का अर्थ स्पष्ट कीजिए।
उत्तर :
सांख्यिकी’ शब्द दो अर्थों में प्रयोग होता है। एकवचन के अर्थ में ‘सांख्यिकी का प्रयोग एक विज्ञान के रूप में किया जाता है। बहुवचन के अर्थ में सांख्यिकी का प्रयोग आँकड़ों, संख्याओं या समंकों के रूप में लिया जाता है।

प्रश्न 2.
सांख्यिकी के सन्दर्भ में समंकों की दो विशेषताओं का उल्लेख कीजिए।
उत्तर :

1. समंक तथ्यों के समूह होते हैं तथा
2. समंक संख्याओं के रूप में व्यक्त किये जाते हैं।

प्रश्न 3.
एक विज्ञान के रूप में सांख्यिकी की उचित परिभाषा लिखिए।
उत्तर :
लाविट के अनुसार, “सांख्यिकी वह विज्ञान है जो संख्यात्मक तथ्यों के संग्रह, वर्गीकरण तथा सारणीयन से सम्बन्ध रखता है, जिससे उन्हें घटनाओं की व्याख्या, विवरण और तुलना के लिए प्रयुक्त किया जा सके।

प्रश्न 4.
सांख्यिकी की प्रकृति क्या है?
उत्तर :
सांख्यिकी विज्ञान तथा कला दोनों है। इसमें किसी अनुसन्धान क्षेत्र से सम्बन्धित सामूहिक संख्यात्मक तथ्यों के संकलन, प्रदर्शन, विश्लेषण तथा निर्वचन की रीतियों का विधिवत् अध्ययन किया जाता है।

प्रश्न 5.
सांख्यिकी के विषय में वॉलिस और “रॉबर्टस का दृष्टिकोण क्या है?
उत्तर :
बॉलिस और रॉबर्ट्स के अनुसार, “सांख्यिकी स्वतन्त्र और मूलभूत ज्ञान का समूह नहीं है अपितु ज्ञान-प्राप्ति की रीतियों का समूह है।”

प्रश्न 6.
‘सांख्यिकीय श्रेणी की एक व्यवस्थित परिभाषा लिखिए।
उत्तर :
कॉनर के अनुसार, “जब दो चल-राशियों के मूल्यों को साथ-साथ इस भाँति व्यवस्थित किया जाये कि एक मापनीय अन्तर दूसरे के मापनीय अन्तर का सहगामी हो तो इस प्रकार से प्राप्त पदमाला को सांख्यिकीय श्रेणी कहते हैं।”

प्रश्न 7.
सांख्यिकीय श्रेणियों के मुख्य प्रकारों का उल्लेख कीजिए।
उत्तर :

(क) व्यक्तिगत श्रेणी
(ख) असतत या खण्डित या, विच्छिन्न श्रेणी तंथा
(ग) सतत या अखण्डित या अविच्छिन श्रेणी।

प्रश्न 8.
वर्गीकरण की एक व्यवस्थित परिभाषा लिखिए।
उत्तर :
कॉनर के अनुसार, “वर्गीकरण तथ्यों को उनकी विशेषताओं अथवा गुणों के आधार पर समूह एवं वर्गों में क्रमबद्ध करने की एक प्रक्रिया है, जिसका उद्देश्य विभिन्नताओं के बीच समान तथ्यों को खोजकर एक साथ रखना है।”

प्रश्न 9.
सारणीयन की परिभाषा लिखिए।
उत्तर :
कॉनर के अनुसार, “सारणीयन किसी विचाराधीन समस्या को स्पष्ट करने के उद्देश्य से किया जाने वाला सांख्यिकी तथ्यों का क्रमबद्ध एवं सुव्यवस्थित प्रस्तुतीकरण है।’

प्रश्न 10.
प्राप्तांकों को समूहबद्ध करने की विधियाँ कौन-कौन सी हैं?
उत्तर :

(क) समावेशी विधि
(ख) शुद्ध वर्गीकृत श्रृंखला विधि तथा
(ग) अपवर्जी विधि।

प्रश्न 11.
केन्द्रीय प्रवृत्ति की माप लिखिए।
उत्तर :

1. मध्यमान, (Mean)
2. मध्यांक (Median) तथा
3. बहुलांक (Mode)

प्रश्न 12.
सांख्यिकीय माध्य या औसत से क्या आशय है?
उत्तर :
वह संख्या, जो किसी समूह-विशेष के सभी आँकड़ों का प्रतिनिधित्व करती है, उस समूह का सांख्यिकी माध्य या औसत कहलाती है।

प्रश्न 13.
मध्यमान (Mean) से क्या आशय है?
उत्तर :
मध्यमान वह मान है जो दिये हुए पदों के योगफल में पदों की संख्या से भाग देने पर प्राप्त होता है।

प्रश्न 14.
अव्यवस्थित प्राप्तांकों से मध्यमान ज्ञात करने का सूत्र लिखिए।
उत्तर :
[latex]{ M= }\frac { \Sigma X }{ N } [/latex]
यहाँ M = मध्यमान, ∑ = प्राप्तांकों का योग, N = प्राप्तांकों की संख्या।

प्रश्न 15.
मध्यांक (Median) से क्या आशय है?
उत्तर :
यदि आँकड़ों को आरोही या अवरोही क्रम में व्यवस्थित किया जाये तो बिल्कुल मध्य में पड़ने वाला आँकड़ा मध्यांक कहलाता है।

प्रश्न 16.
बहुलांक (Mode) से क्या आशय है?
उत्तर :
क्राक्सटन एवं काउडेन के अनुसार, “एक श्रेणी का बहुलांक वह मूल्य है। जिसके निकट श्रेणी की इकाइयाँ अधिक-से-अधिक केन्द्रित होती हैं।”

प्रश्न 17.
शुद्धता के दृष्टिकोण से मध्यमान, मध्यांक और बहुतांक या तुलनात्मक विवरण प्रस्तुत कीजिए।
उत्तर :
परिणामों की शुद्धता के दृष्टिकोण से मध्यमान को सबसे अधिक शुद्ध, मध्यांक को अपेक्षाकृत कम शुद्ध तथा बहुलांक को सबसे कम शुद्ध माना जाता है।

बहुविकल्पीय प्रश्न

प्रश्न 1.
सांख्यिकी का प्रत्यक्ष रूप से सम्बन्ध है –

(क) विज्ञान से
(ख) संख्यात्मक तथ्यों से
(ग) सुझावों एवं संकेतों से
(घ) गुणात्मक तथ्यों से,

प्रश्न 2.
“सांख्यिकी को संख्यात्मक समंकों के एकत्रीकरण, प्रस्तुतीकरण, विश्लेषण तथा निर्वचन के रूप में परिभाषित किया जा सकता है।” प्रस्तुत परिभाषा के प्रतिपादक हैं –

(क) डॉ० बाउले
(ख) पर्सन और हार्लोज
(ग) क्रॉक्सटन और काउडेन
(घ) इनमें से कोई नहीं।

प्रश्न 3.
सांख्यिकी को माना जाता है –

(क) शुद्ध विज्ञान
(ख) शुद्ध कला
(ग) विज्ञान तथा कला दोनों
(घ) इनमें से कोई नहीं।

प्रश्न 4.
मनोविज्ञान में सांख्यिकी की उपयोगिता है –

(क) आँकड़ों को सरल एवं बोधगम्य बनाना
(ख) आँकड़ों को सुस्पष्ट एवं संक्षिप्त प्रस्तुतीकरण
(ग) आँकड़ों के सहसम्बन्ध का वर्णन
(घ) उपर्युक्त सभी

प्रश्न 5.
आँकड़ों के व्यवस्थापन की पद्धति है –

(क) वर्गीकरण
(ख) सारणीयन
(ग) रेखाचित्र प्रस्तुतीकरण
(घ) ये सभी

प्रश्न 6.
प्राप्तांक 76 की न्यूनतम सीमा है – [2014]

(क) 76
(ख) 76.5
(ग) 755
(घ) 75.

प्रश्न 7.
सांख्यिकी में प्राप्तांक 1 का विस्तार होता है – [2011]

(क) 0.0 से 1
(ख) 0.5 से 1
(ग) 0.5 से 1.5
(घ) 1 से 1.5 8.

प्रश्न 8.
आंकड़े 8, 23, 16, 15, 5, 26, 6, 38, 33, 11 एवं 15 का विस्तार है – (2015)

(क) 5
(ख) 6
(ग) 33
(घ) 38

प्रश्न 9.
केन्द्रीय प्रवृत्ति के माप हैं – (2008)

(क) मध्यमान तथा सहसम्बन्ध
(ख) मध्यांक तथा
(ग) बहुलक
(घ) मध्यमान, मध्यांक तथा बहुलक।

प्रश्न 10.
अंक वितरण के सभी अंकों को जोड़कर उनकी संख्या से भाग देने पर जो भागफल प्राप्त होता है, उसे कहते हैं – (2010)

(क) प्रतिशतांक
(ख) मध्येमान
(ग) मध्यांक
(घ) प्रसार

प्रश्न 11.
मध्यमान का गुण है –

(क) सर्वाधिक शुद्ध माप
(ख) शीघ्र एवं सरल गणना
(ग) दिये गये प्राप्तांकों का विशुद्ध प्रतिनिधित्व
(घ) उपर्युक्त सभी

प्रश्न 12.
किसी सांख्यिकीय वितरण में ऊपर-नीचे दो बराबर भागों में बाँटने वाले बीच के अंक को कहते हैं –

(क) मध्यमान
(ख) मध्यांक
(ग) बहुलक
(घ) प्रतिशतांक

प्रश्न 13.
यदि दिये गये आँकड़ों को आरोही या अवरोही क्रम में व्यवस्थित किया जाए तो बिल्कुल मध्य में पड़ने वाला ऑकड़ा कहलाता है – (2007)

(क) मध्यमान
(ख) मध्यांक
(ग) बहुलांक
(घ) इनमें से कोई नहीं।

प्रश्न 14.
मध्यांक का दोष है –

(क) सीमान्त मूल्यों की अपेक्षा
(ख) निर्धारण में कठिनाई
(ग) कम पदों की दशा में सही प्रतिनिधित्व नहीं हो पाता
(घ) उपर्युक्त सभी दोष

प्रश्न 15.
वितरण में जिस अंक की आवृत्ति सर्वाधिक होती है, उसे कहते हैं –

(क) मध्यांक
(ख) बहुलक
(ग) मध्यमान
(घ) चतुर्थांक

प्रश्न 16.
आँकड़े 8, 6, 8, 2, 11, 6, 8 एवं 5 में से है –

(क) मध्यमान
(ख) मानक विचलन
(ग) मध्यांक
(घ) बहुलांक

उत्तर :

1. (ख) संख्यात्मक तथ्यों से
2. (ग) क्रॉक्सटन और काउडन
3. (ग) विज्ञान तथा कला दोनों
4. (घ) उपर्युक्त सभी
5. (घ) ये सभी
6. (ग) 75.57
7. (ख) 0.5 से 1 8.
8. (ग) 33
9. (घ) मध्यमान मध्यांक तथा बहुलेक
10. (ख) मध्यमान
11. (घ) उपर्युक्त सभी
12. (ख) मध्याक
13. (ख) मध्यांक
14. (घ) उपर्युक्त सभी दोष
15. (ख)बहुलक
16. (घ) बहुलाका

We hope the UP Board Solutions for Class 11 Psychology Chapter 12 Statistics in Psychology (मनोविज्ञान में सांख्यिकीय गणना) help you.