UP Board Solutions for Class 12 Economics Chapter 27 Measure of Central Tendency: Arithmetic Mean (केन्द्रीय प्रवृत्ति की माप : समान्तर माध्य)

UP Board Solutions for Class 12 Economics Chapter 27 Measure of Central Tendency: Arithmetic Mean (केन्द्रीय प्रवृत्ति की माप : समान्तर माध्य)

UP Board Solutions for Class 12 Economics Chapter 27 Measure of Central Tendency: Arithmetic Mean (केन्द्रीय प्रवृत्ति की माप : समान्तर माध्य)

विस्तृत उत्तरीय प्रश्न (6 अंक)

प्रश्न 1
समान्तर माध्य से आप क्या समझते हैं ? समान्तर माध्य के प्रकार बताइए। [2010]
उत्तर:
साधारण बोलचाल की भाषा में समान्तर माध्य को औसत कहते हैं। समान्तर माध्य केन्द्रीय प्रवृत्ति का एक मापक है। वह संख्या जो किसी समूह विशेष के सभी आँकड़ों का प्रतिनिधित्व करती है, समान्तर माध्य कहलाती है। समान्तर माध्य वह मान है जो दिये हुए पदों के योगफल में पदों की संख्या से भाग देने पर प्राप्त होता है। उदाहरण के लिए-यदि छ: बालकों की आयु क्रमशः 5, 7, 9, 11, 13 व 15वर्ष है तो इसका समान्तर माध्य = [latex]\frac { 5+7+9+11+13+15 }{ 6 }[/latex] = [latex]\frac { 60 }{ 6 }[/latex] = 10 वर्ष होगा।

समान्तर माध्य निम्नलिखित रूप में परिभाषित किया जा सकता है
प्रो० होरेस सैक्रिस्ट के अनुसार, “एक समंकमाला के पदों के मूल्यों के योग को उनकी संख्या से भाग देने पर जो संख्या प्राप्त होती है, उसे ‘माध्य’ कहते हैं।”
क्रॉक्सटन व क्राउड़न के अनुसार, “माध्य समंकों के विस्तार के अन्तर्गत स्थित एक ऐसा मूल्य है जिसका प्रयोग श्रेणी के सभी मूल्यों का प्रतिनिधित्व करने के लिए किया जाता है, क्योंकि माध्य समंकों के विस्तार के अन्तर्गत ही कहीं होता है; अत: यह केन्द्रीय मूल्य का माप कहा जाता है।”

गणितीय माध्य या समान्तर माध्य के प्रकार
गणितीय या समान्तर माध्य के निम्नलिखित दो प्रकार होते हैं
1. सरल समान्तर माध्य तथा
2. भारित समान्तर माध्य।

1. सरले समान्तर माध्य – सरल समान्तर माध्य में समूह के सभी पदों या समंकों को समान महत्त्व दिया जाता है तथा इसकी गणना पदों के योगफल में पदों की संख्या से भाग देकर की जाती है।
2. भारित समान्तर माध्य – भारित समान्तर माध्य में प्रत्येक पद को उसके महत्त्व के अनुसार कम या अधिक भार प्रदान किया जाता है। पद मूल्यों को उसके महत्त्व के अनुसार भार देकर समान्तर माध्य निकालना ही भारित समान्तर माध्य कहलाता है।

प्रश्न 2
समान्तर माध्य के गुण-दोष लिखिए। [2008, 11, 12, 13, 15]
उत्तर:
समान्तर माध्य के गुण- समान्तर माध्य में निम्नलिखित गुण पाये जाते हैं

1. सरलता – समान्तर मध्य में सरलता का गुण पाया जाता है। एक साधारण व्यक्ति भी इसकी गणना सरलतापूर्वक कर सकता है, क्योंकि इसको समझना आसान होता है।
2. समस्त पदों का प्रतिनिधित्व – समान्तर माध्य ज्ञात करने के लिए सम्पूर्ण समंकों का प्रयोग किया जाता है; अत: यह सभी पदों का प्रतिनिधित्व करता है।
3. निश्चितता – संमान्तर मध्य सदैव एक ही होता है। श्रेणी चाहे जिस ढंग से लिखी जाए, इसमें कोई अन्तर नहीं आता; अत: इसमें निश्चितता का गुण पाया जाता है।
4. तुलना का आधार – समान्तर माध्य के द्वारा विभिन्न समंकों में तुलना की जा सकती है; अतः समान्तर माध्य तुलना का आधार प्रस्तुत करता है।
5. बीजगणितीय विवेचन सम्भव होता है – समान्तर माध्य का प्रयोग बीजगणितीय क्रियाओं में सम्भव है; अत: इस माध्य का प्रयोग उच्च-स्तरीय सांख्यिकीय विश्लेषण में किया जाता है।

समान्तर माध्य के दोष – समान्तर माध्य में निम्नलिखित दोष पाये जाते हैं

1. समान्तर माध्य ज्ञात करते समय सभी पदों को महत्त्व दिया जाता है, परन्तु बड़े मूल्यों के पद माध्य को अधिक प्रभावित करते हैं, जिसके कारण समान्तर माध्य श्रेणी का ठीक प्रतिनिधित्व करने में असफल रहता है; जैसे – किसी कार्यालय के प्रबन्धक का वेतन ₹14,000 और दो लिपिकों का वेतन क्रमशः ₹3,000 और ₹4,000 है तो इस समूह के वेतन का माध्य हैं ₹7,000 होगा, जो कि श्रेणी का उचित प्रतिनिधित्व नहीं करता।
2. समान्तर माध्य द्वारा कभी-कभी अशुद्ध परिणाम भी निकल जाते हैं। उदाहरण के लिए-यदि तीन फर्मों के विभिन्न वर्षों के लाभ निम्नवत् हैं
   
   उपर्युक्त लाभ को देखने से स्पष्ट होता है कि तीनों फर्मों का औसत लाभ या समान्तर माध्य 50,000 है। इस आधार पर यह निष्कर्ष निकाला जा सकता है कि तीनों फर्म समान प्रगति पर हैं, परन्तु फर्म A प्रगति पथ पर है और फर्म B की स्थिति शोचनीय।
3. गुणात्मक सामग्री का समान्तर माध्य ज्ञात नहीं किया जा सकता है। इस कारण गुणात्मक सामग्री के लिए यह अनुपयुक्त है।
4. समान्तर माध्य के द्वारा कभी-कभी विचित्र व हास्यास्पद परिणाम प्राप्त होते हैं; जैसे-एक व्यक्ति के पास 4 गाय हैं और दूसरे व्यक्ति के पास 3 गाय हैं तो इनका समान्तर माध्य 3.5 होता है। जबकि 3.5 गाय नहीं होती हैं; अत: जिन वस्तुओं का विभाजन असम्भव है उनके समान्तर माध्य को ज्ञात करना कठिन है।
5. समान्तर माध्य का बिन्दुरेखीय प्रदर्शन या रेखाचित्र असम्भव है।
6. समंकमाला को देखकर समान्तर मध्य का अनुमान लगाना कठिन होता है।
7. सम्पूर्ण समंकों में से यदि कोई एक समंक गायब हो जाता है, तो ऐसी स्थिति में समान्तर माध्य ज्ञात करना कठिन होता है।
8. समान्तर माध्य छोटे पदों को कम और बड़े पदों को अधिक महत्त्व देता है।

प्रश्न 3
समान्तर माध्य की गणना हेतु प्रयुक्त प्रत्यक्ष एवं लघु रीतियों को उदाहरण सहित समझाइए। [2010]
उत्तर:
समान्तर माध्य ज्ञात करने की दो विधियाँ हैं- 1. प्रत्यक्ष विधि (Direct Method) तथा 2. परोक्ष विधि या लघु विधि (Indirect or Short-cut Method)

1. प्रत्यक्ष विधि – समान्तर माध्य ज्ञात करने की यह विधि अत्यन्त सरल है, परन्तु यदि समंकों का मूल्य बड़ा होता है और उनकी संख्या भी अधिक होती है तो इस विधि का प्रयोग उचित नहीं रहता, क्योंकि गणना करने में अधिक समय व श्रम का व्यय होता है।

2. परोक्ष विधि या लघु विधि – इस विधि को अप्रत्यक्ष विधि या कल्पित माध्य विधि भी कहते हैं। इसमें दिये हुए पद-मूल्यों में से किसी एक को अथवा पद-मूल्यों से भिन्न किसी दूसरी संख्या को कल्पित माध्य (Assumed Mean) मान लेते हैं तथा कल्पित माध्य को प्रत्येक पद-मूल्य में से घटाकर धनात्मक या ऋणात्मक विचलन ज्ञात कर लेते हैं। कल्पित माध्य से प्रत्येक पद-मूल्य के विचलनों के योग को पदों की संख्या से भाग देते हैं। इस प्रकार जो भागफल प्राप्त होता है यदि वह धनात्मक (+) धनात्मक या ऋणात्मक विचलन ज्ञात कर लेते हैं। कल्पित माध्य से प्रत्येक पद-मूल्य के विचलनों के योग को पदों की संख्या से भाग देते हैं। इस प्रकार जो भागफल प्राप्त होता है यदि वह धनात्मक (+) होता है तो उसे कल्पित माध्य में जोड़ देते हैं और यदि ऋणात्मक (-) होता है तो उसे कल्पित माध्य से घटा देते हैं। जो मूल्य प्राप्त होता है वही समान्तर माध्य होता है। यदि समंकों का मूल्य बड़ा हो तथा समंकों की संख्या भी अधिक हो तो इस विधि का प्रयोग उचित होता है, क्योंकि गणना करने में समय व श्रम का कम व्यय होता है।

विशेष – समंक तीन प्रकार की श्रेणियों में मिल सकते हैं

1. व्यक्तिगत श्रेणी (Individual Series) में,
2. खण्डित श्रेणी (Discrete Series) में तथा
3. सतत् (अखण्डित) श्रेणी (Continuous Series) में। प्रत्येक प्रकार की श्रेणी का समान्तर मध्य प्रत्यक्ष या परोक्ष दोनों ही विधियों से ज्ञात किया जा सकता है।

व्यक्तिगत श्रेणी में समान्तर माध्य की गणना

(अ) प्रत्यक्ष विधि – व्यक्तिगत श्रेणी में सभी पदों के मूल्यों को जोड़कर, कुल योग को पदों की संख्या से भाग देते हैं।
सूत्र रूप में:

यहाँ, [latex]\overline { X }[/latex] संकेताक्षर का प्रयोग सरल समान्तर माध्य के लिए है। x¹, x², x³, x⁴, आदि व्यक्तिगत पद-मूल्य हैं तथा n पदों की संख्या है।
Σ(Sigma) ग्रीक भाषा का अक्षर है, जिसका अर्थ दिये गये समस्त पद-मूल्यों का योग है।

(ब) अप्रत्यक्ष विधि या लघु रीति – अप्रत्यक्ष विधि को कल्पित माध्य रीति भी कहते हैं। इसमें दिये हुए पद-मूल्यों में से किसी एक को अथवा पद-मूल्यों में से भिन्न किसी दूसरी संख्या को कल्पित माध्य मान लेते हैं, फिर निम्नलिखित क्रियाएँ करनी पड़ती हैं
सूत्र [latex]\overline { X }[/latex] = A + [latex]\frac { \Sigma dx }{ n } [/latex]
यहाँ
n A = offrea FTET (Assumed Mean)
Σdx = कल्पित माध्य से विचलन (Deviations from Assumed Mean)
n = पदों की संख्या

उदाहरण 1
एक कक्षा के 12 विद्यार्थियों के भार सम्बन्धी ऑकड़े निम्नलिखित हैं। प्रत्यक्ष तथा अप्रत्यक्ष रीति से समान्तर माध्य की गणना कीजिए
भार (किग्रा में) : 45         42       47        55      58        60          61       44      49         52         48        45
हल:
समान्तर माध्य की गणना (प्रत्यक्ष विधि से)

हल:
समान्तर माध्य की गणना (अप्रत्यक्ष विधि से)

खण्डित श्रेणी में समान्तर साध्य की गणना
खण्डित श्रेणी में प्रत्येक पद-मूल्य की तत्सम्बन्धी आवृत्तियाँ दी हुई रहती हैं। इस श्रेणी में भी समान्तर माध्य दोनों विधियों से ज्ञात किया जा सकता है।

(अ) प्रत्यक्ष विधि द्वारा – खण्डित श्रेणी में प्रत्यक्ष रीति से समान्तर माध्य ज्ञात करने के लिए पद-मूल्यों को सम्बन्धित आवृत्तियों से गुणा करके गुणनफलों के योग में कुल आवृत्तियों का भाग दे देते हैं।
सूत्र [latex]\overline { X }[/latex] = A + [latex]\frac { \Sigma fx }{ n } [/latex]
इस सूत्र में- fx = आवृत्ति का उसके मूल्य का गुणनफल।
Σfx = सभी गुणनफलों का योग।
n = आवृत्तियों का योग अर्थात् Σf

(ब) अप्रत्यक्ष (लघु) विधि – कल्पित माध्य से पद-मूल्यों का विचलन निकालकर सम्बन्धित आवृत्तियों से गुणा करते हैं। गुणनफलों के योग में कुल आवृत्तियों का भाग देने पर प्राप्त भागफल यदि धनात्मक है तो उसे कल्पित माध्य में जोड़ देते हैं और यदि ऋणात्मक है तो उसे कल्पित माध्य से घटा देते हैं। इस प्रकार समान्तर माध्य ज्ञात हो जाता है।
सूत्र [latex]\overline { X }[/latex] = A + [latex]\frac { \Sigma fdx }{ n } [/latex]
यहाँ A = कल्पित माध्य;
Σfdx = कल्पित माध्य से पद-मूल्यों के विचलनों व आवृत्तियों के गुणनफल का योग;
n = पदों की संख्या।

उदाहरण 2
निम्नांकित श्रेणी के समान्तर माध्य की गणना प्रत्यक्ष तथा अप्रत्यक्ष रीति से कीजिए

हल:
प्रत्यक्ष रीति से समान्तर माध्य की गणना

अप्रत्यक्ष रीति से समान्तर माध्य की गणना

सतत या अखण्डित श्रेणी में समान्तर माध्य की गणना
सतत् श्रेणी में मूल्य (x) वर्गों में दिये हुए रहते हैं; अतः सर्वप्रथम प्रत्येक वर्गान्तर का मध्य बिन्दु (mid point) या मध्य मूल्य (mid value) ज्ञात करते हैं। यह मध्य मूल्य M.V. को x यानि पद-मूल्य मानकर आगे की गणना की जाती है। इस प्रकार सतत् श्रेणी खण्डित श्रेणी में परिवर्तित हो जाती है। इसके बाद वे सभी क्रियाएँ करनी पड़ती हैं जो खण्डित श्रेणी में की जाती हैं। सतत् श्रेणी में समान्तर माध्य ‘प्रत्यक्ष विधि तथा ‘लघु विधि’ दोनों प्रकार से ज्ञात किया जा सकता है।

(अ) प्रत्यक्ष विधि – सतत् श्रेणी में प्रत्यक्ष रीति से समान्तर माध्य ज्ञात करने के लिए वर्गों के ‘मध्य मूल्य निकाले जाते हैं। तत्पश्चात् उनको आवृत्तियों (f) से गुणा करते हैं। गुणनफल के योग में
आवृत्तियों के योग से भाग दे देते हैं।
सूत्र [latex]\overline { X }[/latex] = A + [latex]\frac { \Sigma fx }{ n } [/latex]
इस सूत्र में – fx = आवृत्ति का सम्बन्धित मध्य मूल्य से गुणनफल।
Σfx = सभी गुणनफलों का योग।
n = आवृत्तियों का योग अर्थात् Σf ।

(ब) अप्रत्यक्ष या लघु विधि – सतत् श्रेणी में लघु विधि द्वारा समान्तर माध्य ज्ञात करना प्रत्यक्ष विधि की अपेक्षा सरल होता है। लघु विधि में समान्तर माध्य ज्ञात करने के लिए निम्नलिखित क्रियाएँ करनी पड़ती हैं

1. सर्वप्रथम वर्गान्तरों के मध्य मूल्य ज्ञात करते हैं।
2. मध्य मूल्य में से एक मूल्य या कोई अन्य कल्पित माध्य (A) मान लिया जाता है।
3. कल्पित माध्य को प्रत्येक मूल्य में से घटाकर विचलन (dx) ज्ञात करते हैं।
4. dx को तत्सम्बन्धी आवृत्तियों से गुणा कर fdx ज्ञात करते हैं।
5. गुणनफलों का योग करके Σfdx ज्ञात करते हैं।
6. समान्तर माध्य ज्ञात करने के लिए निम्नलिखित सूत्र का प्रयोग करते हैं

सूत्र- [latex]\overline { X }[/latex] = A + [latex]\frac { \Sigma fdx }{ n } [/latex]
यहाँ, A = कल्पित माध्य;
fdx = कल्पित माध्य से विचलन X आवृत्ति;
Σfdx = आवृत्ति तथा विचलन के गुणनफल का योग;
n = पदों की संख्या।

उदाहरण 3
निम्नलिखित तालिका में दिये गये आँकड़ों के आधार पर समान्तर माध्य की गणना प्रत्यक्ष तथा अप्रत्यक्ष रीति से कीजिए विद्यार्थियों की संख्या

हल:
प्रत्यक्ष विधि द्वारा समान्तर माध्य की गणना

अप्रत्यक्ष विधि द्वारा समान्तर माध्य की गणना

संचयी आवृत्तियाँ दिये रहने पर समान्तर माध्य की गणना
सतत् श्रेणी में संचयी आवृत्तियाँ दो प्रकार से हो सकती हैं
(1) ‘से अधिक’ तथा (2) ‘से कम। दोनों प्रकार से दी गयी संचयी आवृत्तियों में समान्तर माध्य की गणना उदाहरण 4 तथा 5 द्वारा स्पष्ट की जा रही है।

उदाहरण 4
निम्नलिखित आवृत्ति वितरण से समान्तर माध्य ज्ञात कीजिए

हल:
उपर्युक्त प्रश्न ‘से अधिक के आधार पर संचयी आवृत्ति में दिया हुआ है। इसमें वर्गों की निम्न सीमाएँ दी गयी हैं; अत: इसे सर्वप्रथम सतत् श्रेणी में बदलेंगे। श्रेणी को देखने से ज्ञात होता है कि श्रेणी में वर्गान्तर 10 का है। अत: पहला वर्ग 10-20 का बनेगा तथा पहले संचयी आवृत्ति में से अगली संचयी आवृत्ति को घटाते जाएँगे, अर्थात् संचयी आवृत्ति से सामान्य आवृत्ति बनाएँगे; अब साधारण श्रेणी में प्रश्न निम्नलिखित प्रकार से बनेगा

हल:

उदाहरण 5
निम्नलिखित आवृत्ति-वितरण से समान्तर माध्य ज्ञात कीजिए

हल:
उपर्युक्त प्रश्न ‘से कम के आधार पर संचयी आवृत्ति में दिया हुआ है। इसमें वर्गान्तर की उच्च सीमाएँ दी हैं। हम देखते हैं कि श्रेणी के प्रत्येक वर्ग में अन्तर 10 का है। सर्वप्रथम हम इसे सतत् श्रेणी में बदलेंगे। हमारा पहला वर्ग 10-20 का होगा। प्रत्येक वर्ग की आवृत्ति ज्ञात करने के लिए अगले वर्ग की संचयी आवृत्ति में से पहले वर्ग की संचयी आवृत्ति घटा देंगे। सतत् श्रेणी में प्रश्न निम्नलिखित प्रकार से बनेगा

हल:

उदाहरण 6
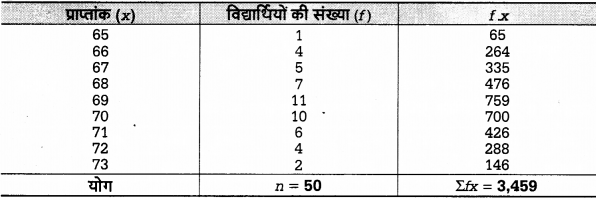
निम्नलिखित श्रेणी से समान्तर माध्य ज्ञात कीजिए

हल:
विशेष – समानान्तर माध्य ज्ञात करने की दोनों विधियाँ (प्रत्यक्ष एवं अप्रत्यक्ष) इस प्रश्न के हल हेतु दर्शायी गयी हैं

विशेष – समान्तर माध्य ज्ञात करने की यह कोई भिन्न विधि नहीं है, वरन् लघु विधि की सहायक विधि ही है। इस विधि में कल्पित माध्य से अन्तर की संख्याओं को किसी उभयनिष्ठ संख्या से भाग दे दिया जाता है, जिससे पद-विचलन बहुत छोटे हो जाते हैं। इस प्रकार इन छोटे पद-विचलनों में उनकी आवृत्तियों से गुणा करने पर कुल विचलन ज्ञात हो जाते हैं। अन्त में विचलनों के योग में उक्त उभयनिष्ठ संख्या का गुणा कर दिया जाता है। शेष विधि वही रहती है जिसे लघु विधि के अन्तर्गत समझाया गया है। चिह्नों के अर्थ भी वही होते हैं जिन्हें लघु रीति के अन्तर्गत स्पष्ट किया गया है।

उदाहरण 7
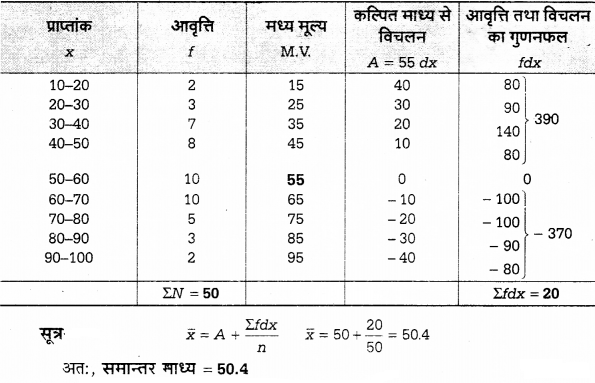
एक परीक्षा में 50 विद्यार्थियों द्वारा प्राप्तांक नीचे तालिका में दिये गये हैं। अंकगणितीय माध्य की गणना कीजिए

हल:

उदाहरण 8

या
निम्न समंकों में से समान्तर माध्य ज्ञात कीजिए [2014]

या
निम्नलिखित श्रेणी के समान्तर माध्य की गणना कीजिए [2014]

या
निम्नलिखित आवृत्ति वितरण में समान्तर माध्य ज्ञात कीजिए [2014]

हल:

प्रश्न 4
भारित समान्तर माध्य क्या है? भारित समान्तर माध्य ज्ञात करने की विधि उदाहरण के द्वारा समझाइए।
उत्तर:
आर्थिक समस्याओं के अध्ययन में भारित समान्तर माध्य का महत्त्वपूर्ण स्थान होता है। यह वह माध्य होता है जिसमें पदों को उनके सापेक्षिक महत्त्व के अनुसार भार देकर माध्य की गणना की जाती है। अनेक स्थितियों में तुलना करने के लिए भारित समान्तर माध्य ही उपयुक्त विधि होती है। उदाहरणार्थ-एक कारखाने के कर्मचारियों की औसत आय ज्ञात करने के लिए व्यवस्थापक के वेतन तथा कर्मचारियों के वेतन को समान महत्त्व देना अनुचित होगा; क्योंकि कारखाने में व्यवस्थापक तो एक होगा तथा कर्मचारियों की संख्या अधिक होगी। उचित औसत आय तब ही प्राप्त हो सकती है, जब हम व्यवस्थापक तथा कर्मचारियों को उनके महत्त्व के अनुसार भार दें। इसके लिए भारित समान्तर माध्य ही उपयुक्त है।

भारित समान्तर माध्य ज्ञात करने की विधियाँ – भारित समान्तर माध्य भी प्रत्यक्ष विधि एवं अप्रत्यक्ष या लघु विधि से ज्ञात किया जा सकता है

(क) प्रत्यक्ष विधि से भारित समान्तर माध्य – (1) प्रत्येक पद को उसके महत्त्व के आधार पर भार (w) प्रदान किया जाता है।
(2) प्रत्येक मूल्य (x) को उसके भार (W) से गुणा करके गुणनफल (Wx) ज्ञात करते हैं। इसके बाद गुणनफलों का योग करके ΣWx निकालते हैं। ।
(3) गुणनफलों (Σwx) में भारों के योग (ΣW) का भाग देकर समान्तर माध्य निकालते हैं। सूत्र रूप में
[latex]\overline { X }[/latex] = A + [latex]\frac { \Sigma Wx }{ \Sigma W } [/latex]
यहाँ, [latex]\overline { X }[/latex] w = भारित समान्तर माध्य है।
ΣWx = मूल्यों तथा भारों के गुणनफलों का योग है।
Σw = भारों का योग है।

(ख) लघु रीति से भारित समान्तर माध्य – इस विधि द्वारा भारित समान्तर माध्य ज्ञात करने के लिए निम्नलिखित क्रियाएँ करनी पड़ती हैं

1. प्रत्येक पद को महत्त्व के अनुसार भार देना।
2. कल्पित माध्य (A) मानकर मूल्यों से विचलन (dx) ज्ञात करना।
3. विचलनों को तत्सम्बन्धी भार से गुणा करके गुणनफल ज्ञात करना तथा उनका योग करना। इस प्रकार ΣWdx ज्ञात हो जाएगा।
4. निम्नलिखित सूत्र का प्रयोग करके भारित समान्तर माध्य ज्ञात किया जाएगा

[latex]\overline { X }[/latex]W = A + [latex]\frac { \Sigma Wdx }{ \Sigma W } [/latex]
यहाँ परे, [latex]\overline { X }[/latex]W = भारित समान्तर माध्य;
A = कल्पित माध्य।
ΣWdx = कल्पित माध्य से प्राप्त विचलनों और तत्सम्बन्धी भारों के गुणनफल का योग।
Σw = भारों का योग।

उदाहरण 9
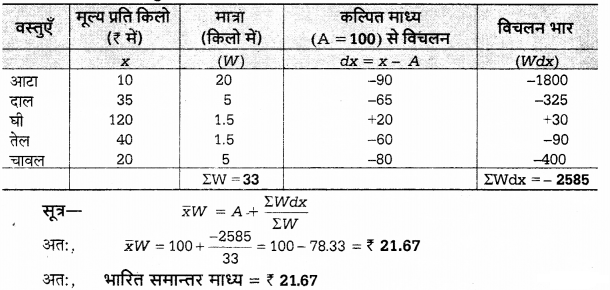
एक व्यक्ति ने निम्नलिखित वस्तुएँ विविध मूल्यों पर नीचे दी गयी तालिका के अनुसार खरीदी हैं। उनका भारित समान्तर माध्य ज्ञात कीजिए

हल:
प्रत्यक्ष विधि द्वारा भारित समान्तर माध्य की गणना।


लघु रीति द्वारा भारित समान्तर माध्य की गणना

लघु उत्तरीय प्रश्न (4 अंक)

प्रश्न 1
निम्नांकित समंकों की सहायता से प्राप्तांकों का समान्तर माध्य ज्ञात कीजिए। प्रश्न-पत्र के अधिकतम अंक 50 थे

हल:
[ संकेत–उपर्युक्त प्रश्न व्यक्तिगत श्रेणी के अन्तर्गत आता है। ] ।
समान्तर माध्य सूत्र

प्रश्न 2
निम्नलिखित आँकड़ों से लघु विधि द्वारा समान्तर माध्य ज्ञात कीजिए
7, 10, 13, 18, 24, 30
हल:

प्रश्न 3
उत्तर प्रदेश सरकार के निम्नलिखित वार्षिक व्यय के माध्य की गणना कीजिए

हल:
समान्तर माध्य की गणना

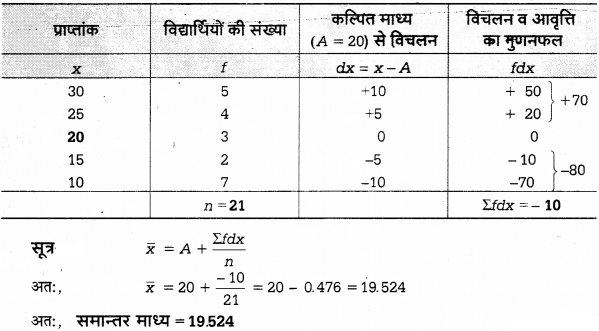
प्रश्न 4
लघु विधि द्वारा समान्तर माध्य ज्ञात कीजिए गणना

हल:
लघु विधि द्वारा समान्तर माध्य

प्रश्न 5
8 व्यक्तियों के समूह के मासिक व्यय का समान्तर माध्य ₹5,000 है। 12 व्यक्तियों के एक समूह का समान्तर माध्य ₹6,000 है। सभी 20 व्यक्तियों के मासिक व्यय का समान्तर माध्य ज्ञात करें।
हल:
समान्तर माध्य की गणना

प्रश्न 6
एक शहर के 100 परिवारों की मासिक आय निम्नवत है

उपर्युक्त आँकड़ों की सहायता से इस शहर के परिवारों की मासिक आय का समान्तर माध्य लघु विधि द्वारा ज्ञात कीजिए।
हल:
विधि द्वारा समान्तर माध्य की गणना

प्रश्न 7
निम्नांकित श्रेणी से समान्तर माध्य की गणना प्रत्यक्ष तथा लघु दोनों रीति से कीजिए

हल:
प्रत्यक्ष एवं लघु विधि द्वारा समान्तर माध्य की गणना

प्रश्न 8
निम्नलिखित का प्रत्यक्ष और अप्रत्यक्ष विधियों द्वारा समान्तर माध्य ज्ञात कीजिए

हल:
संकेत – सर्वप्रथम वर्गान्तर समान अन्तराल के बनाने होंगे; क्योकि पहले वर्गान्तर में 1 का अन्तर है, दूसरे व तीसरे में 2 का तथा चौथे व पाँचवें में 5 का। अतः सुविधा के लिए पहले, दूसरे व तीसरे को मिलाकर एक वर्गान्तर बना लेंगे, जिसमें 5 का अन्तर होगा।

प्रत्यक्ष तथा अप्रत्यक्ष विधि द्वारा समान्तर माध्य की गणना

प्रश्न 9
निम्नांकित का लघु विधि द्वारा समान्तर माध्य ज्ञात कीजिए

हल:
लघु विधि द्वारा समान्तर माध्य की गणना

प्रश्न 10
क, ख और ग आगरा के किसी इण्टरमीडिएट कॉलेज के परीक्षार्थी हैं। इन्होंने निम्नलिखित प्रश्न का समान्तर माध्य निकाला। तीनों परीक्षार्थियों के उत्तर एक-दूसरे से भिन्न थे। क का उत्तर 347, जबकि ख और ग के उत्तर क्रमशः 35 और 37 थे। समान्तर माध्य की गणना करके ज्ञात कीजिए कि इन परीक्षार्थियों में किसका उत्तर सही है?

हल:

प्रश्न 11
एक विद्यार्थी के पाँच विषयों में प्राप्त अंकों का समान्तर माध्य 40 है। छठे विषय में प्राप्त अंकों को सम्मिलित कर लेने पर समान्तर माध्य 46 हो जाता है। छठे विषय में उसे कितने अंक मिले?
हल:
पाँच विषयों में प्राप्त अंकों का समान्तर माध्य = 40
पाँच विषयों में कुल प्राप्त अंक = 40 x 5 = 200
छः विषयों में प्राप्त अंकों का समान्तर माध्य = 46
छः विषयों में कुल प्राप्त अंक। = 46 x 6 = 276
छठे विषय में प्राप्तांक = छः विषयों के कुल प्राप्तांक-पाँच विषयों के कुल प्राप्तांक
छठे विषय के प्राप्तांक = 276 – 200 = 76

प्रश्न 12
निम्नलिखित आँकड़ों से लघु विधि द्वारा समान्तर माध्य ज्ञात कीजिए

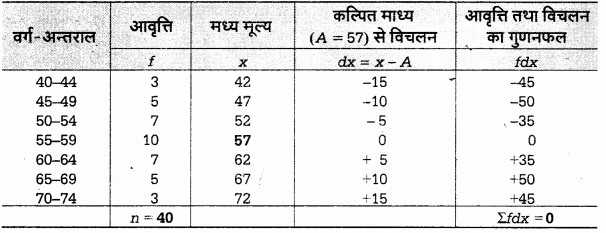
हल:
लघु विधि द्वारा समान्तर माध्य की गणना

प्रश्न 13
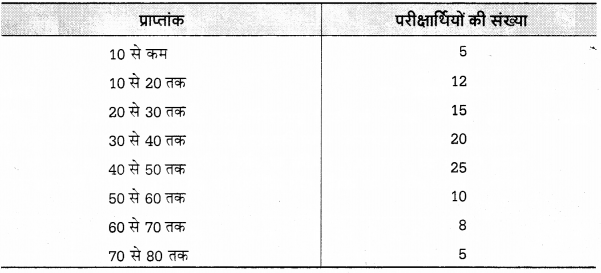
निम्नलिखित आँकड़ों से प्राप्तांकों का समान्तर माध्य ज्ञात कीजिए

हल:
सर्वप्रथम वर्गान्तर को अपवर्जी श्रेणी बनाकर तथा संचयी आवृत्ति को सामान्य आवृत्ति में बदल लेंगे, तत्पश्चात् प्रश्न को अग्रवत् हल करेंगे

प्रश्न 14
10 छात्रों के अंक इस प्रकार हैं
10, 28, 32, 12, 18, 20, 25, 15, 26, 14. प्रत्यक्ष विधि से समान्तर माध्य ज्ञात कीजिए।
हल:

प्रश्न 15
निम्नलिखित समंकों में से प्रत्यक्ष रीति द्वारा समान्तर माध्य ज्ञात कीजिए

हल:

प्रश्न 16
निम्नलिखित समंकों में से अप्रत्यक्ष विधि से समान्तर माध्य ज्ञात कीजिए

हल:
समान्तर माध्य की गणना

अतिलघु उत्तरीय प्रश्न (2 अंक)

प्रश्न 1
समान्तर माध्य की गणना हेतु व्यक्तिगत श्रेणी की प्रत्यक्ष विधि का सूत्र लिखिए।
उत्तर:

प्रश्न 2
एक आदर्श माध्य के गुण बताइए।
उत्तर:
एक आदर्श माध्य में निम्नलिखित आवश्यक गुण होने चाहिए

1. स्पष्ट परिभाषा।
2. श्रेणी के सभी पदों पर आधारित।
3. माध्य सरल होना चाहिए।
4. अंकगणितीय एवं बीजगणितीय विवेचन सम्भव।
5. उच्चावचनों का कम प्रभाव।
6. माध्य से निकाली गयी संख्या निश्चित एवं निरपेक्ष होनी चाहिए।

प्रश्न 3
एक व्यक्ति की मासिक आय रुपये में नीचे दी गयी है। प्रत्यक्ष विधि से समान्तर माध्य कीजिए [2008]
1400, 1350, 1500, 1750, 1100
हल:

प्रश्न 4
निम्नलिखित आवृत्ति सारणी के आधार पर छात्रों को प्राप्त अंकों का समान्तर माध्य ज्ञात कीजिए [2007]

हल:

निश्चित उतरीय प्रश्न (1 अंक)

प्रश्न 1
समान्तर माध्य किसे कहते हैं? [2008, 11, 12, 13, 15]
या
समान्तर माध्य को परिभाषित कीजिए। [2013, 14]
उत्तर:
समान्तर माध्य वह मान है जो दिये हुए पदों के योगफल में पदों की संख्या से भाग देने पर प्राप्त होता है।
या
वह संख्या जो किसी समूह विशेष के सभी आँकड़ों का प्रतिनिधित्व करती है, उस समूह का समान्तर माध्य कहलाती है।

प्रश्न 2
समान्तर माध्य कितने प्रकार के होते हैं?
उत्तर:
समान्तर माध्य दो प्रकार के होते हैं

1. सरल समान्तर माध्य तथा
2. भारित समान्तर माध्य।

प्रश्न 3
सरल समान्तर माध्य से क्या अभिप्राय होता है?
उत्तर:
सरल समान्तर माध्य की गणना पदों के योगफल में पदों की संख्या से भाग देकर की जाती है। सरल समान्तर माध्य में समूह के सभी पदों या समंकों को समान महत्त्व दिया जाता है।

प्रश्न 4
भारित समान्तर माध्य से क्या अभिप्राय होता है? [2009, 11]
उत्तर:
भारित समान्तर माध्य में प्रत्येक पद को उसके महत्त्व के अनुसार कम या अधिक भार प्रदान किया जाता है।
पद मूल्यों को उसके महत्त्व के अनुसार भार देकर समान्तर माध्य ज्ञात करना भारित समान्तर माध्य है।

प्रश्न 5
समान्तर माध्य की तीन सीमाओं की व्याख्या कीजिए।
उत्तर:
(1) समान्तर माध्य की गणना करते समय सभी समंक समान गुण वाले होने चाहिए।
(2) उच्चावचनों का कम प्रभाव होना चाहिए।
(3) समान्तर माध्य की गणना योग्य एवं कुशल व्यक्ति के द्वारा की जानी चाहिए जिससे कि समान्तर माध्य शुद्ध प्राप्त हो सके।

प्रश्न 6
अप्रत्यक्ष विधि से समान्तर माध्य ज्ञात करने का सूत्र लिखिए।
उत्तर:

प्रश्न 7
समान्तर माध्य के दो गुण बताइए।
उत्तर:
(1) समान्तर माध्य में सरलता का गुण पाया जाता है।
(2) समान्तर माध्य सभी पदों का प्रतिनिधित्व करता है।

प्रश्न 8
समान्तर माध्य के दो दोष लिखिए।
उत्तर:
(1) समान्तर माध्य ज्ञात करने में सभी पदों को महत्त्व दिया जाता है। किन्तु बड़े मूल्यों के पद समान्तर माध्य को अधिक प्रभावित करते हैं।
(2) समान्तर माध्य द्वारा कभी-कभी अशुद्ध परिणाम भी निकल जाते हैं।

प्रश्न 9
समान्तर माध्य की गणना हेतु व्यक्तिगत श्रेणी की प्रत्यक्ष विधि का सूत्र लिखिए।
उत्तर:

प्रश्न 10
समान्तर माध्य की गणना हेतु व्यक्तिगत श्रेणी की अप्रत्यक्ष विधि का सूत्र लिखिए। [2009,11]
उत्तर:

प्रश्न 11
समान्तर माध्य की गणना हेतु खण्डित श्रेणी की प्रत्यक्ष विधि का सूत्र लिखिए। [2009, 11]
उत्तर:

प्रश्न 12
समान्तर माध्य की गणना हेतु खण्डित श्रेणी की अप्रत्यक्ष विधि का सूत्र लिखिए।
उत्तर:

प्रश्न 13
भारित समान्तर माध्य की गणना हेतु लघु विधि का सूत्र लिखिए।
उत्तर:
भारित समान्तर माध्य का लघु विधि का सूत्र

बहुविकल्पीय प्रश्न (1 अंक)

प्रश्न 1
केन्द्रीय प्रवृत्ति की एक माप है
(क) समान्तर माध्य
(ख) माध्य विचलन
(ग) प्रमाप विचलन
(घ) सह-सम्बन्ध
उत्तर:
(क) समान्तर माध्य।

प्रश्न 2
समान्तर माध्य का मूल्य श्रेणी के सभी चरों के मूल्य के
(क) योग के बराबर होता है।
(ख) वर्गों के योग के बराबर होता है।
(ग) योग में चरों की संख्या से गुणा करने पर प्राप्त मूल्य के बराबर होता है।
(घ) योग में चरों की संख्या से भाग देने पर प्राप्त मूल्य के बराबर होता है ।
उत्तर:
(घ) योग में चरों की संख्या से भाग देने पर प्राप्त मूल्य के बराबर होता है।

प्रश्न 3
खण्डित या विच्छिन्न श्रेणी में प्रत्यक्ष रीति से समान्तर माध्य निकालने का सूत्र है

उत्तर:

प्रश्न 4
खण्डित या विच्छिन्न श्रेणी में अप्रत्यक्ष रीति से समान्तर माध्य निकालने का सूत्र है

उत्तर:

प्रश्न 5
अविच्छिन्न अथवा सतत् श्रेणी में प्रत्यक्ष रीति से समान्तर माध्य निकालने का सूत्र है

उत्तर:

प्रश्न 6
अविच्छिन्न अथवा सतत् श्रेणी में अप्रत्यक्ष रीति से समान्तर माध्य निकालने का सूत्र है

उत्तर:

प्रश्न 7
53 छात्रों के प्राप्तांकों का समान्तर माध्य 53 है। यदि प्रत्येक छात्र के प्राप्तांकों में 3 की वृद्धि कर दी जाए तो प्राप्तांकों का समान्तर माध्य
(क) 53 +[latex]\frac { 3 }{ 53 }[/latex] = 53 [latex]\frac { 3 }{ 53 }[/latex] हो जाएगा।
(ख) 53 + 3 = 56 हो जाएगा।
(ग) 53 +[latex]\frac { 3 }{ 4 }[/latex] = 54[latex]\frac { 1 }{ 2 }[/latex] हो जाएगा।
(घ) 53 + 3² = 62 हो जाएगा।
उत्तर:
(ख) 53 +3 = 56 हो जाएगा।