UP Board Solutions for Class 12 Economics Chapter 28 Measure of Central Tendency: Median (केन्द्रीय प्रवृत्ति की माप : माध्यिका)

UP Board Solutions for Class 12 Economics Chapter 28 Measure of Central Tendency: Median (केन्द्रीय प्रवृत्ति की माप : माध्यिका)

UP Board Solutions for Class 12 Economics Chapter 28 Measure of Central Tendency: Median (केन्द्रीय प्रवृत्ति की माप : माध्यिका)

विस्तृत उत्तरीय प्रश्न (6 अंक)

प्रश्न 1
मध्यका से आप क्या समझते हैं ? इसको परिभाषित करते हुए इसकी विशेषताओं पर संक्षेप में प्रकाश डालिए। [2011]
उत्तर:
माध्यिका या मध्यका समंक श्रेणी का वह गतिशील मूल्य है जो समंकमाला को दो बराबर भागों में इस प्रकार विभाजित करता है कि एक भाग के सारे मूल्य मध्यका से अधिक तथा दूसरे भाग के सारे मूल्य मध्यका से कम होते हैं। यदि किसी समंकमाला को आरोही या अवरोही क्रम में व्यवस्थित किया जाए तो श्रेणी के बीच के मूल्य को माध्यिका कहते हैं।

मध्यका की कुछ प्रमुख परिभाषाएँ निम्नलिखित हैं
कॉनर के अनुसार, “मध्यका समंक श्रेणी का वह चर मूल्य है, जो क्रमबद्ध समंकमाला को दो बराबर भागों में इस प्रकार बाँटता है कि एक भाग में सारे मूल्य माध्यिका से अधिक और दूसरे भाग में सारे मुल्य उससे कम होते हैं।”
डॉ० बाउले के अनुसार, “यदि एक समूह के पदों को मूल्यों के आधार पर क्रमबद्ध किया जाए। तो लगभग मध्य पद का मूल्य ही मध्यको होगा।”

मध्यका की विशेषताएँ
मध्यका की प्रमुख विशेषताएँ निम्नलिखित हैं

1. मध्यका एक स्थिति सम्बन्धी माध्य है।
2. यह आरोही या अवरोही समंकमाला को दो बराबर भागों में बाँट देती है।
3. मध्यका के मूल्य पर अति सीमान्त इकाइयों का प्रभाव बहुत कम होता है।
4. यह समंकमाला का केन्द्रीय मूल्य होता है।
5. एक भाग के सभी मूल्य मध्यका से कम तथा दूसरे भाग के सभी मूल्य मध्यका से अधिक होते हैं।
6. अन्य माध्यों की तरह मध्यका का गणितीय विवेचन नहीं करना होता।

प्रश्न 2
माध्यिका के गुण-दोष लिखिए। [2011]
उत्तर:
माध्यिका के गुण
माध्यिका या मध्यका के गुण निम्नलिखित हैं

1. बुद्धिमत्ता, सुन्दरता आदि गुणात्मक विशेषताओं के अध्ययन के लिए अन्य माध्यों की अपेक्षा मध्यका श्रेष्ठ समझी जाती है।
2. मध्यका को बिन्दुरेखीय पद्धति से भी ज्ञात किया जा सकता है।
3. मध्यका की गणना हेतु श्रेणी के सभी मूल्यों का ज्ञान आवश्यक नहीं। केवल मदों की संख्या व मध्यका वर्ग का ज्ञान पर्याप्त है।
4. मध्यका सीमान्त पदों से प्रभावित नहीं होती।
5. मध्यको की गणना सरलता से की जा सकती है।
6. यदि आवृत्तियों की प्रवृत्ति श्रेणी के मध्य समान रूप से विपरीत होने की हो तो मध्यका एक विश्वसनीय माध्य माना जाता है।
7. मध्यको सदैव निश्चित एवं स्पष्ट होती है। सामान्य ज्ञान रखने वाले व्यक्ति के द्वारा भी इसे आसानी से ज्ञात किया जा सकता है।

माध्यिका के दोष माध्यिका या मध्यका के दोष निम्नलिखित हैं

1. जब पदों की संख्या सम होती है तो मध्यका का सही मूल्य ज्ञात करना सम्भव नहीं हो पाता। ऐसी स्थिति में मध्यका का मान केवल अनुमानित रूप में ही ज्ञात होता है।
2. मध्यका ज्ञात करते समय, यदि इकाइयों की संख्या में वृद्धि कर दी जाए तो इसका मूल्य बदल जाता है।
3. जिन स्थानों पर श्रेणी के सीमान्त पदों का भार देना हो उन स्थानों के लिए मध्यको उपयुक्त नहीं रहती।।
4. इसका प्रयोग बीजगणितीय क्रियाओं में नहीं किया जा सकता।
5. इसकी गणना के लिए यह आवश्यक है कि पहले श्रेणी को आरोही या अवरोही क्रम में व्यवस्थित किया जाए।
6. यदि मध्यका तथा पदों की संख्या दी गयी हो तो इनके गुणा करने पर मूल्यों का कुल योग प्राप्त नहीं किया जा सकता। समान्तर माध्य की तरह यह गुण मध्यका में नहीं होता।
7. यदि मूल्यों का वितरण अनियमित हो तो मध्यका प्रतिनिधि अंक प्रस्तुत नहीं करता; जैसे – एक विद्यार्थी को 5 विषयों में क्रमश: 20, 10, 3, 1, 0 अंक प्राप्त हुए हों। मध्यको अंक 3 होगा जो कि उचित प्रतीत नहीं होता।

प्रश्न 3
मध्यका या माध्यिका की गणना हेतु विभिन्न श्रेणियों में प्रयुक्त रीतियों को उदाहरण सहित समझाइए।
उत्तर:
विभिन्न प्रकार की श्रेणियों में मध्यका की गणना
(क) व्यक्तिगत श्रेणी में  – व्यक्तिगत श्रेणी में मध्यका निम्नलिखित विधि से ज्ञात की जाती है|
(1) सर्वप्रथम श्रेणी के सभी पदों को आरोही (Ascending) या अवरोही (Descending) क्रम में रखते हैं।
(2) पद, सम हो या विषम, मध्यका ज्ञात करने के लिए निम्नलिखित सूत्र का प्रयोग करते हैं
M = Value of [latex]\frac { N+1 }{ 2 }[/latex] th item
यहाँ पर, M = माध्यिका या मध्यका, N = पदों की संख्या।।

उदाहरण 1
निम्नलिखित समंकों से मध्यका ज्ञात कीजिए [2009]
18,   20,   25,   12,   15,   25,   28,   30,   10.
हल:
पदों को आरोही क्रम में व्यवस्थित करने परसंख्या

सूत्र – M = [latex]\frac { N+1 }{ 2 }[/latex] वें पद का मूल्य
अतः, M = [latex]\frac { 9+1 }{ 2 }[/latex] = [latex]\frac { 10 }{ 2 }[/latex] = 5वें पद का मूल्य
या, M = 5 वें पद का मूल्य = 20
अतः, मध्यका = 20
विशेष – व्यक्तिगत श्रेणी में यदि संख्या सम है तब [latex]\frac { N+1 }{ 2 }[/latex]th में मध्यका आकार पूर्णांक में नहीं होगा। ऐसी स्थिति में मध्यका की गणना निम्नलिखित उदाहरण में समझायी जा रही है

उदाहरण 2
निम्नलिखित समंकों की माध्यिका ज्ञात कीजिए
50,   10,   7,  5,   18,   22,   25,   36,   12.
हल:
पदों को आरोही क्रम में व्यवस्थित करने पर

(ख) खण्डित श्रेणी में – खण्डित श्रेणी में माध्यिका ज्ञात करने के लिए सर्वप्रथम बारम्बारता (आवृत्ति) को संचयी बारम्बारता में बदल देते हैं। इसके पश्चात् व्यक्तिगत श्रेणी में प्रयुक्त किये गये सूत्र [latex]\frac { N+1 }{ 2 }[/latex] द्वारा माध्यिका पद ज्ञात किया जाता है। वह पद जिस संचयी आवृत्ति में समाहित होता है, वही मध्यका होती है।

उदाहरण 3
कुछ परीक्षार्थियों के प्राप्तांक निम्नलिखित हैं। इनकी मध्यका ज्ञात कीजिए [2009, 10]

हल:
मध्यका की गणना

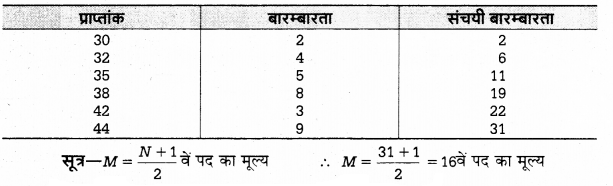
यहाँ 16 वाँ पद संचयी बारम्बारता 19 में निहित है और 19वें पद का मूल्य = 38
अतः, मध्यका = 38

विशेष – मध्यका का मूल्य निर्धारित करने के लिए [latex]\frac { N+1 }{ 2 }[/latex] वें पद के मूल्य को सदैव संचयी आवृत्ति के कॉलम में देखा जाता है तथा उस संचयी आवृत्ति के सम्मुख का पद मध्यको होता है। यह आवश्यक नहीं है कि वह पद संचयी आवृत्ति के कॉलम में मिल ही जाए, किन्तु वह पद संचयी आवृत्ति के जिस पद में निहित होता है उसी के सामने का पद मध्यका होता है।

(ग) सतत् श्रेणी – सतत् या अविच्छिन्न श्रेणी में मध्यका अग्रलिखित क्रमिक पद्धति की सहायता से ज्ञात की जाती है

1. सबसे पहले यदि दी गयी श्रेणी समावेशी (Inclusive) हो तो उसे अपवर्जी (Exclusive) श्रेणी में परिवर्तित करना चाहिए।
2. इसके बाद साधारण आवृत्तियों को संचयी आवृत्तियों में परिवर्तित करते हैं।
3. इसके बाद m = [latex]\frac { N}{ 2 }[/latex] की सहायता से मध्यका पद ज्ञात किया जाता है।
4. मध्यका पद जिस संचयी आवृत्ति में निहित होता है उसका मूल्य उसके सम्मुख के वर्ग–अन्तराल में निहित होता है। मध्यका-मूल्य इस वर्गान्तर की उच्च और निम्न सीमाओं के बीच ही होता है। इसे ज्ञात करने के लिए आन्तरगणन या अन्तर्वेशन (Interpolation) के निम्नलिखित सूत्र का प्रयोग करते हैं

सूत्र – M = L₁ + [latex]\frac { { L }_{ 2 }-{ L }_{ 1 } }{ f }[/latex] (m – c)
यहाँ पर, M = मध्यका,
L₁ = मध्यका वर्ग की निम्न सीमा, L₂ = मध्यका वर्ग की उच्च सीमा,
f = मध्यका वर्ग की बारम्बारती,
m = मध्य पद,
c = मध्यका वर्ग से पहले वाले वर्ग की संचयी बारम्बारता।

लघु उत्तरीय प्रश्न, (4 अंक)

उदाहरण 1
निम्नलिखित समंकों की सहायता से मध्यका ज्ञात कीजिए

या
निम्न समंकों की सहायता से माध्यिका ज्ञात कीजिए

या
निम्न समंकों में माध्यिका ज्ञात कीजिए [2014]

हल:

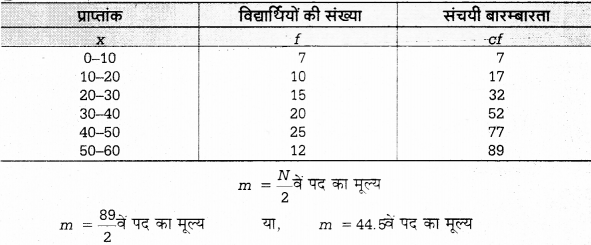
मध्यका का आकार 44.5वें पद का मूल्य 52 संचयी आवृत्ति में निहित है और यह संचयी आवृत्ति 30-40 वर्ग में स्थित है; अतः माध्यिका मूल्य इस वर्ग के अन्तर्गत ही स्थित होगा।

उदाहरण 2
निम्नांकित समंकों से मध्यका ज्ञात कीजिए [2009, 10]

हल:
सर्वप्रथम समावेशी श्रेणी को अपवर्जी श्रेणी में निम्नलिखित रूप में बदला जाना चाहिए

स्पष्ट है कि मध्यका का आकार 62.5 वें पद का मूल्य संचयी आवृत्ति 90 में आता है और यह संचयी आवृत्ति 20.5 – 25.5 वर्ग में स्थित है; अतः मध्यका मूल्य इस वर्ग के अन्तर्गत ही स्थित होगा।

उदाहरण 3
निम्नलिखित आवृत्ति वितरण का मध्यमान ज्ञात कीजिए।

हल:

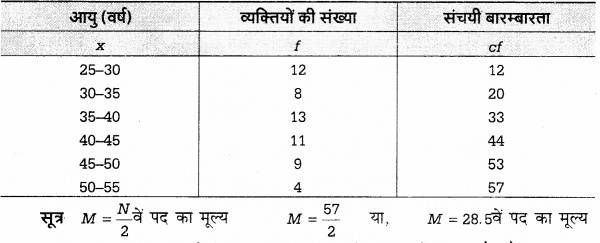
मध्यका का आकार 28.5वें पद का मूल्य 33 संचयी आवृत्ति में निहित है और यह संचयी आवृत्ति 35-40 वर्ग में स्थित है, अतः मध्यका मूल्य इस वर्ग के अन्तर्गत ही स्थित होगा।

अतिलघु उत्तरीय प्रश्न (2 अंक)

प्रश्न 1
9 छात्रों के अर्थशास्त्र विषय में अंक निम्नलिखित प्रकार से हैं
43,   47,   19,   26,   35,   36,   41,   29,   32.
इन अंकों से मध्यका ज्ञात कीजिए।
हल:
पदों को आरोही क्रम में लिखने पर व्यक्तिगत श्रेणी, संख्या

प्रश्न 2
माध्यमिक शिक्षा परिषद्, उत्तर प्रदेश की कक्षा 12 अर्थशास्त्र की परीक्षा में परीक्षार्थियों ने निम्नलिखित अंक प्राप्त किये

प्राप्तांकों की मध्यका ज्ञात कीजिए।
हल:
सर्वप्रथम पदों को आरोही क्रम में निम्नवत् व्यवस्थित कीजिए

23वें पद को मूल्य संचयी आवृत्ति 27 में है; अत: 27वें पद का मूल्य = 28
अतः, मध्यका =28

प्रश्न 3
निम्नलिखित सारणी से मध्यका ज्ञात कीजिए

हल:

मध्यका का आकार 21वें पद का मूल्य संचयी आवृत्ति 27 में निहित है और यह संचयी आवृत्ति 15-20 वर्ग में स्थित है; अत: मध्यका का मूल्य इस वर्ग के अन्तर्गत ही स्थित होगा।

निश्चित उत्तरीय प्रश्न (1 अंक)

प्रश्न 1
‘मध्यका’ (माध्यिका) का अर्थ एवं परिभाषा दीजिए। [2008, 14]
उत्तर:
मध्यका आरोही अथवा अवरोही क्रम में अनुविन्यसित समंकमाला के विभिन्न पदों के मध्य का मूल्य होती है और वह समंकमाला को दो भागों में इस प्रकार बाँटती है कि उसके एक ओर के सब पद उससे कम मूल्य के तथा दूसरी ओर के सब पद उससे अधिक मूल्य के होते हैं।

प्रश्न 2
यदि आँकड़ों की संख्या सम (Even) हो तो मध्यका ज्ञात कीजिए।
उत्तर:

प्रश्न 3
यदि आँकड़ों की संख्या विषम हो तो मध्यका ज्ञात कीजिए।
उत्तर:
मध्यका = [latex]\frac { N=1 }{ 2 }[/latex] th

प्रश्न 4
एक छात्र के नौ प्रश्न-पत्रों में निम्नलिखित प्राप्तांक थे
65, 36, 58, 62, 42, 40, 72, 82, 25 प्राप्तांकों की मध्यका ज्ञात कीजिए।
हल:
प्राप्तांकों को आरोही क्रम में व्यवस्थित करने पर,
25, 36, 40, 42, 58, 62, 65, 72, 82
यहाँ, N = 9 अर्थात् पदों की संख्या विषम है।

प्रश्न 5
एक कार्यालय के दस कर्मचारियों का दैनिक वेतन (₹ में) निम्नलिखित है
10, 13, 22, 25, 8, 11, 19, 17, 31, 36.
हल:
यहाँ, N = 10 अर्थात् पदों की संख्या सम है।

बहुविकल्पीय प्रश्न (1 अंक)

प्रश्न 1
किसी भी सांख्यिकीय श्रेणी का मध्य मूल्य होता है
(क) समान्तर माध्य
(ख) मध्यका
(ग) बहुलक
(घ) इनमें से कोई नहीं
उत्तर:
(ख) मध्यका।

प्रश्न 2
केन्द्रीय प्रवृत्ति की माप के अन्तर्गत श्रेणी के मूल्यों को क्रमबद्ध करना आवश्यक होता है
(क) समान्तर माध्य में
(ख) मध्यका में
(ग) बहुलक में
(घ) इनमें से किसी में नहीं
उत्तर:
(ख) मध्यका में।

प्रश्न 3
श्रेणी को दो बराबर भागों में बाँटने वाला मूल्य कहलाता है
(क) समान्तर माध्य
(ख) बहुलक
(ग) मध्यका
(घ) इनमें से कोई नहीं
उत्तर:
(ग) मध्यका।

प्रश्न 4
अविच्छिन्न अथवा सतत् श्रेणी में मध्यका निकालने का सूत्र है

उत्तर:

प्रश्न 5
एक परिवार के 8 सदस्यों की आयु (वर्षों में) निम्नवत है
2,   5,   8,   11,   31,   35,   55 तथा  59
(क) 8
(ख) 11
(ग) 21
(घ) 31
उत्तर:
(ग) 21

प्रश्न 6
निम्न समंकों में माध्यिका क्या है? [2015]
8, 10, 12, 13, 15, 17, 20
(क) 10
(ख) 13
(ग) 15
(घ) 20
उत्तर:
(ख) 13

प्रश्न 7
तोरण वक्रों का प्रतिच्छेदन बिन्दु प्रदर्शित करता है [2009]
(क) समान्तर माध्य
(ख) गुणोत्तर माध्य
(ग) माध्यिका
(घ) बहुलक
उत्तर:
(ग) माध्यिका।