UP Board Solutions for Class 12 Economics Chapter 29 Measure of Central Tendency: Mode (केन्द्रीय प्रवृत्ति की माप : बहुलक)
UP Board Solutions for Class 12 Economics Chapter 29 Measure of Central Tendency: Mode (केन्द्रीय प्रवृत्ति की माप : बहुलक)
विस्तृत उत्तरीय प्रश्न (6 अंक)
प्रश्न 1
बहुलक या भूयिष्ठक किसे कहते हैं? इसको परिभाषित करते हुए इसके गुण व दोषों पर प्रकाश डालिए। बहुलक की विशेषताओं और उपयोग को भी संक्षेप में लिखिए। [2010]
या
बहुलक का अर्थ स्पष्ट कीजिए। बहुलक के गुणों और दोषों को समझाइए। [2013, 16]
उत्तर:
बहुलक या भूयिष्ठक को अंग्रेजी में ‘Mode’ कहते हैं। इसकी उत्पत्ति फ्रेंच भाषा के शब्द, ‘La Mode’ से हुई है जिसका शाब्दिक अर्थ रिवाज या फैशन या प्रचलन है।
सांख्यिकी में बहुलक या भूयिष्ठक से तात्पर्य किसी समंकमाला की सर्वाधिक आवृत्ति वाली माप से होता है। बहुलक एक स्थिति सम्बन्धी प्रमुख माध्य है।
कुछ प्रमुख विद्वानों द्वारा दी गयी परिभाषाएँ निम्नलिखित हैं
क्रॉक्सटन एवं क्राउडेन के शब्दों में, “बहुलक किसी समंक श्रेणी का वह मूल्य है जिसके चारों ओर श्रेणी की इकाइयों के केन्द्रित होने की प्रवृत्ति पायी जाती है और यह मूल्य श्रेणी के मूल्यों का सर्वश्रेष्ठ प्रतिनिधि होता है।”
केनी के अनुसार, “सांख्यिकी में बहुलक उस मान को कहते हैं, जो समंकमाला में सबसे अधिक बार आता है।”
बॉडिंगटन के अनुसार, “बहुलक को महत्त्वपूर्ण प्रकार, रूप या पद के आकार या सर्वाधिक घनत्व की स्थिति के रूप में परिभाषित किया जा सकता है।”
बहुलक के गुण – बहुलक के प्रमुख गुण निम्नलिखित हैं
- थोड़े मदों की जानकारी से भी भूयिष्ठक की गणना सम्भव है। बहुलक की गणना के लिए सभी मदों की आवृत्तियाँ जानना भी आवश्यक नहीं है। केवल बहुलक वर्ग के पहले व बाद वाले वर्ग की आवृत्तियाँ ही पर्याप्त हैं।
- इसके मूल्य पर चरम मदों का प्रभाव नहीं पड़ता, क्योंकि यह सभी मूल्यों पर आधारित नहीं होता।
- भूयिष्ठक मूल्य के चारों ओर समंक श्रेणी के अधिकतम मूल्य केन्द्रित होते हैं; अत: इससे समूह के लक्षणों तथा रचना पर भी प्रकाश पड़ता है।
- बहुलक एक व्यावहारिक माध्य है, जिसका सार्वभौमिक उपयोग है। दैनिक उपयोग की वस्तुएँ; जैसे बनियान, कॉलर या जूते का निर्माता सभी नम्बर के बनियान, कॉलर या जूते नहीं बनाता, वरन् जो नम्बर अधिक माँगे जाते हैं उन्हीं को अधिक बनाता है। यह बहुलक द्वारा ही ज्ञात किया जा सकता है कि किस प्रकार की वस्तु का अधिक निर्माण किया जाए।
- बहुलक का निर्धारण बिन्दुरेखीय रीति से भी सम्भव है।
- बहुलक को समझना व प्रयोग करना दोनों सरल हैं।
- समूह में से चाहे जितने नमूने लिये जाएँ उनसे प्राप्त भूयिष्ठक या बहुलक समान ही रहता है।
बहुलक के दोष – बहुलक के दोष निम्नलिखित हैं
- बहुलक को यदि पदों की संख्या से गुणा किया जाए तो पदों के कुल मूल्यों का योग प्राप्त नहीं किया जा सकता।
- इसमें पदों को क्रमानुसार रखना आवश्यक है। इसके बिना बहुलक ज्ञात करना सम्भव नहीं होता।
- जब श्रेणी के सभी मूल्यों की आवृत्तियाँ समान हों तो बहुलक ज्ञात नहीं किया जा सकता।
- अनेक बार असमान आवृत्ति वितरण में बहुलक सुनिश्चित रूप से निर्धारित नहीं किया जा सकता, क्योंकि ऐसी श्रेणियों में कभी-कभी दो या अधिक बहुलक होते हैं।
- बहुलक का निर्धारण पूर्णतः पदों की आवृत्तियों पर ही आश्रित होने के कारण इससे कभी-कभी बड़े अशुद्ध तथा भ्रमात्मक निष्कर्ष प्राप्त हो जाते हैं। उदाहरणार्थ, किसी टीम द्वारा खेले गये 12 मैचों में 5 में गोल संख्या शून्य रही तथा अन्य मैचों में एक से अधिक गोल किये गये। किन्तु उनमें से किसी भी मैच की गोल संख्या समान नहीं थी। ऐसी दशा में शून्य पद की सबसे अधिक आवृत्ति होने के कारण बहुलक को मूल्य शून्य हो जाएगा।
- भूयिष्ठक के निर्धारण में सीमान्त पदों पर विचार नहीं किया जाता। अतएव जहाँ माध्य निर्धारण में सभी पदों को महत्त्व दिया जाना हो वहाँ बहुलक उपयुक्त माध्य नहीं है।
- बहुलक को बीजगणितीय विवेचन नहीं किया जा सकता; अत: यह अपूर्ण है।
बहुलक की विशेषताएँ – बहुलक की प्रमुख विशेषताएँ निम्नलिखित हैं
- बहुलक के लिए बीजगणितीय विवेचन करना आवश्यक नहीं होता।
- बहुलक आसानी से ज्ञात किया जा सकता है।
- सर्वाधिक घनत्व वाला बिन्दु होने के कारण भूयिष्ठक सम्बद्ध समंकों का यथार्थ प्रतिनिधित्व करता है।
- वास्तविक बहुलक के निर्धारण के लिए पर्याप्त गणना की आवश्यकता होती है। यदि आवृत्ति-वितरण अनियमित हो तो बहुलक का निर्धारण करना भी कठिन हो जाता है।
- भूयिष्ठक पर श्रेणी के असाधारण सीमान्त पदों का कोई प्रभाव नहीं पड़ता।
बहुलक का उपयोग – बहुलक के प्रमुख उपयोग निम्नलिखित हैं
- बहुलक समझने में सरल होता है इसलिए व्यापारिक क्षेत्र में और दैनिक जीवन में इसका अधिक प्रयोग किया जाता है।
- व्यापार एवं उद्योगों के लिए पूर्वानुमान लगाने में बहुलक से अत्यधिक सहायता मिलती है।
- किसी भी वस्तु का औसत आकार ज्ञात करने हेतु बहुलक का प्रयोग किया जाता है।
- बहुत-से व्यवसायी बहुलक के आधार पर ही माल का निर्माण करते हैं; जैसे-टोपी, जूता, हैट, कॉलर आदि।
- उद्योग के क्षेत्रों में माँग को ध्यान में रखकर इसके आधार पर उत्पादन किया जाता है।
- मशीनों द्वारा आजकल बहुलक द्वारा निर्देशित उत्पादन पर जोर दिया जाने लगा है।
- इसी प्रकार मौसमी अध्ययनों में तापमान, वर्षा, वायुगति की औसत मात्रा का निर्धारण बहुलक द्वारा ही किया जाता है।
बहलक की गणना
बहुलक की गणना निम्नलिखित रीतियों से की जाती है
(क) व्यक्तिगत श्रेणी में बहुलक की गणना – व्यक्तिगत श्रेणी में बहुलक की गणना करते समय बहुलक का निरीक्षण द्वारा ही पता लगा लिया जाता है। श्रेणी का जो पद-मूल्य सबसे अधिक बार श्रेणी में आता है, वही पद-मूल्य बहुलक होता है।
व्यक्तिगत श्रेणी में बहुलक ज्ञात करने के लिए सर्वप्रथम पदों को आरोही या अवरोही क्रम में व्यवस्थित कर लेते हैं। पदों के व्यवस्थित होने पर सरलता से पता लग जाता है कि श्रेणी में किस पद-मान की आवृत्ति सबसे अधिक है। श्रेणी में सर्वाधिक पद-मान वाला ही भूयिष्ठक होगा।
उदाहरण 1
माध्यमिक शिक्षा परिषद, उत्तर प्रदेश की कक्षा 12 की परीक्षा में अर्थशास्त्र विषय में 10 परीक्षार्थियों के प्राप्तांक निम्नलिखित हैं
60, 38, 45, 60, 33, 40, 60, 25, 33, 75.
इन समंकों से बहुलक की गणना कीजिए।
हल:
पदों को आरोही क्रम में व्यवस्थित करने पर श्रेणी निम्नवत् प्राप्त होती है
25, 33, 33, 38, 40, 45, 60, 60, 60, 75
उपर्युक्त श्रेणी को देखने से ही यह स्पष्ट हो जाता है कि इस श्रेणी में पद-मान 60 की आवृत्ति सर्वाधिक हैं; अत: बहुलक 60 अंक है।
विशेष – जब किसी व्यक्तिगत श्रेणी में पद-मूल्यों की संख्या बहुत अधिक होती है तो निरीक्षण द्वारा बहुलक ज्ञात करना कठिन होता है। इस प्रकार की स्थिति में बहुलक ज्ञात करने के लिए
उदाहरण 2
में बतायी गयी पद्धति का प्रयोग किया जाता है। उदाहरण 2 निम्नांकित प्राप्तांकों से बहुलक ज्ञात कीजिए
17, 25, 28, 30, 20, 22, 30, 24, 27, 30, 21, 22, 26, 25, 21, 30, 22, 17, 18, 30, 18.
हल:

उपर्युक्त तालिका से स्पष्ट होता है कि 30 अंकों की आवृत्ति सर्वाधिक 5 बार हुई है; अत: बहुलक 30 अंक है।
(ख) खण्डित श्रेणी में बहुलक ज्ञात करना – खण्डित श्रेणी में भी बहुलक ज्ञात करना बहुत सरल है। श्रेणी में जिस पद की बारम्बारता सर्वाधिक होती है, वही पद बहुलक होता है।
उदाहरण 3
माध्यमिक शिक्षा परिषद्, उत्तर प्रदेश कक्षा 12; अर्थशास्त्र की परीक्षा में परीक्षार्थियों ने निम्नलिखित अंक प्राप्त किये, इस श्रेणी का बहुलक ज्ञात कीजिए

हल:
उपर्युक्त श्रेणी में प्राप्तांक 60 की बारम्बारता सबसे अधिक 15 है, अर्थात् 15 परीक्षार्थियों ने 60 अंक प्राप्त किये हैं; अतः स्पष्ट है कि इस श्रेणी का बहुलक 60 अंक है।
उदाहरण 4
बी० एम० एम० इण्टर कॉलेज के विद्यार्थियों की संख्या उनकी आयु के साथ निम्नलिखित सारणी में दी गयी है। इस श्रेणी का बहुलक ज्ञात कीजिए

हल:
उपर्युक्त श्रेणी में सबसे अधिक बारम्बारता 40 है, जो 2 बार आयी है; अतः इस प्रकार की स्थिति में यह निश्चित करना कठिन हो जाता है कि इस श्रेणी का बहुलक 13 है अथवा 15 । इसे ज्ञात करने के लिए समूहन विधि को उपयोग में लाते हैं।
समूहन विधि – समूहन विधि में हमें स्तम्भ बनाने होते हैं। पहला स्तम्भ दी हुई बारम्बारता का होता है। दूसरा स्तम्भ दो-दो आवृत्तियों को जोड़कर बनाया जाता है। तीसरे स्तम्भ को बनाते समय पहली आवृत्ति को छोड़कर शेष दो-दो आवृत्तियों को जोड़कर समूह बनाये जाते हैं। अन्त में दो से कम आवृत्ति बचने पर उसे छोड़ दिया जाता है। चौथे स्तम्भ में पहली आवृत्ति से आरम्भ करके तीन-तीन
आवृत्तियों को जोड़कर समूह बनाये जाते हैं। इसी प्रकार पाँचवे स्तम्भ में पहली आवृत्ति को छोड़कर तीन-तीन आवृत्तियों को जोड़कर समूह बनाये जाते हैं तथा छठे स्तम्भ को बनाते समय प्रथम दो आवृत्तियों को छोड़कर तीन-तीन आवृत्तियों को जोड़कर समूह बनाये जाते हैं। अन्त में यदि तीन से कम आवृत्तियाँ बचे तो उन्हें छोड़ दिया जाता है। यह सारणी अग्रलिखित रूप में बनायी जाती है
समूहन सारणी

उपर्युक्त समूह में यह देखना है कि प्रत्येक स्तम्भ में कौन-सी बारम्बारता सर्वाधिक है। सबसे अधिक बारम्बारता को निम्नलिखित सारणी में अंकित किया गया है
विश्लेषण सारणी
स्तम्भ संख्या प्रत्येक स्तम्भ के अधिकतम बारम्बारता वाले पदचिह्न लगाये गये हैं।

उपर्युक्त सारणी को देखने से यह स्पष्ट होता है कि 13 वह संख्या है जिसकी आवृत्ति सबसे अधिक है; अतः दी हुई श्रेणी की बहुलक 13 है।
(ग) सतत श्रेणी में बहलक ज्ञात करना – सतत् श्रेणी में बहुलक ज्ञात करने के लिए सर्वप्रथम सर्वाधिक आवृत्ति वाला वर्ग ज्ञात किया जाता है। इसे ही बहुलक वर्ग कहते हैं। यदि सारणी में सर्वाधिक बारम्बारता वाला एक ही वर्ग होता है, तब उसमें निम्नलिखित सूत्र के द्वारा बहुलक ज्ञात किया जाता है

यहाँ पर, z = बहुलक (Mode),
L1 = बहुलक वर्ग की निम्न सीमा, L2 = बहुलक वर्ग की उच्च सीमा,
f1 = बहुलक वर्ग की आवृत्ति, f0 = बहुलक वर्ग के पूर्व वर्ग की आवृत्ति,
f2 = बहुलक वर्ग के बाद वाले वर्ग की आवृत्ति।
उदाहरण 5
निम्नलिखित सारणी के आँकड़ों से बहुलक ज्ञात कीजिए

हल:
उपर्युक्त सारणी को देखने से ही पता लग जाता है कि 30-40 वर्गान्तर की आवृत्ति सबसे अधिक है, अत: बहुलक इसी वर्गान्तर में स्थित होगा।
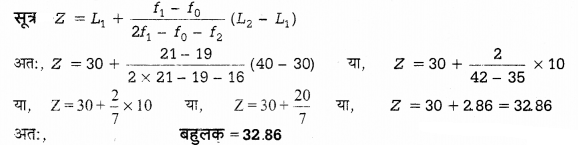
विशेष – सतत् श्रेणी में यदि सबसे अधिक आवृत्ति वाले एक से अधिक वर्ग हों तब सर्वप्रथम समूहन विधि की सहायता से सबसे अधिक आवृत्ति वाला वर्ग ज्ञात करते हैं और उसके बाद निम्नलिखित सूत्र का प्रयोग किया जाता है
![]()
उदाहरण 6
निम्नलिखित सारणी से बहुलक की गणना कीजिए

हल:
इस श्रेणी में 9 आवृत्ति वाले दो वर्ग हैं; अत: सबसे पहले समूहन विधि द्वारा सही बहुलक वर्ग ज्ञात किया जाएगा।

विश्लेषण सारणी

विश्लेषण तालिका से स्पष्ट है कि बहुलक (Mode) 40-50 वर्ग में स्थित है।

विशेष – प्रायः बहुलक की गणना करने के लिए इसी सूत्र का प्रयोग किया जाता है, लेकिन कभी-कभी ऐसा भी होता है कि विश्लेषण सारणी से जो बहुलक वर्ग निकलता है, बहुलक मूल्य का परिकलन इस सूत्र के द्वारा करने पर बहुलक मूल्य, बहुलक वर्ग के बाहर आने लगता है। ऐसी स्थिति में बहुलक मूल्य की गणना करने के लिए 2= L1 + [latex]\frac { { f }_{ 2 } }{ { f }_{ 0 }-{ f }_{ 2 } }[/latex] (L2 – L1) का प्रयोग करते हैं। संकेतों के चिह्न पूर्व सूत्र के अनुसार ही प्रयुक्त होते हैं।
लघु उत्तरीय प्रश्न (4 अंक)
प्रश्न 1
निम्नलिखित सारणी से बहुलक ज्ञात कीजिएप्राप्तांक

हल:

विश्लेषण सारणी

अतः, बहुलक = 28 अंक
प्रश्न 2
निम्नलिखित आँकड़ों से बहुलक ज्ञात कीजिए

हल:
निरीक्षण से स्पष्ट है कि 30-35 वर्गान्तर की आवृत्ति सबसे अधिक है; अत: बहुलक इस वर्गान्तर में ही स्थित होगा।

प्रश्न 3
निम्नलिखित आँकड़ों से बहुलक ज्ञात कीजिए

हल:
निरीक्षण द्वारा स्पष्ट है कि 30-40 वर्गान्तर की आवृत्ति सबसे अधिक है; अत: बहुलक इसी वर्गान्तर में स्थित होगा।

अतिलघु उत्तरीय प्रश्ता (2 अंक)
प्रश्न 1
निम्नलिखित बंटन का बहुलक ज्ञात कीजिए

हल:
यहाँ अधिकतम बारम्बारता 23 है; अत: बहुलक वर्ग 12-15 हुआ।

प्रश्न 2
निम्नलिखित बारम्बारता बंटन का बहुलक ज्ञात कीजिए

हल:
स्पष्ट है कि 45 की बारम्बारता 15 है तथा किसी भी दूसरे पद की बारम्बारता 15 तथा 15 से अधिक नहीं है।
अतः अभीष्ट बहुलक = 45
निश्चित उत्तरीय प्रश्न (1 अंक)
प्रश्न 1
2, 2, 3, 2, 1 का बहुलक बताइए।
उत्तर:
बहुलक = 2.
प्रश्न 2
आँकड़ों 2, 1, 1, 3, 4, 2, 1, 1, 4, 4, 1, 1 का बहुलक बताइए।
उत्तर:
बहुलक = 1
प्रश्न 3
45 शिक्षार्थियों वाली कक्षा में 5 शिक्षार्थियों की ऊँचाई 142 सेमी, 10 शिक्षार्थियों की ऊँचाई 144 सेमी, 10 शिक्षार्थियों की ऊँचाई 146 सेमी, 15 शिक्षार्थियों की ऊँचाई 150 सेमी है तो 5 शिक्षार्थियों की ऊँचाई का बहुलक बताइए।
उत्तर:
बहुलक = 15.
प्रश्न 4
निम्नलिखित आँकड़ों का बहुलक ज्ञात कीजिए
(i) 13, 14, 10, 12, 11, 12, 13, 20, 18, 12, 10, 12.
उत्तर:
बहुलक = 12
(ii) 19, 25, 36, 28, 20, 18, 38, 3, 38, 22, 38, 38.
उत्तर:
बहुलक = 38.
प्रश्न 5
बहुलक का क्या व्यावहारिक प्रयोग है?
उत्तर:
उत्पादन व्यापार एवं उद्योगों में बहुलक का अत्यधिक प्रयोग किया जाता है।
प्रश्न 6
एक अखण्डित (सतत्) श्रेणी के लिए बहुलक ज्ञात करने का सूत्र लिखिए। [2008]
उत्तर:

प्रश्न 7
बहुलक का क्या तात्पर्य है? [2007]
या
बहुलक क्या है? [2012]
उत्तर:
सांख्यिकी आँकड़ों में जिस पद की बारम्बारता अधिकतम हो वह पद बहुलक कहलाता है।
प्रश्न 8
माध्य, माध्यिका और बहुलक में सम्बन्ध बताइए।
उत्तर:
बहुलक = 3 x माध्यिका – 2 x समान्तर माध्य
अर्थात् Z = 3M – 2[latex]\overline { X }[/latex]
प्रश्न 9
बहुलक के दो गुण बताइए।
उत्तर:
बहुलक के दो गुण निम्नलिखित हैं
- बहुलक सबसे सरल माध्य है जो आसानी से समझ में आ जाता है,
- लेखा चित्र द्वारा भी इसे ज्ञात कर लिया जाता है।
प्रश्न 10
बारम्बारता वक्र पर बहुलक कैसे ज्ञात किया जाता है?
उत्तर:
बारम्बारता वक्र का बहुलक क्षैतिज पैमाने पर वह मान होता है जिस पर वक्र की ऊँचाई अधिकतम होती है।
बहुविकल्पीय प्रश्न (1 अंक)
प्रश्न 1
2, 2, 2, 3, 5, 5, 5, 6, 6, 6, 8, 8, 8, तथा 5 का बहुलक होगा
(क) 2
(ख) 6
(ग) 8
(घ) 5
उत्तर:
(घ) 5.
प्रश्न 2
दिये गये आँकड़ों में सबसे अधिक बार आने वाले पद को कहते हैं
(क) समान्तर माध्य
(ख) बहुलक
(ग) माध्यिको
(घ) इनमें से कोई नहीं
उत्तर:
(ख) बहुलक।
प्रश्न 3
वर्गान्तर श्रेणी में बहुलक का सूत्र है

उत्तर:
![]()
प्रश्न 4
माध्य, माध्यिका और बहुलक के सम्बन्ध का सूत्र है

उत्तर:
(ख) Z = 3M – 2[latex]\overline { X }[/latex].
प्रश्न 5
सभी चर मानों पर आधारित केन्द्रीय प्रवृत्ति की माप कौन-सी है? [2007]
(क) बहुलक
(ख) माध्यिका
(ग) समान्तर माध्यिका
(घ) मानक विचलन
उत्तर:
(क) बहुलक।
प्रश्न 6
केन्द्रीय प्रवृत्ति की माप है [2014]
(क) समान्तर माध्य
(ख) माध्यिका
(ग) बहुलक
(घ) इनमें से कोई नहीं
उत्तर:
(घ) इनमें से कोई नहीं।