UP Board Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry
UP Board Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry
प्रश्नावली 11.1
प्रश्न 1.
यदि एक रेखा x,y और z-अक्ष के साथ क्रमश: 90°, 135°, 45° के कोण बनाती है तो इसकी दिक् कोसाइन ज्ञात कीजिए।
हल-
माना रेखा की दिक् कोसाइन क्रमशः l, m, n हैं, तब
l = cos 90°, m = cos 135°, n = cos 45°
l = 0, 
प्रश्न 2.
एक रेखा की दिक् कोसाइन ज्ञात कीजिए जो निर्देशाक्षों के साथ समान कोण बनाती है।
हल-
माना रेखा निर्देशाक्षों के साथ समान कोण α बनाती है, क्ब रेखा की दिक् कोसाइन
l = cosα, m = cos α, n = cos α
परन्तु l² + m² + n² = 1
⇒ cos²α + cos²α + cos²α = 1
प्रश्न 3.
यदि एक रेखा के दिक्-अनुपात – 18, 12, – 4 हैं तो इसकी दिक्-कोज्याएँ क्या हैं?
हल-
दिया है, a = – 18, b = 12, c = – 4
प्रश्न 4.
दर्शाइए कि बिन्दु (2, 3, 4), (-1, -2, 1), (5, 8, 7) संरेख हैं।
हल-
बिन्दुओं P (2, 3, 4) और Q(-1, -2, 1) को मिलाने वाली रेखा के दिक् अनुपात
( – 1 – 2), ( – 2 – 3), (1 – 4) अर्थात् – 3, – 5, – 3 हैं।
बिन्दुओं Q(-1,-2, 1) और R(5, 8, 7) को मिलाने वाली रेखा के दिक् अनुपात 5-(-1), 8-(-2), 7-1 अर्थात् 6, 10, 6 हैं।
∴PQ और QR के दिक् अनुपात समानुपाती हैं।
∴PQ और QR समान्तर हैं।
पुन: चूँकि PQ और QR में बिन्दु Q उभयनिष्ठ है।
अतः P, Q और R संरेख बिन्दु हैं।
प्रश्न 5.
एक त्रिभुज की भुजाओं की दिक् कोसाइन ज्ञात कीजिए। यदि इसके शीर्ष बिन्दु (3, 5, -4), (-1,1, 2) और (-5, – 5, – 2) हैं।
हल-
माना त्रिभुज की भुजाओं के शीर्ष बिन्दु क्रमशः A(3, 5, -4), B(-1, 1, 2) और C(-5, -5, -2) हैं।
प्रश्नावली 11.2
प्रश्न 1.
दर्शाइए कि दिक्-कोज्याएँ
वाली तीन रेखाएँ परस्पर लम्बवत् हैं।
हल-
दो रेखाएँ जिनकी दिक्-कोज्याएँ क्रमशः l1, m1, n1 और l2, m2, n2 परस्पर लम्बवत् होंगी
यदि l1l2 + m1m2 + n1n2 = 0
प्रश्न 2.
दर्शाइए कि बिन्दुओं (1,-1, 2), (3,4,-2) से होकर जाने वाली रेखा बिन्दुओं (0,3,2) और (3, 5, 6) से जाने वाली रेखा पर लम्ब है।
हल-
दिए गए बिन्दु A (1, – 1, 2), B (3,4, -2) से होकर जाने वाली रेखा के दिक्-अनुपात 3 – 1, 4 + 1, -2 – 2 या 2, 5, -4 हैं।
बिन्दु C (0, 3,2) और D (3, 5, 6) से होकर जाने वाली रेखा के दिक्-अनुपात 3 – 0, 5 – 3, 6 – 2 या 3, 2, 4 है।।
हम जानते हैं कि रेखाएँ जिनके दिक् अनुपात (a1, b1, c1) तथा (a2, b2, c2) है परस्पर लम्बवत होंगी यदि और केवल
a1a2 + b1b2 + c1c2 = 0
यहाँ a1a2 + b1b2 + c1c2 = 2 x 3 + 5 x 2 + (- 4) x4
= 6 + 10 – 16
= 16 – 16 = 0
अतः रेखा AB तथा CD एक-दूसरे पर लंब हैं।। इति सिद्धम्
प्रश्न 3.
दर्शाइए कि बिन्दुओं (4,7, 8), (2, 3, 4) से होकर जाने वाली रेखा बिन्दुओं (-1, -2, 1) (1, 2, 5) से जाने वाली रेखा के समान्तर हैं।
हल-
बिन्दु A (4, 7, 8), B(2, 3, 4) से होकर जाने वाली रेखा AB के दिक्-अनुपात a1, b1, c1 क्रमशः 2 – 4, 3 – 7, 4 – 8 या -2, -4, -4 हैं।
बिन्दु C (-1, – 2, 1) और D (1, 2, 5) से होकर जाने वाली रेखा CD के दिक्-अनुपात a2, b2, c2, क्रमशः 1 – (-1), 2 – (-2), 5 – 1 या 2, 4, 4 हैं।
अतः AB || CD इति सिद्धम्
प्रश्न 4.
बिन्दु (1, 2, 3) से गुजरने वाली रेखा का समीकरण ज्ञात कीजिए जो सदिश 
हल-
प्रश्न 5.
बिन्दु जिसका स्थिति सदिश 
हल-
प्रश्न 6.
उस रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (-2, 4, -5) से जाती है और
के समान्तर है।
हल-
प्रश्न 7.
एक रेखा का कार्तीय समीकरण
है। इसका सदिश समीकरण ज्ञात कीजिए।
हल-
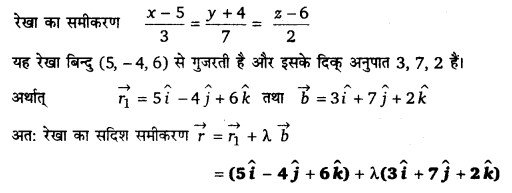
प्रश्न 8.
मूलबिन्दु और (5,-2, 3) से जाने वाली रेखा का समीकरण सदिश व कार्तीय रूपों में ज्ञात कीजिए।
हल-
प्रश्न 9.
बिन्दुओं (3, -2, -5) और (3, -2, 6) से होकर जाने वाली रेखा का समीकरण सदिश व कार्तीय रूप में ज्ञात कीजिए।
हल-
दिये गये बिन्दुओं A(3,-2, -5) व B(3, -2, 6) के स्थिति सदिश ।
प्रश्न 10.
निम्नलिखित रेखायुग्मों के बीच का कोण ज्ञात कीजिए।
हल-
प्रश्न 11.
निम्नलिखित रेखायुग्मों के बीच का कोण ज्ञात कीजिए
हल-
(i) दी गई रेखाओं के दिक् अनुपात क्रमश: 2, 5, -3 और -1, 8, 4 है।
यदि दी गई रेखाओं के मध्य कोण θ है, तब
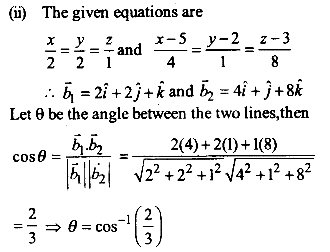
प्रश्न 12.
हल-
प्रश्न 13.
हल-
प्रश्न 14.
हल-
प्रश्न 15.
हल-
प्रश्न 16.
रेखाएँ, जिनके सदिश समीकरण निम्नलिखित हैं, के बीच की न्यूनतम दूरी ज्ञात कीजिए।
हल-
प्रश्न 17.
रेखाएँ, जिनके सदिश समीकरण निम्नलिखित हैं, के बीच की न्यूनतम दूरी ज्ञात कीजिए।
हल-
प्रश्नावली 11.3
प्रश्न 1.
निम्नलिखित प्रश्नों में से प्रत्येक में समतल के अभिलम्ब की दिक् कोसाइन और मूलबिन्दु से दूरी ज्ञात कीजिए।
(a) z = 2
(b) x + y + z = 1
(c) 2x + 3y – z = 5
(d) 5y + 8 = 0
हल-
(a) दिये गये समतल का समीकरण z = 2
इसकी तुलना समतल के मानक समीकरण lx + my + nz = p से करने पर,
समतल की मूलबिन्दु से दूरी
p = 2 मात्रक तथा
समतल के अभिलम्ब की दिक् केसाइन l = 0, m = 0, n = 1
(b) दिये गये समतल का समीकरण x + y + z = 1
प्रश्न 2.
उस समतल का समीकरणे ज्ञात कीजिए जो मूलबिन्दु से 7 मात्रक दूरी पर है, और सदिश 
हल-
यहाँ p = 7 मात्रक
प्रश्न 3.
निम्नलिखित समतलों का कार्तीय समीकरण ज्ञात कीजिए
हल-
प्रश्न 4.
निम्नलिखित स्थितियों में मूलबिन्दु से खींचे गये लम्ब के पाद के निर्देशांक ज्ञात कीजिए।
(a) 2x + 3y + 4z – 12 = 0
(b) 3y + 4z – 6 = 0
(c) x + y + z = 1
(d) 5y + 8 = 0
हल-
(a) माना मूलबिन्दु से समतल पर डाले गये लम्ब के पाद P के निर्देशांक
(x1, y1, z1) हैं, तब रेखा OP के दिक् अनुपात x1, y1, z1 हैं।
समतल के समीकरण को अभिलम्ब रूप में लिखने पर,
प्रश्न 5.
निम्नलिखित प्रतिबन्यों के अन्तर्गत समतलों को सदिश एवं कार्तीय समीकरण ज्ञात कीजिए।
(a) बिन्दु (1, 0, -2) से जाता है और सदिश 
(b) बिन्दु (1, 4, 6) से जाता है और 
हल-
प्रश्न 6.
उन समतलों के समीकरण ज्ञात कीजिए जो निम्नलिखित बिन्दुओं से गुजरते हैं।
(a) (1, 1 ,-1), (6, 4, -5), (-4, -2, 3)
(b) (1, 1, 0), (1, 2, 1), (-2, 2, -1)
हल-
प्रश्न 7.
समतल 2x + y – z = 5 द्वारा काटे गए अन्तःखण्डों को ज्ञात कीजिए।
हल-
प्रश्न 8.
उस समतल का समीकरण ज्ञात कीजिए जिसका y-अक्ष पर अन्त:खण्ड 3 और जो तल ZOX के समान्तर है।
हल-
ZOX के समान्तर तल का समीकरण y = a
यह तल y-अक्ष पर अन्त:खण्ड 3 बनाता है।
⇒ a = 3
समतल अभीष्ट का समीकरण y = 3
प्रश्न 9.
उस समतल का समीकरण ज्ञात कीजिए जो समतलों 3x – y + 2z – 4 = 0 और x + y + z – 2 = 0 के प्रतिच्छेदन तथा बिन्दु (2, 2, 1) से होकर जाता है।
हल-
दिये गये समतलों के प्रतिच्छेदन से जाने वाले समतल का समीकरण
(3x – y + 2z – 4) + λ(x + y + z – 2) = 0 …(1)
यह बिन्दु (2, 2, 1) से होकर जाता है, तब
प्रश्न 10.
हल-
उपरोक्त प्रश्न की भाँति स्वयं हल कीजिए।
प्रश्न 11.
तलों x + y + z = 1 और 2x + 3y + 4z = 5 की प्रतिच्छेदन रेखा से होकर जाने वाले तथा तल x – y + z = 0 पर लम्बवत् तल का समीकरण ज्ञात कीजिए।
हल-
तलों x + y + z = 1 और 2x + 3y + 4z = 5 की प्रतिच्छेदन रेखा से जाने वाले समतल का समीकरण ।
(x + y + z – 1) + λ (2x + 3y + 4z – 5) = 0
(1 + 2λ)x + (1 + 3λ)y + (1 + 4λ)z – 5λ – 1 = 0 ….(1)
समतल (1) तल x – y + z = 0 पर लम्ब है।
(1 + 2λ).(1) + (1 + 3λ).(-1) + (1 + 4λ).(1) = 0
1 + 2λ – 1 – 3λ + 1 + 4λ = 0
प्रश्न 12.
हल-
प्रश्न 13.
निम्नलिखित प्रश्नों में ज्ञात कीजिए कि क्या दिए गए समतलों के युग्म समान्तर हैं अथवा लम्बवत् हैं और उस स्थिति में, जब ये न तो समान्तर हैं और न ही लम्बवत्, उनके बीच का कोण ज्ञात कीजिए।
(a) 7x + 5y + 6z + 30 = 0 और 3x – y – 10z + 4= 0
(b) 2x + y + 3z – 2 = 0 और x – 2y + 5 = 0
(c) 2x – 2y + 4z + 5 = 0 और 3x – 3y + 6z – 1 = 0
(d) 2x – y + 3z – 1 = 0 और 2x – y + 3z + 3 = 0
(c) 4x + 8y + z – 8 = 0 और y + z – 4 = 0
हल-
दिए गए समतल a1x + b1y + c1z + d1 = 0 और a2x + b2y + c2z + d2 = 0 हैं।
प्रश्न 14.
निम्नलिखित प्रश्नों में प्रत्येक दिए गए बिन्दु से दिए गए संगत समतलों की दूरी ज्ञात कीजिए।
हल-
हम जानते है। कि बिन्दु (x1, y1, z1) की समतल ax + by + cz + d = 0 से दूरी
