UP Board Solutions for Class 12 Maths Chapter 3 Matrices

प्रश्नावली 3.1

प्रश्न 1.
आव्यूह $A=\left[ \begin{matrix} 2 \\ 35 \\ \sqrt { 3 } \end{matrix}\begin{matrix} \quad 5 \\ \quad -2 \\ \quad 1 \end{matrix}\quad \begin{matrix} 19 \\ 5/2 \\ -5 \end{matrix}\quad \begin{matrix} -7 \\ 12 \\ 17 \end{matrix} \right]$ के लिए ज्ञात कीजिए
(i) आव्यूह की कोटि
(ii) अवयवों की संख्या
(iii) अवयव a₁₃, a₂₁, a₃₃, a₂₄, a₂₃
हल-
(i) चूँकि आव्यूह में 3 पंक्ति तथा 4 स्तम्भ हैं।
∴ आव्यूह की कोटि = 3×4
(ii) आव्यूह में अवयवों की संख्या = पंक्तियों की संख्या ४ स्तम्भों की संख्या
= 3 x 4 = 12
(iii) अवयव a₁₃ = 19, a₂₁ = 35, a₃₃ = – 5, a₂₄ = 12, a₂₃ = $\frac { 5 }{ 2 }$

प्रश्न 2.
यदि किसी आव्यूह में 24 अवयव हैं तो इसकी सम्भव कोटियाँ क्या हैं ? यदि इसमें 13 अवयव हों, तो कोटियाँ क्या होंगी?
हल-
24 अवयव वाले आव्यूह की सम्भव कोटियाँ होंगी।
1 x 24, 2 x 12, 3 x 8, 4 x 6, 6 x 4, 8 x 3, 12 x 2, 24 x 1
13 अवयव वाले आव्यूह की सम्भव कोटियाँ होंगी
1 x 13, 13 x 1

प्रश्न 3.
यदि किसी आव्यूह में 18 अवयव हैं तो इसकी सम्भव कोटियाँ क्या हैं? यदि इसमें 5 अवयव हों तो क्या होगा?
हल-
18 अवयव वाले आव्यूह की सम्भव कोटियाँ होंगी
1 x 18, 2 x 9, 3 x 6, 6 x 3, 9 x 2, 18 x 1
5 अवयव वाले आव्यूह की सम्भव कोटियाँ होंगी 1 x 5, 5 x 1

प्रश्न 4.
एक 2 x 2 आव्यूह A = [a_ij] की रचना कीजिए जिसके अवयव निम्नलिखित प्रकार से दिए गए हैं।
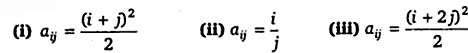
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 1
हल-
एक 2×2 क्रम का आव्यूह होगा |

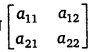
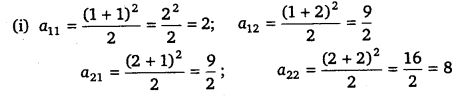
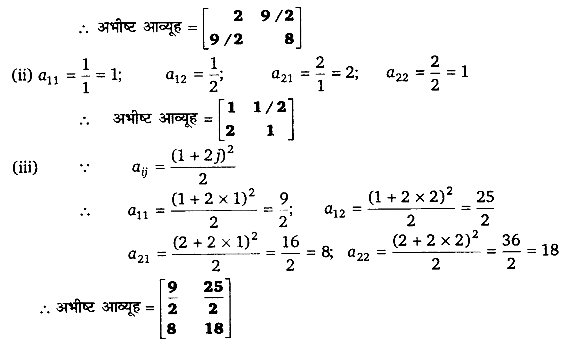
प्रश्न 5
एक 3×4 आव्यूह की रचना कीजिए जिसके अवयव निम्नलिखित प्रकार से प्राप्त होते हैं

हल-
3×4 क्रम का आव्यूह होगा

प्रश्न 6
निम्नलिखित समीकरणों से x,y तथा z के मान ज्ञात कीजिए

हल-
प्रत्येक खण्ड में दिये गए दोनों आव्यूह समान हैं।
(i) दोनों आव्यूहों के संगत अवयवों की तुलना करने पर,
x = 1, y = 4, z = 3
(ii) दोनों आव्यूहों के संगत अवयवों की तुलना करने पर,
x + y = 6 …(1)
5 + z = 5 ⇒ z = 0 …(2)
xy = 8 …(3)
समी० (1) व (3) को हल करने पर, x = 4, y = 2 या x = 2, y = 4
∴ x = 4, y = 2, 3 = 0, या x = 2, y = 4, z = 0
(iii) दोनों आव्यूहों के संगत अवयवों की तुलना करने पर,
x + y + 2 = 9 …(1)
x + 2 = 5 …(2)
y + 2 = 7 …(3)
समी० (2) और समी० (3) को जोड़ने पर, (x + y + z) + z = 12
9 + z = 12 ⇒ z = 3
समी० (2) से, x + 3 = 5 ⇒ x = 2
तथा समी० (3) से, y + 3 = 7 = y =4
अतः x = 2, y = 4, z = 3

प्रश्न 7.
यदि
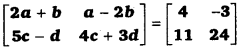
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 8
a,b,c तथा d के मान ज्ञात कीजिए।
हल-
आव्यूह युग्म समान हैं।
संगत अवयवों की तुलना करने पर,
2d + b = 4 …(1)
a – 2b = -3 …(2)
5c – d = 11 …(3)
4c + 3d = 24 …(4)
समी० (1) को 2 से गुणा करके (2) में जोड़ने पर,
5a = 5 ⇒ a = 1
a का मान समी० (1) में रखने पर,
2 x 1 + b = 4 ⇒ b = 4 – 2 = 2
समी० (3) को 3 से गुणा करके (4) में जोड़ने पर,
19c = 57 ⇒ c = 3
c का मान समी० (3) में रखने पर,
5 x 3 – d = 11 ⇒ d = 15 – 11 = 4
∴ a = 1, b = 2, c = 3, d = 4

प्रश्न 8.
A = [a_ij]_mxn एक वर्ग आव्यूह है यदि
(a) m < n
(b) m > n
(c) m = n
(d) इनमें से कोई नहीं।
उत्तर-
∵ वर्ग आव्यूह में पंक्तियों की संख्या स्तम्भों की संख्या के बराबर होती है।
∴ m = n
अत: विकल्प (c) सही है।

प्रश्न 9.
x तथा y के प्रदत्त किन मानों के लिए आव्यूहों के निम्नलिखित युग्म समान हैं ?

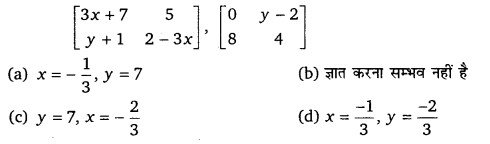
हल-
यदि आव्यूह युग्म समान है तब
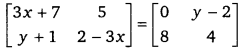
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 10

प्रश्न 10. 3×3 कोटि के ऐसे आव्यूहों की कुल कितनी संख्या होगी जिनकी प्रत्येक प्रविष्टि 0 या 1 है?
(A) 27
(B) 18
(C) 81
(D) 512
हल-
बहुविकल्पीय प्रश्नावली के प्रश्न 2 का हल देखें।

प्रश्नावली 3.2

प्रश्न 1.
मान लीजिए कि
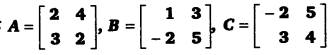
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 12
तो निम्नलिखित ज्ञात कीजिए
(i) A + B
(ii) A – B
(iii) 3A – C
(iv) AB
(v) BA
हल-

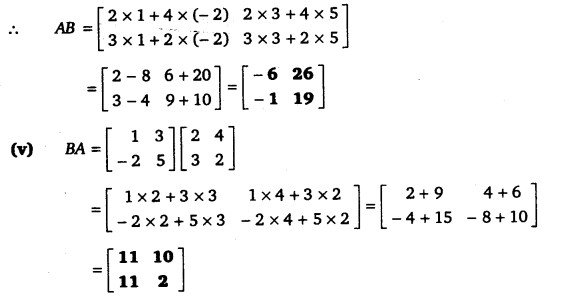
प्रश्न 2
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 15
हल-

प्रश्न 3.
निदर्शित गुणनफल परिकलित कीजिए,

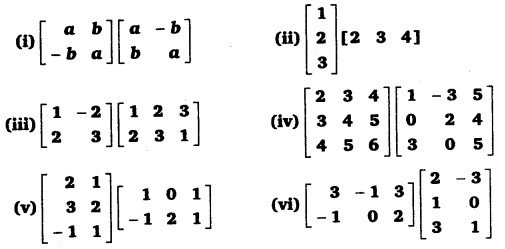
हल
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 18

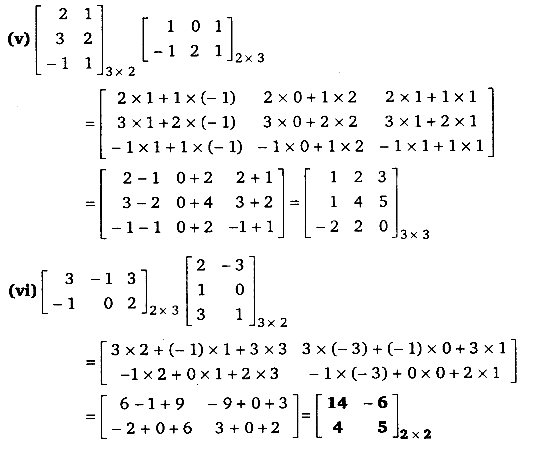
प्रश्न 4.
यदि
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 21
तो (A + B) तथा (B – C) परिकलित कीजिए। साथ ही सत्यापित कीजिए कि A + (B – C) = (A + B) – C
हल-

प्रश्न 5.

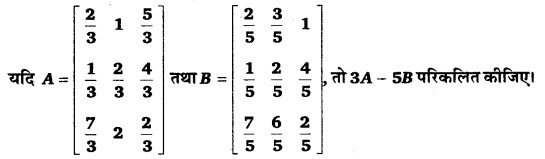
हल-

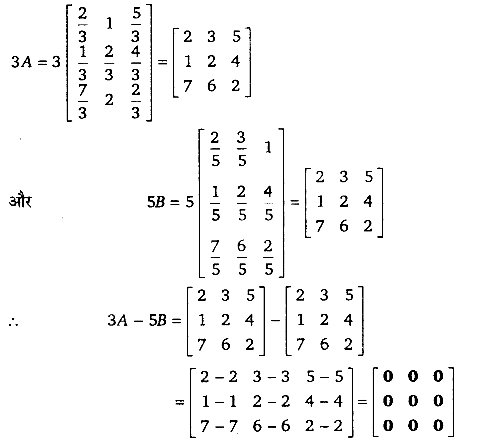
प्रश्न 6.
सरल कीजिए
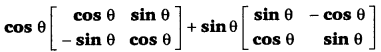
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 26
हल-

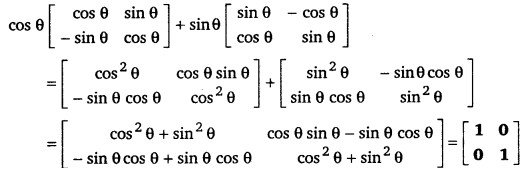
प्रश्न 7.

प्रश्न 8.
X ज्ञात कीजिए यदि $Y=\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix}$ तथा $2X+Y=\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix}$
हल-
$2X+Y=\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix}$ में Y का मान रखने पर,

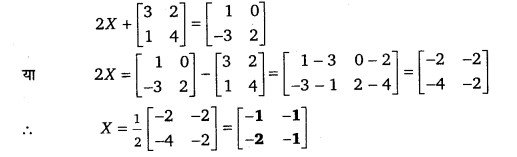
प्रश्न 9.
(i) x तथा y ज्ञात कीजिए यदि $2\begin{bmatrix} 1 & 3 \\ 0 & x \end{bmatrix}+\begin{bmatrix} y & 0 \\ 1 & 2 \end{bmatrix}=\begin{bmatrix} 5 & 6 \\ 1 & 8 \end{bmatrix}$
(ii) x, y, z का मान ज्ञात कीजिए यदि $\begin{bmatrix} 3 & x \\ 4 & y \end{bmatrix}=2\begin{bmatrix} 1.5 & 1 \\ z & 1 \end{bmatrix}$
हल-
(i) प्रश्नानुसार,

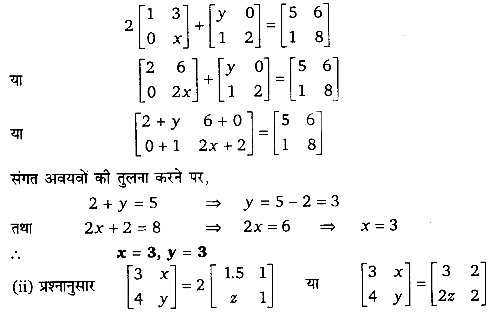
दोनों ओर संगत अवयवों की तुलना करने पर,
x = 2, y = 2, 2z = 4 ⇒ z = 2

प्रश्न 10.
दिये गये समीकरण को x,y,z तथा t के लिए हल कीजिए यदि
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 31
हल-
दिया गया समीकरण

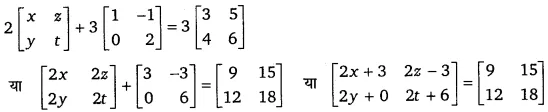
∴ x = 3, y = 6, z = 9,t = 6

प्रश्न 11.
यदि $x\left[ \begin{matrix} 2 \\ 3 \end{matrix} \right] +y\left[ \begin{matrix} -1 \\ 1 \end{matrix} \right] =\left[ \begin{matrix} 10 \\ 5 \end{matrix} \right]$ है, तो x तथा y के मान ज्ञात कीजिए।
हल-

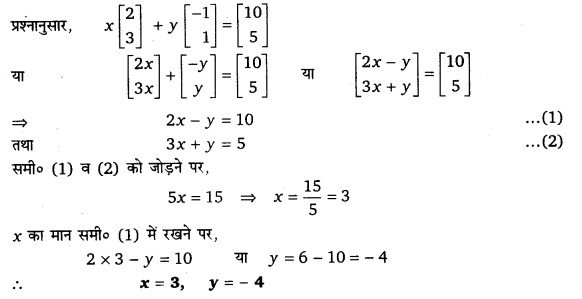
प्रश्न 12.
यदि
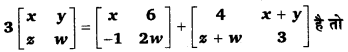
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 35
x,y,z तथा w के मानों को ज्ञात कीजिए।
हल-

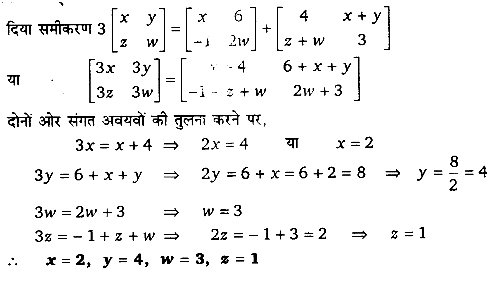
प्रश्न 13.
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 37
हल-

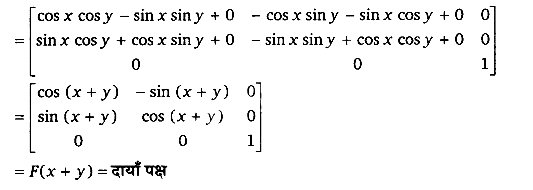
प्रश्न 14. देशइए कि
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 40
हल-

प्रश्न 15.
यदि $A=\left[ \begin{matrix} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{matrix} \right]$ है तो A² – 5A + 6I का मान ज्ञात कीजिए।
हल-

प्रश्न 16. यदि $A=\left[ \begin{matrix} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{matrix} \right]$ है तो सिद्ध कीजिए कि A³ – 6A² + 7A + 2I = 0
हल-

UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 45

प्रश्न 17.
यदि
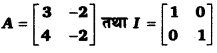
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 46
एवं A² = kA – 2I हो, तो k का मान ज्ञात कीजिए।
हल-
प्रश्नानुसार, A² = kA – 2I

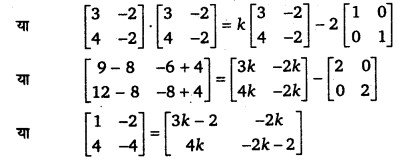
संगत अवयवों की तुलना करने पर,
3k – 2 = 1 या 3k = 3 ⇒ k = 1

प्रश्न 18.
यदि $A=\begin{bmatrix} 0 & \quad -tan\alpha /2 \\ tan\alpha /2 & \quad 0 \end{bmatrix}$ तथा I कोटि का एक तत्समक आव्यूह है, तो सिद्ध कीजिए कि $I+A=(I-A)\begin{bmatrix} cos\alpha & \quad -sin\alpha \\ sin\alpha & \quad cos\alpha \end{bmatrix}$
हल-

प्रश्न 19. किसी व्यापार संघ के पास Rs 30000 का कोष है, जिसे दो भिन्न-भिन्न प्रकार के बांडों में निवेशित करना है। प्रथम बांड पर 5% वार्षिक तथा द्वितीय बांड पर 7% वार्षिक ब्याज प्राप्त होता है। आव्यूह गुणन के प्रयोग द्वारा यह निर्धारित कीजिए कि Rs 30000 के कोष को दो प्रकार के बांडों में निवेश करने के लिए किस प्रकार बाँटें जिससे व्यापार संघ को प्राप्त कुल वार्षिक ब्याज
(a) Rs 1800 हो।
(b) Rs 2000 हो।।
हल-
(a) माना 30000 के दो भाग क्रमश: Rs x तथा Rs (30000 – x) हैं।
आव्यूह A = [x (30000 – x)] से दर्शाते हैं।

UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 50

प्रश्न 20. किसी स्कूल की पुस्तकों की दुकान में 10 दर्जन रसायन विज्ञान, 8 दर्जन भौतिक विज्ञान तथा 10 दर्जन अर्थशास्त्र की पुस्तकें हैं। इन पुस्तकों का विक्रय मूल्य क्रमशः Rs 80, Rs 60 तथा Rs 40 प्रति पुस्तक है। आव्यूह बीजगणित के प्रयोग द्वारा ज्ञात कीजिए कि सभी पुस्तकों को बेचने से दुकान को कुल कितनी धनराशि प्राप्त होगी?
हल-
विद्यालय में पुस्तकों की संख्या
रसायन विज्ञान – 10 दर्जन = 120 पुस्तकें
भौतिक विज्ञान – 8 दर्जन = 96 पुस्तकें
अर्थशास्त्र – 10 दर्जन = 120 पुस्तकें
इसे आव्यूह A = [120 96 120] से प्रदर्शित करते हैं।
रसायन विज्ञान, भौतिक विज्ञान और अर्थशास्त्र की प्रत्येक पुस्तक का विक्रय मूल्य क्रमशः Rs 80, Rs 60 तथा Rs 40 है।

प्रश्न 21.
PY + WY के परिभाषित होने के लिए n,k तथा p पर क्या प्रतिबन्ध होगा?
(a) k = 3, 2 = n
(b) k स्वेच्छ है, p = 2
(c) p स्वेच्छ है, k = 3
(d) k = 2, p = 3
हल-
दिया है, आव्यूह : X, Y, Z, W तथा P की कोटियाँ क्रमश: 2 × n,3 × k, 2 × p, n × 3, p × k हैं।
∴ P की कोटि = p × k तथा Y की कोटि = 3 × k
∴ PY संभव है यदि k = 3
PY की कोटि = p × k = p × 3
W और Y की कोटियाँ क्रमशः n × 3 और 3 × k = 3 × 3
∴ WY की कोटि = n × 3
PY व WY का योग तभी सम्भव है जब यह दोनों एक ही कोटि के हों
∴ p × 3 = n × 3 ⇒ p = n
∴ PY + WY परिभाषित हैं यदि p = n और k = 3
अतः विकल्प (a) सही है।

प्रश्न 22.
यदि n = p, तो आव्यूह 7x – 5z की कोटि है
(a) p × 2
(b) 2 × n
(c) n × 3
(d) p × n
हल-
आव्यूह X तथा Z की कोटियाँ क्रमशः 2 × n और 2 × p हैं।
आव्यूह 7X – 5Z परिभाषित होगा यदि X तथा Z एक ही कोटि के हों, क्योंकि p = n दोनों की कोटि 2 × n है।
अतः विकल्प (b) सही है।

प्रश्नावली 3.3

प्रश्न 1.
निम्नलिखित आव्यूहों में से प्रत्येक का परिवर्त ज्ञात कीजिए
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 52
हल-
पंक्तियों को स्तम्भों में तथा स्तम्भों को पंक्तियों में बदलने पर प्राप्त आव्यूह परिवर्त आव्यूह होंगे।

प्रश्न 2.
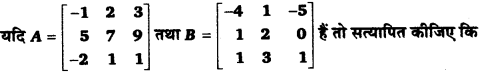
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 54
(i) (A + B)’ = A’ + B’
(ii) (A – B)’ = A’ – B’
हल-

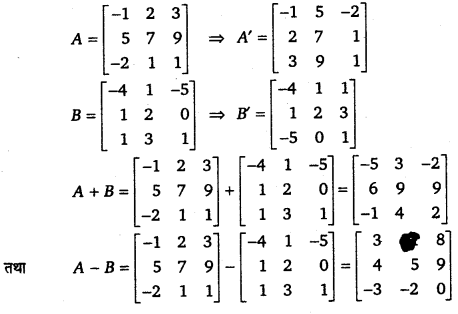
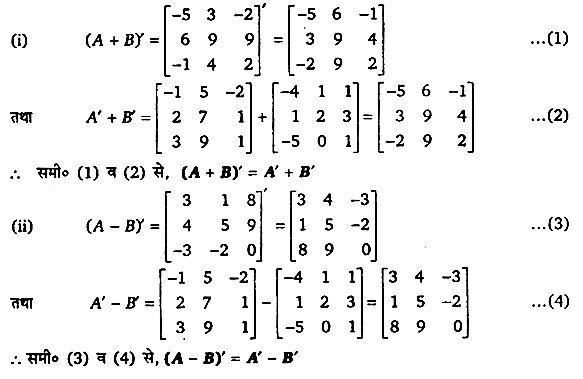
प्रश्न 3.
यदि
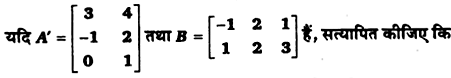
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 57
(i) (A + B)’ = A’ + B’
(ii) (A – B)’ = A’ – B’
हल-

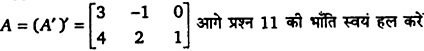
प्रश्न 4.
यदि
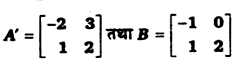
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 59
हैं, तो (A + 2B)’ ज्ञात कीजिए।
हल-

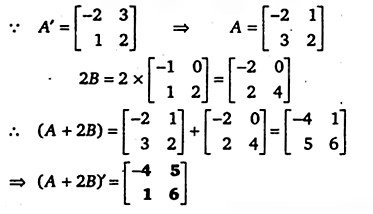
प्रश्न 5. A तथा B आव्यूहों के लिए सत्यापित कीजिए कि (AB)’ = B’A’, जहाँ
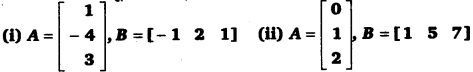
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 61
हल-

प्रश्न 6.
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 63
हल-
(i)

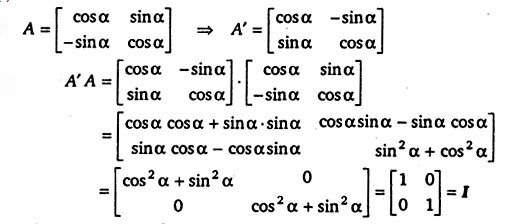
प्रश्न 7.
(i) सिद्ध कीजिए कि आव्यूह $A=\left[ \begin{matrix} 1 & -1 & 5 \\ -1 & 2 & 1 \\ 5 & 1 & 3 \end{matrix} \right]$ एक सममित आव्यूह है।
(ii) सिद्ध कीजिए कि आव्यूह $A=\left[ \begin{matrix} 0 & 1 & -1 \\ -1 & 0 & 1 \\ 1 & -1 & 0 \end{matrix} \right]$ एक विषम सममित आव्यूह है।
हल-

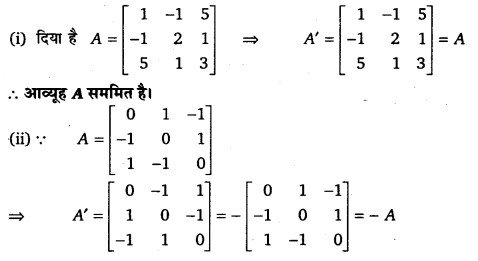
आव्यूह A विषम सममित है।

प्रश्न 8.
आव्यूह, $A=\begin{bmatrix} 1 & 5 \\ 6 & 7 \end{bmatrix}$ के लिए सत्यापित कीजिए कि
(i) (A + A’) एक सममित आव्यूह है।
(ii) (A – A’) एक विषम सममित आव्यूह है।
हल-

प्रश्न 9.
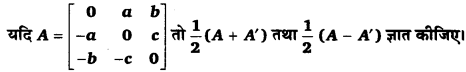
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 68
हल-

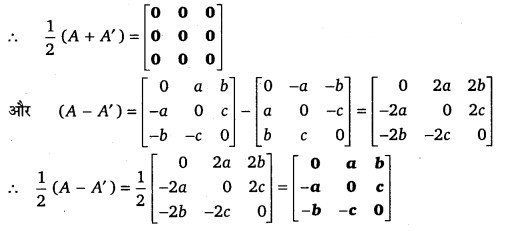
प्रश्न 10.
निम्नलिखित आव्यूहों को एक सममित आव्यूह तथा एक विषम सममित आव्यूह के योगफल के रूप में व्यक्त कीजिए
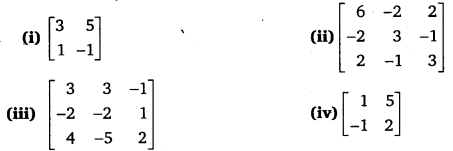
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 71
हल-

प्रश्न संख्या 11 तथा 12 में सही उत्तर चुनिए

प्रश्न 11.यदि A तथा B समान कोटि के सममित आव्यूह हैं तो AB – BA एक
(A) विषम सममित आव्यूह है
(B) सममित आव्यूह है।
(C) शून्य आव्यूह है।
(D) तत्समक आव्यूह है।
हल-
चूँकि A और B समान कोटि की सममित आव्यूह है।

प्रश्न 12.
यदि $A=\begin{bmatrix} cos\alpha & \quad -sin\alpha \\ sin\alpha & \quad cos\alpha \end{bmatrix}$ तथा A + A’ = I, तो α का मान ज्ञात कीजिए।
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 76

प्रश्नावली 3.4

प्रश्न संख्या 1 से 17 तक के आव्यूहों के व्युत्क्रम, यदि उनका अस्तित्व है तो प्रारम्भिक रूपान्तरण के प्रयोग से ज्ञात कीजिए।

प्रश्न 1.
$A=\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}$
हल-
दिया गया आव्यूह $A=\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}$
आव्यूह A को A = IA के रूप में लिखने पर,

प्रश्न 2.
$A=\begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix}$
हल :
प्रश्न 1 की भाँति स्वयं हल कीजिए।

प्रश्न 3.
$A=\begin{bmatrix} 1 & 3 \\ 2 & 7 \end{bmatrix}$
हल-
दिया गया आव्यूह $A=\begin{bmatrix} 1 & 3 \\ 2 & 7 \end{bmatrix}$
आव्यूह A को A = IA के रूप में लिखने पर, |
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 78

प्रश्न 4.

हल-

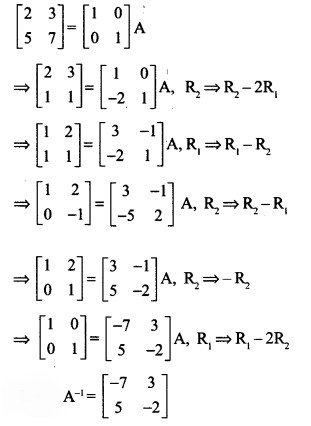
प्रश्न 5.

हल-

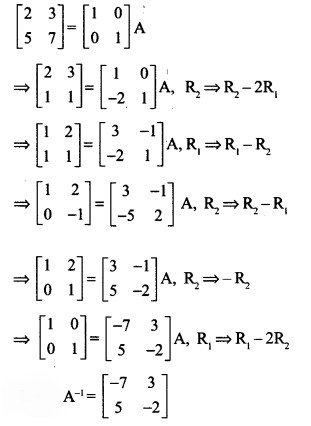
प्रश्न 6.

हल-
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 84

प्रश्न 7.

हल-

प्रश्न 8.

हल-
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 88

प्रश्न 9.

हल-

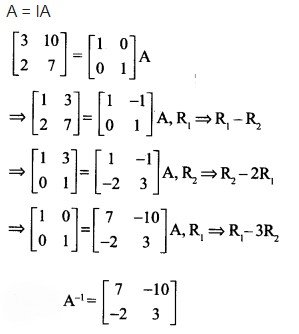
प्रश्न 10.

हल-

प्रश्न 11.

हल-

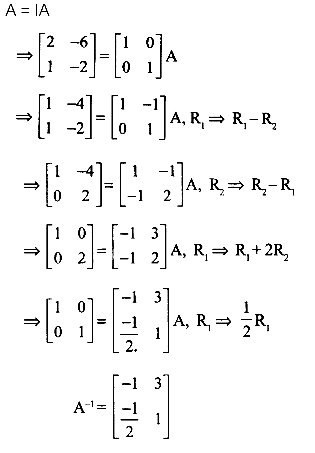
प्रश्न 12.
$A=\begin{bmatrix} 6 & -3 \\ -2 & 1 \end{bmatrix}$
हल-

UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 95
चूंकि पहली पंक्ति में दोनों अवयव शून्य हैं।
∴ A का व्युत्क्रम A^-1 का अस्तित्व नहीं है।

प्रश्न 13

हल-

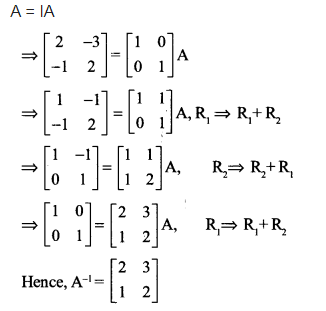
प्रश्न 14

हल-
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 99

प्रश्न 15.
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 100
हल-

प्रश्न 16.
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 103
हल-

प्रश्न 17
UP Board Solutions for Class 12 Maths Chapter 3 Matrices image 106
हल-

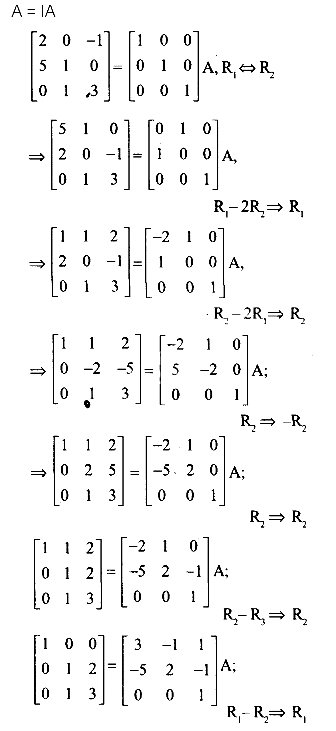
प्रश्न 18.
आव्यूह A तथा B एक-दूसरे के व्युत्क्रम होंगे केवल यदि
(A) AB = BA
(B) AB = BA = 0
(C) AB = 0, BA = I
(D) AB = BA = I
हल-
AB = BA = 1, केवल इस स्थिति में ही आव्यूह A और आव्यूह B एक-दूसरे के व्युत्क्रम होंगे। अत: विकल्प (D) सही है।