UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics (तरंग-प्रकाशिकी)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
589 nm तरंगदैर्ध्य का एकवर्णीय प्रकाश वायु से जल की सतह पर आपतित होता है।
(a) परावर्तित, तथा (b) अपवर्तित प्रकाश की तरंगदैर्घ्य, आवृत्ति तथा चाल क्या होगी?
जल का अपवर्तनांक 1.33 है।
हल-
दिया है, आपतित प्रकाश की तरंगदैर्घ्य
λ₁ = 589 nm = 589 x 10⁹ मीटर
वायु में प्रकाश की चाल c = 3 x 108 मी/से
तथा ${ _{ a }{ \mu }_{ \omega } }$ = 1.33
(a) परावर्तित प्रकाश के लिए
(i) चूंकि परावर्तित प्रकाश की तरंगदैर्घ्य अपरिवर्तित रहती है, अतः परावर्तित प्रकाश की तरंगदैर्घ्य
λ_a = λ₁ = 589 nm
(ii) चूंकि परावर्तन में माध्यम नहीं बदलता अतः परावर्तित प्रकाश की चाल c = 3 x 10⁸ मी/से
(iii) सूत्र c = υλ से
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q1

प्रश्न 2.
निम्नलिखित दशाओं में प्रत्येक तरंगाग्र की आकृति क्या है?
(a) किसी बिन्दु स्रोत से अपसरित प्रकाश।
(b) उत्तल लेन्स से निर्गमित प्रकाश, जिसके फोकस बिन्दु पर कोई बिन्दु स्रोत रखा है।
(c) किसी दूरस्थ तारे से आने वाले प्रकाश तरंगाग्र का पृथ्वी द्वारा अवरोधित (intercepted) भाग।
उत्तर-
(a) जब एक बिन्दु स्रोत से प्रकाश अपसरित होता है, तब तरंगाग्र गोलीय अभिसारी प्रकार का होता है।
(b) जब बिन्दु स्रोत को उत्तल लेन्स के फोकस पर रखा जाता है, तब लेन्स से निर्गत प्रकाश किरणें एक-दूसरे के समान्तर होती हैं तथा तरंगाग्र समतल होता है।
(c) इस स्थिति में तरंगाग्र की आकृति लगभग समतल होती है क्योंकि प्रकाश स्रोत पृथ्वी से दूरस्थ तारा है, अत: बड़े गोले के पृष्ठ पर छोटा क्षेत्रफल लगभग समतल है।

प्रश्न 3.
(a) काँच का अपवर्तनांक 1.5 है। काँच में प्रकाश की चाल क्या होगी? (निर्वात में प्रकाश की चाल 3.0 x 10 m^-1 है।)
(b) क्या काँच में प्रकाश की चाल, प्रकाश के रंग पर निर्भर करती है? यदि हाँ, तो लाल तथा बैंगनी में से कौन-सा रंग काँच के प्रिज्म में धीमा चलता है?
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q3

प्रश्न 4.
यंग के द्विझिरी प्रयोग में झिर्रियों के बीच की दूरी 0.28 mm है तथा परदा 1.4 m की दूरी पर रखा गया है। केन्द्रीय दीप्त फ्रिन्ज एवं चतुर्थ दीप्त फ्रिन्ज के बीच की दूरी 1.2 cm मापी गई है। प्रयोग में उपयोग किए गए प्रकाश की तरंगदैर्घ्य ज्ञात कीजिए।
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q4

प्रश्न 5.
यंग के द्विझिरी प्रयोग में, λ तरंगदैर्घ्य का एकवर्णीय प्रकाश उपयोग करने पर, परदे के एक बिन्दु पर जहाँ पथान्तर λ है, प्रकाश की तीव्रता K इकाई है। उस बिन्दु पर प्रकाश की तीव्रता कितनी होगी जहाँ पथान्तर λ/3 है?
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q5

प्रश्न 6.
यंग के द्विझिर्स प्रयोग में व्यतिकरण फ्रिन्जों को प्राप्त करने के लिए 650 nm तथा 520 nm तरंगदैघ्र्यों के प्रकाश-पुंज का उपयोग किया गया।
(a) 650 nm तरंगदैर्घ्य के लिए परदे पर तीसरे दीप्त फ्रिन्ज की केन्द्रीय उच्चिष्ठ से दूरी ज्ञात कीजिए।
(b) केन्द्रीय उच्चिष्ठ से उस न्यूनतम दूरी को ज्ञात कीजिए जहाँ दोनों तरंगदैर्यों के कारण दीप्त फ्रिन्ज संपाती (coincide) होते हैं। (दिया है, D = 120 cm तथा d = 2 mm)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q6

प्रश्न 7.
एक द्विझिरी प्रयोग में एक मीटर दूर रखे परदे पर एक फ्रिन्ज की कोणीय चौड़ाई 0.2° पाई गई है। उपयोग किए गए प्रकाश की तरंगदैर्ध्य 600 nm है। यदि पूरा प्रायोगिक उपकरण जल में डुबो दिया जाए तो फ्रिन्ज की कोणीय चौड़ाई क्या होगी? जल का अपवर्तनांक $\frac { 4 }{ 3 }$ लीजिए।
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q7

प्रश्न 8.
वायु से काँच में संक्रमण (transition) के लिए बूस्टर कोण क्या है? (काँच का अपवर्तनांक = 1.5)।
हल-
बूस्टर के नियम से, n = tan i_p
बूस्टर कोण अर्थात् ध्रुवण कोण i_p = tan^-1 (n)
यहाँ n = 1.5 अतः i_p = tan^-1 (1.5) = 56.3°

प्रश्न 9.
5000 Å तरंगदैर्घ्य का प्रकाश एक समतल परावर्तक सतह पर आपतित होता है। परावर्तित प्रकाश की तरंगदैर्ध्य एवं आवृत्ति क्या है? आपतन कोण के किस मान के लिए परावर्तित किरण आपतित किरण के लम्बवत होगी?
हल-
यहाँ λ = 5000 Å = 5000 x 10^-10 मीटर = 5 x 10^-7
वायु में प्रकाश की चाले c = 3 x 10⁸ मी/से
वायु में प्रकाश की आवृत्ति
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q9
आपतित तथा परावर्तित किरण दोनों एक ही माध्यम (वायु) में होंगे।
अतः परावर्तित प्रकाश की तरंगदैर्घ्य = आपतित प्रकाश की तरंगदैर्घ्य = 5000 Å
परावर्तित प्रकाश की आवृत्ति = आपतित प्रकाश की आवृत्ति = 6 x 10¹⁴ हज
परावर्तन कोण r = आपतन कोण i
तथा परावर्तित किरण आपतित किरण के लम्बवत् है; अतः
i + r = 90°, i + i = 90°
वांछित आपतन कोण i = 45°

प्रश्न 10.
उस दूरी का आकलन कीजिए जिसके लिए किसी 4 mm के आकार के द्वारक तथा 400 nm तरंगदैर्घ्य के प्रकाश के लिए किरण प्रकाशिकी सन्निकट रूप से लागू होती है।
हल-
दिया है, λ = 400 nm = 400 x 10^-9 m, d = 4 x 10^-3 m
माना एकल झिरीं विवर्तन प्रतिरूप में प्रथम निम्निष्ठ केन्द्रीय उच्चिष्ठ से θ₁ कोण पर प्राप्त होता है, तब
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q10

अतिरिक्त अभ्यास

प्रश्न 11.
एक तारे में हाइड्रोजन से उत्सर्जित 6563 Å की H_α लाइन में 15 Å का अभिरक्त-विस्थापन (red-shift) होता है। पृथ्वी से दूर जा रहे तारे की चाल का आकलन कीजिए।
हल-
दिया है, λ = 6563 Å, अभिरक्त विस्थापन Δλ = 15 Å
तारे की चाल = ?
प्रकाश की चाल c = 3 x 10⁸ ms^-1
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q11

प्रश्न 12.
किसी माध्यम (जैसे जल) में प्रकाश की चाल निर्वात में प्रकाश की चाल से अधिक है। न्यूटन के कणिका सिद्धान्त द्वारा इस आशय की भविष्यवाणी कैसे की गई। क्या जल में प्रकाश की चाल प्रयोग द्वारा ज्ञात करके इस भविष्यवाणी की पुष्टि हुई? यदि नहीं, तो प्रकाश के चित्रण का कौन-सा विकल्प प्रयोगानुकूल है?
उत्तर-
न्यूटन के कणिका सिद्धान्त के अनुसार जब प्रकाश किसी विरल माध्यम से सघन माध्यम में प्रवेश करता है तो प्रकाश कणिकाओं पर, माध्यमों की सीमा पृष्ठ के अभिलम्बवत् दिशा में एक आकर्षण बल (विरल से सघने माध्यम की ओर) कार्य करने लगता है। इस बल के कारण कणिकाओं को, सीमा पृष्ठ के अभिलम्बवत् घटक बढ़ने लगता है, जबकि सीमा पृष्ठ के समान्तर घटक अपरिवर्तित रहता है। इससे प्रकाश किरण अभिलम्ब की ओर झुकती हुई सघन माध्यम में अपवर्तित हो जाती है।
सीमा पृष्ठ का समान्तर घटक अपरिवर्तित रहता है; अतः
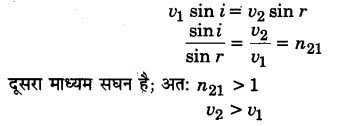
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q12
परन्तु प्रयोग द्वारा न्यूटन की इस भविष्यवाणी की पुष्टि नहीं हो पाई अपितु इसके विपरीत प्रयोग द्वारा यह ज्ञात हुआ कि सघन माध्यम में प्रकाश की चाल विरल माध्यम की तुलना में कम हाती है। इससे न्यूटन के कणिका सिद्धान्त को अमान्य करार दिया गया और हाइगेन्स के तरंगिका सिद्धान्त को मान्यता मिल गई। इससे ज्ञात होता है कि हाइगेन्स का तरंगिका सिद्धान्त प्रयोग संगत है।

प्रश्न 13.
आप मूल पाठ में जान चुके हैं कि हाइगेन्स का सिद्धान्त परावर्तन और अपवर्तन के नियमों के लिए किस प्रकार मार्गदर्शक है। इसी सिद्धान्त का उपयोग करके प्रत्यक्ष रीति से निगमन (deduce) कीजिए कि समतल दर्पण के सामने रखी किसी वस्तु का प्रतिबिम्ब आभासी बनता है, जिसकी दर्पण से दूरी, बिम्ब से दर्पण की दूरी के बराबर होती है।
उत्तर-
एक बिन्दु बिम्ब तथा एक समतल दर्पण लीजिए। बिन्दु बिम्ब को केन्द्र मानते हुए तथा दर्पण को स्पर्श करते हुए एक वृत्त खींचिए। यह बिम्ब से चलकर दर्पण तक पहुँचने वाले गोलीय तरंगाग्र का समतलीय भाग है। अब t समय पश्चात् दर्पण की उपस्थिति में तथा अनुपस्थिति में इस तरंगाग्र की स्थितियाँ आरेखित कीजिए। इस प्रकार दर्पण के दोनों ओर सर्वत्रसम चाप प्राप्त होंगे। इनमें से एक परावर्तित तरंगाग्र है। (पहचानिए)। सरल ज्यामिति के उपयोग से देखा जा सकता है कि परावर्तित तरंगाग्र का केन्द्र (बिम्ब को प्रतिबिम्ब) दर्पण से बिम्ब के बराबर दूरी पर है।

प्रश्न 14.
तरंग संचरण की चाल को प्रभावित कर सकने वाले कुछ सम्भावित कारकों की सूची है
(i) स्रोत की प्रकृति,
(ii) संचरण की दिशा,
(iii) स्रोत और / या प्रेक्षक की गति,
(iv) तरंगदैर्घ्य, तथा
(v) तरंग की तीव्रता।
बताइए कि …………
(a) निर्वात में प्रकाश की चाल,
(b) किसी माध्यम (माना काँच या जल) में प्रकाश की चाल इनमें से किन कारकों पर निर्भर करली है?
उत्तर-
(a) निर्वात् में प्रकाश की चाल एक सार्वत्रिक नियतांक है जो उपर्युक्त में से किसी भी कारक पर निर्भर नहीं करती। यहाँ तक कि स्रोत व प्रेक्षक के बीच आपेक्षिक गति पर भी नहीं। (b) किसी माध्यम में प्रकाश की चाल
(i) स्रोत की प्रकृति,
(ii) संचरण की दिशा,
(iii) स्रोत तथा माध्यम के बीच आपेक्षिक गति, तथा
(v) तरंग की तीव्रता पर निर्भर नहीं करती।
परन्तु यह
(iii) माध्यम तथा प्रेक्षक के बीच आपेक्षिक गति, तथा
(iv) प्रकाश की तरंगदैर्ध्य पर निर्भर करती है।

प्रश्न 15.
ध्वनि तरंगों में आवृत्ति विस्थापन के लिए डॉप्लर का सूत्र निम्नलिखित दो स्थितियों में थोड़ा-सा भिन्न है-
(i) स्रोत विरामावस्था में तथा प्रेक्षक गति में हो, तथा
(ii) स्रोत गति में परन्तु प्रेक्षक विरामावस्था में हो।
जबकि प्रकाश के लिए डॉप्लर के सूत्र निश्चित रूप से निर्वात में, इन दोनों स्थितियों में एकसमान हैं। ऐसा क्यों है? स्पष्ट कीजिए। क्या आप समझते हैं कि ये सूत्र किसी माध्यम में प्रकाश गमन के लिए भी दोनों स्थितियों में पूर्णतः एकसमान होंगे?
उत्तर-
निर्वात् में गतिमान प्रकाश के लिए डॉप्लर प्रभाव में प्रेक्षक द्वारा ग्रहण किए गए प्रकाश की आभासी आवृत्ति दोनों ही दशाओं में समान होती है। भले ही दर्शक, स्थिर स्रोत की ओर गति कर रहा हो अथवा स्रोत समान चाल से दर्शक की ओर गतिमान हो। इस प्रकार प्रकाश में डॉप्लर प्रभाव सममित है। दूसरी ओर ध्वनि तरंगों को चलने के लिए माध्यम की आवश्यकता होती है, इसलिए भले ही चाहे उक्त दोनों स्थितियों में प्रेक्षक तथा स्रोत के बीच समान आपेक्षिक गति होने के कारण ये स्थितियाँ समान प्रतीत होती हैं परन्तु वे समान नहीं हैं। ऐसा इस कारण से है कि दोनों दशाओं में प्रेक्षक का माध्यम के सापेक्ष वेग भिन्न-भिन्न है; अतः उक्त दोनों दशाओं में सुनी गई ध्वनि की आभासी आवृत्तियाँ समान नहीं हो सकतीं।

यदि किसी माध्यम में प्रकाश की गति की बात की जाए तो पुनः दोनों स्थितियाँ अलग-अलग हो जाएँगी चूंकि दोनों स्थितियों में प्रेक्षक का माध्यम के सापेक्ष वेग भिन्न-भिन्न होगा। अतः इस दशा में प्रेक्षक द्वारा ग्रहण किए गए प्रकाश की आवृत्ति के भिन्न डॉप्लर सूत्रों की अपेक्षा की जानी चाहिए।

प्रश्न 16.
द्विझिरी प्रयोग में, 600 nm तरंगदैर्घ्य का प्रकाश करने पर, एक दूरस्थ परदे पर बने फ्रिज की कोणीय चौड़ाई 0.1° है। दोनों झिर्रियों के बीच कितनी दूरी है?
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q16

प्रश्न 17.
निम्नलिखित प्रश्नों के उत्तर दीजिए।
(a) एकल झिरी विवर्तन प्रयोग में, झिरीं की चौड़ाई मूल चौड़ाई से दोगुनी कर दी गई है। यह केन्द्रीय विवर्तन बैंड के साइज तथा तीव्रता को कैसे प्रभावित करेगी?
(b) द्विझिरी प्रयोग में, प्रत्येक झिरी का विवर्तन, व्यतिकरण पैटर्न से किस प्रकार सम्बन्धित है?
(c) सुदूर स्रोत से आने वाले प्रकाश के मार्ग में जब एक लघु वृत्ताकार वस्तु रखी जाती है तो वस्तु की छाया के मध्य एक प्रदीप्त बिन्दु दिखाई देता है। स्पष्ट कीजिए क्यों?
(d) दो विद्यार्थी एक 10 m ऊँची कक्ष विभाजक दीवार द्वारा 7m के अन्तर पर हैं। यदि ध्वनि और प्रकाश दोनों प्रकार की तरंगें वस्तु के किनारों पर मुड़ सकती हैं तो फिर भी वे विद्यार्थी एक-दूसरे को देख नहीं पाते यद्यपि वे आपस में आसानी से वार्तालाप किस प्रकार कर पाते हैं?
(e) किरण प्रकाशिकी, प्रकाश के सीधी रेखा में गति करने की संकल्पना पर आधारित है। यद्यपि विवर्तन प्रभाव (जब प्रकाश का संचरण एक द्वारक/झिरी या वस्तु के चारों ओर प्रेक्षित किया जाए) इस संकल्पना को नकारता है तथापि किरण प्रकाशिकी की संकल्पना प्रकाशकीय यन्त्रों में प्रतिबिम्बों की स्थिति तथा उनके दूसरे अनेक गुणों को समझने के लिए सामान्यतः उपयोग में लाई जाती है। इसका क्या औचित्य है?
उत्तर-
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q17
अत: झिरीं की चौड़ाई दोगुनी करने पर, केन्द्रीय विवर्तन बैंड की चौड़ाई आधी रह जाएगी, जबकि तीव्रता चार गुनी (तीव्रता ∝ झिरीं का क्षेत्रफल) हो जाएगी।

(b) द्विझिरीं प्रयोग में व्यतिकरण पैटर्न की फ्रिन्ज एकल झिरीं विवर्तन पैटर्न की फ्रिन्जों के साथ अध्यारोपित होती हैं।

(c) वृत्तीय अवरोध के किनारों से विवर्तित तरंगें जब वस्तु की छाया के मध्य बिन्दु पर मिलती हैं तो वहाँ पथान्तर शून्य होने के कारण परस्पर संपोषी व्यतिकरण करती हैं; अत: वहाँ चमकदार बिन्दु दिखाई पड़ता है।

(d) दीवार की ऊँचाई 10 m, ध्वनि तरंगों की तरंगदैर्घ्य की कोटि की है; अत: यह ध्वनि तरंगों में पर्याप्त विवर्तन उत्पन्न करती है और एक विद्यार्थी की ध्वनि दीवार से विवर्तित होकर दूसरे विद्यार्थी तक पहुँच जाती है। वहीं प्रकाश की तरंगदैर्घ्य, दीवार की ऊँचाई की तुलना में अत्यन्त सूक्ष्म है; अत: दीवार प्रकाश तरंगों में पर्याप्त विवर्तन उत्पन्न नहीं कर पाती। इसी कारण विद्यार्थी एक-दूसरे को नहीं देख पाते।

(e) सामान्यतः प्रकाशिक यन्त्रों में प्रयुक्त लेन्सों के द्वारकों का साइज प्रकाश की तरंगदैर्ध्य की तुलना में काफी बड़ा होता है; अत: इन यन्त्रों द्वारा बने प्रतिबिम्बों में विवर्तन का प्रभाव नगण्य ही रहता है। यही कारण है कि प्रतिबिम्बों की स्थिति तथा अन्य गुणों को समझने के लिए प्रायः किरण प्रकाशिकी का ही प्रयोग किया जाता है।

प्रश्न 18.
दो पहाड़ियों की चोटी पर दो मीनारें एक-दूसरे से 40 km की दूरी पर हैं। इनको जोड़ने वाली रेखा मध्य में आने वाली किसी पहाड़ी के 50 m ऊपर से होकर गुजरती है। उन रेडियो तरंगों की अधिकतम तरंगदैर्घ्य ज्ञात कीजिए, जो मीनारों के मध्य बिना पर्याप्त विवर्तन प्रभाव के भेजी जा सकें?
हल-
फ्रेजनल दूरी तय करने पर ही तरंग प्रभाव ज्यामितीय प्रभाव पर हावी हो जाता है। अत: फ्रेजनल दूरी
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q18

प्रश्न 19.
500 pm तरंगदैर्ध्य का एक समान्तर प्रकाश-पुंज एक पतली झिरीं पर गिरता है तथा 1 m दूर परदे पर परिणामी विवर्तन पैटर्न देखा जाता है। यह देखा गया कि पहला निम्निष्ठ परदे पर केन्द्र से 2.5 mm दूरी पर है। झिरीं की चौड़ाई ज्ञात कीजिए।
हल-
विवर्तन प्रारूप में निम्निष्ठों के लिए e sin θ = mλ …(1)
प्रथम कोटि के निम्निष्ठों के लिए m = 1 तथा विवर्तन कोण 8 के छोटे मानों के लिए
sin θ = tan θ ~ θ = $\frac { x }{ D }$
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q19

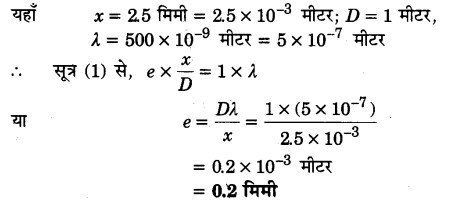
प्रश्न 20.
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) जब कम ऊँचाई पर उड़ने वाला वायुयान ऊपर से गुजरता है तो हम कभी-कभी टेलीविजन के परदे पर चित्र को हिलते हुए पाते हैं। एक सम्भावित स्पष्टीकरण सुझाइए।
(b) जैसा कि आप मूल पाठ में जान चुके हैं कि विवर्तन तथा व्यतिकरण पैटर्न में तीव्रता का वितरण समझने का आधारभूत सिद्धान्त तरंगों का रेखीय प्रत्यारोपण है। इस सिद्धान्त की तर्कसंगति क्या है?
उत्तर-
(a) ऐसा टेलीविजन के एन्टीना तक सीधे पहुंचने वाले तथा हवाई जहाज से टकराकर एन्टीना तक पहुँचने वाले संकेतों के बीच होने वाले व्यतिकरण के कारण होता है।

(b) तरंग गति को नियन्त्रित करने वाले अवकल समीकरण का चरित्र रेखीय होता है। यदि y₁ तथा y₂ ऐसे किसी समीकरण के दो अलग-अलग हल हैं तो y₁ + y₂ भी इस समीकरण का एक हल होगा (रेखीय अवकल समीकरण का गुण)। यही गुण तरंगों के रेखीय प्रत्यारोपण को तर्कसंगत ठहराता है।

प्रश्न 21.
एकल झिरी विवर्तन पैटर्न की व्युत्पत्ति में कथित है कि $\frac { n\lambda }{ a }$ कोणों पर तीव्रता शून्य है। इस निरसन (cancillation) को, झिरीं को उपयुक्त भागों में बाँटकर सत्यापित कीजिए।
हल-
माना e चौड़ाई की एकल झिरीं n छोटी झिर्रियों में बाँटी गयी है। अत: प्रत्येक झिर्रा की चौड़ाई
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics Q21
अतः n झिर्रियों में से प्रत्येक θ कोण की दिशा में शून्य तीव्रता प्रेरित करती है जिनमें प्रत्येक की चौड़ाई e’ है। अतः परिणामस्वरूप n झिर्रियों की तीव्रताओं का परिणामी भी शून्य ही होगा।

परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न

प्रश्न 1.
हाइगेन्स के अनुसार, प्रकाश की तरंगें होती हैं|
(i) यान्त्रिक, अनुदैर्घ्य
(ii) यान्त्रिक, अनुप्रस्थ
(iii) विद्युत, चुम्बकीय
(iv) यान्त्रिक, गोलीय
उत्तर-
(i) यान्त्रिक, अनुदैर्घ्य

प्रश्न 2.
वायु में प्रकाश की चाल 3.0 x 10⁸ मीटर/सेकण्ड है। 1.5 अपवर्तनांक वाले काँच में प्रकाश की चाल होगी- (2012)
(i) 1.5 x 10⁸ मीटर/सेकण्ड
(ii) 2.0 x 10⁸ मीटर/सेकण्ड
(iii) 1.0 x 10⁸ मीटर/सेकण्ड
(iv) 2.5 x 10⁸ मीटर/सेकण्ड
उत्तर-
(ii) 2.0 x 10⁸ मीटर/सेकण्ड

प्रश्न 3.
वायु में 4000 Å तरंगदैर्घ्य के एकवर्णी प्रकाश की किरणें जल (जिसका अपवर्तनांक = 4/3 है) में प्रवेश करती हैं। जल में इनकी तरंगदैर्ध्य होगी- (2011)
(i) 2500 Å
(ii) 3000 Å
(iii) 4000 Å
(iv) 5333 Å
उत्तर-
(ii) 3000 Å

प्रश्न 4.
जल की सतह पर तेल की पतली परत बिछी हुई है। सूर्य के प्रकाश में इस सतह पर सुन्दर रंग दिखाई देने का कारण है- (2013)
(i) प्रकाश का वर्णं विक्षेपण
(ii) प्रकाश का ध्रुवण,
(iii) प्रकाश का व्यतिकरण
(iv) प्रकाश का विवर्तन
उत्तर-
(iii) प्रकाश का व्यतिकरण

प्रश्न 5.
व्यतिकरण की घटना का कारण है|
(i) कलान्तर
(ii) आयाम परिवर्तन
(iii) वेग परिवर्तन
(iv) तीव्रता
उत्तर-
(i) कलान्तर

प्रश्न 6.
यदि व्यतिकरण करने वाली दो तरंगों की तीव्रताओं का अनुपात 16 : 9 है, तो व्यतिकरण प्रारूप में महत्तम एवं न्यूनतम तीव्रताओं को अनुपात है- (2010, 13)
(i) 4 : 3
(ii) 49 : 1
(iii) 25 : 7
(iv) 256 : 81
उत्तर-
(ii) 49 : 1

प्रश्न 7.
समान आयाम व समान तरंगदैर्ध्य की दो प्रकाश तरंगें अध्यारोपित की जाती हैं। परिणामी तरंग का आयाम अधिकतम होगा जब उनके बीच कलान्तर है- (2015)
(i) शून्य
(ii) $\frac { \pi }{ 4 }$
(iii) $\frac { \pi }{ 2 }$
(iv) π
उत्तर-
(i) शून्य

प्रश्न 8.
प्रकाश-तरंगों का किसी अवरोध की ज्यामितीय छाया में मुड़ना कहलाता है-
(i) प्रकाश का व्यतिकरण
(ii) विवर्तन
(iii) ध्रुवंण
(iv) वर्ण-विक्षेपण
उत्तर-
(ii) विवर्तन

प्रश्न 9.
प्रकाश सरल रेखा में चलता प्रतीत होता है, क्योंकि-
(i) सह वायुमण्डल द्वारा अवशोषित नहीं होता है।
(ii) इसकी चाल बहुत अधिक है।
(iii) इसकी तरंगदैर्ध्य बहुत छोटी है।
(iv) यह वायुमण्डल के ऊपरी भाग से परावर्तित हो जाता है।
उत्तर-
(iii) इसकी तरंगदैर्घ्य बहुत छोटी है।

प्रश्न 10.
एक एकल स्लिट, जिसकी चौड़ाई e है, तरंगदैर्घ्य λ के प्रकाश द्वारा प्रकाशित की जाती है। प्रथम निम्निष्ठ 60° के विवर्तन कोण पर प्राप्त होगा। यदि
(i) e = $\frac { \lambda }{ \surd 3 }$
(ii) e = $\frac { 2\lambda }{ \surd 3 }$
(iii) e = $\frac { 4\lambda }{ \surd 3 }$
(iv) e = $\frac { \sqrt { 3 } \lambda }{ 2 }$
उत्तर-
(ii) e = $\frac { 2\lambda }{ \surd 3 }$

प्रश्न 11.
वह घटना जो प्रकाश की अनुप्रस्थ तरंग प्रकृति दर्शाती है, है- (2010, 12)
(i) व्यतिकरण
(ii) विवर्तन
(iii) ध्रुवण
(iv) अपवर्तन
उत्तर-
(iii) ध्रुवण

प्रश्न 12.
सम्बन्ध n = tan i_p, कहलाता है-
(i) परावर्तन
(ii) व्यतिकरण
(iii) बूस्टर का नियम
(iv) न्यूटन का नियम
उत्तर-
(iii) बूस्टर का नियम

प्रश्न 13.
अपवर्तनांक n वाले पृष्ठ पर आपतित प्रकाश के लिए ध्रुवण कोण (बूस्टर कोण) होगा- (2013)
(i) sin^-1 (n)
(ii) tan^-1 (n)
(ii) cos^-1 (n)
(iv) tan^– ( $\frac { 1 }{ n }$ )
उत्तर-
(ii) tan^-1 (n)

प्रश्न 14.
ध्रुवण कोण (p) तथा क्रान्तिक कोण (C) में सम्बन्ध व्यक्त होता है- (2017)
(i) tan p = cosec C
(ii) tan p = sin C
(iii) tan p = sec C
(iv) tan p = cos C
उत्तर-
(i) tan p = cosec C

प्रश्न 15.
एक पोलेराइड की पारदर्शी प्लेट उसी प्रकार की एक अन्य प्लेट पर इस प्रकार रखी है कि इनकी ध्रुवण दिशाओं के बीच 30° का कोण बनता है। प्लेटों के इस युग्म में से एक पर । अधूवित प्रकाश आपतित होता है। निर्गत प्रकाश तथा आपतित अधूवित प्रकाश की तीव्रताओं का अनुपात होगा- (2017)
(i) 1 : 4
(ii) 1 : 3
(iii) 3 : 4
(iv) 3 : 8
उत्तर-
(ii) 1 : 3

प्रश्न 16.
प्रकाश तरंगों की अनुप्रस्थ प्रकृति की पुष्टि होती है- (2017)
(i) ध्रुवण के द्वारा
(ii) विवर्तन के द्वारा
iii) व्यतिकरण के द्वारा
(iv) आवर्तन के द्वारा
उत्तर-
(i) ध्रुवण के द्वारा

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
तरंगाग्र के लम्बवत् रेखा किसकी दिशा को प्रदर्शित करती है?
उत्तर-
तरंग-संचरण की दिशा को।

प्रश्न 2.
ऐसी दो भौतिक घटनाओं का उल्लेख कीजिए जो प्रकाश की तरंग प्रकृति की पुष्टि करती हैं।
उत्तर-
व्यतिकरण तथा विवर्तन।

प्रश्न 3.
निर्वात में किसी प्रकाश की तरंगदैर्घ्य 4800 Å है, जल में तरंगदैर्घ्य की गणना कीजिए। जल का अपवर्तनांक $\frac { 4 }{ 3 }$ है। (2010)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics VSAQ 3

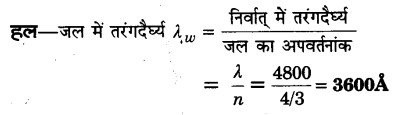
प्रश्न 4.
काँच-जल के मध्यपृष्ठ पर क्रान्तिक कोण ज्ञात कीजिए, यदि वायु के सापेक्ष काँच एवं जल के अपवर्तनांक क्रमशः $\frac { 3 }{ 2 }$ एवं $\frac { 4 }{ 3 }$ हैं। (2010)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics VSAQ 4

प्रश्न 5.
समान आवृत्ति वाली दो तरंगों के आयामों का अनुपात 5 : 3 है। इनके अध्यारोपण से उत्पन्न परिणामी तरंग की अधिकतम तथा न्यूनतम तीव्रताओं को अनुपात ज्ञात कीजिए। (2009, 11, 16)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics VSAQ 5

प्रश्न 6.
कला-सम्बद्ध स्रोतों से आप क्या समझते हैं? (2010)
उत्तर-
ऐसे दो स्रोतों को जिनके बीच कलान्तर सदैव नियत रहता है, कला-सम्बद्ध स्रोत (coherent sources) कहते हैं। दो कला-सम्बद्ध स्रोतों से हम स्थायी (sustained) व्यतिकरण प्रतिरूप प्राप्त कर सकते हैं। ऐसे स्रोत किसी युक्ति द्वारा एक ही स्रोत से प्राप्त किये जाते हैं।

प्रश्न 7.
यंग के व्यतिकरण प्रयोग में यदि दो प्रकाश-स्रोतों में से एक के मार्ग में काँच की पतली प्लेट रख दी जाए, तो फ्रिन्ज की चौड़ाई पर क्या प्रभाव पड़ेगा?
उत्तर-
कोई प्रभाव नहीं पड़ेगा, बल्कि व्यतिकरण प्रारूप उसी स्लिट की दिशा में विस्थापित हो जाएगा।

प्रश्न 8.
ध्वनि के व्यतिकरण पर आधारित दो यन्त्रों के नाम लिखिए। (2009)
उत्तर-
क्विण्के की नली, स्वरित्र द्विभुज।

प्रश्न 9.
प्रकाश के व्यतिकरण का एक प्राकृतिक तथा एक प्रायोगिक उदाहरण बताइए। (2009)
उत्तर-
तेल की परत का रंगीन दिखायी देना, यंग का प्रयोग।

प्रश्न 10.
अध्यारोपण का सिद्धान्त लिखिए। (2009)
उत्तर-
किसी माध्यम में दो अथवा दो से अधिक प्रगामी तरंगें एक साथ परन्तु एक-दूसरे की गति को बिना प्रभावित किये चल सकती हैं। अत: माध्यम के प्रत्येक कण का किसी क्षण परिणामी विस्थापन दोनों तरंगों द्वारा अलग-अलग उत्पन्न विस्थापनों के सदिश (vector) योग के बराबर होता है। इस सिद्धान्त को ‘अध्यारोपण का सिद्धान्त’ कहते हैं।

प्रश्न 11.
तरंगों के अध्यारोपण से कितने प्रकार के प्रभाव प्राप्त होते हैं? कौन-कौन से? (2009)
उत्तर-
तरंगों के अध्यारोपण से तीन प्रकार के प्रभाव प्राप्त होते हैं-

व्यतिकरण,
विस्पन्द,
अप्रगामी तरंगें।

प्रश्न 12.
यदि समान आयाम a की दो प्रकाश तरंगों के व्यतिकरण से परिणामी तरंग का आयाम a ही प्राप्त हो तब दोनों तरंगों के मध्य कलान्तर क्या होगा? (2016)
हल-
दोनों तरंगों के मध्य कलान्तर 120° होगा।

प्रश्न 13.
समान आवृत्ति की दो प्रकाश तरंगों के आयाम 4 : 3 के अनुपात में हैं। यदि दोनों तरंगें व्यतिकरण करें तो महत्तम व न्यूनतम तीव्रताओं का अनुपात क्या होगा? (2017)
हल-
दिया है, आयामों का अनुपाते, a₁ : a₂ = 4 : 3
अधिकतम तीव्रता के स्थान पर आयाम = (a₁ + a₂)
न्यूनतम तीव्रता के स्थान पर आयाम = (a₁ ~ a₂)
सूत्र I ∝ a² से,
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics VSAQ 13

प्रश्न 14.
दो प्रकाश तरंगों की तीव्रताओं का अनुपात 81 : 49 है। उनके आयामों का क्या अनुपात होगा? (2017)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics VSAQ 14

प्रश्न 15.
यदि स्लिट की चौड़ाई कम कर दी जाए तो केन्द्रीय उच्चिष्ठ की चौड़ाई पर क्या प्रभाव पड़ेगा ?
उत्तर-
कोणीय चौड़ाई = 2λ/d अर्थात् यह रेखा-छिद्र की चौड़ाई d के व्युत्क्रमानुपाती है। इसलिए स्लिट की चौड़ाई कम करने से केन्द्रीय उच्चिष्ठ की चौड़ाई बढ़ जाएगी।

प्रश्न 16.
एकल रेखा-छिद्र से प्राप्त विवर्तन प्रारूप में निम्निष्ठों की स्थिति के लिए सूत्र लिखिए तथा प्रयुक्त संकेतों के अर्थ स्पष्ट कीजिए। (2009)
उत्तर-
θ = ± mλ/e.
जहाँ, θ = कोणीय स्थिति, m कोई पूर्णांक,
λ = तरंगदैर्घ्य,
e = स्लिटों के बीच की दूरी।

प्रश्न 17.
किसी 1 x 10-5 मी की चौड़ाई वाली झिरीं पर 6000 Å तरंगदैर्घ्य का प्रकाश लम्बवत् पड़ रहा है। विवर्तन प्रारूप के केन्द्रीय उच्चिष्ठ की.कोणीय चौड़ाई की गणना कीजिए।
हल-
केन्द्रीय उच्चिष्ठ की कोणीय चौड़ाई
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics VSAQ 17

प्रश्न 18.
0.2 मिमी चौड़ाई वाले रेखाछिद्र से 2 मीटर दूर रखे पर्दे पर विवर्तन प्राप्त होता है। पर्दे पर केन्द्रीय उच्चिष्ठ के दोनों ओर 5 मिमी पर प्रथम निम्निष्ठ पाया जाता है। प्रकाश की तरंगदैर्ध्य की गणना कीजिए। (2011, 17)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics VSAQ 18

प्रश्न 19.
एकल स्लिट द्वारा विवर्तन में द्वितीय निम्निष्ठ 6.0 के विवर्तन में कोण पर प्राप्त होता है। यदि प्रकाश की तरंगदैर्घ्य λ हो तब स्लिट की चौड़ाई क्या होगी? (2015)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics VSAQ 19

प्रश्न 20.
ध्रुवण-कोण से क्या तात्पर्य है? (2012)
या
ध्रुवर्ण-कोण से आप क्या समझते हैं? (2014)
या
ध्रुवण-कोण क्या है? (2017)
उत्तर-
पारदर्शी माध्यम पर आपतित प्रकाश का वह आपतन कोण जिसके लिए परावर्तित प्रकाश पूर्णतया समतल ध्रुवित होता है, धुवण-कोण कहलाता है। इसको i_p से प्रदर्शित करते हैं।

प्रश्न 21.
एक पोलेराइड पर समतल-धुवित प्रकाश, पोलेराइड की ध्रुवण दिशा में (i) 45° के कोण पर, (ii) 60° के कोण पर गिरता है। पोलेराइड से निर्गत प्रकाश की तीव्रता, आपतित प्रकाश की तीव्रता की कितने प्रतिशत होगी? (2009)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics VSAQ 21

प्रश्न 22.
प्रकाश के ध्रुवण से प्रकाश की प्रकृति के किस तथ्य की पुष्टि होती है ? (2011)
उत्तर-
प्रकाश के ध्रुवण से प्रकाश के तरंग रूप की अनुप्रस्थ प्रकृति की पुष्टि होती है।

प्रश्न 23.
द्विवर्णता क्या है?
उत्तर-
टूरमैलीन क्रिस्टल द्वारा द्वि-अपवर्तन की घटना में इस क्रिस्टल द्वारा दो ध्रुवित अपवर्तित किरणों में से एक किरण को क्रिस्टल द्वारा अवशोषित करने का गुण द्विवर्णता कहलाता है।

प्रश्न 24.
ध्रुवित प्रकाश में कम्पन:-तल तथा ध्रुवण-तल के मध्य का कोण कितना होता है? (2009)
उत्तर-
90°

प्रश्न 25.
द्वि-अपवर्तन से आप क्या समझते हैं? (2011, 16)
उत्तर-
द्वि-अपवर्तन (Double Refraction)- टूरमैलीन, कैलसाइट, क्वार्ट्ज जैसे कुछ क्रिस्टल ऐसे होते हैं कि जब उन पर साधारण प्रकाश (अधुवित प्रकाश) की कोई किरण डाली जाती है, तो वह क्रिस्टल में प्रवेश करने पर दो अपवर्तित किरणों में बँट जाती है। इस घटना को द्वि-अपवर्तन कहते हैं। इन दो। अपवर्तित किरणों में से जो एक किरण अपवर्तन के नियमों का पालन करती है, साधारण किरण (ordinary ray) कहलाती है तथा दूसरी किरण जो अपवर्तन के नियमों का पालन नहीं करती, असाधारण किरण (extra-ordinary ray) कहलाती है। ये दोनों किरणें परस्पर लम्बवत् तलों में समतल ध्रुवित होती हैं।

प्रश्न 26.
√3 अपवर्तनांक वाले माध्यम के लिए ध्रुवण-कोण कितना होता है? (2012, 14)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics VSAQ 26

प्रश्न 27.
एक पारदर्शी माध्यम पर आपतित प्रकाश परावर्तन के बाद पूर्णतः समतल ध्रुवित पाया जाता है। माध्यम के लिए ध्रुवण कोण 45° है। माध्यम का अपवर्तनांक तथा अपवर्तन कोण का मान ज्ञात कीजिए। (2011)
हल-
ध्रुवण कोण हो, i_p = 45°
माध्यम का अपवर्तनांक n = tan i_p = tan 45° = 1
i_p + r = 90
अपवर्तन कोण r = 90° – i_p = 90° – 45° = 45°

प्रश्न 28.
उने दो भौतिक घटनाओं का उल्लेख कीजिए जिनसे प्रकाश के तरंग प्रकृति की पुष्टि होती- (2011, 17)
उत्तर-
व्यतिकरण तथा ध्रुवण।

लघु उत्तरीय प्रश्न

प्रश्न 1.
प्रिज्म द्वारा किसी समतल तरंगाग्र के परावर्तन तथा अपवर्तन को समझाइए।
उत्तर-
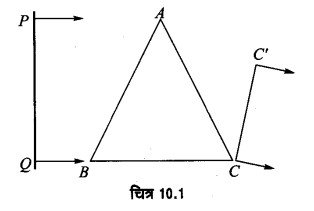
माना एक समतल तरंगाग्र PQ अल्प अपवर्तन कोण के प्रिज्म ABC पर आपतित होता है। हाइगेन्स के सिद्धान्तानुसार, तरंगाग्र PQ का प्रत्येक बिन्दु एक नये विक्षोभ केन्द्र की तरह कार्य करता है। ये विक्षोभ केन्द्र द्वितीयक तरंगिकाएँ उत्पन्न करते हैं। भिन्न-भिन्न द्वितीयक तरंगिकाएँ भिन्न-भिन्न मोटाइयों से होकर गुजरती हैं। Q से द्वितीयक तरंगिका C तक पहुँचने में प्रिज्म की सम्पूर्ण लम्बाई तय करेगी। दूसरी ओर प्रिज्म के बिन्दु A पर आपतन कोण के बाद P से द्वितीयक तरंगिका वायु में लगभग सम्पूर्ण दूरी तय करेगी। यह तरंगिका प्रिज्म में बहुत ही अल्प दूरी तय करने के पश्चात् बाहर निर्गत् होती है और पुन: वायु में गति करती है।

जिस समय तरंगिका प्रिज्म में B से C तक गति करती है। ठीक उसी समय P से तरंगिका वायु में लगभग सम्पूर्ण दूरी तय करने के पश्चात् C’ बिन्दु तक पहुँचती है और C’ भी उसी कला में होता है। परिणामस्वरूप एक समतल तरंगाग्र CC’ प्राप्त होता है जिसे निर्गत् समतल तरंगाग्र कहा जाता है। इस प्रकार हम निष्कर्ष निकालते हैं कि प्रिज्म से कोई समतल तरंगाग्रं एक समतल तंरंगाग्र के रूप में ही बाहर निकलता है।
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 1

प्रश्न 2.
प्रकाश के व्यतिकरण से क्या तात्पर्य है? इसके लिए आवश्यक प्रतिबन्ध क्या हैं? (2009, 11, 12, 13, 14, 15, 16)
या
दो प्रकाश पुंजों द्वारा बनी व्यर्तिकरण फ्रिन्जों को प्राप्त करने के लिये आवश्यक प्रतिबन्धों का उल्लेख कीजिए। (2010, 12)
या
प्रकाश के व्यतिकरण के लिए आवश्यक शर्ते बताइए। (2016)
उत्तर-
समान आवृत्ति की दो प्रकाश-तरंगें जिनके आयाम समान हों, जब किसी माध्यम में एक साथ चलती हैं तो माध्यम के विभिन्न बिन्दुओं पर प्रकाश की तीव्रता उने तरंगों की अलग-अलग तीव्रताओं के योग से भिन्न होती है। कुछ स्थानों पर प्रकाश की तीव्रता न्यूनतम (लगभग शून्य) होती है, जबकि कुछ स्थानों पर प्रकाश की तीव्रता अधिकतम होती है। प्रकाश-तरंगों की इस घटना को प्रकाश का व्यतिकरण कहते हैं। जिन स्थानों पर तीव्रता न्यूनतम होती है, उन स्थानों पर हुए व्यतिकरण को ‘विनाशी-व्यतिकरण’ तथा जिन स्थानों पर तीव्रता अधिकतम होती है, उन स्थानों पर हुए व्यतिकरण को संपोषी व्यतिकरण’, कहते हैं।
प्रकाश के व्यतिकरण के लिए आवश्यक शर्ते प्रकाश के व्यतिकरण के लिए आवश्यक शर्ते निम्नलिखित हैं|

दोनों प्रकाश-स्रोत ‘कला सम्बद्ध’ होने चाहिए, अर्थात् दोनों स्रोतों से प्राप्त तरंगों के बीच कलान्तर समय के साथ स्थिर रहना चाहिए।
दोनों तरंगों की आवृत्तियाँ (अथवा तरंगदैर्घ्य) बराबर होनी चाहिए।
दोनों तरंगों के आयाम बराबर होने चाहिए।
प्रकाश के दोनों स्रोतों के बीच दूरी बहुत कम होनी चाहिए जिससे दोनों तरंगाग्र एक ही दिशा में चलें और फ्रिजें अधिक चौड़ी बने।
दोनों प्रकाश-स्रोत बहुत संकीर्ण होने चाहिए।

प्रश्न 3.
तरंगों के संपोषी तथा विनाशी व्यतिकरण के लिए आवश्यक शर्ते बताइए। (2010, 13)
उत्तर-
संपोषी व्यतिकरण के लिए आवश्यक शर्ते
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 3
अतः संपोषी व्यतिकरण के लिए आवश्यक है, कि
(i) दोनों तरंगों के बीच कलान्तर शून्य अथवा π का सम गुणक होना चाहिए, अर्थात् तरंगें एक ही कला में मिलनी चाहिए।
(ii) दोनों तरंगों के बीच पथान्तर शून्य अथवा तरंगदैर्घ्य λ का पूर्ण गुणक होना चाहिए।

विनाशी व्यतिकरण के लिए आवश्यक शर्ते
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 3.1
अत: विनाशी व्यतिकरण के लिए आवश्यक है, कि
(i) दोनों तरंगों के बीच कलान्तर π का विषम गुणक होना चाहिए, अर्थात् तरंगें विपरीत कला में मिलनी चाहिए।
(ii) दोनों तरंगों के बीच पथान्तर अर्द्ध-तरंगदैर्घ्य (λ/2) का विषम गुणक होना चाहिए।

प्रश्न 4.
यंग के द्विक रेखा छिद्र प्रयोग में स्लिटें 0.28 mm दूरी पर हैं और पर्दा 1.4 मीटर दूर रखा है। केन्द्रीय दीप्त-फ्रिज और चौथी दीप्त फ्रिज के बीच की दूरी 1.2 सेमी है। प्रयोग में प्रयुक्त प्रकाश की तरंगदैर्ध्य एवं दीप्त फ्रिन्ज की चौड़ाई ज्ञात कीजिए। (2015)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 4

प्रश्न 5.
समान आवृत्ति की दो तरंगें जिनकी तीव्रताएँ I₀ तथा 9I₀ हैं, अध्यारोपित की जाती हैं। यदि किसी बिन्दु पर परिणामी तीव्रता 7I₀ हो तो उस बिन्दु पर तरंगों के बीच न्यूनतम कलान्तंर ज्ञात कीजिए।
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 5

प्रश्न 6.
यंग के प्रयोग में प्रीला प्रकाश तरंगदैर्घ्य 6000 Å, प्रयुक्त होने पर दृष्टि क्षेत्र में 60 फ्रिजें दिखाई देती हैं। यदि नीला प्रकाश जिसका तरंगदैर्घ्य 4500 Å है, प्रयोग में लाया जाये, तो कितनी फ्रिजें दिखाई देंगी ? (2012)
हल-
पीला प्रकाश (λ = 6000 Å) प्रयुक्त करने पर 60 फ्रिजें दिखाई पड़ती हैं; अतः
दृष्टि-क्षेत्र का विस्तार = फ्रिन्जों की संख्या x फ्रिन्ज की चौड़ाई
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 6

प्रश्न 7.
यंग के प्रयोग में दो स्लिटों के बीच की दूरी 2 x 10^-4 मीटर है। 6 x 10^-7 मीटर तरंगदैर्घ्य के प्रकाश द्वारा व्यतिकरण फ्रिजें 80.0 सेमी दूर पर्दे पर बनती हैं। केन्द्रीय फ्रिन्जे से द्वितीय दीप्त फ्रिन्ज की दूरी ज्ञात कीजिए। (2013)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 7

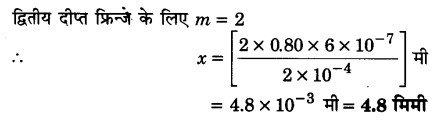
प्रश्न 8.
यंग केद्वि-स्लिट प्रयोग में स्लिटों के बीच की दूरी 10^-3 मीटर, स्लिटों तथा पर्दे के बीच की दूरी 3.0 मीटर तथा फ्रिज चौड़ाई 2.1 x 10^-3 मीटर पायी गयी। प्रयोग में प्रयुक्त प्रकाश का तरंगदैर्घ्य ज्ञात कीजिए।
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 8

प्रश्न 9.
दो झिर्रियों के बीच की दूरी 3 मिलीमीटर है। इस पर 6000 Å तरंगदैर्ध्य का प्रकाश लम्बवत् आपतित हो रहा है। 1 मीटर दूर पर्दे पर व्यतिकरण प्रारूप प्राप्त हो रहा है। फ्रिन्जों की चौडाई और केन्द्रीय फ्रिज से दूसरी अदीप्त फ्रिज की दूरी की गणना कीजिए।
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 9

प्रश्न 10.
यंग के द्विक रेखा छिद्र प्रयोग में 6600 Å तरंगदैर्ध्य का प्रकाश पर्दे पर व्यतिकरण प्रतिरूप प्राप्त करने के लिए प्रयुक्त है। फ्रिज की चौड़ाई 1.5 मिमी परिवर्तित हो जाती है जब पर्दा 50 सेमी द्विक रेखा छिद्र की ओर लाया जाता है। दोनों द्विक रेखा छिद्रों के बीच की दूरी ज्ञात कीजिए। (2016)
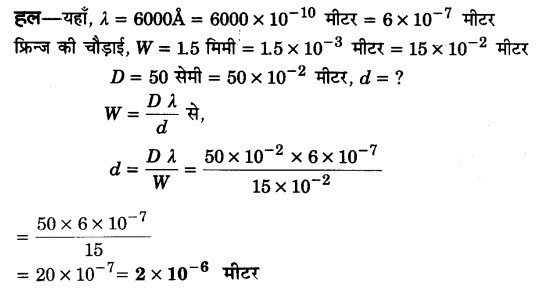
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 10

प्रश्न 11.
यंग के प्रयोग में दो स्लिटों के बीच की दूरी 0.4 मिमी है। प्रयुक्त प्रकाश की तरंगदैर्घ्य 6000 Å है। व्यतिकरण प्रारूप 100 सेमी दूर रखे पर्दे पर देखा जाता है। केन्द्रीय फ्रिज से द्वितीय अदीप्त एवं तृतीय दीप्त फ्रिज की दूरी की गणना कीजिए। (2017)
हल-
यदि स्लिटों के बीच की दूरी d, प्रकाश की तरंगदैर्घ्य λ तथा पर्दे की स्लिटों से दूरी D हो, तो केन्द्रीय फ्रिन्ज से m वीं अदीप्ते फ्रिन्ज की दूरी
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 11

प्रश्न 12.
यंग के द्वि-रेखाछिद्र प्रयोग में, स्लिटों के बीच की दूरी 0.2 मिमी और पर्दा 1.6 मी दूर है। यह देखा गया कि केन्द्रीय दीप्त फ्रिज और चौथी अदीप्त फ्रिज के बीच की दूरी 1.8 सेमी है। प्रयुक्त प्रकाश की तरंगदैर्ध्य की गणना कीजिए। (2017)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 12

प्रश्न 13.
यंग के द्वि-झिरी प्रयोग में स्लिटों के बीच दूरी 0.4 मिमी है। प्रयुक्त प्रकाश की तरंगदैर्घ्य 6000 Å है। 2 मीटर दूर रखे पर्दे पर प्राप्त व्यतिकरण प्रतिरूप में केन्द्रीय फ्रिन्ज से पाँचवें अदीप्त फ्रिन्ज की दूरी तथा फ्रिन्ज की चौड़ाई ज्ञात कीजिए। (2017)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 13

प्रश्न 14.
यंग के व्यतिकरण प्रयोग में 6000 Å तरंगदैर्घ्य के प्रकाश के लिए स्लिटों से एक मीटर की दूरी पर रखे पर्दे पर फ्रिन्ज की चौड़ाई 0.06 सेमी है। इसी स्थिति में यदि 5000 Å तरंगदैर्घ्य का प्रकाश प्रयोग में लाया जाये तो फ्रिन्जों की चौड़ाई कितनी होगी? (2014)
हल-
यदि स्लिटों के बीच अन्तराल d, स्लिटों से पर्दे की दूरी D तथा प्रकाश की तरंगदैर्घ्य λ हो तो फ्रिन्ज की चौड़ाई
W = $\frac { D\lambda }{ d }$
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 14

प्रश्न 15.
किसी 1 x 10^-5 मीटर चौड़ाई वाली झिरीं पर 6000 Å तरंगदैर्घ्य का प्रकाश लम्बवत् पड़ रहा है। विवर्तन प्रारूप के केन्द्रीय उच्चिष्ठ की कोणीय चौड़ाई की गणना कीजिए। (2012)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 15

प्रश्न 16.
व्यतिकरण तथा विवर्तन में क्या अन्तर है? (2016, 17)
या
प्रकाश के व्यतिकरण तथा विवर्तन की घटनाओं में अन्तर के लिए किसी एक विशिष्टता का उल्लेख कीजिए। (2014)
उत्तर-
व्यतिकरण तथा विवर्तन में निम्न अन्तर हैं-
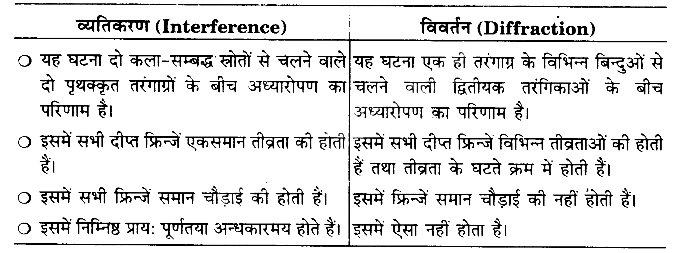
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 16

प्रश्न 17.
किसी 2 x 10^-5 मी चौड़ी स्लिट पर 5000 Å तरंगदैर्घ्य का प्रकाश अभिलम्बवत पड़ रही है। विवर्तन प्रारूप में प्रथम निम्निष्ठ, केन्द्रीय उच्चिष्ठ से कितनी कोणीय चौड़ाई पर स्थित होगा ? केन्द्रीय उच्चिष्ठ की कोणीय चौड़ाई भी ज्ञात कीजिए। (2010, 17)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 17

प्रश्न 18.
किसी 2 x 10^-5 मीटर चौड़ी स्लिट (झिरी) पर 5000 Å तरंगदैर्घ्य का प्रकाश अभिलम्बवत गिर रहा है। विवर्तन प्रतिरूप में केन्द्रीय उच्चिष्ठ की कोणीय चौड़ाई ज्ञात कीजिए। (2015)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 18

प्रश्न 19.
कम्पन-तल तथा ध्रुवण-तल की परिभाषा दीजिए। (2011)
या
ध्रुवण-तल की परिभाषा लिखिए। (2014)
उत्तर-
कम्पन-तल (Plane of Vibration)- समतल-ध्रुवित प्रकाश में उस तल को जिसमें प्रकाश के चलने की दिशा तथा वैद्युत वेक्टर के कम्पन की दिशा दोनों स्थित हों, ‘कम्पन-तल’ कहते हैं।
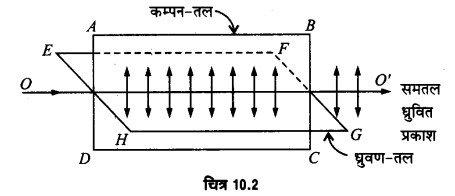
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 19
ध्रुवण-तल (Plane of Polarisation)- वह तल, जिसमें प्रकाश के चलने की दिशा स्थित हो तथा जो कम्पन-तल के अभिलम्बवत् हो ‘ध्रुवण-तल’ कहलाता है। इस तल में प्रकाश के कम्पन नहीं होते।

प्रश्न 20.
प्रकाश के ध्रुवण से आप क्या समझते हैं? समतल-धूवित प्रकाश उत्पन्न करने के लिए एक विधि का वर्णन कीजिए। (2009)
या
परावर्तन द्वारा आप समतल धुवित प्रकाश कैसे प्राप्त कर सकते हैं? (2012)
या
प्रकाश के ध्रुवण से आप क्या समझते हैं? (2014)
या
बूस्टर का नियम क्या है? किसी पारदर्शी माध्यम के लिए अपवर्तनांक एवं ध्रुवण कोण में सम्बन्ध लिखिए। (2016)
उत्तर-
प्रकाश का धुवण- प्रकाश की तरंगें अनुप्रस्थ तरंगें हैं जिनमें वैद्युत वेक्टर के कम्पन तरंग के संचरण की दिशा के लम्बवत् तल में सभी दिशाओं में होते हैं। टूरमैलीन क्रिस्टल में से गुजारने पर निर्गत् प्रकाश में वैद्युत वेक्टर के ये कम्पन संचरण की दिशा के लम्बवत् तल में केवल एक दिशा में रह जाते हैं, जबकि, शेष सभी कम्पन क्रिस्टल द्वारा अवशोषित कर लिये जाते हैं। क्रिस्टल से निर्गत् प्रकाश को ‘समतल-धुवित प्रकाश’ कहते हैं तथा यह घटना प्रकाश का धुवण’ कहलाती है।

परावर्तन द्वारा धूवित प्रकाश उत्पन्न करना- जब साधारण अथवा अध्रुवित प्रकाश किसी पारदर्शी माध्यम (जैसे–कॉच) के पृष्ठ से परावर्तित होता है तो वह आंशिक रूप से समतल ध्रुवित हो जाता है। परावर्तित प्रकाश में ध्रुवित प्रकाश की मात्रा, आपतन कोण पर निर्भर करती है। एक विशेष आपतन कोण in के लिए परावर्तित प्रकाश पूर्णतया समतल ध्रुवित होता है तथा इसके कम्पन आपतन तल के लम्बवत् होते हैं। इस आपतन कोण को ‘ध्रुवण-कोण’ (angle of polarization) कहते हैं। ध्रुवण-कोण पर परावर्तित एवं अपवर्तित किरणें परस्पर लम्बवत् होती हैं। परावर्तक माध्यम के अपवर्तनांक (n) और ध्रुवण-कोण (i_p) में निम्नलिखित सम्बन्ध होता है-
n = tan i_p
(यह सम्बन्ध बूस्टर का नियम कहलाता है।)
वायु-काँच के लिए कोण i_p का मान 57° होता है।

प्रश्न 21.
किसी पारदर्शी माध्यम का ध्रुवण-कोण 60° है। ज्ञात कीजिए
(i) माध्यम का अपवर्तनांक,
(ii) अपवर्तन कोण। [दिया गया है, tan 60° = √3] (2009, 17)
या
किसी पारदर्शी माध्यम के लिए ध्रुवण कोण 60° है। माध्यम के अपवर्तनांक की गणना कीजिए। (2015, 18)
हल-
(i) बूस्टर के नियम से अपवर्तनांक n = tan ip
n = tan 60° = √3 =1.782
(ii) i_p + r = 90°
अतः अपवर्तन कोण r = 90° – i_p
r = 90° – 60° = 30°

प्रश्न 22.
किसी माध्यम के लिए ध्रुवण-कोण 60° है। इसके लिए क्रान्तिक कोण कितना होगा?
या
एक पारदर्शी माध्यम का ध्रुवण कोण 60° है। माध्यम का अपवर्तनांक ज्ञात कीजिए। (tan 60° = √3) (2013)
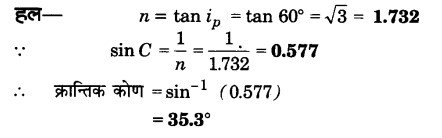
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 22

प्रश्न 23.
बूस्टर का नियम क्या है? दिखाइए कि जब प्रकाश, माध्यम पर ध्रुवण-कोण पर आपतित होता है, तो परावर्तित तथा अपवर्तित किरणें परस्पर लम्बवत होती हैं। (2009, 10, 11, 17)
या
ध्रुवण में बूस्टर के नियम का उल्लेख कीजिए। (2017)
या
ध्रुवण-कोण पर आपतित प्रकाश किरण की परावर्ती एवं अपवर्ती किरणों के मध्य कोण का मान ज्ञात कीजिए। (2012)
या
सिद्ध कीजिए कि ध्रुवण-कोण पर किसी किरण के आपतित होने पर परावर्तित एवं अपवर्तित किरणें परस्पर लम्बवत होती हैं। (2014, 17)
उत्तर-
बूस्टर का नियम-किसी पारदर्शी माध्यम के अपवर्तनांक (n) तथा ध्रुवण (i_p) के बीच सम्बन्ध n = tan i_p है। इसे बूस्टर का नियम कहते हैं।
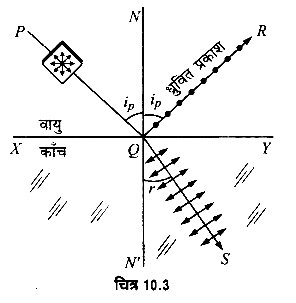
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 23

प्रश्न 24.
क्षितिज के ऊपर सूर्य का प्रकाश किस कोण पर आपतित हो जिससे शान्त जल के तल से परावर्तित प्रकाश पूर्णतः समतल ध्रुवित हो? (जल का अपवर्तनांक 1.327 तथा tan 53° = 1.327) (2014, 17)
हल-
माना सूर्य के क्षैतिज के ऊपर θ कोण पर होने पर जल के तल से परावर्तित प्रकाश पूर्णतः ध्रुवित है। इस स्थिति में, सूर्य से आपतित प्रकाश का जल के तल पर आपतन कोण MON = ध्रुवण कोण i_p होगा। परावर्तित प्रकाश पूर्णत: समतल-ध्रुवित होने की दशा में,
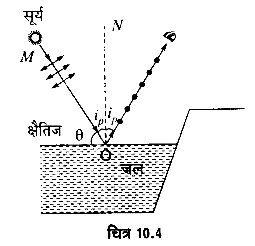
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics SAQ 24
बूस्टर के नियम से, अपवर्तनांक n = tan i_p,
अथवा 1.327 = tan i_p = tan 53°
अतः आपतन कोण i_p = 53°
क्षैतिज से कोण θ = 90° – 53° = 37°

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
तरंगाग्र किसे कहते हैं? हाइगेन्स के द्वितीयक तरंगिकाओं का सिद्धान्त लिखिए। (2009, 11, 12, 13, 18)
या
हाइगेन्स के तरंग संचरण सम्बन्धी सिद्धान्त की व्याख्या कीजिए। (2009, 17)
या
तरंगाग्र किसे कहते हैं? (2014, 18)
या
हाइगेन्स के द्वितीयक तरंगिकाओं के सिद्धान्त की विवेचना कीजिए। (2016, 17, 18)
उत्तर-
तरंगाग्र (Wavefront)- किसी एक माध्यम में जिसमें कोई तरंग संचरित हो रही हो, यदि हम कोई ऐसा पृष्ठ (surface) खींचें जिसमें स्थित कण कम्पन की समान कला में हों, तो ऐसे पृष्ठ को ‘तरंगाग्र कहते हैं। समांग (isotropic) माध्यम में किसी तरंग का तरंगाग्र सदैव तरंग संचरण की दिशा के लम्बवत् होता है। अत: तरंगाग्र के लम्बवत् खींची गयी रेखा तरंग के चलने की दिशा को व्यक्त करती है। इसको ही किरण (ray) कहते हैं। तरंगाग्र विविध आकृतियों के होते हैं।

हाइगेन्स का द्वितीयक तरंगिकाओं का सिद्धान्त (Huygens Principle of Secondary Wavelets)
1. जब कोई कम्पन-स्रोत तरंगें उत्पन्न करता है, तो उसके चारों ओर माध्यम (ईथर) के कण कम्पन करने लगते हैं। माध्यम को वह पृष्ठ (surface) जिसमें स्थित सभी कण एक ही कला (phase) में कम्पन कर रहे होते हैं, “तरंगाग्र’ (wavefront) कहलाता है। समांग (homogeneous) माध्यम में किसी तरंग का तरंगाग्र, तरंग के संचरण की दिशा में लम्बवत् होता है। अत: तरंगाग्र के अभिलम्बवत् खींची गयी रेखा तरंग के संचरण की दिशा को व्यक्त करती है तथा इसे किरण (ray) कहते हैं।

2. माध्यम में जहाँ भी तरंगाग्र पहुँचता है वहाँ पर स्थित प्रत्येक कण एक नया तरंग स्रोत बन जाता है। जिसमें नयी तरंगें सभी दिशाओं में निकलती हैं। इन तरंगों को द्वितीयक तरंगिकाएँ (secondary wavelets) कहते हैं। द्वितीयक तरंगिकाएँ प्राथमिक तरंग की चाल से ही आगे बढ़ती हैं।

3. किसी क्षण सभी द्वितीयक तरंगिकाओं को स्पर्श करता हुआ खींचा गया पृष्ठ अर्थात् ‘एन्वलोप’ (envelope) उस क्षण तरंगाग्र की नवीन स्थिति को प्रदर्शित करता है। इस प्रकार तरंग आगे बढ़ती चली जाती है।
चित्र 10.5 (a) में S एक बिन्दु स्रोत है जिससे तरंगें निकल रही हैं। माना कि तरंगों की चाल v है। माना कि किसी क्षण तरंगाग्र की स्थिति AB है।
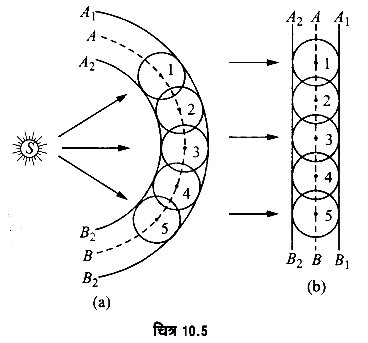
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 1
AB पर स्थित प्रत्येक बिन्दु से द्वितीयक गोलीय तरंग प्राथमिक तरंग की चाल से चारों ओर फैल रही है। माना कि हमें । समय उपरान्त तरंगाग्र की स्थिति ज्ञात करनी है। इतने समय में प्रत्येक द्वितीयक तरंगिका ut दूरी तय करेगी। अत: हम AB पर स्थित बिन्दुओं; जैसे 1, 2, 3, 4, 5,…… पर vt त्रिज्या के गोले खींचते हैं। इन गोलों को स्पर्श करता हुआ खींचा गया पृष्ठ A₁B₁ ‘एन्वलोप है। यही तरंगाग्र की नवीन स्थिति है। गोलों का एन्वलोप A₂B₂ पीछे की दिशा में भी है, परन्तु हाइगेन्स का सिद्धान्त पीछे की दिशा में स्थित ‘एन्वलोप’ को स्वीकार नहीं करता। ठीक इसी प्रकार चित्र 10.5 (b) में समतले तरंगाग्र का बढ़ना समझाया गया है।

प्रश्न 2.
हाइगेन्स के द्वितीयक तरंगिकाओं के सिद्धान्त की सहायता से तरंगों के अपवर्तन की व्याख्या कीजिए तथा स्नैल के नियम का निगमन कीजिए। (2011)
या
हाइगेन्स तरंग सिद्धान्त के आधार पर प्रकाश तरंगों के अपवर्तन की व्याख्या कीजिए। (2013, 18)
या
हाइगेन्स के द्वितीयक तरंगिकाओं के सिद्धान्त के आधार पर प्रकाश तरंगों के अपवर्तन के नियम की व्याख्या कीजिए। (2014, 18)
उत्तर-
जब कोई तरंग एक समांग माध्यम में चलकर किसी दूसरे समांग माध्यम में प्रवेश करती है तो वह अपने मार्ग से विचलित हो जाती है। इस घटना को अपवर्तन कहते हैं। इसमें तरंग की आवृत्ति नहीं बदलती परन्तु तरंग की चाल एवं तरंगदैर्घ्य बदल जाती हैं।

चित्र 10.6 में ZZ’ समतल पृष्ठ है जो दो माध्यमों को अलग करता है। माना इन माध्यमों में किसी तरंग की चालें क्रमशः v1 व v2 हैं। माना पहले माध्यम में एक समतल तरंगाग्र AB तिरछा आपतित होता है। और पहले माध्यम में पृष्ठ ZZ’ के बिन्दु A को t = 0 समय पर स्पर्श करता है तथा तरंगाग्र के बिन्दु B को A’ तक पहुँचने में है समय लगता है, तब BA’ = v1t
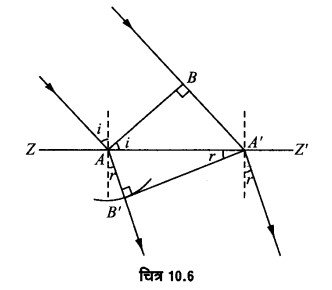
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 2
तरंगाग्र AB के आगे बढ़ने पर वह सीमा पृष्ठ के A व A’ के बीच के बिन्दुओं से टकराता है। इन बिन्दुओं से हाइगेन्स की गोलीय तरंगिकाएँ निकलने लगती हैं जो पहले माध्यम में v₁ चाल से और दूसरे माध्यम में v₂ चाल से चलने लगती हैं। सर्वप्रथम A से चलने वाली द्वितीयक तरंगिका । समय में दूसरे माध्यम में AB’ (= v₂t) दूरी तय करती है और इतने ही समय में बिन्दु B, पहले माध्यम में BA’ (= v₁t) दूरी चलकर A’ पर पहुँच जाता है जहाँ से अब द्वितीयक तरंगिका चलना प्रारम्भ करती है। इस प्रकार
AB’ = v₂t , BA’ = v₁t

बिन्दु A को केन्द्र मानकर AB’ त्रिज्या का एक चाप खींचते हैं तथा A’ से इस चाप पर स्पर्श रेखा A B’ खींचते हैं। जैसे-जैसे आपतित तरंगाग्रे AB आगे बढ़ता जाता है, A व A’ के बीच सभी बिन्दुओं से एक के बाद एक चलने वाली द्वितीयक तरंगिकाएँ एक साथ A’B’ को स्पर्श करेंगी; अर्थात् A’B’ सभी द्वितीयक तरंगिकाएँ को स्पर्श करेगा। अत: A’B’ ‘अपवर्तित’ तरंगाग्र होगा। माना कि आपतित तरंगाग्र AB तथा अपवर्तित तरंगाग्र A’B’ अपवर्तक तल ZZ’ के साथ क्रमश: कोण तथा r बनाते हैं। अब समकोण त्रिभुज ABA’ में
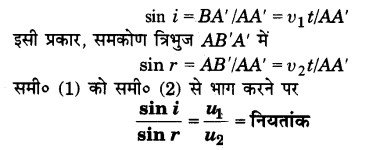
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 2.1
यही अपवर्तन का प्रथम नियम है। इसको ही स्नैल का नियम कहते हैं। चित्र 10.6 से स्पष्ट है कि आपतित किरण, अपवर्तित किरण तथा आपतन बिन्दु पर अभिलम्ब एक ही तल में हैं (यही अपवर्तन का दूसरा नियम है।)

स्नैल के नियम में प्रयुक्त नियतांक को दूसरे माध्यम का (पहले माध्यम के सापेक्ष) अपवर्तनांक कहते हैं तथा इसे ‘ ${ _{ 1 }{ n }_{ 2 } }$ ‘ से प्रदर्शित करते हैं।
अतः
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 2.2

प्रश्न 3.
हाइगेन्स के द्वितीयक तरंगिकाओं के सिद्धान्त के आधार पर परावर्तन के नियमों की व्याख्या कीजिए। (2012, 14)
या
हाइगेन्स के द्वितीयक तरंगिकाओं के सिद्धान्त के आधार पर प्रकाश के परावर्तन की व्याख्या कीजिए। (2017)
उत्तर-
हाइगेन्स के द्वितीयक तरंगिकाओं के सिद्धान्त के आधार पर प्रकाश के परावर्तन के नियमों की व्याख्या- चित्र 10.7 में ZZ’ एक परावर्तक पृष्ठ है। जिस पर ABएक समतल तरंगाग्र कोण i के झुकाव पर आपतित है। माना कि है = 0समय पर तरंगाग्र, पृष्ठ ZZ’ को बिन्दु A पर स्पर्श करता है। माना कि तरंगाग्र की चाल v है तथा तरंगाग्र, के बिन्दु B को पृष्ठ के बिन्दु A तक पहुँचने में है समय लगता है। जैसे-जैसे तरंगाग्र AB आगे बढ़ता है, वह परावर्तक पृष्ठ के A व A’ के बीच के बिन्दुओं से टकराता जाता है। हाइगेन्स के सिद्धान्त के अनुसार, A व A’ के बीच स्थित ये सभी बिन्दु नये तरंग स्रोतों का कार्य करते हैं। इनमें नई गोलीय तरंगिकाएँ सभी दिशाओं में निकलती हैं जो चाल के माध्यम से फैलती हैं। सबसे पहले बिन्दु A से द्वितीयक तरंगिका चलती है जो t समय में AB’ (= vt) दूरी तय करती है। परन्तु इसी समय में तरंगाग्र का बिन्दु B, दूरी BA’ चलकर A’ को स्पर्श कर लेता है, यहाँ से भी अब द्वितीयक तरंगिका चलनी शुरू हो जाती है। उपर्युक्त से स्पष्ट है कि
AB’ = BA’ = vt ……(1)
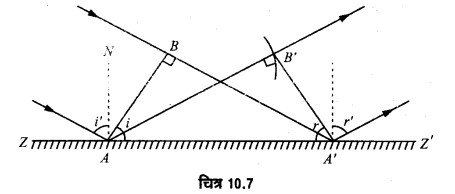
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 3
बिन्दु A को केन्द्र मानते हुए AB’ त्रिज्या का एक गोलीय चाप खींचते हैं तथा A’ से इस चाप पर स्पर्श रेखा (tangent) A’B’ खींच लेते हैं। जैसे-जैसे आपतित तरंगाग्र AB आगे बढ़ता है, परावर्तक पृष्ठ के A व A’ के बीच स्थित सभी बिन्दुओं से एक के बाद एक चलने वाली द्वितीयक तरंगिकाएँ भी एक साथ A’B’ को स्पर्श करेंगी, अथवा A’B’ सभी द्वितीयक तरंगिकाओं को स्पर्श करती है। हाइगेन्स के अनुसार यह A’B’ ही परावर्तित तरंगाग्र है। माना कि यह पृष्ठ ZZ’ से r कोण के झुकाव पर है। अब समकोण त्रिभुज ABA’ तथा A’B’A में भुजा AA’ उभयनिष्ठ है तथा BA = AB’; अत: दोनों त्रिभुज सर्वांगसम (congruent) हैं, इसलिए कोण BAA’ = कोण B’A’ A.

स्पष्ट है कि आपतित तरंगाग्र AB तथा परावर्तित तरंगाग्र A’ B’ परावर्तक पृष्ठ ZZ’ से बराबर कोण बनाते हैं। चूँकि तरंगाग्र के अभिलम्बवत् खींची गई रेखा किरण होती है, अतः आपतित तथा परावर्तित किरणे पृष्ठ ZZ’ खींचे गये अभिलम्ब से भी बराबर कोण बनाती हैं। अतः
आपतन कोण i = परावर्तन कोण r (यह परावर्तन का दूसरा नियम है।)
चूँकि AB, A’B’ व ZZ’ कागज के तेल में हैं। इन पर खींचे गये अभिलम्ब भी एक तल में होंगे। इस प्रकार आपतित किरण, परावर्तित किरण तथा आपतन बिन्दु पर अभिलम्ब तीनों एक ही तल में है। यही परावर्तन का प्रथम नियम है।

प्रश्न 4.
यंग के व्यतिकरण प्रयोग में दो समान्तर स्लिटों के बीच की दूरी d तथा उनसे पर्दे की दूरी D है। यदि प्रकाश की तरंगदैर्घ्य λ हो, तो पर्दे पर केन्द्रीय फ्रिज से किसी
(i) दीप्त फ्रिज,
(ii) अदीप्त फ्रिन्ज की दूरी के लिए व्यंजक स्थापित कीजिए।
या
यंग के व्यतिकरण प्रयोग में दो समान्तर स्लिटों के बीच की दूरीd तथा उनसे पर्दे की दूरी D है। यदि प्रकाश की तरंगदैर्घ्य λ हो तो पर्दे पर केन्द्रीय फ्रिन्ज से किसी दीप्त फ्रिज की दूरी के लिए व्यंजक स्थापित कीजिए। इससे फ्रिन्ज की चौड़ाई के लिए सूत्र W = $\frac { D\lambda }{ d }$ ज्ञात कीजिए। (2014)
या
द्वि-झिरी प्रयोग में बनी दीप्त फ्रिन्जों की चौड़ाई के लिए व्यंजक का निगमन कीजिए। (2013)
या
यंग के द्विक स्लिट प्रयोग में दीप्त अथवा अदीप्त फ्रिन्जों की चौड़ाई w के लिए सूत्र W = $\frac { D\lambda }{ d }$ व्युत्पादित कीजिए। प्रयुक्त संकेतों के सामान्य अर्थ हैं। (2013)
या
यंग के दो स्लिटों के प्रयोग में दीप्त फ्रिन्ज की चौड़ाई के लिए व्यंजक W = $\frac { D\lambda }{ d }$ प्राप्त कीजिए, जहाँ प्रयुक्त संकेतों के अर्थ सामान्य हैं। (2009)
या
प्रकाश के व्यतिकरण के लिए यंग के प्रयोग का विवरण दीजिए। फ्रिन्जों की चौड़ाई के लिए सूत्र प्राप्त कीजिए। (2012, 14, 17)
या
दो पतली समान्तर झिरीं, जो एक-दूसरे से d दूरी पर स्थित हैं, λ तरंगदैर्घ्य के प्रकाश से प्रकाशित की जाती हैं तथा झिर्रियों से D दूरी पर स्थित पर्दे पर फ्रिन्ज बनाती हैं। फ्रिन्जों की चौड़ाई के लिए व्यंजक प्राप्त कीजिए। (2015)
या
व्यतिक्रण की शर्तों का उल्लेख कीजिए। यंग के द्वि-झिरीं प्रयोग बनाने वाली फ्रिन्जों की चौड़ाई के लिए W = $\frac { D\lambda }{ d }$ का निगमन कीजिए। जहाँ प्रयुक्त संकेतों का अर्थ सामान्य है। (2016)
या
यंग के द्वि-स्लिट प्रयोग में प्राप्त व्यतिकरण फ्रिन्जों की चौड़ाई हेतु व्यंजक प्राप्त कीजिए। (2017)
उत्तर-
व्यतिकरण के लिए आवश्यक शर्त- लघु उत्तरीय प्रश्न 2 को उत्तर देखें।
फ्रिन्जों की चौड़ाई के लिए सूत्र-चित्र 10.8 में, S एक रेखा-छिद्र है जिसे एकवर्णी प्रकाश से प्रकाशित किया जाता है। इस रेखा-छिद्र से आगे दो रेखा-छिद्र S₁ व S₂ हैं जो एक-दूसरे के बहुत समीप हैं, S के संमान्तर हैं तथा उससे समान दूरी पर स्थित हैं। S से चलने वाली द्वितीयक तरंगिकाएँ S₁ व S₂ पर समान कला में पहुँचती हैं। S₁ व S₂ भी द्वितीयक तरंगिकाओं के स्रोत बन जाते हैं। इससे निकली तरंगें एक-दूसरे के साथ अध्यारोपण के पश्चात् D दूरी पर स्थित पर्दे पर व्यतिकरण फ्रिजें बनाती हैं। इन फ्रिन्जों की चौड़ाई नापकर प्रकाश की तरंगदैर्ध्य की भी गणना की जा सकती है।
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 4

प्रश्न 5.
यंगके द्विक रेखाछिद्र (द्विझिरीं) के प्रयोग में 1.5 अपवर्तनांक वाली काँच की एक पतली प्लेट किसी एक स्लिट (झिरी) से आने वाली प्रकाश किरण के मार्ग में रख दी जाती है। केन्द्रीय दीप्त फ्रिन्ज हटकर चौथी दीप्त फ्रिन्ज की स्थिति में पहुँच जाती है। यदि प्रयुक्त प्रकाश की तरंगदैर्ध्य 6000 Å हो, तो प्लेट की मोटाई ज्ञात कीजिए। (2013)
हल-
माना केन्द्रीय फ्रिन्ज की चौड़ाई = W
स्लिटों के बीच की दूरी = d
तथा स्लिटों से पर्दे की दूरी = D
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 5

प्रश्न 6.
यंग के द्वि-स्लिट प्रयोग में दो तरंगदैर्यों 6500 Å तथा 5200 Å के प्रकाश पुंज का उपयोग करके व्यतिकरण फ्रिजें प्राप्त की जाती हैं।
(i) तरंगदैर्घ्य 5200 A के लिए पर्दे पर केन्द्रीय फ्रिन्ज (उच्चिष्ठ) से द्वितीय अदीप्त फ्रिज की दूरी ज्ञात कीजिए।
(ii) केन्द्रीय उच्चिष्ठ से वह न्यूनतम दूरी क्या है, जहाँ पर दोनों तरंगदैर्घ्य से उत्पन्न दीप्त फ्रिजें सम्पाती हों? स्लिटों के बीच की दूरी 2 मिमी तथा स्लिटों व पर्दे के बीच की दूरी 120 सेमी हैं। (2016)
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 6

प्रश्न 7.
कलमसम्बद्ध स्रोत से क्या तात्पर्य है? व्यतिकरण की शर्तों का उल्लेख कीजिए। प्रकाश के व्यतिकरण सम्बन्धी प्रयोग में दो स्लिटों के बीच अन्तराल 0.2 मिमी है। इनसे निर्गत प्रकाश के व्यतिकरण से 1 मीटर दूर पर्दे पर बनी व्यतिकरण फ्रिन्ज की चौड़ाई 3 मिमी है। स्लिटों पर आपतित प्रकाश के तरंगदैर्घ्य एवं केन्द्रीय दीप्त फ्रिन्ज से तृतीय अदीप्त फ्रिज की दूरी ज्ञात कीजिए। (2016)
हल-
ऐसे दो स्रोतों को जिनके बीच कलान्तर सदैव नियत रहता है, कलासम्बद्ध स्रोत (coherent source) कहते हैं। दो कलासम्बद्ध स्रोतों से हम स्थायी (sustained) व्यतिकरण प्रतिरूप प्राप्त कर सकते हैं। ऐसे स्रोत किसी युक्ति द्वारा एक ही स्रोत से प्राप्त किये जाते हैं।
प्रकाश के व्यतिकरण के लिए आवश्यक शर्ते- लघु उत्तरीय प्रश्न 2 का उत्तर देखें। दिया है, d = 0.2 मिमी = 2 x 10^-4 मी, D = 1 मी,
W = 3 मिमी = 3 x 10^-3 मी
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 7

प्रश्न 8.
प्रकाश के विवर्तन से आप क्या समझते हैं? एक पतली झिरी से प्रकाश के विवर्तन के कारण प्राप्त विवर्तन प्रारूप की व्याख्या कीजिए। (2010, 11, 16, 17)
या
एक पतली झिरी से होने वाले प्रकाश के विवर्तन की विवेचना विवर्तन प्रतिमान खींचकर कीजिए। (2011)
या
किसी पतली झिरी द्वारा एकवर्णी प्रकाश के विवर्तन की विवेचना कीजिए तथा केन्द्रीय उच्चिष्ठ की कोणीय चौड़ाई ज्ञात कीजिए। (2012, 13, 16, 17)
उत्तर-
प्रकाश का विवर्तन- जब प्रकाश किसी अवरोध (obstacle) या द्वारक (aperture) पर जिसका आकार प्रकाश के तरंगदैर्घ्य के क्रम का हो, आपतित होता है तो अवरोध या द्वारक के किनारों पर प्रकाश ऋजुरेखीय संचरण से विचलित होकर मुड़ जाता है। जिस स्थान पर ज्यामितीय छाया बननी चाहिए। थी वहाँ भी कुछ प्रकाश पहुँच जाता है। अवरोध या द्वारक के किनारों पर प्रकाश का यह मुड़ना प्रकाश का विवर्तन कहलाता है। प्रकाश का विवर्तन

निम्नलिखित दो घटनाओं से प्रदर्शित होता है-
(i) ज्यामितीय छाया में प्रकाश का पहुँचना।
(ii) एकसमान प्रदीप्त क्षेत्र में फ्रिन्जों का बनना।

एक पतली झिर्रा से प्रकाश का विवर्तन- चित्र 10.10 में S एक बिन्दुवत् एकवर्णी (monochromatic) प्रकाश-स्रोत है। यह लेन्स L के प्रथम फोकस पर रखा है। अत: S, से चली प्रकाश किरणेंलेन्स L से अपवर्तन के पश्चात् एक समान्तर किरण-पुंज के रूप में निकलेंगी। समानान्तर किरणों का यह किरण-पुंज एक समतल तरंगाग्र (wavefront) ww’ का निर्माण करता है। इस लेन्स L के सामने एक लम्बी संकीर्ण स्लिट AB रखी है जिस पर यह समतल तरंगाग्र लम्बवत् आपतित होता है। स्लिट की चौड़ाई से है। जैसे ही यह तरंगाग्र स्लिट पर आपतित होती है तो हाइगेन्स के तरंग संचरण सम्बन्धी द्वितीयक तरंगिकाओं के सिद्धान्तानुसार, तरंगाग्र का प्रत्येक बिन्दु नये तरंग उत्पादक स्रोत का कार्य करता है तथा इनसे द्वितीयक तरंगिकाएँ निकलने लगती हैं। इन विवर्तित किरणों को लेन्स L2 द्वारा पर्दे YY’ पर फोकस कर लिया जाता है। स्लिट से एक नियत कोण पर विवर्तित सभी किरणें पर्दे के एक बिन्दु पर फोकस होती हैं। इस प्रकार पर्दे पर विवर्तन प्रारूप (diffraction pattern) प्राप्त हो जाता है।

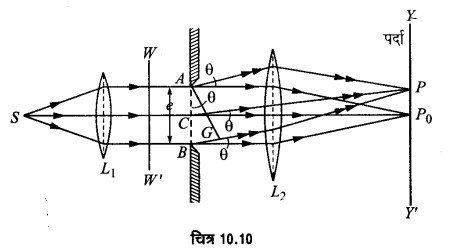
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 8
व्याख्या (Explanation)- जो तरंगिकाएँ θ = शून्य कोण पर विवर्तित होकर पर्दे के केन्द्रीय बिन्दु P, पर अध्यारोपित होती हैं वे सभी समान कला में होती हैं; अर्थात् उनके बीच कलान्तर शून्य होता है। इसलिए Py पर एक दीप्त फ्रिन्ज (बैण्ड) प्राप्त होता है। यह एक दीप्त चौड़ी पट्टी होती है। एक केन्द्रीय बैण्ड के दोनों ओर घटती हुई तीव्रता के अदीप्त व दीप्त बैण्ड एकान्तर क्रम में प्राप्त होते हैं। इस प्रकार पर्दे पर प्राप्त दीप्त व अदीप्त बैण्डों का यह प्रारूप विवर्तन प्रारूप कहलाता है। रेखा-छिद्र (slit) जितना कम चौड़ाई का होता है, उसका विवर्तन प्रारूप उतना ही अधिक फैला होता है तथा केन्द्रीय बैण्ड (पट्टी) उतना ही अधिक चौड़ा होता है।
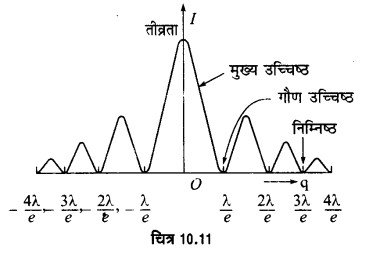
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 8.1
विवर्तन प्रारूप में PO पर बना दीप्त बैण्ड केन्द्रीय उच्चिष्ठ अथवा मुख्य उच्चिष्ठ (principal maxima) कहलाता है तथा इसके दोनों ओर घटती तीव्रता के दीप्तं बैण्ड गौण

गौण उच्चिष्ठ उच्चिष्ठ (secondary maxima) कहलाते हैं। दो क्रमागत दीप्त बैण्डों के बीच स्थित अदीप्त बैण्ड निम्निष्ठ (minima) कहलाते हैं। जो द्वितीयक तरंगिकाएँ रेखा-छिद्र AB पर है। कोण से विवर्तित होती हैं वे पर्दे YY’ पर केन्द्रीय बिन्दु PO से ऊपर बिन्दु P पर फोकस होती हैं। ये तरंगिकाएँ रेखा-छिद्र AB के विभिन्न भागों से एक ही कला में चलती हैं, परन्तु P पर भिन्न-भिन्न कलाओं में (पथान्तर के अनुसार) पहुँचकर परस्पर अध्यारोपित होती हैं। चित्र 10.10 में BG पर AG लम्ब डाला गया है। तल AG से पर्दे पर बिन्दु P एक प्रकाशीय पथ बराबर है। अतः रेखा-छिद्र के बिन्दु A तथा B से चलने वाली द्वितीयक तरंगिकाओं के बीच पथान्तर BG है। माना पथान्तर BG = λ जंहाँ λ प्रयुक्त प्रकाश की तरंगदैर्घ्य है। माना AB की चौड़ाई को n बराबर भागों में विभाजित कर लिया जाता है। प्रत्येक अर्द्ध-भाग के संगत बिन्दुओं से चलने वाली । तरंगिकाओं के बीच पथान्तर λ/2 होगा; अत: वे P पर अदीप्त बैण्ड उत्पन्न करेंगी। यह प्रथम निम्निष्ठ होगा जिसके लिए BG = λ.

परन्तु चित्र 10.10 से, BG = AB sin θ = e sin θ (जहाँ AB = e)
अत: P पर प्रथम निम्निष्ठ की स्थिति के लिए सूत्र e sin θ = λ.
अतः सभी निम्निष्ठों की स्थिति के लिए सामान्य सूत्र निम्नलिखित होगा-
e sin θ = ± mλ. (जहाँ m = 1, 2, 3…) …(1)
जबकि m = 0 मुख्य उच्चिष्ठ की स्थिति के संगत है।
यहाँ ± चिह्नों का अर्थ है कि निम्निष्ठ P पर बनने वाले मुख्य उच्चिष्ठ के दोनों ओर बनते हैं।
दो क्रमागत निम्निष्ठों के बीच भी कुछ प्रकाश पहुँच जाता है जहाँ कम चमकीले उँच्चिष्ठ प्राप्त होते हैं। इनको गौण उच्चिष्ठ (secondary maxima) कहते हैं। इनकी तीव्रता मुख्य उच्चिष्ठ के दोनों ओर चित्र 10.11 की भाँति तेजी से गिरती जाती है।
θ बहुत छोटा होने पर sin θ = θ …(2)
अतः उपर्युक्त समी० (1) से।
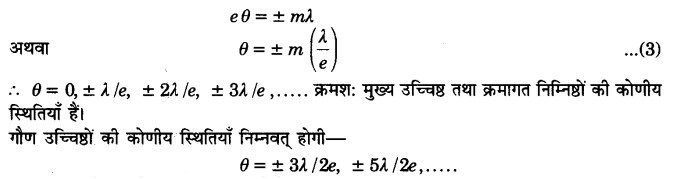
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 8.2
चित्र 10.11 में प्रदर्शित वक्र एकल पतले रेखा-छिद्र द्वारा प्राप्त विवर्तन प्रारूप का तीव्रता वितरण वक्र है। इसमें आपतित प्रकाश की तीव्रता का अधिकतम भाग केन्द्रीय उच्चिष्ठ में केन्द्रित होता है और शेष तीव्रता द्वितीयक उच्चिष्ठों में तेजी से घटते क्रम में पायी जाती है। उदाहरण के लिए, यदि केन्द्रीय उच्चिष्ठ की तीव्रता I₀ है तो द्वितीयक उच्चिष्ठों की तीव्रताएँ क्रमशः I₀/22, I₀/61,…… इत्यादि होती हैं।
केन्द्रीय उच्चिष्ठ की चौड़ाई के लिए व्यंजक
केन्द्रीय उच्चिष्ठ के दोनों ओर प्रथम निम्निष्ठों के बीच की कोणीय दूरी केन्द्रीय उच्चिष्ठ की चौड़ाई कहलाती है।
अतः केन्द्रीय उच्चिष्ठ की कोणीय चौड़ाई = θ + θ = 2θ = 2(λ/e)
यदि लेन्स L₂ की फोकस दूरी f हो जो रेखा-छिद्र AB के काफी समीप रखा हो, तो इससे दूरस्थ पर्दे पर केन्द्रीय उच्चिष्ठ की रैखिक चौड़ाई निम्न प्रकार ज्ञात की जाती है-
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 8.3

प्रश्न 9.
ध्रुवित तथा अधुवित प्रकाश में अन्तर समझाइए। (2012, 15)
उत्तर-
धुवित तथा अधुवित प्रकाश में अन्तर- साधारण प्रकाश में वैद्युत वेक्टर के कम्पन तरंग संचरण की दिशा के लम्बवत् सभी दिशाओं में होते हैं, अर्थात् ये तरंग संचरण की दिशा के परितः सममित होते हैं, अत: साधारण प्रकाश को अधुवित प्रकाश (unpolarised light) कहा जाता है। यदि किसी युक्ति द्वारा साधारण प्रकाश के वैद्युत वेक्टरों के कम्पन, तरंग संचरण की दिशा के लम्बवत् तल में केवल एक दिशा में सीमित कर दिये जायें, अर्थात् इन कम्पनों को तरंग संचरण की दिशा के परितः असममित कर दिया जाये तो इस प्रकार प्राप्त प्रकाश धुवित प्रकाश (polarised light) कहलाता है। इसी को समतल ध्रुवित प्रकाश भी कहते हैं। प्रकाश सम्बन्धी यह घटेंना प्रकाश का धुवण (polarisation of light) कहलाती है।

अधूवित प्रकाश में प्रकाश के संचरण की दिशा के लम्बवत् तल में कम्पन की सभी दिशाएँ सम्भव हैं, अतः अध्रुवित प्रकाश को एक तारे द्वारा प्रदर्शित किया जाता है [चित्र 10.12 (a)]।
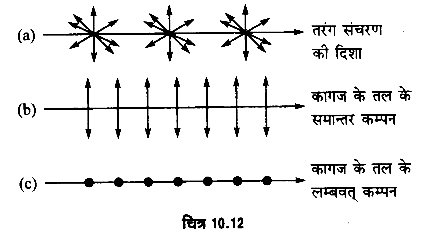
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 9
प्रकाश के समतल-ध्रुवित पूँज में कम्पन एक सीधी रेखा के अनुदिश होते हैं। जब कम्पन कागज के तल के समान्तर होते हैं, तो वे तीर युक्त रेखाओं द्वारा निरूपित किये जाते हैं [चित्र 10.12 (b)]। जब कम्पन कागज के तल के लम्बवत् एक सीधी रेखा के अनुदिश होते हैं, तो वे बिन्दुओं द्वारा निरूपित किये जाते हैं [चित्र 10.12 (c)]

प्रश्न 10.
पोलेराइड किसे कहते हैं? इसकी सहायता से कैसे पता लगायेंगे कि दिया गया प्रकाश अधुवित है, आंशिक रूप से धुवित है या पूर्णतः ध्रुवित है? (2015)
या
पोलेराइड से किसी प्रकाश किरण के धुवित होने की जाँच आप कैसे करेंगे?
या
पोलेराइड द्वारा समतल ध्रुवित प्रकाश के उत्पन्न करने तथा विश्लेषण करने की विधि का वर्णन कीजिए। (2010, 11)
या
समतल ध्रुवित प्रकाश के उत्पादन तथा संसूचन की किसी विधि का सचित्र वर्णन कीजिए। (2011)
या
पोलेराइड क्या है? इसकी कार्यविधि का वर्णन कीजिए। इसकी सहायता से अधुवित तथा समतल ध्रुवित प्रकाश में किस प्रकार अन्तर कर सकते हैं? (2013)
या
समतल ध्रुवित प्रकाश उत्पन्न करने हेतु किसी एक विधि का वर्णन कीजिए। (2015)
उत्तर-
पोलेराइड एक बड़े आकार की फिल्म होती है जिसे दो काँच की प्लेटों के बीच रखा जाता है। इस फिल्म को बनाने के लिए कार्बनिक यौगिक हरपेथाइट या आयोडो सल्फेट ऑफ क्यूनाइन के अतिसूक्ष्म क्रिस्टल, नाइट्रो-सेलुलोस की पतली चादर पर विशेष विधि द्वारा इस प्रकार फैला दिये जाते हैं कि सभी क्रिस्टलों की प्रकाशिक असें समान्तर रहें। ये क्रिस्टल द्विवर्णक होते हैं।

कार्यविधि- अधूवित प्रकाश में वैद्युत वेक्टर सभी दिशाओं में होते हैं। जब कोई प्रकाश किरण पोलेराइड फिल्म पर आपतित होती है, तो यह दो समतल ध्रुवित किरणों में विभक्त हो जाती है। एक किरण में वैद्युत वेक्टर हरपेथाइट क्रिस्टल की अक्ष के समान्तर तथा दूसरे में अक्ष के लम्बवत् होते हैं। इनमें से हरपेथाइट की अक्ष के लम्बवत् वैद्युत वेक्टर वाली किरण पूर्णतया अवशोषित हो जाती है। इस प्रकार निर्गत प्रकाश पूर्णतया ध्रुवित होता है। पोलेराइड से निर्गत प्रकाश समतल ध्रुवित होता है, इसकी जाँच एक-दूसरे पोलेराइड द्वारा संचरित हो जाता है [चित्र 10.13 (a)]। जब द्वितीय पोलेराइड को 90° से घुमाकर उसको क्रॉस स्थिति में लाते हैं, तो उनमें से प्रकाश संचरित नहीं होता [चित्र 10.13 (b)]। इस स्थिति में दोनों पोलेराइड की ध्रुवण दिशाएँ परस्पर लम्बवत् होती हैं। इस दशा में पोलेराइड क्रॉसित पोलेराइड हैं। उपर्युक्त प्रक्रिया में पहला (analyser) कहलाता है।
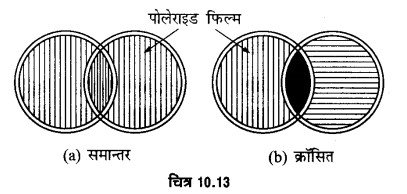
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 10
धूवित प्रकाश प्राप्त करना- जब ध्रुवित प्रकाश का एक किरण-पुंज पोलेराइड फिल्म में से गुजरता है, तो फिल्म केवल उन घटकों को पार होने देती है जिनके वैद्युत-वेक्टर पोलेराइड की ध्रुवण दिशा के समांन्तर कम्पन करते हैं। इस प्रकार पारगमित प्रकाश समतल-ध्रुवित प्रकाश होता है।
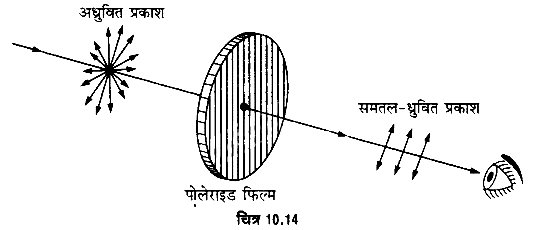
UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics LAQ 10.1
समतल-धुवित प्रकाश का संसूचन- पोलेराइड की सहायता से अधुवित, आंशिक रूप से ध्रुवित अथवा, पूर्णतया ध्रुवित प्रकाश का पता लगाया जाता है। किसी पोलेराइड को आपतित प्रकाश के परितः पूरा एक चक्कर घुमाने से यदि निर्गत प्रकाश की तीव्रता में कोई अन्तर नहीं पड़ता तो आपतित प्रकाश अधूवित है, निर्गत प्रकाश की तीव्रता में परिवर्तन तो होता है, परन्तु किसी भी स्थिति में तीव्रता शून्य नहीं होती तो आपतित प्रकाश आंशिक रूप से ध्रुवित है, यदि निर्गत प्रकाश की तीव्रता में परिवर्तन होता है। तथा पोलेराइड के एक चक्कर में दो बार तीव्रता अधिकतम तथा दो बार शून्य हो जाती है तो आपतित प्रकाश पूर्णत: समतल-ध्रुवित है।

We hope the UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics (तरंग-प्रकाशिकी) help you.

UP Board Solutions for Class 12 Physics Chapter 10 Wave Optics (तरंग-प्रकाशिकी)

Leave a Reply Cancel reply