UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance (स्थिरवैद्युत विभव तथा धारिता)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
5 x 10^-8 C तथा -3 x 10^-8 C के दो आवेश 16 cm दूरी पर स्थित हैं। दोनों आवेशों को मिलाने वाली रेखा के किस बिन्दु पर विद्युत विभव शून्य होगा? अनन्त पर विभव शून्य लीजिए।

UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q1.1

प्रश्न 2.
10 cm भुजा वाले एक सम-षट्भुज के प्रत्येक शीर्ष पर 5 µC का आवेश है। षट्भुज के केन्द्र पर विभव परिकलित कीजिए।
हल-
समषट्भुज के केन्द्र से प्रत्येक शीर्ष की दूरी समान होती है तथा यह इसकी भुजा a = 10 सेमी के बराबर होगी (चित्र 2.3)। चूंकि प्रत्येक शीर्ष पर आवेश भी समान (q = 5 µC = 5 x 10^-6 C) है, अत: प्रत्येक शीर्ष पर स्थित आवेश के कारण केन्द्र O पर विभव समान होगा।

प्रश्न 3.
6 cm की दूरी पर अवस्थित दो बिन्दुओं A एवं B पर दो आवेश 2 µC तथा -2 µC रखे है।
(a) निकाय के सम विभव पृष्ठ की पहचान कीजिए।
(b) इस पृष्ठ के प्रत्येक बिन्दु पर विद्युत-क्षेत्र की दिशा क्या है?
हल-
(a) दिया है, A व B पर दो आवेश 2 µC और -2 µC रखे हैं।
AB = 6 सेमी = 0.06 मीटर
दो दिए गए आवेशों के निकाय का समविभवी पृष्ठ A व B को मिलाने वाली रेखा के अभिलम्बवत् होगा। यह पृष्ठ, रेखा AB के मध्य बिन्दु C से गुजरेगा।
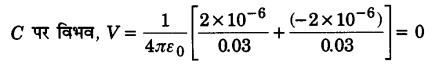
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q3
इस प्रकार इस पृष्ठ के प्रत्येक बिन्दु पर समान विभव है और यह शून्य है। अतः यह एक समविभवी पृष्ठ है।
(b) हमें ज्ञात है कि वैद्युत क्षेत्र सदैव + से – आवेश की ओर दिष्ट होता है। इस प्रकार यहाँ वैद्युत क्षेत्र (+ve) बिन्दु A से ऋणावेशित (-ve) बिन्दु B की ओर कार्य करता है। तथा यह समविभवी पृष्ठ के अभिलम्बवत् है।

प्रश्न 4.
12 cm त्रिज्या वाले एक गोलीय चालक के पृष्ठ पर 1.6 x 10^-7 C पर आवेश एकसमान रूप से वितरित है।
(a) गोले के अन्दर
(b) गोले के ठीक बाहर
(c) गोले के केन्द्र से 18 cm पर अवस्थित, किसी बिन्दु पर विद्युत-क्षेत्र क्या होगा?
हल-
आवेश सदैव चालक के पृष्ठ पर रहता है तथा बाहरी बिन्दुओं के लिए यह ऐसे व्यवहार करता है जैसे सम्पूर्ण आवेश इसके केन्द्र पर स्थित हो।
(a) गोले के भीतर वैद्युत क्षेत्र, E_in = 0
(b) गोले के पृष्ठ पर वैद्युत क्षेत्र

प्रश्न 5.
एक समान्तर पट्टिका संधारित्र, जिसकी पट्टिकाओं के बीच वायु है, की धारिता 8 pF (1 pF = 10^-12 F) है। यदि पट्टिकाओं के बीच की दूरी को आधा कर दिया जाए और इनके बीच के स्थान में 6 परावैद्युतक’का एक पदार्थ भर दिया जाए तो इसकी धारिता क्या होगी?
हल-
दिया है : पट्टिकाओं के बीच वायु होने पर समान्तर पट्ट संधारित्र की धारिता
C₀ = 8 pF = 8 x 10^-12 F
यदि प्रत्येक पट्टिका का क्षेत्रफल = A
तथा पट्टिकाओं के बीच दूरी = d हो, तो

प्रश्न 6.
9 pF धारिता वाले तीन संधारित्रों को श्रेणीक्रम में जोड़ा गया है।
(a) संयोजन की कुल धारिता क्या है?
(b) यदि संयोजन को 120 V के संभरण (सप्लाई) से जोड़ दिया जाए, तो प्रत्येक संधारित्र पर क्या विभवान्तर होगा?
हल-
तीनों संधारित्रों में प्रत्येक की धारिता 9 pF है।
अर्थात् C₁ = C₂ = C₃ = 9 pF; संभरण वोल्टता V = 120 वोल्ट
(a) यदि इनके श्रेणी संयोजन की कुल धारिता C_s हो

प्रश्न 7.
2 pF, 3 pF और 4 pF धारिता वाले तीन संधारित्र पाश्र्वक्रम में जोड़े गए हैं।
(a) संयोजन की कुल धारिता क्या है?
(b) यदि संयोजन को 100 V के संभरण से जोड़ दें तो प्रत्येक संधारित्र पर आवेश ज्ञात कीजिए।
हल-
यहाँ C₁ = 2 pF, C₂ = 3 pF, C₃ = 4 pF तथा संभरण वोल्टता V = 100 वोल्ट
(a) संधारित्रों के पाश्र्वक्रम (समान्तर संयोजन) की कुल धारिता
C = C₁ + C₂ + C₃ = 2 pF + 3 pF + 4 pF = 9 pF
(b) पाश्र्वक्रम संयोजन के प्रत्येक संधारित्र के सिरों के बीच वोल्टता संभरण वोल्टता के बराबर ही होगी अर्थात् V = 100 वोल्ट
अतः C₁ = 2 pF = 2 x 10^-12 F पर आवेश
Q₁ = C₂ x V = 2 x 10^-12 F x 100 वोल्ट = 2 x 10^-10 कूलॉम
C₂ = 3 pF = 3 x 10^-12 F पर आवेश
Q₂ = C₂ x V = 3 x 10^-12 F x 100 वोल्ट = 3 x 10^-10 कूलॉम
C₃ = 4 pF = 4 x 10^-12 F पर आवेश
Q₃ = C₃ x V = 4 x 10^-12 F x 100 वोल्ट = 4 x 10^-10 कूलॉम

प्रश्न 8.
पट्टिकाओं के बीच वायु वाले समान्तर पट्टिको संधारित्र की प्रत्येक पट्टिका का क्षेत्रफल 6 x 10^-3 m² तथा उनके बीच की दूरी 3 mm है। संधारित्र की धारिता को परिकलित कीजिए। यदि इस संधारित्र को 100 V के संभरण से जोड़ दिया जाए तो संधारित्र की प्रत्येक पट्टिका पर कितना आवेश होगा?
हल-
दिया है, प्लेट क्षेत्रफल A = 6 x 10^-3 m, y = 100 वोल्ट
बीच की दूरी d = 3 mm = 3 x 10^-3 m
धारिता C = ?, प्रत्येक पट्टी पर आवेश = ?

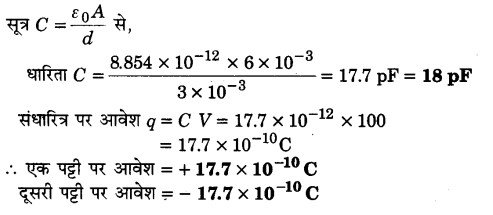
प्रश्न 9.
प्रश्न 8 में दिए गए संधारित्र की पट्टिकाओं के बीच यदि 3 mm मोटी अभ्रक की एक शीट (पत्तर) (परावैद्युतांक = 6) रख दी जाती है तो स्पष्ट कीजिए कि क्या होगा जब
(a) विभव (वोल्टेज) संभरण जुड़ा ही रहेगा।
(b) संभरण को हटा लिया जाएगा?
हल-
प्रश्न 8 के परिणाम से,
V = 100 वोल्ट,
q = 18 x 10^-10 C
अब माध्यम का परावैद्युतांक K = 6
परावैद्युत की मोटाई t = 3 mm = 3 x 10^-3 m
t = d; अत: संधारित्र पूर्णतः परावैद्युत द्वारा भरा है।
संधारित्र की नई धारिता C = KC₀ = 6 x 18 pF [C₀ = 18 pF]
= 108 pF
(a) विभव संभरण जुड़ा हुआ है; अत: संधारित्र का विभवान्तर नियत अर्थात् 100 वोल्ट रहेगा।
संधारित्र पर नया आवेश q = CV = 108 x 10^-12 x 100
= 1.08 x 10^-8 C
अतः इस स्थिति में, C = 108 pF, V = 100 V, q = 1.08 x 10^-8 C
(b) विभव संभरण हटा लिया गया है; अत: संधारित्र पर आवेश q = 18 x 10^-10 C नियत रहेगा।
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q9

प्रश्न 10.
12pF का एक संधारित्र 50 V की बैटरी से जुड़ा है। संधारित्र में कितनी स्थिर विद्युत ऊर्जा संचित होगी?
हल-
यहाँ C = 12 pF = 12 x 10^-12 फैरड; V = 50 वोल्ट
अत: स्थिर वैद्युत ऊर्जा
U = $\frac { 1 }{ 2 }$ CV²
= $\frac { 1 }{ 2 }$ x (12 x 10^-12) x (50)² जूल
= 1.50 x 10^-8 जूल

प्रश्न 11.
200 V संभरण (सप्लाई) से एक 600 pF से संधारित्र को आवेशित किया जाता है। फिर इसको संभरण से वियोजित कर देते हैं तथा एक अन्य 600 pF वाले अनावेशित संधारित्र से जोड़ देते हैं। इस प्रक्रिया में कितनी ऊर्जा का ह्रास होता है?
हल-
दिया है, धारिताएँ C₁ = 600 x 10^-12 F, C₂ = 600 x 10^-12 F
विभवान्तर V₁ = 200 V, V₂ = 0 V .
प्रक्रिया में ऊर्जा का हास ΔU = ?
आवेश के बाद संभरण को हटा दिया जाता है; अतः निकाय पर कुल’ आवेश नियत रहेगा।
माना संधारित्रों को जोड़ने पर उनका उभयनिष्ठ विभव V है,
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q11

अतिरिक्त अभ्यास

प्रश्न 12.
मूल बिन्दु पर एक 8 mC का आवेश अवस्थित है। -2 x 10^-9 के एक छोटे से आवेश को बिन्दु P(0, 0, 3 cm) से, बिन्दु R(0, 6 cm, 9 cm) से होकर, बिन्दु Q(0, 4 cm, 0) तक ले जाने में किया गया कार्य परिकलित कीजिए।

हल-
मूल बिन्दु पर आवेश Q = 8 x 10^-3 C
दूसरा आवेश q = -2 x 10^-9 C
स्थिरविद्युत क्षेत्र में किसी आवेश को एक बिन्दु से दूसरी बिन्दु तक ले जाने में किया जाने वाला कार्य मार्ग के स्थान पर अन्त्य बिन्दुओं पर निर्भर करता है।
आवेश q को बिन्दु P से Q तक ले जाने में किया गया कार्य
W = q (V_Q – V_P)
यहाँ बिन्दु Q की मूल बिन्दु से दूरी r_Q = OQ = 0.04 m
तथा बिन्दु P की मूल बिन्दु से दूरी r_P = OP = 0.03 m
मूल बिन्दु पर स्थित आवेश Q के कारण Q व P के बीच विभवान्तर

प्रश्न 13.
b भुजा वाले एक घन के प्रत्येक शीर्ष पर q आवेश है। इस आवेश विन्यास के कारण घन के केन्द्र पर विद्युत विभव तथा विद्युत-क्षेत्र ज्ञात कीजिए।
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q13
हल-
चित्र 2.6 में घन की भुजा = b
अतः घन का प्रत्येक विकर्ण = $\sqrt { { b }^{ 2 }+{ b }^{ 2 }+{ b }^{ 2 } }$ = b√3
घन के प्रत्येक शीर्ष पर स्थित आवेश = q तथा प्रत्येक आवेश की घन के केन्द्र O (चारों विकर्णो AF, EB, CH तथा GD का छेदन बिन्दु, जो इनका मध्य बिन्दु होता है) से दूरी

चूंकि प्रत्येक विकर्ण के शीर्ष पर समान परिमाण तथा समान प्रकृति के आवेश रिथत हैं, अतः इनके कारण.O पर तीव्रता परिमाण में बराबर तथा दिशा में विपरीत होगी। अतः ये एक-दूसरे को निरस्त कर देंगी। अतः O पर परिणामी तीव्रता शून्य होगी।

प्रश्न 14.
1.5 μC और 2.5 μC आवेश वाले दो सूक्ष्म गोले 30 cm दूर स्थित हैं।
(a) दोनों आवेशों को मिलाने वाली रेखा के मध्य बिन्दु पर, और
(b) मध्य बिन्दु से होकर जाने वाली रेखा के अभिलम्ब तल में मध्य बिन्दु से 10 cm दूर स्थित किसी बिन्दु पर विभव और विद्युत-क्षेत्र ज्ञात कीजिए।
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q14
हल-
(a) मध्य बिन्दु की प्रत्येक आवेश से दूरी
r_A = r_B = 0.15 m
मध्य बिन्दु पर विभव

प्रश्न 15.
आन्तरिक त्रिज्या तथा बाह्य त्रिज्या r₁ वाले एक गोलीय चालक खोल (कोश) पर r₂ आवेश है।
(a) खोल के केन्द्र पर एक आवेश q रखा जाता है। खोल के भीतरी और बाहरी पृष्ठों पर पृष्ठ आवेश घनत्व क्या है?
(b) क्या किसी कोटर (जो आवेश विहीन है) में विद्युत-क्षेत्र शून्य होता है, चाहे खोल गोलीय न होकर किसी भी अनियमित आकार का हो? स्पष्ट कीजिए।
हल-
(a) जब चालक को केवल Q आवेश दिया गया है तो यह पूर्णत: चालक के बाह्य पृष्ठ पर रहता है। हम जानते हैं कि एक चालक के भीतर नैट आवेश शून्य रहता है; अतः खोल के केन्द्र पर q आवेश रखने पर, खोल की भीतरी सतह पर -q आवेश प्रेरित हो जाता है तथा बाहरी सतह पर अतिरिक्त + q आवेश आ जाता है।

(b) हाँ, यदि कोटर आवेशविहीन है तो उसके अन्दर विद्युत-क्षेत्र शून्य होगा। इसके विपरीत कल्पना करें कि किसी चालक के भीतर एक अनियमित आकृति का आवेशविहीन कोटर है जिसके भीतर विद्युत-क्षेत्र शून्य नहीं है। अब एक ऐसे बन्द लूप पर विचार करें जिसका कुछ भाग कोटर के भीतर क्षेत्र रेखाओं के समान्तर है तथा शेष भाग कोटर से बाहर परन्तु चालक के भीतर है। चूंकि चालक के भीतर विद्युत-क्षेत्र शून्य है; अतः यदि एकांक आवेश को इस बन्द लूप के अनुदिश ले जाया जाए तो क्षेत्र द्वारा किया गया नैट कार्य प्राप्त होगा। परन्तु यह स्थिति स्थिरविद्युत क्षेत्र के लिए सत्य नहीं है (बन्द लूप पर नैट कार्य शून्य होता है)। अत: हमारी परिकल्पना कि कोटर के भीतर विद्युत-क्षेत्र शून्य नहीं है, गलत है। अर्थात् चालक के भीतर आवेशविहीन कोटर के भीतर विद्युत-क्षेत्र शून्य होगा।

प्रश्न 16.
(a) दर्शाइए कि आवेशित पृष्ठ के एक पाश्र्व से दूसरे पाश्र्व पर स्थिरविद्युत-क्षेत्र के अभिलम्ब घटक में असांतत्य होता है, जिसे
$\left( \vec { {E}_{2} } -\vec { {E}_{1} } \right) \hat { n } =\frac { \sigma }{ { \varepsilon }_{ 0 } }$
द्वारा व्यक्त किया जाता है। जहाँ एक बिन्दु पर पृष्ठ के अभिलम्ब एकांक सदिश है तथा $\sigma$ उस बिन्दु पर पृष्ठ आवेश घनत्व है ( $\overset { \wedge }{ n }$ की दिशा पाश्र्व 1 से पाश्र्व 2 की ओर है)। अतः
दर्शाइए कि चालक के ठीक बाहर विद्युत-क्षेत्र $\frac { \sigma \hat { n } }{ { \varepsilon }_{ 0 } }$ है।
(b) दर्शाइए कि आवेशित पृष्ठ के एक पाश्र्व से दूसरे पाश्र्व पर स्थिरविद्युत-क्षेत्र का स्पर्शीय घटक संतत है।
[संकेत- (a) के लिए गौस-नियम का उपयोग कीजिए। (b) के लिए इस तथ्य का उपयोग करें कि संवृत पाश पर एक स्थिर वैद्युत क्षेत्र द्वारा किया गया कार्य शून्य होता है।)
उत्तर-
(a) माना AB एक आवेशित पृष्ठ है जिस पर पृष्ठीय आवेश घनत्व $\sigma$ है। पृष्ठ के समीप प्रत्येक बिन्दु पर विद्युत-क्षेत्र $\overrightarrow { E }$ समान तथा पृष्ठ के लम्बवत् बाहर की ओर है।
चित्र में एक बेलनाकार गाउसीय पृष्ठ को प्रदर्शित किया गया है। इस पृष्ठ के वृत्ताकार परिच्छेदों पर अभिलम्ब सदिश ${ \overset { \wedge }{ n } }_{ 1 }$ व ${ \overset { \wedge }{ n } }_{ 2 }$ क्रमश: क्षेत्रों $\overrightarrow { { E }_{ 1 } }$ व $\overrightarrow { { E }_{ 2 } }$ के समदिश हैं जबकि वक्र पृष्ठ पर अभिलम्ब संगत क्षेत्र $\overrightarrow { { E }_{ 3 } }$ के लम्बवत् हैं।
माना प्रत्येक वृत्तीय परिच्छेद का क्षेत्रफल ΔA है तब गाउसीय पृष्ठ से गुजरने वाला विद्युत फ्लक्स
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q16

(b) आवेशित पृष्ठ के एक ओर से दूसरी ओर जाने पर स्थिरविद्युत-क्षेत्र का स्पर्श रेखीय घटक सतत (सर्वथा शून्य) होता है, अन्यथा पृष्ठ के विभिन्न बिन्दु अलग-अलग विभवों पर होंगे तथा धनावेश पृष्ठ के अनुदिश उच्च विभव से निम्न विभव के बिन्दुओं की ओर गति करता रहेगा।

प्रश्न 17.
रैखिक आवेश घनत्व λ वाला एक लम्बा आवेशित बेलन एक खोखले समाक्षीय चालक बेलन द्वारा घिरा है। दोनों बेलनों के बीच के स्थान में विद्युत-क्षेत्र कितना है?

प्रश्न 18.
एक हाइड्रोजन परमाणु में इलेक्ट्रॉन तथा प्रोटॉन लगभग 0.53 Å दूरी पर परिबद्ध हैं:
(a) निकाय की स्थितिज ऊर्जा का eV में परिकलन कीजिए, जबकि प्रोटॉन व इलेक्ट्रॉन के मध्य की अनन्त दूरी पर स्थितिज ऊर्जा को शून्य माना गया है।
(b) इलेक्ट्रॉन को स्वतन्त्र करने में कितना न्यूनतम कार्य करना पड़ेगा, यदि यह दिया गया है कि इसकी कक्षा में गतिज ऊर्जा (a) में प्राप्त स्थितिज ऊर्जा के परिमाण की आधी है?
(c) यदि स्थितिज ऊर्जा को 1.06 Å पृथक्करण पर शून्य ले लिया जाए तो, उपर्युक्त (a) और (b) के उत्तर क्या होंगे?
हल-
यहाँ q₁ = -1.6 x 10^-19 C, q₂ = +1.6 x 10^-19 C
r = 0.53 Å = 5.3 x 10^-11 m

प्रश्न 19.
यदि H, अणु के दो में से एक इलेक्ट्रॉन को हटा दिया जाए तो हमें हाइड्रोजन आण्विक आयन(H₂⁺) प्राप्त होगा। (H₂⁺) की निम्नतम अवस्था (ground state) में दो प्रोटॉन के बीच दूरी लगभग 1.5 Å है और इलेक्ट्रॉन प्रत्येक प्रोटॉन से लगभग 1 Å की दूरी पर है। निकाय की स्थितिज ऊर्जा ज्ञात कीजिए। स्थितिज ऊर्जा की शून्य स्थिति के चयन का उल्लेख कीजिए।
हल-
स्थितिज ऊर्जा की शुन्य स्थितिअनन्त पर मानते हुए दिए गए वैद्युत निकाय (जिसमें चित्र 2.12 के । अनुसार दो प्रोटॉम एवं एक इलेक्ट्रॉन है) की स्थितिज ऊर्जा
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q19

प्रश्न 20.
a और b त्रिज्याओं वाले दो आवेशित चालक गोले एक तार द्वारा एक-दूसरे से जोड़े गए हैं। दोनों गोलों के पृष्ठों पर विद्युत-क्षेत्रों में क्या अनुपात है? प्राप्त परिणाम को, यह समझाने में प्रयुक्त कीजिए कि किसी एक चालक के तीक्ष्ण और नुकीले सिरों पर आवेश घनत्व, चपटे भागों की अपेक्षा अधिक क्यों होता है?

UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q20.1

प्रश्न 21.
बिन्दु (0, 0, -a) तथा (0, 0, a) पर दो आवेश क्रमशः -q और +q स्थित हैं।
(a) बिन्दुओं (0, 0, z) और (x, y, 0) पर स्थिरविद्युत विभव क्या है?
(b) मूल बिन्दु से किसी बिन्दु की दूरी पर विभव की निर्भरता ज्ञात कीजिए, जबकि $\frac { r }{ a }$ >> 1
(c) x-अक्ष पर बिन्दु (5, 0, 0) से बिन्दु (-7, 0, 0) तक एक परीक्षण आवेश को ले जाने में कितना कार्य करना होगा? यदि परीक्षण आवेश को उन्हीं बिन्दुओं के बीच x-अक्ष से होकर न ले जाएँ तो क्या उत्तर बदल जाएगा?
हल-
दिए गए बिन्दु आवेश एक विद्युत द्विध्रुव बनाते हैं।
आवेशों के बीच की दूरी = 2a

UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q21.1

प्रश्न 22.
नीचे दिए गए चित्र 2.14 में एक आवेशविन्यास जिसे विद्युत चतुर्भुवी कहा जाता है, दर्शाया गया है। चतुर्भुवी के अक्ष पर स्थित किसी बिन्दु के लिए पर विभव की निर्भरता प्राप्त कीजिए जहाँ $\frac { r }{ a }$ >> 1। अपने परिणाम की तुलना एक विद्युत द्विध्रुव व विद्युत एकल ध्रुव (अर्थात् किसी एकल आवेश) के लिए प्राप्त परिणामों से कीजिए।
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q22
हल-
माना P की विभिन्न आवेशों से दूरियाँ निम्नलिखित हैं-
r – a, r, r + a
चतुर्भुवी होने के कारण बिन्दु P पर विद्युत विभव

प्रश्न 23.
एक विद्युत टैक्नीशियन को 1 kV विभवान्तर के परिपथ में 2 μF संधारित्र की आवश्यकता है। 1 μF के संधारित्र उसे प्रचुर संख्या में उपलब्ध हैं जो 400 V से अधिक का विभवान्तर वहन नहीं कर सकते। कोई सम्भव विन्यास सुझाइए जिसमें न्यूनतम संधारित्रों की आवश्यकता हो।
हल-
माना हम प्रत्येक पंक्ति में n संधारित्र जोड़ते हैं तथा ऐसी m पंक्तियों को समान्तर क्रम में जोड़ते हैं।
श्रेणीक्रम में, 1 kV = 1000 V को विभवान्तर n संधारित्रों में बराबर बँट जाएगा।
प्रत्येक संधारित्र पर विभवान्तर = $\frac { 1000 }{ n }$

हमें 3-3 संधारित्रों को श्रेणीक्रम में जोड़कर इस प्रकार की 6 पंक्तियाँ बनानी होंगी। अब इन 6 पंक्तियों को समान्तर क्रम में जोड़ना होगा।

प्रश्न 24.
2F वाले एक समान्तर पट्टिका संधारित्र की पट्टिका का क्षेत्रफल क्या है, जबकि पट्टिकाओं का पृथकन 0.5 cm है? [अपने उत्तर से आप यह समझ जाएँगे कि सामान्य संधारित्र uF या कम परिसर के क्यों होते हैं? तथापि विद्युत-अपघटन संधारित्रों (Electrolytic capacitors) की धारिता कहीं अधिक (0.1 F) होती है क्योंकि चालकों के बीच अति सूक्ष्म पृथकन होता है।
हल-
दिया है, समान्तर पट्ट संधारित्र की धारिता C = 2F.
इसकी प्लेटों के बीच पृथक्करण (दूरी) d= 0.5 cm = 5 x 10^-3 m
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q24

प्रश्न 25.
चित्र 2.15 के नेटवर्क (जाल) की तुल्य धारिता प्राप्त 100 pF कीजिए। 300 V संभरण (सप्लाई) के साथ प्रत्येक संधारित्र का आवेश व उसकी वोल्टता ज्ञात कीजिए।
हल-
दिए गए नेटवर्क को संलग्न चित्र 2.16 की भाँति व्यवस्थित किया जा सकता है-
सर्वप्रथम C₂ व C₃ श्रेणीक्रम में जुड़े हैं, इनकी तुल्य धारिता

शेष संयोजन का विभवान्तर V = 300 V – 200 V = 100 V
C₁, C₂ व C₃ के श्रेणी संयोजन से समान्तर क्रम में जुड़ा है,
C₁ का विभवान्तर = 100 V
तथा C₂ व C₃ के श्रेणी संयोजन का विभवान्तर = 100 V
C₁ पर आवेश q₁ = C₁V₁ = 100 x 10^-12 F x 100 V = 10^-8 C
C₂ = C₃; अतः कुल विभवान्तर 100 V इन पर बराबर-बराबर बंटेगा।
प्रत्येक का विभवान्तर = 50 V
प्रत्येक पर आवेश q₂ = C₂V₂ = 200 x 10^-12 F x 50 V = 10^-8 C
अतः संयोजन की धारिता C = $\frac { 200 }{ 3 }$ pF
C₁ का विभवान्तर = 100 V तथा आवेश = 10^-8 C
C₂ का विभवान्तर = 50 V तथा आवेश = 10^-8 C
C₃ का विभवान्तर = 50 V तथा आवेश = 10^-8 C
C₄ का विभवान्तर = 200 V तथा आवेश = 2 x 10^-8 C

प्रश्न 26.
किसी समान्तर पट्टिका संधारित्र की प्रत्येक पट्टिका का क्षेत्रफल 90 cm² है और उनके बीच पृथकन 2.5 mm है। 400 V संभरण से संधारित्र को आवेशित किया गया है।
(a) संधारित्र कितना स्थिरविद्युत ऊर्जा संचित करता है?
(b) इस ऊर्जा को पट्टिकाओं के बीच स्थिरविद्युत-क्षेत्र में संचित समझकर प्रति एकांक आयतन ऊर्जा u ज्ञात कीजिए। इस प्रकार, पट्टिकाओं के बीच विद्युत-क्षेत्र E के परिमाण और u में सम्बन्ध स्थापित कीजिए।

प्रश्न 27.
एक 4 μF के संधारित्र को 200 V संभरण (सप्लाई) से आवेशित किया गया है। फिर संभरण से हटाकर इसे एक अन्य अनावेशित 2 μF के संधारित्र से जोड़ा जाता है। पहले संधारित्र की कितनी स्थिरविद्युत ऊर्जा का ऊष्मा और विद्युत चुम्बकीय विकिरण के रूप में ह्रास होता है?
हल-
दिया है, C₁ = 4 x 10^-6 F, V₁ = 200 V, C₂ = 2 x 10^-6 F, V₂ = 0 V
माना जोड़ने के पश्चात् दोनों का उभयनिष्ठ विभव V है।
जोड़ने से पूर्व संभरण को हटा लिया गया है; अतः कुल आवेश स्थिर रहेगा।

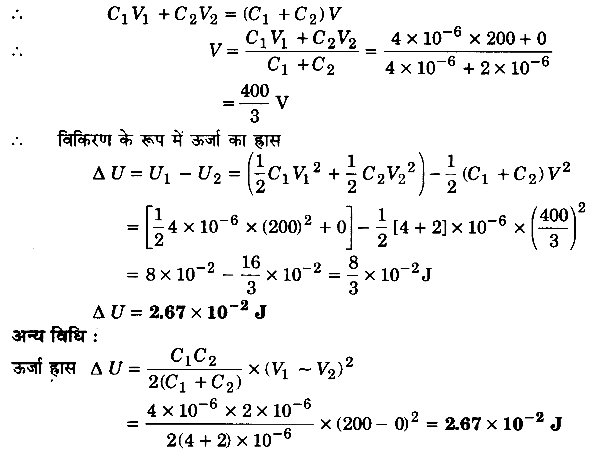
प्रश्न 28.
दर्शाइए कि एक समान्तर पट्टिका संधारित्र की प्रत्येक पट्टिका पर बल का परिमाण $\frac { 1 }{ 2 }$ QE है, जहाँ संधारित्र पर आवेश है और E पट्टिकाओं के बीच विद्युत-क्षेत्र का परिमाण है। घटक $\frac { 1 }{ 2 }$ के मूल को समझाइए।
हल-
माना दोनों पट्टिकाओं के बीच लगने वाला पारस्परिक आकर्षण बल F है तथा प्लेटों के बीच की दूरी है। दूरी x में dx की वृद्धि करने पर आकर्षण बल F के विरुद्ध कृत कार्य
dW = F dx …..(i)
प्लेटों के बीच विद्युत-क्षेत्र E है; अत: संधारित्र के एकांक आयतन में संचित ऊर्जा $u=\frac { 1 }{ 2 } { \varepsilon }_{ 0 }{ E }^{ 2 }$
प्लेटों का क्षेत्रफल A व बीच की दूरी ४ है; अत: संधारित्र की कुल ऊर्जा
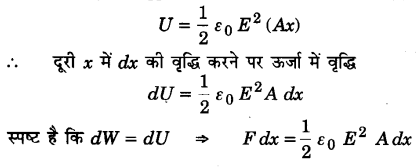
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q28

घटक $\frac { 1 }{ 2 }$ का मूल इस तथ्य में निहित है कि चालक प्लेट के बाहर विद्युत-क्षेत्र $\frac { E }{ 2 }$ तथा प्लेट के भीतर शून्य होता है। अत: औसत विद्युत-क्षेत्र में होता है, जिसके विरुद्ध प्लेट को खिसकाया जाता है।

प्रश्न 29.
दो संकेन्द्री गोलीय चालकों जिनको उपयुक्त विद्युतरोधी आलम्बों से उनकी स्थिति में रोका गया है, से मिलकर एक गोलीय संधारित्र बना है (चित्र 2.17)। दर्शाइए कि गोलीय संधारित्र की धारिता C इस प्रकार व्यक्त की जाती है:

उत्तर-
गोलीय अथवा गोलाकार संधारित्र की धारिता (Capacitance of Spherical Capacitor) का व्यंजक-माना गोलीय संधारित्र धातु के दो समकेन्द्रीय खोखले गोलों A व B का बना है, जो एक-दूसरे को कहीं भी स्पर्श नहीं करते (चित्र 2.17)। जब गोले A को-q आवेश दिया जाता है तो प्रेरण द्वारा गोले B पर +q आवेश उत्पन्न हो जाता है। चूंकि गोले B का बाहरी तल पृथ्वी से जुड़ा है; अतः गोले B के बाहरी तल पर उत्पन्न -q आवेश पृथ्वी से आने वाले इलेक्ट्रॉनों से निरावेशित हो जाता है। इस प्रकार गोले B के आन्तरिक पृष्ठ पर +q आवेश रह जाता है। माना गोले A की त्रिज्या r2 तथा गोले B की त्रिज्या b है।
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q29.1

प्रश्न 30.
एक गोलीय संधारित्र के भीतरी गोले की त्रिज्या 12 cm है तथा बाहरी गोले की त्रिज्या 13 cm है। बाहरी गोला भू-सम्पर्कित है तथा भीतरी गोले पर 2.5 μC का आवेश दिया गया है। संकेन्द्री गोलों के बीच के स्थान में 32 परावैद्युतांक का द्रव भरा है।
(a) संधारित्र की धारिता ज्ञात कीजिए।
(b) भीतरी गोले का विभव क्या है?
(c) इस संधारित्र की धारिता की तुलना एक 12 cm त्रिज्या वाले किसी वियुक्त गोले की धारिता से कीजिए। व्याख्या कीजिए कि गोले की धारिता इतनी कम क्यों है?
हल-
दिया है, r₁ = 13 cm = 0.13 m, r₂ = 0.12 m, K = 32, Q = 2.5 x 10^-6 C
(a) गोलीय संधारित्र की धारिता

अर्थात् गोलीय संधारित्र की धारिता एकल गोले की धारिता से 416 गुनी अधिक है। इससे यह निष्कर्ष प्राप्त होता है कि एकल चालक के समीप एक अन्य भू-सम्पर्कित चालक रखकर उनके बीच के स्थान में परावैद्युत भरने से धारिता बहुत अधिक बढ़ जाती है।

प्रश्न 31.
सावधानीपूर्वक उत्तर दीजिए :

दो बड़े चालक गोले जिन पर आवेश Q₁ और Q₂ हैं, एक-दूसरे के समीप लाए जाते हैं। क्या इनके बीच स्थिर विद्युत बल का परिमाण तथ्यत:
$\frac { { Q }_{ 1 }{ Q }_{ 2 } }{ 4\Pi { \varepsilon }_{ 0 }{ r }^{ 2 } }$
द्वारा दर्शाया जाता है, जहाँ r इनके केन्द्रों के बीच की दूरी है।
यदि कूलॉम के नियम में $\frac { { 1 } }{ { r }^{ 3 } }$ निर्भरता का समावेश ( $\frac { { 1 } }{ { r }^{ 2 } }$ के स्थान पर) हो तो क्या गाउस का नियम अभी भी सत्य होगा?
स्थिरविद्युत-क्षेत्र विन्यास में एक छोटा परीक्षण आवेश किसी बिन्दु पर विराम में छोड़ा जाता है। क्या यह उस बिन्दु से होकर जाने वाली क्षेत्र रेखा के अनुदिश चलेगा?
इलेक्ट्रॉन द्वारा एक वृत्तीय कक्षा पूरी करने में नाभिक के क्षेत्र द्वारा कितना कार्य किया जाता है? यदि कक्षा दीर्घवृत्ताकार हो तो क्या होगा?
हमें ज्ञात है कि एक आवेशित चालक के पृष्ठ के आर-पार विद्युत-क्षेत्र असंतत होता है। क्या वहाँ विद्युत विभव भी असंतत होगा?
किसी एकल चालक की धारिता से आपका क्या अभिप्राय है?
एक सम्भावित उत्तर की कल्पना कीजिए कि पानी का परावैद्युतांक (= 80), अभ्रक के परावैद्युतांक (= 6) से अधिक क्यों होता है?

हल-

यदि दोनों गोले एक-दूसरे से बहुत अधिक दूरी पर होंगे तभी वे बिन्दं आवेशों की भाँति कार्य करेंगे। कूलॉम का नियम केवल बिन्दु आवेशों के लिए सत्य है; अत: गोलों को समीप लाने पर कूलॉम का नियम लागू नहीं होगा।
नहीं, गाउस का नियम केवल तभी तक सत्य है जब तक कि कूलॉम के नियम में निर्भरता $\frac { { 1 } }{ { r }^{ 2 } }$ अतः कूलॉम के नियम में निर्भरता ( $\frac { { 1 } }{ { r }^{ 3 } }$ ) होने पर गाउस का नियम लागू नहीं होगा।
नहीं, यदि क्षेत्र रेखा एक सरल रेखा है, केवल तभी परीक्षण आवेश क्षेत्र रेखा के अनुदिश चलेगा।
शून्य, स्थिर विद्युत क्षेत्र में बिन्दु आवेश के बन्द वक्र पर चलाने में किया गया कार्य शून्य होता है। यदि वक्र दीर्घवृत्ताकार है तो भी कार्य शून्य होगा।
नहीं, चालक की पूरी सतह पर विद्युत विभव सतत होता है।
एकल चालक की धारिता एक ऐसे संधारित्र की धारिता है, जिसकी दूसरी प्लेट अनन्त पर है।
जल के अणुओं का अपना स्थायी द्विध्रुव आघूर्ण होता है; अत: जल का परावैद्युतांक उच्च होता है, इसके विपरीत अभ्रक के अणुओं का द्विध्रुव आघूर्ण शून्य होता है; अत: इसका परावैद्युतांक निम्न होता है।

प्रश्न 32.
एक बेलनाकार संधारित्र में 15 cm लम्बाई एवं त्रिज्याएँ 1.5 cm तथा 1.4 cm के दो समाक्ष बेलन हैं। बाहरी बेलन भू-सम्पर्कित है और भीतरी बेलन को 3.5 μF का आवेश दिया गया है। निकाय की धारिता और भीतरी बेलन का विभव ज्ञात कीजिए। अन्त्य प्रभाव (अर्थात सिरों पर क्षेत्र रेखाओं का मुड़ना) की उपेक्षा कर सकते हैं।

प्रश्न 33.
3 परावैद्युतांक तथा 10⁷ Vm^-1 की परावैद्युत सामर्थ्य वाले एक पदार्थ से 1 kV वोल्टता अनुमतांक के समान्तर पट्टिका संधारित्र की अभिकल्पना करनी है। [परावैद्यत सामर्थ्य वह अधिकतम विद्युत-क्षेत्र है जिसे कोई पदार्थ बिना भंग हुए अर्थात आंशिक आयनन द्वारा बिना विद्युत संचरण आरम्भ किए सहन कर सकता है। सुरक्षा की दृष्टि से क्षेत्र को कभी भी परावैद्युत सामर्थ्य के 10% से अधिक नहीं होना चाहिए।] 50 pF धारिता के लिए पट्टिकाओं का कितना न्यूनतम क्षेत्रफल होना चाहिए?

प्रश्न 34.
व्यवस्थात्मकतः निम्नलिखित में संगत समविभव पृष्ठ का वर्णन कीजिए :

z-दिशा में अचर विद्युत-क्षेत्र
एक क्षेत्र जो एकसमान रूप से बढ़ता है, परन्तु एक ही दिशा (मान लीजिए z-दिशा) में रहता है।
मूल बिन्दु पर कोई एकल धनावेश, और
एक समतल में समान दूरी पर समान्तर लम्बे आवेशित तारों से बने एकसमान जाल।

उत्तर-

x-y समतल के समान्तर समतल।
समविभव पृष्ठ x-y समतल के समान्तर होंगे, परन्तु बढ़ते क्षेत्र के साथ, भिन्न-भिन्न नियत विभव वाले समतल एक-दूसरे के समीप होते जाएँगे।
संकेन्द्रीय गोले जिनके केन्द्र मूल बिन्दु पर हैं।
ग्रिड के समीप, समविभव पृष्ठों की आकृति समय के साथ बदलेगी परन्तु ग्रिड से दूर जाने पर समविभव पृष्ठ ग्रिड (जाल) के अधिकाधिक समान्तर होते जाएँगे।

प्रश्न 35.
किसी वान डे ग्राफ प्रकार के जनित्र में एक गोलीय धातु कोश 15 x 10⁶ V का एक इलेक्ट्रोड बनाना है। इलेक्ट्रोड के परिवेश की गैस की परावैद्युत सामर्थ्य 5 x 10⁷ Vm^-1 है। गोलीय कोश की आवश्यक न्यूनतम त्रिज्या क्या है? [इस अभ्यास से आपको यह ज्ञान होगा कि एक छोटे गोलीय कोश से आप स्थिरवैद्यत जनित्र, जिसमें उच्च विभव प्राप्त करने के लिए कम आवेश की आवश्यकता होती है, नहीं बना सकते।
हल-
दिया है, गोलीय कोश का विभव V = 15 x 10⁶ V
गैस की परावैद्युत सामर्थ्य E_max = 5 x 10⁷ V/m
माना कोश की न्यूनतम त्रिज्या r है, तब
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance Q35

प्रश्न 36.
r₁ त्रिज्या तथा q₁ आवेश वाला एक छोटा गोला r₂ त्रिज्या और q₂ आवेश के गोली खोल (कोश) से घिरा है। दर्शाइए यदि q₁ धनात्मक है तो (जब दोनों को एक तार द्वारा जोड़ दिया जाता है) आवश्यक रूप से आवेश, गोले से खोल की तरफ ही प्रवाहित होगा, चाहे खोल पर आवेश q₂ कुछ भी हो।
उत्तर-
हम जानते हैं कि किसी चालक का सम्पूर्ण आवेश उसके बाह्य पृष्ठ पर रहता है; अतः जैसे ही दोनों गोलों को चालक तार द्वारा जोड़ा जाएगा वैसे ही अन्दर वाले छोटे गोले को सम्पूर्ण आवेश तार से होकर बाहरी खोल की ओर प्रवाहित हो जाएगा, चाहे खोल पर आवेश q₂ कुछ भी क्यों न हो।

प्रश्न 37.
निम्न का उत्तर दीजिए:
(a) पृथ्वी के पृष्ठ के सापेक्ष वायुमण्डले की ऊपर परत लगभग 400 kV पर है, जिसके संगत विद्युत-क्षेत्र ऊँचाई बढ़ने के साथ कम होता है। पृथ्वी के पृष्ठ के सापेक्ष विद्युत-क्षेत्र लगभग 100 Vm^-1 है। तब फिर जब हम घर से बाहर खुले में जाते हैं तो हमें विद्युत आघात क्यों नहीं लगता? (घर को लोहे का पिंजरा मान लीजिए; अतः उसके अन्दर कोई विद्युत-क्षेत्र नहीं है।)

(b) एक व्यक्ति शाम के समय अपने घर के बाहर 2 m ऊँचा अवरोधी पट्ट रखता है जिसके शिखर पर एक 1 m क्षेत्रफल की बड़ी ऐलुमिनियम की चादर है। अगली सुबह वह यदि धातु की चादर को छूता है तो क्या उसे विद्युत आघात लगेगा?

(c) वायु की थोड़ी-सी चालकता के कारण सारे संसार में औसतन वायुमण्डल में विसर्जन धारा 1800 A मानी जाती है। तब यथासमय वातावरण स्वयं पूर्णतः निरावेशित होकर विद्युत उदासीन क्यों नहीं हो जाता? दूसरे शब्दों में, वातावरण को कौन आवेशित रखता है?

(d) तड़ित के दौरान वातावरण की विद्युत ऊर्जा, ऊर्जा के किन रूपों में क्षयित होती है?
[संकेत : पृष्ठ आवेश घनत्व = 10^-9 Cm^-2 के अनुरूप पृथ्वी के (पृष्ठ) पर नीचे की दिशा में लगभग 100 Vm^-1 का विद्युत क्षेत्र होता है। लगभग 50 km ऊँचाई तक (जिसके बाहर यह अच्छा चालक है) वातावरण की थोड़ी सी चालकता के कारण लगभग + 1800 C का आवेश प्रति सेकण्ड समग्र रूप से पृथ्वी में पंप होता रहता है। तथापि, पृथ्वी निरावेशित नहीं होती, क्योंकि संसार में हर समय लगातार तड़ित तथा तड़ित-झंझा होती रहती है, जो समान मात्रा में ऋणावेश पृथ्वी में पंप कर देती है।]
उत्तर-
(a) हमारा शरीर तथा पृथ्वी के समान विभव पर रहने के कारण हमारे शरीर से होकर कोई विद्युत धारा प्रवाहित नहीं होती इसीलिए हमें कोई विद्युत आघात नहीं लगता।

(b) हाँ, पृथ्वी तथा ऐलुमिनियम की चादर मिलकर एक संधारित्र बनाती हैं तथा अवरोधी पट्ट परावैद्युत का कार्य करती है। ऐलुमिनियम की चादर वायुमण्डलीय आवेश के लगातार गिरते रहने से आवेशित होती रहती है और उच्च विभव प्राप्त कर लेती है; अतः जब व्यक्ति इस चादर को छूता है तो उसके शरीर से होकर एक विद्युत धारा प्रवाहित होती है और इस कारण उस व्यक्ति को विद्युत आघात लगेगा।

(c) यद्यपि वायुमण्डल 1800 A की औसत विसर्जन धारा के कारण लगातार निरावेशित होता रहता है। परन्तु साथ ही तड़ित तथा झंझावात के कारण यह लगातार आवेशित भी होता रहता है और इन दोनों के बीच एक सन्तुलन बना रहता है जिससे कि वायुमण्डल कभी भी पूर्णत: निरावेशित नहीं हो पाता।

(d) तड़ित के दौरान वातावरण की विद्युत ऊर्जा, प्रकाश ऊर्जा, ध्वनि ऊर्जा तथा ऊष्मीय ऊर्जा के रूप में क्षयित होती है।

परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न

प्रश्न 1.
वैद्युत विभव का मात्रक है (2011, 14)
(i) जूल/कूलॉम
(ii) जूल x कूलॉम
(iii) कूलॉम/जूल
(iv) न्यूटन/कूलॉम
उत्तर-
(i) जूल/कूलॉम

प्रश्न 2.
E = 0 तीव्रता वाले वैद्युत-क्षेत्र में विभव V का दूरी r के साथ परिवर्तन होग (2010, 12, 17)
(i) V ∝ $\frac { 1 }{ r }$
(ii) V ∝ r
(iii) V ∝ $\frac { { 1 } }{ { r }^{ 2 } }$
(iv) V, r पर निर्भर नहीं करेगा
उत्तर-
(iv) V, r पर निर्भर नहीं करेगा

प्रश्न 3.
दो प्लेटें एक-दूसरे से 1 सेमी दूरी पर हैं और उनमें विभवान्तर 10 वोल्ट है। प्लेटों के बीच वैद्युत-क्षेत्र की तीव्रता है- (2009)
(i) 10 न्यूटन/कूलॉम
(ii) 500 न्यूटन/कूलॉम
(iii) 1000 न्यूटन/कूलॉम
(iv) 250 न्यूटन/कूलॉम
उत्तर-
(iii) 1000 न्यूटन/कूलॉम

प्रश्न 4.
1 इलेक्ट्रॉन वोल्ट (eV) मात्रक है
(i) ऊर्जा का
(ii) विभव का
(iii) वेग का
(iv) कोणीय संवेग का
उत्तर-
(i) ऊर्जा का

प्रश्न 5.
एक वोल्ट विभवान्तर पर त्वरित करने पर इलेक्ट्रॉन की ऊर्जा होती है|
(i) 1 जूल
(ii) 1 इलेक्ट्रॉन-वोल्ट
(iii) 1 अर्ग
(iv) 1 वाट
उत्तर-
(ii) 1 इलेक्ट्रॉन-वोल्ट

प्रश्न 6.
वैद्युत द्विध्रुव के कारण, केन्द्र से दूरी पर अक्ष में स्थित बिन्दु पर विद्युत क्षेत्र की तीव्रता एवं विभव क्रमशः E तथा V हैं। E तथा V में सम्बन्ध होगा (2017)
(i) E = $\frac { V }{ R }$
(ii) E = $\frac { V }{ 2r }$
(iii) E = $\frac { 2V }{ r }$
(iv) E = 2rV
उत्तर-
(i) E = $\frac { V }{ R }$

प्रश्न 7.
निम्न में से कौन-सा तथ्य समविभव पृष्ठ के लिए सत्य नहीं है ? (2009)
(i) पृष्ठ पर किन्हीं दो बिन्दुओं के बीच विभवान्तर शून्य होता है।
(ii) वैद्युत बल रेखाएँ पृष्ठ के सर्वथा लम्बवत् होती हैं।
(iii) पृष्ठ पर किसी आवेश को एक स्थान से दूसरे स्थान पर ले जाने पर कोई कार्य नहीं होता है।
(iv) समविभव पृष्ठ सर्वदा गोलाकार होते हैं।
उत्तर-
(iv) समविभव पृष्ट सर्वदा गोलाकार होते हैं।

प्रश्न 8.
एक इलेक्ट्रॉन को दूसरे इलेक्ट्रॉन के अधिक नजदीक लाने पर निकाय की वैद्युत स्थितिज ऊर्जा (2010)
(i) घटती है।
(ii) बढ़ती है।
(iii) उतनी ही रहती है।
(iv) शून्य हो जाती है।
उत्तर-
(ii) बढ़ती है।

प्रश्न 9.
वायु में 1 सेमी दूरी पर रखे प्रत्येक 1 माइक्रो कूलॉम के दो धनात्मक बिन्दु आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा है- (2016)
(i) 0.9 इलेक्ट्रॉन-वोल्ट
(ii) 0.9 जूल
(iii) 1 जूल
(iv) 9 जूल
उत्तर-
(ii) 0.9 जूल

प्रश्न 10.
निम्नलिखित में से धारिता का मात्रक कौन-सा है?
(i) कूलॉम
(ii) ऐम्पियर
(iii) वोल्ट
(iv) कूलॉम/वोल्ट
उत्तर-
(iv) कूलॉम/वोल्ट

प्रश्न 11.
एक आवेशित संधारित्र बैटरी से जुड़ा है। यदि प्लेटों के बीच परावैद्युत पदार्थ की एक पट्टी रखी जाये तो निम्न में से क्या परिवर्तित नहीं होगा ? (2010)
(i) आवेश
(ii) विभवान्तर
(iii) धारिता
(iv) ऊर्जा
उत्तर-
(ii) विभवान्तर

प्रश्न 12.
वायु में रखे दो धनावेशों के मध्य परावैद्युत पदार्थ रख देने पर इनके बीच प्रतिकर्षण बल का मान (2015)
(i) बढ़ जायेगा
(ii) घट जायेगा
(iii) वही रहेगा।
(iv) शून्य
उत्तर-
(ii) घट जायेगा।

प्रश्न 13.
दिये गये चित्र 2.18 में बिन्दुओं A व B के बीच तुल्य धारिता है

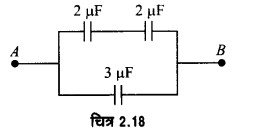
(i) 4 μF
(ii) $\frac { 12 }{ 7 }$ μF
(iii) $\frac { 1 }{ 4 }$ μF
(iv) $\frac { 7 }{ 12 }$ μF
उत्तर-
(i) 4 μF

प्रश्न 14.
दिये गये चित्र 2.19 में बिन्दुओं A व B के बीच तुल्य धारिता है- (2009)

(i) $\frac { 2 }{ 3 }$ μF
(i) $\frac { 3 }{ 2 }$ μF
(ii) $\frac { 11 }{ 3 }$ μF
(iv) 1 μF
उत्तर-
(i) 1 μF

प्रश्न 15.
चित्र 2.20 में प्रदर्शित संधारित्रों की तुल्य धारिता A व B के बीच है (2015)

(i) 4 μF
(ii) 2.5 μF
(iii) 2 μF
(iv) 0.25 μF
उत्तर-
(ii) 2.5 μF

प्रश्न 16.
100 माइक्रोफैरड धारिता वाले संधारित्र को 10 वोल्ट तक आवेशित करने पर उसमें संचित ऊर्जा होगी (2016)
(i) 5.0 x 10^-3 जूल
(ii) 0.5 x 10^-3 जूल।
(iii) 0.5 जूल।
(iv) 5.0 जूल।
उत्तर-
(i) 5.0 x 10^-3 जूल।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
वैद्युत-विभव की परिभाषा दीजिए तथा इसकी विमा लिखिए। (2012, 17)
उत्तर-
वैद्युत-विभव-वैद्युत- क्षेत्र में किसी बिन्दु पर वैद्युत-विभव (V), परीक्षण-आवेश (+q₀) को अनन्त से उस बिन्दु तक लाने में किये गये कार्य (W) तथा परीक्षण-आवेश के मान की निष्पत्ति के बराबर होता है।

प्रश्न 2.
इलेक्ट्रॉन-वोल्ट की परिभाषा दीजिए।
या
eV क्या है? इसका मान जूल में ज्ञात कीजिए।
उत्तर-
इलेक्ट्रॉन-वोल्ट- यह ऊर्जा का जूल की तुलना में बहुत छोटा मात्रक है। इसको इस प्रकार परिभाषित किया जाता है-
“1 इलेक्ट्रॉन-बोल्ट (eV) वह ऊर्जा है जो कि 1 इलेक्ट्रॉन (आवेश q = e = 1.6 x 10^-19 कूलॉम) 1 वोल्ट विभवान्तर पर त्वरित होने पर प्राप्त करता है।”
यदि q कूलॉम आवेश से आवेशित कण ΔV विभवान्तर पर त्वरित होता है तो उसके द्वारा प्राप्त गतिज ऊर्जा K = q x ΔV
यहाँ, q = e = 1.6 x 10^-19 कूलॉम तथा V = 1 वोल्ट
1 इलेक्ट्रॉन-वोल्ट ऊर्जा = 1.6 x 10^-19 कूलॉम x 1 वोल्ट = 1.6 x 10^-19 जूल।
इस प्रकार 1 eV = 1.6 x 10^-19 जूल

प्रश्न 3.
1 Mev को जूल में व्यक्त कीजिए।
हल-
1 MeV = 106 eV= 10⁶ x 1.6 x 10^-19 जूल = 1.6 x 10^-13 जूल

प्रश्न 4.
क्या यह सम्भव है कि किसी बिन्दु पर वैद्युत विभव शून्य हो, लेकिन वैद्युत क्षेत्र शून्य न हो?
उत्तर-
हाँ। उदाहरण के लिए, वैद्युत द्विध्रुव की निरक्षीय स्थिति में।

प्रश्न 5.
1 सेमी त्रिज्या के गोले को 1 कूलॉम आवेश देने से गोले के पृष्ठ पर उत्पन्न विभव की गणना कीजिए। (2016)

प्रश्न 6.
+ 40 माइक्रोकूलॉम के दो आवेश परस्पर 0.4 मीटर की दूरी पर स्थित हैं। इनके मध्य बिन्दु पर विभव की गणना कीजिए। माध्यम का परावैद्युतांक 2 है। (2014)
हल-
+ 40 माइक्रोकूलॉम के दोनों आवेशों के कारण उनके मध्य बिन्दु पर वैद्युत विभव

प्रश्न 7.
विभव-प्रवणता तथा वैद्युत क्षेत्र की तीव्रता में सम्बन्ध बताइए।
उत्तर-
वैद्युत क्षेत्र की तीव्रता E = – विभव प्रवणता = $\frac { \triangle V }{ \triangle x }$

प्रश्न 8.
विभव-प्रवणता का मात्रक एवं विमीय सूत्र लिखिए।
उत्तर-
मात्रक-वोल्ट/मीटर तथा विमा- [MLT^-3A^-1]

प्रश्न 9.
दो बिन्दुओं के बीच विभवान्तर 50 V है। एक बिन्दु से दूसरे बिन्दु तक 2 x 10^-5 कूलॉम आवेश को ले जाने पर कितना कार्य करना होगा ? (2011, 12, 18)
हल-
कार्य (W) = आवेश x विभवान्तर = 2 x 10^-5 कूलॉम x 50 वोल्ट = 10^-3 जूल।

प्रश्न 10.
10 सेमी की दूरी पर स्थित दो बिन्दु A व B के विभव क्रमशः +10 वोल्ट तथा -10 वोल्ट हैं। 1.0 कूलॉम आवेश को A से B तक ले जाने में कितना कार्य करना होगा? (2012)
हल-
1.0 कूलॉम आवेश को A से B तक ले जाने में किया गया कार्य
W = (V_B – V_A) q₀ = (-10 – 10) x 1.0 = -20 जूल
अत: कार्य प्राप्त होगा।

प्रश्न 11.
सम-विभव पृष्ठ से क्या तात्पर्य है? (2015, 17)
उत्तर-
किसी वैद्युत क्षेत्र में खींचा गया वह पृष्ठ जिस पर स्थित सभी बिन्दुओं पर वैद्युत विभव बराबर हो, समविभव पृष्ठ कहलाता है।

प्रश्न 12.
किसी समविभव पृष्ठ के दो बिन्दुओं के मध्य 800 μC आवेश को गति कराने में कितना कार्य होगा? (2013)
हल-
समविभव पृष्ठ के प्रत्येक बिन्दु पर विभव का मान समान होता है। अतः पृष्ठ के किन्हीं भी दो बिन्दुओं के बीच विभवान्तर ΔV = 0
अतः q = 800 μC = 800 x 10^-6 कूलॉम को इन बिन्दुओं के बीच गति कराने में किया गया कार्य
W = q x ΔV = (800 x 10^-6) x 0 = 0 (शून्य) [∴ 1 μC = 10^-6 C]

प्रश्न 13.
संधारित्र किसे कहते हैं? (2014)
उत्तर-
संधारित्र एक ऐसा समायोजन है जिसमें किसी चालक के आकार में परिवर्तन किये बिना उस पर आवेश की पर्याप्त मात्रा संचित की जा सकती है।

प्रश्न 14.
संधारित्र की धारिता की परिभाषा लिखिए। (2014, 15)
उत्तर-
किसी संधारित्र की धारिता, उसकी एक प्लेट को दिए गए आवेश तथा दोनों प्लेटों के बीच उत्पन्न विभवान्तर के अनुपात के बराबर होती है।
अर्थात् संधारित्र की धारिता C = $\frac { q }{ V }$

प्रश्न 15.
M.K.S. पद्धति में धारिता की विमा लिखिए। इसका मात्रक क्या है?
उत्तर-
धारिता की विमा [M^-1L^-2T⁴A²] तथा मात्रक फैरड है।

प्रश्न 16.
परावैद्युत पदार्थ क्या है? (2010, 12)
उत्तर-
परावैद्युत पदार्थ वह पदार्थ होता है जिसके अन्दर सभी परमाणुओं में उनके सभी इलेक्ट्रॉन नाभिक के आकर्षण बल से दृढ़तापूर्वक बँधे रहते हैं। अतः ऐसे पदार्थों में वैद्युत चालन के लिए कोई भी मुक्त इलेक्ट्रॉन उपलब्ध नहीं होता अथवा मुक्त इलेक्ट्रॉनों की संख्या नगण्य होती है। अतः परावैद्युत पदार्थ वे पदार्थ हैं जिनमें होकर वैद्युत प्रवाह नहीं होता। फिर भी यदि कोई वैद्युत-क्षेत्र किसी परावैद्युत पदार्थ पर आरोपित किया जाता है तो परावैद्युत पदार्थ के पृष्ठों पर प्रेरित आवेश उत्पन्न हो जाता है। अतः परावैद्युत पदार्थ वे कुचालक (insulator) पदार्थ हैं जिनमें वैद्युत प्रभाव (electric effects) बिना वैद्युत चालन के संचरित होते हैं।” किसी वैद्युत चालक के किसी बिन्दु पर दिया गया आवेश उसकी पूरी सतह पर शीघ्रता से फैल जाता है, जबकि किसी परावैद्युत के किसी बिन्दु पर दिया गया आवेश उसी के निकटवर्ती क्षेत्र में स्थिर रहता है। उदाहरण-काँच, रबर, प्लास्टिक, ऐबोनाइट, माइका, मोम, कागज, लकड़ी आदि।

प्रश्न 17.
संधारित्र में साधारणतया प्रयुक्त होने वाले किन्हीं दो परावैद्युत पदार्थों के नाम लिखिए।
उत्तर-
अभ्रक व काँच।

प्रश्न 18.
किसी परावैद्युत पदार्थ के वैद्युत ध्रुवण से क्या तात्पर्य है?
उत्तर-
द्युत धुवण- किसी परावैद्युत अथवा विद्युतरोधी को बाह्य वैद्युत क्षेत्र में रखने पर इसके धन व ऋण आवेशों के केन्द्र पृथक्-पृथक् हो जाते हैं, जिससे इनमें वैद्युत द्विध्रुव आघूर्ण प्रेरित हो जाते हैं। ऐसे परावैद्युत को ध्रुवित होना कहते हैं तथा इस घटना को वैद्युत ध्रुवण कहते हैं।

प्रश्न 19.
संधारित्रों में परावैद्युत के उपयोग से धारिता क्यों बढ़ जाती है? (2010, 11)
या
किसी संधारित्र की प्लेटों के बीच परावैद्युत पदार्थ भरने पर इसकी धारिता पर क्या प्रभाव पड़ता है? (2014)
उत्तर-
संधारित्रों की प्लेटों के बीच परावैद्युत भरने से इसके अन्दर प्लेटों के बीच उपस्थित वैद्युत-क्षेत्र के विपरीत दिशा में एक आन्तरिक वैद्युत-क्षेत्र उत्पन्न हो जाता है, जो इसकी सतह पर प्लेटों के विपरीत आवेश के प्रेरित होने से उत्पन्न होता है। अतः प्लेटों के बीच विभवान्तर घट जाता है, जिसके परिणामस्वरूप धारिता बढ़ जाती है।

प्रश्न 20.
परावैद्युत सामर्थ्य एवं भंजक विभवान्तर को स्पष्ट कीजिए। (2013).
उत्तर-

परावैद्युत सामर्थ्य- परावैद्युत पर आरोपित वैद्युत-क्षेत्र की तीव्रता का वह अधिकतम मान जिसको परावैद्युत बिना परावैद्युत भंजन के सहन कर सकता है, परावैद्युत की परावैद्युत सामर्थ्य कहलाती है।
भंजक विभवान्तर- किसी परावैद्युत पदार्थ के भंजक हुए बिना उसके दोनों सिरों के बीच लगाए गए वैद्युत विभवान्तर के अधिकतम मान को उस परावैद्युत का भंजक विभवान्तर कहते हैं।

प्रश्न 21.
एक आवेशित संधारित्र एवं एक वैद्युत सेल में मूल अन्तर क्या है? (2009)
उत्तर-
आवेशित संधारित्र में वैद्युत आवेश संग्रहीत रहता है, जबकि वैद्युत सेल में वैद्युत आवेश का प्रवाह होता है।

प्रश्न 22.
समान्तर प्लेट संधारित्र की धारिता के लिए व्यंजक लिखिए तथा प्रतीकों का अर्थ बताइए। (2007)
उत्तर-
C = $\frac { { \varepsilon }_{ 0 }A }{ d }$
A = प्रत्येक प्लेट का क्षेत्रफल,
d = प्लेटों के बीच की दूरी तथा
${ \varepsilon }_{ 0 }$ = वायु या निर्वात् की वैद्युतशीलता।

प्रश्न 23.
दो संधारित्र जिनकी धारिताएँ क्रमशः 20 तथा 30 μF हैं, श्रेणीक्रम में जुड़े हैं। उनकी तुल्य धारिता ज्ञात कीजिए। (2011)
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance VSAQ 23

प्रश्न 24.
नीचे दिये गये परिपथ में A और B बिन्दुओं के बीच तुल्य धारिता ज्ञात कीजिए- (2015)

हल-
दिये गये परिपथ को निम्नांकित चित्र से प्रतिस्थापित कर सकते हैं

स्पष्ट है कि दिया गया परिपथ व्हीटस्टोन सेतु व्यवस्था है, अतः 8 μF पर कोई आवेश संचित नहीं होगा।
अतः चित्र 2.22 को चित्र 2.23 से प्रतिस्थापित किया जा सकता है।
अत: A व B के बीच तुल्य धारिता C = 2 μF + 2 μF = 4 μF

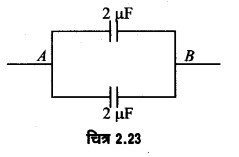
प्रश्न 25.
एक समान्तर प्लेट वायु संधारित्र की धारिता 100 μF है। यदि इसे 50 वोल्ट तक आवेशित किया जाए, तो इसमें संचित ऊर्जा कितनी होगी? (2009)
हल-

प्रश्न 26.
एक 10 μF के संधारित्र का विभवान्तर 100 वोल्ट से 200 वोल्ट कर देने पर उसकी ऊर्जा में परिवर्तन ज्ञात कीजिए। (2011, 12, 14)
हल-
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance VSAQ 26

लघु उत्तरीय प्रश्न

प्रश्न 1.
किसी वैद्युत-क्षेत्र की तीव्रता तथा विभव-प्रवणता के बीच सम्बन्ध स्थापित कीजिए। (2011)
या
विभव-प्रवणता से क्या तात्पर्य है ? विभव-प्रवणता एवं विद्युत-क्षेत्र की तीव्रता के मध्य सम्बन्ध स्थापित कीजिए। (2012)
या
विभव-प्रवणता से आप क्या समझते हैं ? (2018)
उत्तर-
माना बिन्दु O पर स्थित +q आवेश के वैद्युत-क्षेत्र में, जिसकी तीव्रता $\overrightarrow { E }$ है, O से क्रमशः ॐ तथा (x + Δx) दूरी पर x-अक्ष की धनात्मक दिशा में स्थित बिन्दु A तथा बिन्दु B हैं। यदि एक परीक्षण धनावेश +qo बिन्दु B पर रख दिया जाये तो इस आवेश पर इस वैद्युत-क्षेत्र के कारण लगने वाला वैद्युत बल F = q₀E होगा। इस बल की दिशा $\overrightarrow { E }$ की दिशा में अर्थात् X-अक्ष की धनात्मक दिशा में होगी। अत: +q₀ आवेश को बिन्दु B से बिन्दु A तक बल $\overrightarrow { E }$ के विरुद्ध ले जाया गया है। बिन्दु A, बिन्दु O से x दूरी पर स्थित है, अत: इस प्रक्रिया में बाह्य कर्ता को बल $\overrightarrow { F }$ के विरुद्ध कार्य करना पड़ेगा। अत: यदि यह कार्य ΔW हो तो

राशि $\frac { \triangle V }{ \triangle x }$ , दूरी के साथ विभव-परिवर्तन की दर है तथा इसे ही विभव-प्रवणता कहते हैं। अतः किसी वैद्युत-क्षेत्र में किसी बिन्दु पर किसी दिशा में वैद्युत-क्षेत्र की तीव्रता उस दिशा में क्षेत्र की । ऋणात्मक विभव-प्रवणता के बराबर होती है। प्राप्त समीकरण (2). में ऋणात्मक चिह्न यह दर्शाता है कि वैद्युत-क्षेत्र की दिशा में विभव घटता है तथा : वैद्युत-क्षेत्र की तीव्रता की दिशा विभव-प्रवणता की दिशा के विपरीत होती है।

प्रश्न 2.
किसी वैद्युत-द्विध्रुव के अक्ष (अनुदैर्ध्य स्थिति) पर स्थित किसी बिन्दु पर वैद्युत-विभव का सूत्र स्थापित कीजिए। (2011, 17)
या
वैद्युत-द्विध्रुव को परिभाषित कीजिए। किसी वैद्युत-द्विध्रुव की अक्षीय स्थिति में किसी बिन्दु पर वैद्युत विभव का सूत्र स्थापित कीजिए। (2012, 14, 15, 16, 18)
उत्तर-
वैद्युत-द्विधुव- कम दूरी पर स्थित दो बराबर तथा विपरीत आवेशों के निकाय को वैद्युत-द्विध्रुव कहते हैं।
वैद्युत-द्विध्रुव के अक्ष पर स्थित किसी बिन्दु पर वैद्युत- विभव-माना K परावैद्युतांक वाले माध्यम में एक वैद्युत-द्विध्रुव AB रखा है। द्विध्रुव +q व -q कूलॉम के आवेशों से बना है जिनके बीच की दूरी 2l है। द्विध्रुव के मध्य बिन्दु O से r मीटर की दूरी पर इसकी अक्षीय स्थिति में बिन्दु P पर वैद्युत-विभव ज्ञात करना है। चित्र 2.25 से स्पष्ट है कि बिन्दु P की आवेश +q से दूरी (r – l) तथा -q से (r + l) हैं।
आवेश +q के कारण P पर विभव,

प्रश्न 3.
सिद्ध कीजिए कि निरक्षीय स्थिति में किसी बिन्दु पर वैद्युत-द्विध्रुव द्वारा वैद्युत-विभव शून्य होता है। (2010, 15, 16)
उत्तर-
वैद्युत-द्विध्रुव की निरक्षीय स्थिति में वैद्युत-विभव- माना वैद्युत-द्विध्रुव AB की लम्ब-अर्द्धक रेखा पर द्विध्रुव के मध्य-बिन्दु O से r मीटर की दूरी पर स्थित बिन्दु P वह बिन्दु है, जहाँ हमें वैद्युत-विभव ज्ञात करना है। (चित्र 2.26)। अब बिन्दु P पर द्विध्रुव के आवेश (+q) के कारण विभव
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance SAQ 3

प्रश्न 4.
दिये गये आवेशों के निकाय की कुल वैद्युत स्थितिज ऊर्जा ज्ञात कीजिए। (2014)

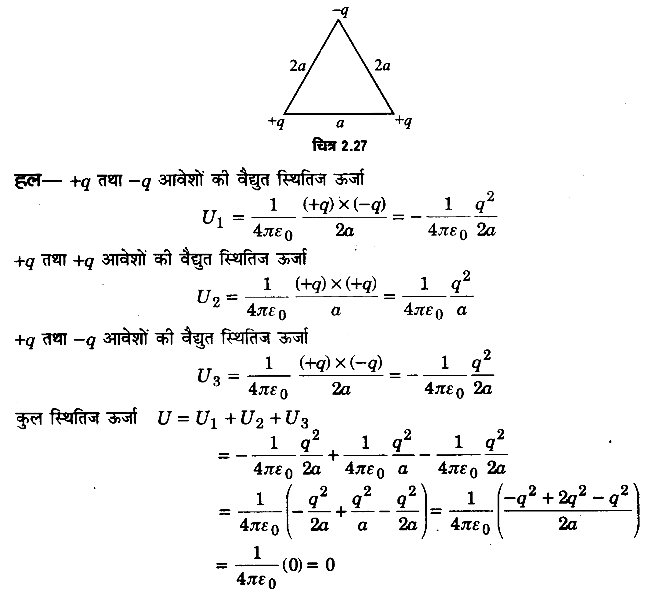
प्रश्न 5.
निम्न चित्र में विभवान्तर (V_A – V_B) के मान की गणना कीजिए- (2016)
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance SAQ 5

प्रश्न 6.
किसी वैद्युत द्विध्रुव को एकसमान विद्युत क्षेत्र में संतुलन की स्थिति से कोण घुमाने में किये गये कार्य का सूत्र प्राप्त कीजिए। (2017)
हल-
माना p वैद्युत-द्विध्रुव आघूर्ण का एक वैद्युत-द्विध्रुव, किसी एकसमान वैद्युत क्षेत्र E में रखा है तथा वैद्युत द्विध्रुव को वैद्युत क्षेत्र के भीतर घुमाया जा रहा है (चित्र 2.29)। माना किसी क्षण वैद्युत-द्विध्रुव आघूर्ण p की दिशा क्षेत्र की दिशा से α कोण बनाती है, तब वैद्युत-द्विध्रुव पर वैद्युत-क्षेत्र के कारण कार्य करने वाले बल-युग्म का आघूर्ण
τ = pE sin α
वैद्युत-द्विध्रुव को इस स्थिति से आगे अल्पांश कोण dα द्वारा घुमाने में वैद्युत-क्षेत्र के विरुद्ध कृत कार्य
dW = बल-युग्म का आघूर्ण x कोणीय विस्थापन
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance SAQ 6

प्रश्न 7.
किसी आवेशित चालक की स्थितिज ऊर्जा के लिए व्यंजक U = $\frac { 1 }{ 2 }$ CV²
अथवा $\frac { 1 }{ 2 } \left( \frac { { q }^{ 2 } }{ C } \right)$ प्त कीजिए, जहाँ C चालक की धारिता, q चालक पर आवेशं तथा V उसका विभव है। (2011, 16)
या
सिद्ध कीजिए कि E , जहाँ E = $\frac { 1 }{ 2 } \left( \frac { { q }^{ 2 } }{ C } \right)$ आवेशित चालक की ऊर्जा, q = चालक
पर आवेश तथा C उसकी धारिता है। या सिद्ध कीजिए कि आवेशित संधारित्र की स्थितिज ऊर्जा U = $\frac { 1 }{ 2 }$ CV² होती है। (2017)
उत्तर-
आवेशित चालक की स्थितिज ऊर्जा- किसी चालक को आवेशित करने में किया गया कार्य उसमें वैद्युत-स्थितिज ऊर्जा के रूप में संचित हो जाता है। चूंकि प्रारम्भ में चालक पर आवेश शून्य है; अतः चालक तल पर विभव भी शून्य होगा। जैसे-जैसे चालक को आवेश दिया जाता है, उसका विभव वैसे-वैसे बढ़ता जाता है, क्योंकि चालक का विभव उसे पर उपस्थित आवेश के अनुक्रमानुपाती होता है। माना चालक को कुल आवेश q कूलॉम देने पर उसका विभव V वोल्ट (बैटरी के विभव के बराबर) हो जाता है। हम यह मान सकते हैं कि चालक को आवेश देते समय उसका औसत विभव (0 + V) / 2 = V/2 रहा; अतः चालक को आवेशित करने में किया गया कुल कार्य

प्रश्न 8.
एक समान्तर प्लेट संधारित्र को बैटरी से आवेशित किया जाता है। बैटरी का सम्बन्ध संधारित्र से विच्छेदित करने के उपरान्त प्लेटों के बीच की दूरी दोगुनी करने पर संधारित्र की धारिता तथा संग्रहित ऊर्जा पर क्या प्रभाव पड़ेगा? (2011)
उत्तर-
माना कि संधारित्र पर संचित आवेश q है।

प्रश्न 9.
किसी चालक की वैद्युत धारिता से क्या तात्पर्य है ? RC का विमीय समीकरण निकालिए, जहाँ प्रतिरोध तथा C धारिता है। (2011)
उत्तर-
किसी चालक की वैद्युत धारिता- किसी चालक द्वारा आवेश ग्रहण करने की क्षमता उसकी वैद्युत धारिता कहलाती है। यह चालक को दिये गये आवेश तथा उसके संगत विभव में होने वाली वृद्धि के अनुपात के बराबर होती है।
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance SAQ 9

प्रश्न 10.
संधारित्र के ऊर्जा घनत्व से क्या तात्पर्य है? प्रदर्शित कीजिए कि एकांक आयतन में किसी समानान्तर प्लेट संधारित्र में संचित ऊर्जा, $\frac { 1 }{ 2 } { \varepsilon }_{ 0 }{ E }^{ 2 }$ है, जहाँ प्रतीकों का सामान्य अर्थ है। (2011, 15, 17)
उत्तर-
आवेशित संधारित्र की ऊर्जा उसकी प्लेटों के बीच स्थित माध्यम में निहित रहती है। संधारित्र की प्लेटों द्वारा घेरे गये माध्यम के एकांक आयतन में निहित ऊर्जा को संधारित्र का ऊर्जा घनत्व कहते हैं। अतः संधारित्र का ऊर्जा घनत्व

प्रश्न 11.
तीन संधारित्र C₁, C₂ और C₃ श्रेणीक्रम में जुड़े हैं। इनकी समतुल्य धारिता का व्यंजक प्राप्त कीजिए। (2015, 17)

UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance SAQ 11.1

प्रश्न 12.
एक समान्तर प्लेट संधारित्र की प्लेटों का व्यास 8 सेमी है। प्लेटों के बीच वायु भरी है। यदि इस संधारित्र की धारिता 100 सेमी त्रिज्या के गोले की धारिता के बराबर हो, तो इसकी प्लेटों के बीच दूरी की गणना कीजिए। (2014)
हल-
समान्तर प्लेट संधारित्र की धारिता = 100 सेमी त्रिज्या वाले गोले की धारिता

प्रश्न 13.
100 μF समान्तर प्लेट संधारित्र 400 वोल्ट तक आवेशित है। यदि इसके प्लेटों के बीच दूरी आधी कर दें तो प्लेटों के बीच नया विभवान्तर क्या होगा और संचित ऊर्जा में क्या परिवर्तन होगा ? (2014)

प्रश्न 14.
दिये गये परिपथ में यदि A तथा B बिन्दुओं के बीच 150 वोल्ट विभवान्तर लगाया जाये तो 6 μF के संधारित्र के प्लेटों के बीच उत्पन्न विभवान्तर एवं संचित ऊर्जा की गणना कीजिए। (2015)

प्रश्न 15.
संधारित्रों के दिये गये नेटवर्क में बिन्दुओं A और B के बीच तुल्य धारिता ज्ञात कीजिए और 4 μF संधारित्र के प्लेटों के बीच विभवान्तर की गणना कीजिए। (2016)

हल-
चित्र 2.32 में 3 μF, 3 μF तथा 3 μF समान्तर क्रम में हैं। अत: इनकी तुल्य धारिता यदि C₁ हो, तो।
C₁ = 3 + 3 + 3 = 9 μF
तथा 18 μF एवं C = 9 μF श्रेणीक्रम में हैं।
अतः इनकी तुल्य धारिता यदि C₂ हो, तो

प्रश्न 16.
वैद्युत संधारित्र क्या होते हैं? इनके किन्हीं दो उपयोगों का उल्लेख कीजिए। धातु के दो गोलों की त्रिज्याएँ 18 सेमी तथा 27 सेमी हैं। प्रत्येक को 75 माइक्रोकूलॉम आवेश दिया गया है। चालक द्वारा दोनों गोलों को जोड़ने पर उभयनिष्ठ विभव का मान ज्ञात कीजिए। (2016)
उत्तर-
वैद्युत संधारित्र- वैद्युत संधारित्र एक ऐसा समायोजन है जिसमें किसी चालक के आकार में परिवर्तन किए बिना उस पर आवेश की पर्याप्त मात्रा संचित की जा सकती है। माना कि किसी चालक को q आवेश देने पर उसका वैद्युत विभव V हो जाता है, तब चालक की धारिता, C = $\frac { q }{ V }$
संधारित्रों के उपयोग- संधारित्रों के प्रमुख उपयोग निम्नवत् हैं-

1. आवेश का संचय करने में संधारित्र को मुख्यत: आवेश का संचय करने में उपयोग किया जाता है। किसी परिपथ में क्षणिक एवं प्रबल धारी प्राप्त करने के लिए उस परिपथ में एक आवेशित संधारित्र जोड़ दिया जाता है। क्षणिक एवं शक्तिशाली चुम्बकीय क्षेत्र उत्पन्न करने के लिए स्पन्दित वैद्युत चुम्बक (pulsed electromagnet) का प्रयोग करते हैं जो किसी आवेशित संधारित्र से ही प्रबल धारा प्राप्त करते हैं।

2. ऊर्जा का संचय करने में-आवेशित संधारित्र की प्लेटों के बीच वैद्युत क्षेत्र में पर्याप्त वैद्युत स्थितिज ऊर्जा संचित रहती है। यदि संख्या में बहुत अधिक आवेशित संधारित्रों का एक स्थिरवैद्युत विभव तथा धारिता 93 संयोजन (संधारित्र बैंक) बनाएँ तो उस ऊर्जा की बड़ी मात्रा को संचित किया जा सकता है और समय आने पर उससे आवश्यकतानुसार ऊर्जा प्राप्त की जा सकती है।

3. इलेक्ट्रॉनिक परिपथों में इलेक्ट्रॉनिक परिपथों में विभिन्न कार्यों के लिए संधारित्रों का प्रयोग किया जाता है। उदाहरण के लिए, रेडियो-आवृत्ति के वैद्युत चुम्बकीय दोलनों के उत्पादन एवं संसूचन में अर्थात् रेडियो, टेलीविजन इत्यादि के कार्यक्रमों के प्रसारण तथा अभिग्रहण में, वैद्युत शक्ति-सम्भरण (electric power supply) में वोल्टता के उच्चावचन (fluctuations) कम करने में प्रायः फिल्टर प्रयोग होते हैं और संधारित्र एकदिशीय धारा के स्पन्दनों (pulses) के आयाम को कम करके दिष्ट धारा प्राप्त कराने में सहायक होता है।

4. वैद्युत उपकरणों में—वैद्युत उपकरणों जैसे-प्रेरण कुण्डली (induction coil), मोटर इंजन के ज्वलन तन्त्र (ignition system), बिजली के पंखे इत्यादि में संधारित्रों का उपयोग किया जाता है। हम जानते हैं कि जब किसी प्रेरकीय परिपथ को अचानक तोड़ा जाता है, तो उस स्थान पर चिंगारी (spark) उत्पन्न होती है, परन्तु यदि उसे परिपथ में संधारित्र को लगाया गया है, तो परिपथ के टूटने से उत्पन्न प्रेरित धारा संधारित्र की प्लेटों को आवेशित कर चिंगारी उत्पन्न होने की सम्भावना को समाप्त कर देती है।

5. वैज्ञानिक अध्ययन में-वैज्ञानिक अध्ययनों में भी संधारित्रों का विशेष महत्त्व है। विभिन्न प्रकार के संधारित्रों में विभिन्न आकार की प्लेटों के बीच अलग-अलग विन्यासों (configurations) के वैद्युत क्षेत्र स्थापित कर उसमें विभिन्न परावैद्युत पदार्थों को रखकर वैद्युत क्षेत्र में उनके वैद्युत व्यवहारों का अध्ययन किया जाता है।
दिया है, गोलों की त्रिज्याएँ 0.18 मीटर तथा 0.27 मीटर हैं। a मीटर त्रिज्या के गोले की धारिता

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
वैद्युत विभव की परिभाषा लिखिए। वैद्युत-आवेश के कारण किसी बिन्दु पर वैद्युत विभव के लिए व्यंजक प्राप्त कीजिए। (2015)
उत्तर-
वैद्युत-विभव वैद्युत- क्षेत्र में किसी बिन्दु पर वैद्युत-विभव (V) परीक्षण आवेश (+q₀) को अनन्त से उस बिन्दु तक लाने में किये गये कार्य (W) तथा परीक्षण-आवेश के मान की निष्पत्ति के बराबर होता है।

UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance LAQ 1.1

प्रश्न 2.
समान्तर-प्लेट संधारित्र की धारिता के लिए व्यंजक का निगमन कीजिए। इसकी धारिता को कैसे बढ़ाया जा सकता है। (2013, 15, 16, 17)
या
किसी समान्तर-पट्ट संधारित्र की धारिता का व्यंजक प्राप्त कीजिए, जबकि दोनों प्लेटों के बीच परावैद्युत भरा हो। (2013)
या
किसी समान्तर-प्लेट संधारित्र की धारिता के लिए व्यंजक प्राप्त कीजिए। (2011, 14)
या
किसी समतल आवेशित प्लेट के निकट वैद्युत-क्षेत्र की तीव्रता का सूत्र लिखिए। इसका उपयोग करके समान्तर-प्लेट संधारित्र की धारिता के व्यंजक का निगमन कीजिए। (2011)
उत्तर-
समान्तर-प्लेट संधारित्र की धारिता- चित्र 2.34 में एक समान्तर-प्लेट संधारित्र दिखाया। गया है जिसमें मुख्यत: धातु की लम्बी व समतल दो प्लेटें Xव Y होती हैं जो एक-दूसरे के आमने-सामने थोड़ी दूरी पर दो विद्युतरोधी स्टैण्डों में लगी रहती हैं। इन समान्तर-प्लेटों के बीच वायु के स्थान पर कोई विद्युतरोधी माध्यम (परावैद्युतांक K) भरा है। समतल प्लेटों में से प्रत्येक का क्षेत्रफल A मीटर तथा उनके बीच की दूरी d मीटर है।

जब प्लेट X को +q आवेश दिया जाता है तो प्रेरण के कारण प्लेट Y पर अन्दर की ओर -q आवेश तथा बाहर की ओर +q आवेश उत्पन्न हो जाता है, चूंकि प्लेंट Y पृथ्वी से जुड़ी है; अतः इसके बाहरी तल का +q आवेश पृथ्वी में चला जाएगा। अंतः प्लेटों के बीच वैद्युत-क्षेत्र उत्पन्न हो जाएगा और लगभग सभी जगह क्षेत्र की तीव्रता एकसमान होगी।
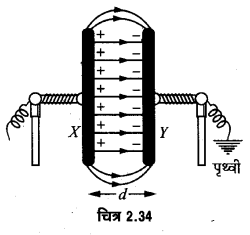
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance LAQ 2

समान्तर प्लेट संधारित्र की धारिता को निम्नलिखित प्रकार से बढ़ाया जा सकता है-

प्रयुक्त प्लेटें अधिक क्षेत्रफल की होनी चाहिए।
प्लेटों के बीच ऐसा माध्यम रखना चाहिए जिसका परावैद्युतांक अधिक हो।
प्लेटों के बीच की दूरी (d) कम लेनी चाहिए अर्थात् प्लेटें परस्पर समीप रखनी चाहिए।

प्रश्न 3.
समान धारिता के चार संधारित्र समान्तर-क्रम में जुड़े हैं। 1.5 वोल्ट की बैटरी से जोड़ने पर प्रत्येक संधारित्र पर संचित आवेश 1.5 माइक्रोकूलॉम है। यदि इन्हें श्रेणीक्रम में जोड़कर उसी बैटरी से आवेशित किया जाए, तो प्रत्येक संधारित्र पर संचित आवेश की गणना कीजिए। (2016)

प्रश्न 4.
एक समान्तर प्लेट वायु संधारित्र की धारिता 2 μF है। जब इसकी प्लेटों के बीच, प्लेटों के बीच की दूरी की तीन-चौथाई मोटाई की k परावैद्युतांक की प्लेट रखी जाती है, तब संधारित्र की धारिता 4 μF हो जाती है। k का मान ज्ञात कीजिए जहाँ प्लेटों का तथा परावैद्युत प्लेट का क्षेत्रफल समान है। (2014)
हल-
माना प्लेट का क्षेत्रफल = A
प्लेटों के बीच की दूरी = d

प्रश्न 5.
दिये गये चित्र 2.35 में A और B बिन्दुओं के बीच तुल्यधारिता ज्ञात कीजिए। (2012)

प्रश्न 6.
एक समान्तर प्लेट संधारित्र की प्रत्येक प्लेट का क्षेत्रफल 40 सेमी है तथा दोनों प्लेटों के बीच विद्युत-क्षेत्र की तीव्रता 50 न्यूटन प्रति कूलॉम है। प्रत्येक प्लेट पर आवेश की गणना कीजिए। (2014)
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance LAQ 6

प्रश्न 7.
दिए गए परिपथ में संधारित्र की वैद्युत स्थितिज ऊर्जा की गणना कीजिए। (2013)
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance LAQ 7

प्रश्न 8.
दिए गए परिपथ में दोनों संधारित्रों पर संचित आवेशों की गणना कीजिए।

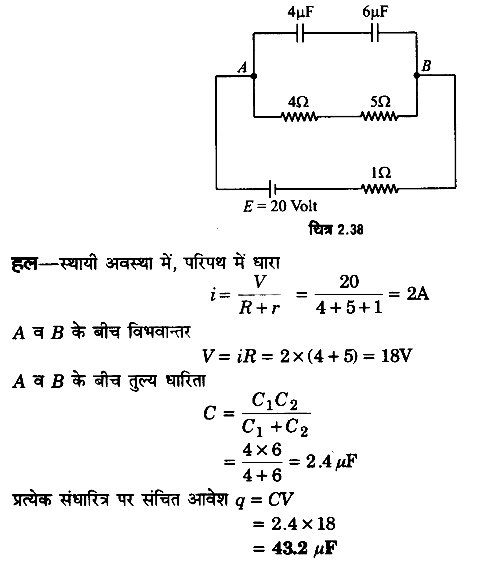
प्रश्न 9.
वानडे ग्राफ जनित्र की संरचना तथा कार्यविधि चित्र की सहायता से समझाइए। (2015)
या
वानडे ग्राफ जनित्र के सिद्धान्त एवं कार्यविधि का वर्णन कीजिए। (2017)
या
वानडे ग्राफ जनित्र के गुण-दोष/उपयोग का वर्णन कीजिए।
या
वानडे ग्राफ जनित्र का नामांकित चित्र बनाइए। इसके कार्य करने का सिद्धान्त बताइए। यह किस तरह से उच्च वोल्टेज उत्पन्न करता है? (2018)
उत्तर-
प्रोफेसर वानडे ग्राफ ने सन् 1931 में एक ऐसे स्थिर वैद्युत उत्पादक यन्त्र (electrostatic generator) की रचना की जिसके द्वारा दस लाख वोल्ट या इससे भी उच्च कोटि का विभवान्तर उत्पन्न किया जा सकता है। इस जनित्र को उनके नाम पर ही वानडे ग्राफ जनित्र कहते हैं।

सिद्धान्त-
इस जनित्र का सिद्धान्त निम्न दो स्थिर वैद्युत घटनाओं पर आधारित है-
(i) एक खोखले चालक का आवेश उसकी बाहरी सतह पर विद्यमान रहता है।
(ii) किसी चालक से वायु में वैद्युत विसर्जन, उसके नुकीले सिरों की प्राथमिकता से होता है। इस जनित्र की कार्यविधि वैद्युत चालक के नुकीले सिरों (pointed ends) की क्रिया पर आधारित है। चालक के नुकीले भाग पर आवेश का पृष्ठ घनत्व बहुत अधिक होने के कारण, इसे भाग के पास तीव्र वैद्युत क्षेत्र उपस्थित होता है, जिससे वहाँ भी वायु का आयनीकरण (ionisation) हो जाता है। तब विपरीत प्रकृति का आवेश आकर्षण के कारण नुकीले भाग के पास तथा समान प्रकृति का आवेश प्रतिकर्षण के कारण नुकीले भाग से दूर की ओर दौड़ता है अर्थात् नुकीले भाग से वैद्युत पवन उत्पन्न हो जाता है।

यदि किसी खोखले चालक गोले के अन्दर जुड़े किसी चालक के (नुकीले भाग के) पास कोई आवेश लाया जाए, तो यह सम्पूर्ण आवेश खोखले चालक के बाहरी पृष्ठ पर स्थानान्तरित हो जाता है, चाहे खोखले चालक को विभव कितना भी अधिक हो। इस प्रकार खोखले चालक पर बार-बार आवेश देकर इसके आवेश तथा विभव को बहुत अधिक मान तक बढ़ाया जा सकता है। इसकी सीमा वैद्युतरोधी कठिनाइयों द्वारा निर्धारित की जाती है।

रचना-
चित्र 2.39 में वानडे ग्राफ जनित्र की रचना प्रदर्शित है। इसमें लगभग 5 मीटर व्यास के धातु का खोखला गोला S होता है जो लगभग 15 मीटर ऊँचे विद्युतरोधी स्तम्भों A व B पर टिका रहता है। P₁ और P₂ दो घिरनियाँ होती हैं जिनमें से होकर विद्युतरोधी पदार्थ; जैसे-रबर या रेशम की बनी एक पट्टी (belt) गुजरती है।

नीचे की घिरनी P को एक वैद्युत मोटर के द्वारा घुमाया जाता है जिससे पट्टी ऊध्र्वाधर तल में तीर की दिशा में घूमने लगती है। C₁ और C₂ धातु की दो कंघियाँ होती हैं। C₁ को फुहार कंघी (spray comb) तथा C₂ को संग्राहक कंघी (collection comb) कहते हैं। कंघी C₁ को एक उच्च विभव की बैटरी के धने सिरे से जोड़ दिया जाता है ताकि वह लगभग 10000 वोल्ट के पृथ्वी धनात्मक विभवे पर रह सके। कंघी C₂ को गोले S के हैं आन्तरिक पृष्ठ से जोड़ दिया जाता है। D एक विसर्जन-नलिका (discharge tube) है।

चित्र 2.39 गोले से आवेश के क्षरण (leakage) को रोकने के लिए जनित्र को एक लोहे के टैंक में जिसमें दाब । युक्त (लगभग 15 वायुमण्डलीय दाब) वायु भरी होती है, बन्द कर देते हैं। लोहे का टैंक पृथ्वीकृत होता है।

कार्यविधि-
जब कंघे C₁ को अति उच्च विभव दिया जाता है, तो तीक्ष्ण बिन्दुओं की क्रिया के फलस्वरूप यह इसके स्थान में आयन उत्पन्न करता है। धन आयनों व कंघे C₁ के बीच प्रतिकर्षण के कारण ये धन आयन बेल्ट पर चले जाते हैं। गतिमान बेल्ट द्वारा ये आयन ऊपर ले जाए जाते हैं। C₂ के तीक्ष्ण सिरे बेल्ट को ठीक छूते हैं। इस प्रकार कंघा C₂ बेल्ट के धन आवेश को एकत्रित करता है। यह धन आवेश शीघ्र ही गोले S के बाहरी पृष्ठ पर स्थानान्तरित हो जाता है। चूंकि बेल्ट घूमती रहती है, यह धन आवेश को ऊपर की ओर ले जाती है जो कंघे C₂ द्वारा एकत्रित कर लिया जाता है तथा गोले S के बाहरी पृष्ठ पर स्थानान्तरित हो जाता है। इस प्रकार गोले S का बाहरी पृष्ठ निरन्तर धन आवेश प्राप्त करता है तथा इसका विभवे अति उच्च हो जाती है। जब गोले S का विभवे बहुत अधिक हो जाता है, तो निकटवर्ती वायु की परावैद्युत तीव्रता (dielectric strength) टूट जाती है तथा आवेश का निकटवर्ती वायु में क्षरण (leakage) हो जाता है। अधिकतम विभव की स्थिति में आवेश के क्षरण होने की दर गोले पर स्थानान्तरित आवेश की दर के बराबर हो। जाती है। गोले से आवेश का क्षरण रोकने के लिए, जनित्र को पृथ्वी से सम्बन्धित तथा उच्च दाबे पर वायू भरे टैंक में रखा जाता है।
UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance LAQ 9.1
वास्तविक जनित्र में एक खोखले गोले S के स्थान पर दो खोखले गोले प्रयुक्त करके, एक गोले पर धनावेश तथा दूसरे गोले पर ऋणावेश एकत्रित करके, इन दोनों गोलों के बीच एक अत्यन्त उच्च विभवान्तर प्राप्त कर लिया जाता है।
वानडे ग्राफ जनित्र धन आवेशित कणों को अति उच्च वेग तक त्वरित करने के लिए प्रयोग किया जाता है। इस प्रकार का जनित्र IIT कानपुर में लगा है जो आवेशित कणों को 2 Mev ऊर्जा तक त्वरित करता
उपयोग-
वानडे ग्राफ जनित्र के उपयोग निम्नलिखित हैं

उच्च विभवान्तर उत्पन्न करने के लिए,
तीव्र एक्स किरणों के उत्पादन में,
नाभिकीय विघटन के प्रयोगों में आवेशित कणों (प्रोटॉन, ड्यूट्रॉन तथा α कण आदि) को उच्च गतिज ऊर्जा प्रदान करने में,
नाभिकीय भौतिकी के अध्ययन में इसका उपयोग कण त्वरक (particle accelerator) के रूप में किया जाता है।

दोष-
वानडे ग्राफ जनित्र के दोष निम्नवत् हैं-

इसके आकार के बड़ा होने के कारण इसका उपयोग असुविधाजनक होता है।
उच्च विभव के कारण इसको उपयोग खतरनाक होता है।

We hope the UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance (स्थिरवैद्युत विभव तथा धारिता) help you.

UP Board Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance (स्थिरवैद्युत विभव तथा धारिता)

Leave a Reply Cancel reply