UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism (गतिमान आवेश और चुम्बकत्व)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
तार की एक वृत्ताकार कुंडली में 100 फेरे हैं, प्रत्येक की त्रिज्या 8.0 cm है और इनमें 0.40A विद्युत धारा प्रवाहित हो रही है। कुंडली के केन्द्र पर चुम्बकीय क्षेत्र का परिमाण क्या है ?
हल-
दिया है,
कुण्डली में तार के फेरों की संख्या n = 100
प्रत्येक फेरे की त्रिज्या r = 8.0 सेमी = 8.0 x 10^-2 मीटर
कुण्डली में प्रवाहित धारा I = 0.40 ऐम्पियर
कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का परिमाण B = ?

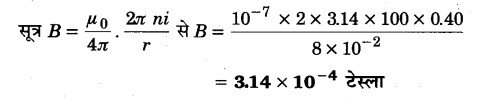
प्रश्न 2.
एक लम्बे, सीधे तार में 35 A विद्युत धारा प्रवाहित हो रही है। तार से 20 cm दूरी पर स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र का परिमाण क्या है?
हल-
एक लम्बी धारावाही सीधी तार के कारण r दूरी पर उत्पन्न चुम्बकीय क्षेत्र,
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q2

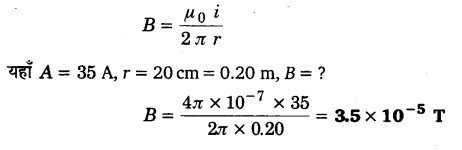
प्रश्न 3.
क्षैतिज तल में रखे एक लम्बे सीधे तार में 50A विद्युत धारा उत्तर से दक्षिण की ओर प्रवाहित हो रही है। तार के पूर्व में 2.5 m दूरी पर स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र B का परिमाण और उसकी दिशा ज्ञात कीजिए।
हल-
दिया है,
धारा की प्रबलता I = 50 ऐम्पियर
दिए गए बिन्दु की तार से लम्बवत् दूरी r = 2.5 मीटर
बिन्दु पर चुम्बकीय क्षेत्र B का परिमाण व दिशा = ?

प्रश्न 4.
व्योमस्थ खिंचे क्षैतिज बिजली के तार में 90 A विद्युत धारा पूर्व से पश्चिम की ओर प्रवाहित हो रही है। तार के 1.5 m नीचे विद्युत धारा के कारण उत्पन्न चुम्बकीय क्षेत्र का परिमाण और दिशा क्या है?
हल-
तार में धारा i = 90 A (पूर्व से पश्चिम), तार से दूरी = 1.5 m
तार के कारण चुम्बकीय क्षेत्र
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q4
चुम्बकीय क्षेत्र की दिशा क्षैतिजत: उत्तर से दक्षिण की ओर होगी।

प्रश्न 5.
एक तार जिसमें 8 A विद्युत धारा प्रवाहित हो रही है, 0.15 T के एकसमान चुम्बकीय क्षेत्र में, क्षेत्र से 30° का कोण बनाते हुए रखा है। इसकी एकांक लम्बाई पर लगने वाले बल का परिमाण और इसकी दिशा क्या है?
हल-
चुम्बकीय क्षेत्र B में क्षेत्र से θ कोण पर रखे L लम्बाई के धारावाही चालक तार पर लगने वाले बल का परिमाण
F = ILB sin θ (जहाँ I = तार में प्रवाहित धारा)
तार की एकांक लम्बाई ( $\frac { F }{ L }$ ) = IB sin θ
यहाँ I = 8A; B = 0.15 T तथा θ = 30°
( $\frac { F }{ L }$ ) = 8 x 0.15 x sin 30° न्यूटन/मीटर
= 8 x 0.15 x ( $\frac { 1 }{ 2 }$ ) न्यूटन/मीटर
= 0.60 न्यूटन/मीटर

प्रश्न 6.
एक 3.0 cm लम्बा तार जिसमें 10 A विद्युत धारा प्रवाहित हो रही है, एक परिनालिका के भीतर उसके अक्ष के लम्बवत् रखा है। परिनालिका के भीतर चुम्बकीय क्षेत्र का मानं 0.27 T है। तार पर लगने वाला चुम्बकीय बल क्या है?
हल-
परिनालिका के अन्दर उसकी अक्ष पर चुम्बकीय क्षेत्र B = 0.27 T (जिसकी दिशा अक्ष के अनुदिश ही होती है)। धारावाही तार अक्ष के लम्बवत् है,
अतः θ = 90°; तार की लम्बाई L = 3.0 सेमी = 3.0 x 10^-2 मी; तार में धारा I = 10 A; अतः तार पर लगने वाला चुम्बकीय बल
F = ILB sin θ न्यूटन
= 10 x (3.0 x 10^-2) (0.27) x sin 90° न्यूटन
= 81 x 10^-2 x 1 न्यूटन
= 8.1 x 10^-2 न्यूटन

प्रश्न 7.
एक-दूसरे से 4.0 cm की दूरी पर रखे दो लम्बे, सीधे, समान्तर तारों A एवं B से क्रमशः 8.0 A एवं 5.0 A की विद्युत धाराएँ एक ही दिशा में प्रवाहित हो रही हैं। तार A के 10 cm खण्ड पर बल का आकलन कीजिए।
हल-
परस्पर समान्तर दो लम्बे सीधे धारावाही तारों के बीच प्रत्येक तार की एकांक लम्बाई पर कार्य करने वाला पारस्परिक बल

प्रश्न 8.
पास-पास फेरों वाली एक परिनालिका 80 cm लम्बी है और इसमें 5 परतें हैं जिनमें से प्रत्येक में 400 फेरे हैं। परिनालिका का व्यास 1.8 cm है। यदि इसमें 8.0 A विद्युत धारा प्रवाहित हो रही है तो परिनालिका के भीतर केन्द्र के पास चुम्बकीय क्षेत्र B का परिमाण परिकलित कीजिए।

प्रश्न 9.
एक वर्गाकार कुंडली जिसकी प्रत्येक भुजा 10 cm है, में 20 फेरे हैं और उसमें 12 A विद्युत धारा प्रवाहित हो रही है। कुंडली ऊर्ध्वाधरतः लटकी हुई है और इसके तल पर खींचा गया अभिलम्ब 0.80 T के एकसमान चुम्बकीय क्षेत्र की दिशा से 30° का एक कोण बनाता है। कुंडली पर लगने वाले बल-युग्म आघूर्ण का परिमाण क्या है?
हल-
बल-युग्म के आघूर्ण का परिमाण τ = NIAB sin θ
यहाँ फेरों की संख्या N = 20; वर्गाकार कुण्डली के तल को क्षेत्रफल
A = भुजा² = (0.10 मी)² = 0.01 मी
कुण्डली में धारा I = 12 A; चुम्बकीय क्षेत्र B = 0.80 T तथा θ = 30°
τ = 20 x 12 x 0.01 x 0.80 x sin 30° न्यूटन मीटर
= 240 x 0.008 x ( $\frac { 1 }{ 2 }$ ) न्यूटन मीटर
= 0.960 न्यूटन मीटर।

प्रश्न 10.
दो चल कुंडली गैल्वेनोमीटर मीटरों MI एवं M, के विवरण नीचे दिए गए हैं।
R₁ = 10 Ω, N₁ = 30, A₁ = 3.6 x 10^-3 m², B₁ = 0.25 T
R₂ = 14 Ω, N₂ = 42, A₂ = 1.8 x 10^-3 m², B₂ = 0.50 T
(दोनों मीटरों के लिए स्प्रिंग नियतांक समान है)।
(a) M₂ एवं M₁ की धारा-सुग्राहिताओं,
(b) M₂ एवं M₁ की वोल्टता-सुग्राहिताओं का अनुपात ज्ञात कीजिए।

प्रश्न 11.
एक प्रकोष्ठ में 6.5 G (1G = 10^-4 T) का एकसमान चुम्बकीय क्षेत्र बनाए रखा गया है। इस चुम्बकीय क्षेत्र में एक इलेक्ट्रॉन 4.8 x 10⁶ ms^-1 के वेग से क्षेत्र के लम्बवत् भेजा गया है। व्याख्या कीजिए कि इस इलेक्ट्रॉन का पथ वृत्ताकार क्यों होगा? वृत्ताकार कक्षा की त्रिज्या ज्ञात कीजिए। (e = 1.6 x 10¹⁹ C, me = 9.1 x 10^-31 kg)
हल-
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q11
क्योंकि चुम्बकीय क्षेत्र में लम्बवत् प्रवेश करने वाले इलेक्ट्रॉन पर चुम्बकीय बल सदैव इसके वेग के लम्बवत् रहने के कारण इलेक्ट्रॉन का पथ वृत्ताकार हो जाता है।

प्रश्न 12.
प्रश्न 11 में, वृत्ताकार कक्षा में इलेक्ट्रॉन की परिक्रमण आवृत्ति प्राप्त कीजिए। क्या यह उत्तर इलेक्ट्रॉन के वेग पर निर्भर करता है? व्याख्या कीजिए।

प्रश्न 13.
(a) 30 फेरों वाली एक वृत्ताकार कुंडली जिसकी त्रिज्या 8.0 cm है और जिसमें 6.0 A विद्युत धारा प्रवाहित हो रही है, 1.0 T के एकसमान क्षैतिज चुम्बकीय क्षेत्र में ऊर्ध्वाधरतः लटकी है। क्षेत्र रेखाएँ कुंडली के अभिलम्ब से 60° का कोण बनाती हैं। कुंडली को घूमने से रोकने के लिए जो प्रति आघूर्ण लगाया जाना चाहिए उसके परिमाण परिकलित कीजिए।
(b) यदि (a) में बतायी गई वृत्ताकार कुंडली को उसी क्षेत्रफल की अनियमित आकृति की समतलीय कुंडली से प्रतिस्थापित कर दिया जाए (शेष सभी विवरण अपरिवर्तित रहें) तो क्या आपका उत्तर परिवर्तित हो जाएगा?
हल-
(a) कुंडली में फेरे N = 30, त्रिज्या r = 8.0 x 10^-2 m, i = 6.0 A
चुम्बकीय क्षेत्र B = 1.0 T, θ = 60°
कुंडली पर चुम्बकीय क्षेत्र के कारण बल-युग्म का आघूर्ण
τ = NiAB sin 60° = Ni (πr²) B sin 60°
= 30 x 6.0 x (314 x 64.0 x 10^-4) x 1.0 x $\frac { \surd 3 }{ 2 }$ = 3.13 N-m
स्पष्ट है कि कुंडली को घूमने से रोकने के लिए 3.13 N-m का बल-आघूर्ण विपरीत दिशा में लगाना होगा।
(b) नहीं, उत्तर में कोई परिवर्तन नहीं होगा। इसका कारण यह है कि बल-आघूर्ण (τ = NiAB sin θ) कुंडली के क्षेत्रफल A पर निर्भर करता है न कि उसके आकार पर।

अतिरिक्त अभ्यास

प्रश्न 14.
दो समकेन्द्रिक वृत्ताकार कुंडलियाँ x और Y जिनकी त्रिज्याएँ क्रमशः 16 cm एवं 10 cm हैं, उत्तर-दक्षिण दिशा में समान ऊध्र्वाधर तल में अवस्थित हैं। कुंडली X में 20 फेरे हैं और इसमें 16 A विद्युत धारा प्रवाहित हो रही है, कुंडली Y में 25 फेरे हैं और इसमें 18 A विद्युत धारा प्रवाहित हो रही है। पश्चिम की ओर मुख करके खड़ा एक प्रेक्षक देखता है कि X में धारा प्रवाह वामावर्त है जबकि में दक्षिणावर्त है। कुंडलियों के केन्द्र पर, उनमें प्रवाहित विद्युत धाराओं के कारण उत्पन्न कुल चुम्बकीय क्षेत्र का परिमाण एवं दिशा ज्ञात कीजिए।

प्रश्न 15.
10 cm लम्बाई और 10^-3 m² अनुप्रस्थ काट के एक क्षेत्र में 100 G (1G = 10^-4) का एकसमान चुम्बकीय क्षेत्र चाहिए। जिस तार से परिनालिका का निर्माण करना है उसमें अधिकतम 15 A विद्युत धारा प्रवाहित हो सकती है और क्रोड पर अधिकतम 1000 फेरे प्रति मीटर लपेटे जा सकते हैं। इस उद्देश्य के लिए परिनालिका के निर्माण का विवरण सुझाइए। यह मान लीजिए कि क्रोड लौह-चुम्बकीय नहीं है।
हल-
माना परिनालिका की एकांक लम्बाई में फेरों की संख्या n तथा उसमें प्रवाहित धारा 1 है तब उसकी अक्ष पर केन्द्रीय भाग में
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q15
दी गई परिनालिका के लिए ni = नियतांक
इस प्रतिबन्ध में दो चर राशियाँ हैं; अत: हम किसी एक राशि को दी गई सीमाओं के अनुरूप स्वेच्छ मान देकर दूसरी राशि का चुनाव कर सकते हैं।
इससे स्पष्ट है कि अभीष्ट परिनालिका के बहुत से भिन्न-भिन्न विवरण सम्भव हैं।

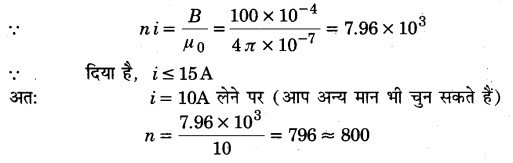
हम जानते हैं कि परिनालिका की अक्ष पर उसके केन्द्रीय भाग में चुम्बकीय क्षेत्र लगभग एकसमान होता है। अतः दिया गया स्थान (10 cm लम्बा व 10^-3 m² अनुप्रस्थ क्षेत्रफल वाला) परिनालिका की अक्ष के अनुदिश तथा केन्द्रीय भाग में होना चाहिए।
अत: परिनालिका की लम्बाई लगभग 50 cm से 100 cm के बीच (10 cm से काफी अधिक) होनी चाहिए तथा परिनालिका का अनुप्रस्थ क्षेत्रफल 10^-3 m² से अधिक होना चाहिए।
माना परिनालिका की त्रिज्या r है, तब
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q15.2
अतः हम परिनालिका की त्रिज्या 2 cm से अधिक (माना 3 cm) ले सकते हैं।
अतः परिनालिका का विवरण निम्नलिखित है :
लम्बाई l = 50 cm लगभग, फेरों की संख्या N = nl = 800 x 0.5 = 400 लगभग
त्रिज्या r = 3 cm लगभग, धारा i = 10 A

प्रश्न 16.
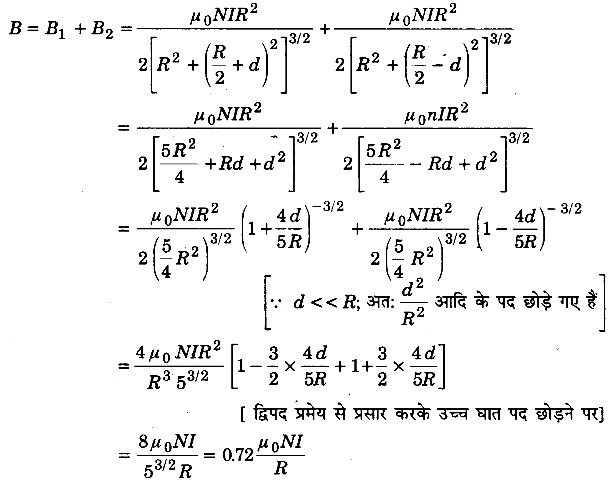
I धारावाही, N फेरों और R त्रिज्या वाली वृत्ताकार कुंडली के लिए, इसके अक्ष पर, केन्द्र से x दूरी पर स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र के लिए निम्नलिखित व्यंजक है-
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q16
(a) स्पष्ट कीजिए, इससे कुंडली के केन्द्र पर चुम्बकीय क्षेत्र के लिए सुपरिचित परिणाम कैसे प्राप्त किया जा सकता है?
(b) बराबर त्रिज्या R एवं फेरों की संख्या N, वाली दो वृत्ताकार कुंडलियाँ एक-दूसरे से R दूरी पर एक-दूसरे के समान्तर, अक्ष मिलाकर रखी गई हैं। दोनों में समान विद्युत धारा एक ही दिशा में प्रवाहित हो रही है। दर्शाइए कि कुण्डलियों के अक्ष के लगभग मध्यबिन्दु पर क्षेत्र, एक बहुत छोटी दूरी के लिए जो कि Rसे कम है, एकसमान है और इस क्षेत्र का लगभग मान निम्नलिखित है-
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q16.1
[बहुत छोटे से क्षेत्र पर एकसमान चुम्बकीय क्षेत्र उत्पन्न करने के लिए बनायी गई ऊपर वर्णित व्यवस्था हेल्महोल्ट्ज कुण्डलियों के नाम से जानी जाती है।]

प्रश्न 17.
एक टोरॉइड के (अलौह चुम्बकीय) क्रोड की आन्तरिक त्रिज्या 25 cm और बाह्य त्रिज्या 26 cm है। इसके ऊपर किसी तार के 3500 फेरे लपेटे गए हैं। यदि तार में प्रवाहित विद्युत धारा 11 A हो तो चुम्बकीय क्षेत्र को मान क्या होगा?
(i) टोरॉइड के बाहर,
(ii) टोरॉइड के क्रोड में,
(iii) टोरॉइड द्वारा घिरी हुई खाली जगह में।
हल-
दिया है, आन्तरिक त्रज्या r₁ = 0.25 m, बाह्य त्रिज्या r₂ = 0.26 m
फेरों की संख्या N = 3500, धारा i = 11 A
(i) टोरॉइड के बाहर चुम्बकीय क्षेत्र B = 0
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q17
(iii) टोरॉइड द्वारा घेरे गए रिक्त स्थान में चुम्बकीय क्षेत्र B = 0

प्रश्न 18.
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) किसी प्रकोष्ठ में एक ऐसा चुम्बकीय क्षेत्र स्थापित किया गया है जिसका परिमाण तो एक बिन्दु पर बदलता है, पर दिशा निश्चित है। (पूर्व से पश्चिम)। इस प्रकोष्ठ में एक आवेशित कण प्रवेश करता है और अविचलित एक सरल रेखा में अचर वेग से चलता रहता है। आप कण के प्रारम्भिक वेग के बारे में क्या कह सकते हैं?

(b) एक आवेशित कण, एक ऐसे शक्तिशाली असमान चुम्बकीय क्षेत्र में प्रवेश करता है। जिसको परिमाण एवं दिशा दोनों एक बिन्दु से दूसरे बिन्दु पर बदलते जाते हैं, एक जटिल पथ पर चलते हुए इसके बाहर आ जाता है। यदि यह मान लें कि चुम्बकीय क्षेत्र में इसका किसी भी दूसरे कण से कोई संघट्ट नहीं होता तो क्या इसकी अन्तिम चाल, प्रारम्भिक चाल के बराबर होगी?

(c) पश्चिम से पूर्व की ओर चलता हुआ एक इलेक्ट्रॉन एक ऐसे प्रकोष्ठ में प्रवेश करता है। जिसमें उत्तर से दक्षिण दिशा की ओर एकसमान एक विद्युत क्षेत्र है। वह दिशा बताइए जिसमें एकसमान चुम्बकीय क्षेत्र स्थापित किया जाए ताकि इलेक्ट्रॉन को अपने सरल रेखीय पथ से विचलित होने से रोका जा सके।
हल-
(a) आवेशितं कण अविचलित सरल रेखीय गति करता है, इसका यह अर्थ है कि कण पर चुम्बकीय क्षेत्र के कारण कोई बल नहीं लगा है। इससे प्रदर्शित होता है कि कण का प्रारम्भिक वेग या तो चुम्बकीय क्षेत्र की दिशा में है अथवा उसके विपरीत है।

(b) हाँ, कण की अन्तिम चाल उसकी प्रारम्भिक चाल के बराबर होगी। इसका. कारण यह है कि चुम्बकीय क्षेत्र के कारण गतिमान आवेश पर कार्यरत बल सदैव कण के वेग के लम्बवत् दिशा में लगता है जो केवल गति की दिशा को बदल सकता है परन्तु कण की चाल को नहीं।

(c) विद्युत क्षेत्र के कारण इलेक्ट्रॉन पर दक्षिण से उत्तर की ओर विद्युत बल F, कार्य करेगा, जिसके कारण इलेक्ट्रॉन उत्तर दिशा की ओर विक्षेपित होने की प्रवृत्ति रखेगा। इलेक्ट्रॉन बिना विचलित हुए सरल रेखीय गति करे इसके लिए आवश्यक है कि चुम्बकीय क्षेत्र ऐसी दिशा में लगाया जाए कि चुम्बकीय क्षेत्र के कारण इलेक्ट्रॉन पर उत्तर से दक्षिण दिशा की ओर चुम्बकीय बल कार्य करे। इसके लिए फ्लेमिंग के बाएँ हाथ के नियम से चुम्बकीय क्षेत्र ऊर्ध्वाधरत: नीचे की ओर लगाना चाहिए।

प्रश्न 19.
ऊष्मित कैथोड से उत्सर्जित और 2.0 kV के विभवान्तर पर त्वरित एक इलेक्ट्रॉन 0.15 T के एकसमान चुम्बकीय क्षेत्र में प्रवेश करता है। इलेक्ट्रॉन का गमन पथ ज्ञात कीजिए यदि चुम्बकीय क्षेत्र
(a) प्रारम्भिक वेग के लम्बवत है,
(b) प्रारम्भिक वेग की दिशा से 30° का कोण बनाता है।

प्रश्न 20.
प्रश्न 16 में वर्णित हेल्महोल्ट्ज कुंडलियों का उपयोग करके किसी लघुक्षेत्र में 0.75 T का एकसमान चुम्बकीय क्षेत्र स्थापित किया है। इसी क्षेत्र में कोई एकसमान स्थिरविद्युत क्षेत्र कुंडलियों के उभयनिष्ठ अक्ष के लम्बवत लगाया जाता है। (एक ही प्रकार के) आवेशित कणों का 15 kV विभवान्तर पर त्वरित एक संकीर्ण किरण पुंज इस क्षेत्र में दोनों कुण्डलियों के अक्ष तथा स्थिरविद्युत क्षेत्र की लम्बवत दिशा के अनुदिश प्रवेश करता है। यदि यह किरण पुंज 9.0 x 10^-5 Vm^-1, स्थिरविद्युत क्षेत्र में अविक्षेपित रहता है तो यह अनुमान लगाइए कि किरण पुंज में कौन-से कण हैं। यह स्पष्ट कीजिए कि यह उत्तर
एकमात्र उत्तर क्यों नहीं है?
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q20

प्रश्न 21.
एक सीधी, क्षैतिज चालक छड़ जिसकी लम्बाई 0.45 cm एवं द्रव्यमान 60 g है। इसके सिरों पर जुड़े दो ऊर्ध्वाधर तारों पर लटकी हुई है। तारों से होकर छड़ में 5.0 A विद्युत धारा प्रवाहित हो रही है।
(a) चालक के लम्बवत कितना चुम्बकीय क्षेत्र लगाया जाए कि तारों में तनाव शून्य हो जाए।
(b) चुम्बकीय क्षेत्र की दिशा यथावत रखते हुए यदि विद्युत धारा की दिशा उत्क्रमित कर दी जाए तो तारों में कुल आवेश कितना होगा? (तारों के द्रव्यमान की उपेक्षा कीजिए। (g = 9.8 ms^-2)
हल-
छड़ की लम्बाई l = 0.45 m व द्रव्यमान m = 0.06 kg, तार में धारा i = 5.0 A
(a) तारों में तनाव शून्य करने के लिए आवश्यक है कि चुम्बकीय क्षेत्र के कारण छड़ पर बल उसके भार के बराबर वे विपरीत हो।
अतः ilB sin 90° = mg
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q20
(b) यदि धारा की दिशा बदल दी जाए तो चुम्बकीय बल तथा छड़ का भार दोनों एक ही दिशा में हो जाएँगे।
इस स्थिति में, तारों का तनाव = mg + IlB sin 90°
= 2mg (∵ प्रथम दशा से, IlB sin 90° = mg)
= 2 x 0.06 x 9.8 = 1.176 = 1.18 N

प्रश्न 22.
एक स्वचालित वाहन की बैटरी से इसकी चालने मोटर को जोड़ने वाले तारों में 300 A विद्युत धारा (अल्प काल के लिए) प्रवाहित होती है। तारों के बीच प्रति एकांके लम्बाई पर कितना बल लगता है यदि इनकी लम्बाई 70 cm एवं बीच की दूरी 1.5 cm हो। यह बल आकर्षण बल है या प्रतिकर्षण बल ?
हल-
दिया है, तारों में धारा i₁ = i₂ = 300 A, बीच की दूरी r = 1.5 x 10^-2 m
तारों की लम्बाई = 70 cm
तारों के बीच एकांक लम्बाई पर बल
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q22
चूँकि तारों में धारा विपरीत दिशा में प्रवाहित होती है; अत: यह बल प्रतिकर्षण का होगा।

प्रश्न 23.
1.5 T का एकसमान चुम्बकीय क्षेत्र, 10.0 cm त्रिज्या के बेलनाकार क्षेत्र में विद्यमान है। इसकी दिशा अक्ष के समान्तर पूर्व से पश्चिम की ओर है। एक तार जिसमें 7.0 A विद्युत धारा प्रवाहित हो रही है। इस क्षेत्र में होकर उत्तर से दक्षिण की ओर गुजरती है। तार पर लगने वाले बल का परिमाण और दिशा क्या है, यदि
(a) तार अक्ष को काटता हो।
(b) तार N-S दिशा से घुमाकर उत्तर-पूर्व, उत्तर-पश्चिम दिशा में कर दिया जाए,
(c) N-S दिशा में रखते हुए ही तार को अक्ष से 6.0 cm नीचे उतार दिया जाए।

प्रश्न 24.
धनात्मक z-दिशा में 3000 G की एक एकसमान चुम्बकीय क्षेत्र लगाया गया है। एक आयताकार लूप जिसकी भुजाएँ 10 cm एवं 5 cm और जिसमें 12 A धारा प्रवाहित हो रही है, इस क्षेत्र में रखा है। चित्र 4.7 में दिखायी गई लूप की विभिन्न स्थितियों में इस पर लगने वाला बल-युग्म आघूर्ण क्या है? हर स्थिति में बल क्या है? स्थायी सन्तुलन वाली स्थिति कौन-सी है?

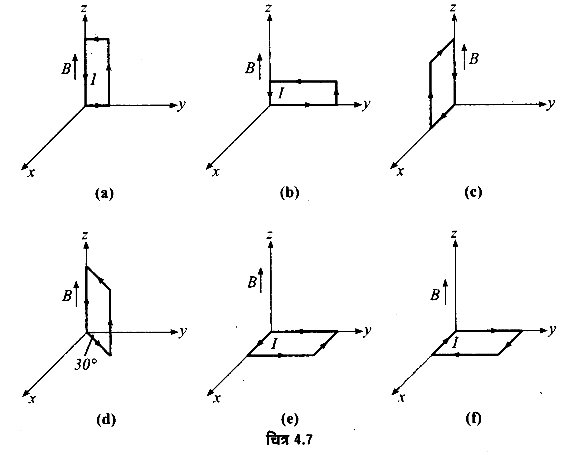
हल-
दिया है, B = 3000 G = 0.3 T, a = 0.1 m, b = 0.05 m, i = 12 A
कुंडली का क्षेत्रफल A = ab = 0.1 m x 0.05 m = 5 x 10^-3 m
(a), (b), (c), (d) प्रत्येक दशा में कुंडली के तल पर अभिलम्ब, चुम्बकीय क्षेत्र के लम्बवत् है; अतः प्रत्येक दशा में
बल-युग्म का आघूर्ण τ = iAB sin 90° = 12 x 5 x 10^-3 x 0.3 = 1.8 x 10^-2 N-m
प्रत्येक दशा में बल शून्य है, क्योंकि एकसमान चुम्बकीय क्षेत्र में रखे धारालूप पर बल-युग्म कार्य करता है परन्तु बल नहीं।
(a) τ = 1.8 x 10^-2 N-m ऋण y-अक्ष की दिशा में तथा बल शून्य है।
(b) τ = 1.8 x 10^-2 N-m ऋण y-अक्ष की दिशा में तथा बल शून्य है।
(c) τ = 1.8 x 10^-2 N-m ऋण x-अक्ष की दिशा में तथा बल शून्य है।
(d) τ = 1.8 x 10^-2 N-m तथा बल शून्य है।
(e) तथा (f) दोनों स्थितियों में कुंडली के तल पर अभिलम्ब चुम्बकीय क्षेत्र के अनुदिश है; अत:
t = iAB sin 0° = 0
अत: इन दोनों दशाओं में बल-आघूर्ण व बल दोनों शून्य हैं। यह स्थितियाँ सन्तुलन की स्थायी अवस्था में दर्शाती हैं।

प्रश्न 25.
एक वृत्ताकार कुंडली जिसमें 20 फेरे हैं और जिसकी त्रिज्या 10 cm है, एकसमान चुम्बकीय क्षेत्र में रखी है जिसका परिमाण 0.10 है और जो कुंडली के तल के लम्बवत है। यदि कुंडली में 5.0 A विद्युत धारा प्रवाहित हो रही हो तो,
(a) कुंडली पर लगने वाला कुल बल-युग्म आघूर्ण क्या है?
(b) कुंडली पर लगने वाला कुल परिणामी बल क्या है?
(c) चुम्बकीय क्षेत्र के कारण कुंडली के प्रत्येक इलेक्ट्रॉन पर लगने वाला कुलै’औसत बल क्या है?
(कुंडली 10^-5 m² अनुप्रस्थ क्षेत्र वाले ताँबे के तार से बनी है, और ताँबे में मुक्त इलेक्ट्रॉन घनत्व 10²⁹ m^-3 दिया गया है।)
हल-
फेरे N = 20, i = 5.0 A, r = 0.10 m, B = 0.10 T
इलेक्ट्रॉन घनत्व n = 10²⁹ m^-3,
तार का अनुप्रस्थ क्षेत्रफल A = 10^-5 m²
(a) कुंडली का तल चुम्बकीय क्षेत्र के लम्बवत् है; अत: कुंडली के तल पर अभिलम्ब व चुम्बकीय क्षेत्र के बीच का कोण शून्य है (θ = 0°)
बल-आघूर्ण τ = NiLAB sin 0° = 0
(b) कुंडली पर नेट बल भी शून्य है।
(c) यदि इलेक्ट्रॉनों का अपवाह वेग vd है तो
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q25

प्रश्न 26.
एक परिनालिका जो 60 cm लम्बी है, जिसकी त्रिज्या 4.0 cm है और जिसमें 300 फेरों वाली 3 परतें लपेटी गई हैं। इसके भीतर एक 2.0 cm लम्बा, 2.5 g द्रव्यमान का तार इसके (केन्द्र के निकट) अक्ष के लम्बवत रखा है। तार एवं परिनालिका का अक्ष दोनों क्षैतिज तल में हैं। तार को परिनालिका के समान्तर दो वाही संयोजकों द्वारा एक बाह्य बैटरी से जोड़ा गया है जो इसमें 6.0 A विद्युत धारा प्रदान करती है। किस मान की विद्युत धारा (परिवहन की उचित दिशा के साथ) इस परिनालिका के फेरों में प्रवाहित होने पर तारे का भार संभाल सकेगी? (g = 9.8 ms^-2)
हल-
परिनालिका की लम्बाई l = 0.6 m, त्रिज्या = 4.0 cm, फेरे N = 300 x 3
तार की लम्बाई L = 20 x 10^-2 m, द्रव्यमान m = 25 x 10^-3 kg, धारा I = 6.0 A
माना परिनालिका में प्रवाहित धारा = i
तब परिनालिका के अक्ष पर केन्द्रीय भाग में चुम्बकीय क्षेत्र

प्रश्न 27.
किसी गैल्वेनोमीटर की कुंडली का प्रतिरोध 12 Ω है। 4 mA की विद्युत धारा प्रवाहित होने पर यह पूर्णस्केल विक्षेप दर्शाता है। आप इस गैल्वेनोमीटर को 0 से 18 V परास वाले वोल्टमीटर में कैसे रूपान्तरित करेंगे ?
हल-
दिया है, G = 12 Ω, i_g = 4 mA = 4 x 10^-3 A
0 से V (V = 18 V) वोल्ट परास के वोल्टमीटर में बदलने के लिए गैल्वेनोमीटर के श्रेणीक्रम में एक उच्च प्रतिरोध R जोड़ना होगा, जहाँ
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q27.1

अत: गैल्वेनोमीटर के श्रेणीक्रम में 4488 Ω का प्रतिरोध जोड़ना होगा।

प्रश्न 28.
किसी गैल्वेनोमीटर की कुंडली का प्रतिरोध 15 Ω है। 4 mA की विद्युत धारा प्रवाहित होने पर यह पूर्णस्केल विक्षेप दर्शाता है। आप इस गैल्वेनोमीटर को 0 से 6 A परास वाले अमीटर में कैसे रूपान्तरित करेंगे?
हल-
दिया है, G = 15 Ω, i_g = 4 mA = 4.0 x 10^-3 A, i = 6 A
गैल्वेनोमीटर को 0-1 ऐम्पियर धारा परास वाले अमीटर में बदलने के लिए इसके पाश्र्वक्रम में एक सूक्ष्म प्रतिरोध S (शण्ट) जोड़ना होगा, जहाँ

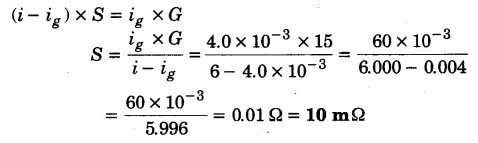
अत: इसके समान्तर क्रम में 10 mΩ का प्रतिरोध जोड़ना होगा।

परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न

प्रश्न 1.
गतिशील आवेश उत्पन्न करता है- (2013)
(i) केवल वैद्युत क्षेत्र
(ii) केवल चुम्बकीय क्षेत्र
(iii) वैद्युत एवं चुम्बकीय क्षेत्र दोनों
(iv) वैद्युत एवं चुम्बकीय क्षेत्र में से कोई नहीं
उत्तर-
(iii) वैद्युत एवं चुम्बकीय क्षेत्र दोनों

प्रश्न 2.
एक चुम्बकीय क्षेत्र उत्पन्न किया जा सकता है- (2015)
(i) केवल गतिमान आवेश द्वारा
(ii) केवल बदलते वैद्युत क्षेत्र द्वारा
(iii) (i) तथा (ii) दोनों के द्वारा
(iv) इनमें से किसी के द्वारा नहीं
उत्तर-
(iii) (i) तथा (ii) दोनों के द्वारा

प्रश्न 3.
चुम्बकीय क्षेत्र की तीव्रता का मात्रक होता है- (2011)
या
चुम्बकीय क्षेत्र का मात्रक होता है- (2015, 16)
(i) वेबर x मीटर²
(ii) वेबर/मीटर²
(iii) वेबर
(iv) वेबर/मीटर
उत्तर-
(i) वेबर/मीटर²

प्रश्न 4.
$\left( { \mu }_{ 0 }{ \varepsilon }_{ 0 } \right) ^{ \frac { -1 }{ 2 } }$ का मान है- (2011, 14, 16, 18)
(i) 3 x 10⁸ सेमी/सेकण्ड
(ii) 3 x 10¹⁰ सेमी/सेकण्ड
(iii) 3 x 10⁹ सेमी/सेकण्ड
(iv) 3 x 10⁸ किमी/सेकण्ड
उत्तर-
(ii) 3 x 10¹⁰ सेमी/सेकण्ड

प्रश्न 5.
एक इलेक्ट्रॉन तथा एक प्रोटॉन जिनकी गतिज ऊर्जाएँ समान हैं, एकसमान चुम्बकीय क्षेत्र के लम्बवत् प्रक्षेपित किए जाते हैं। पथ की त्रिज्या होगी- (2013)
(i) प्रोटॉन के लिए अधिक
(ii) इलेक्ट्रॉन के लिए अधिक
(iii) दोनों के पथ समान वक्रीय होंगे।
(iv) दोनों पथ सरल रेखीय होंगे
उत्तर-
(i) प्रोटॉन के लिए अधिक (∵ त्रिज्या ∝ द्रव्यमान)

प्रश्न 6.
एकसमान चुम्बकीय क्षेत्र B में बल रेखाओं के समान्तर एक इलेक्ट्रॉन जिसका आवेश e है, वेग v से चलता है। इलेक्ट्रॉन पर लगने वाला बल है- (2011, 14)
(i) evB
(ii) शून्य
(iii) $\frac { ev }{ B }$
(iv) $\frac { Bv }{ e }$
उत्तर-
(ii) शून्य

प्रश्न 7.
m द्रव्यमान का कण जिस पर आवेश q है एकसमान चुम्बकीय क्षेत्र B के लम्बवत् वेग v से प्रविष्ट होता है। इसके पथ की त्रिज्या होगी- (2014)
(i) $\frac { m }{ qB }$
(ii) $\frac { m }{ qvB }$
(iii) $\frac { 2m }{ qB }$
(iv) $\frac { mv }{ qB }$
उत्तर-
(iv) $\frac { mv }{ qB }$

प्रश्न 8.
एक प्रोटॉन व एक α-कण समान वेग से एकसमान चुम्बकीय क्षेत्र में लम्बवत् प्रवेश करते हैं। यदि उनके परिक्रमण काल क्रमशः T₁ व T₂ हों तब (2012)

प्रश्न 9.
किसी समान चुम्बकीय क्षेत्र में एक इलेक्ट्रॉन क्षेत्र के लम्बवत दिशा में प्रवेश करता है। इलेक्ट्रॉन का पथ होगा (2013, 15, 17)
(i) परवलयाकार
(ii) दीर्घवृत्ताकार
(iii) वृत्ताकार
(iv) सरल रैखिक
उत्तर-
(iii) वृत्ताकार

प्रश्न 10.
यदि आवेशित कण का वेग दोगुना तथा चुम्बकीय क्षेत्र का मान आधा कर दिया जाए, तो आवेश के मार्ग (पथ की त्रिज्या हो जाएगी) (2014)
(i) 8 गुनी
(ii) 4 गुनी
(iii) 3 गुनी
(iv) 2 गुनी
उत्तर-
(ii) 4 गुनी

प्रश्न 11.
एक हीलियम नाभिक 0.8 मीटर त्रिज्या के वृत्त में प्रति सेकण्ड एक चक्कर लगाता है। वृत्त के केन्द्र पर उत्पन्न चुकीय क्षेत्र होगा (2015)

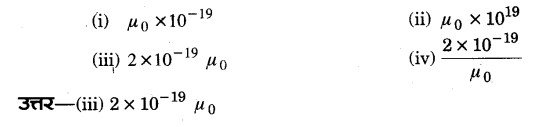
प्रश्न 12.
एक वृत्ताकार छल्ले का क्षेत्रफल 1.0 सेमी है तथा इसमें 10.0 ऐम्पियर धारा प्रवाहित हो रही है। 0.1 टेस्ला तीव्रता का चुम्बकीय क्षेत्र छल्ले के तल के लम्बवत लगाया जाता है। चुम्बकीय क्षेत्र के कारण छल्ले पर लगने वाला बल-आघूर्ण होगा (2015)
(i) शून्य
(ii) 10^-4 न्यूटन-मी
(iii) 10^-2 न्यूटन-मी
(iv) 1.0 न्यूटन-मी
उत्तर-
(iv) 1.0 न्यूटन-मी

प्रश्न 14.
एक वृत्ताकार लूप का पृष्ठ क्षेत्रफल A तथा इसमें प्रवाहित धारा I है। चुम्बकीय क्षेत्र की तीव्रता B लूप के तल के लम्बवत है। चुम्बकीय क्षेत्र के कारण लूप में लगने वाला बल आघूर्ण (2017)
(i) BIA
(ii) 2BIA
(iii) $\sigma$ BIA
(iv) शून्य
उत्तर-
(i) BIA

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
लॉरेन्ज बल क्या है? (2009, 18)
या
एक इलेक्ट्रॉन (आवेश e) + X अक्ष की दिशा में v चाल से, समरूप चुम्बकीय क्षेत्र B जो Y अक्ष की दिशा में है, प्रवेश करता है। इलेक्ट्रॉन पर कार्य करने वाले बल का सूत्र एवं दिशा ज्ञात कीजिए। (2015)
उत्तर-
चुम्बकीय क्षेत्र में गतिमान आवेश (इलेक्ट्रॉन) पर लगने वाले चुम्बकीय बल को लॉरेन्ज बल कहते हैं। यदि q आवेश v वेग से चुम्बकीय क्षेत्र $\vec { B }$ की दिशा से θ कोण पर गति करे, तो उस पर कार्य करने वाला लॉरेन्ज बल F = qvB sin θ। बल की दिशा $\vec { v }$ तथा $\vec { B }$ दोनों के लम्बवत् होती है।

प्रश्न 2.
q आवेश वाला कोई कण वेग v से एकसमान चुम्बकीय क्षेत्र B के समान्तर दिशा में गति कर रहा है। इस कण पर लगने वाले बल का मान कितना होगा? (2016)
उत्तर-
F = qvB sin θ = qvB sin 0° = 0 अर्थात् शून्य।

प्रश्न 3.
q आवेश का एक आवेशित कण, $\vec { v }$ वेग से चलता हुआ एकसमान चुम्बकीय क्षेत्र B में, क्षेत्र की दिशा से 30° का कोण बनाता हुआ प्रवेश करता है। आवेश पर लगने वाले बल का परिमाण क्या होगा? (2015)
उत्तर-
F = qvB sin θ = qvB sin 30°
F = $\frac { qvB }{ 2 }$ [∵ sin 30° = $\frac { 1 }{ 2 }$ ]

प्रश्न 4.
एक इलेक्ट्रॉन 0.1 न्यूटन/ऐम्पियर-मीटर के एकसमान चुम्बकीय क्षेत्र में लम्बवत् 10⁵ मीटर/सेकण्ड की चाल से प्रवेश करता है। इलेक्ट्रॉन पर लॉरेन्ज बल का मान ज्ञात कीजिए। (2017)
हल-
दिया है, B = 0.1 न्यूटन/ऐम्पियर-मीटर, v = 10⁵ मी/सेकण्ड
लॉरेन्ज बल (F) = qvB = 1.6 x 10^-19 x 10⁵ x 0.1 = 1.6 x 10^-15 न्यूटन

प्रश्न 5.
एक सीधे लम्बे तार से 2.0 सेमी दूरी पर चुम्बकीय क्षेत्र की तीव्रता 10^-6 टेस्ला है। तार में वैद्युत धारा ज्ञात कीजिए। (2015)

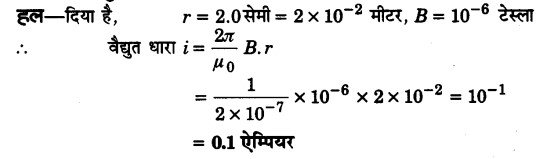
प्रश्न 6.
साइक्लोट्रॉन किस सिद्धान्त पर कार्य करता है? (2015)
उत्तर-
साइक्लोट्रॉन के कार्य करने का सिद्धान्त यह है कि डीज के बीच लगने वाले प्रत्यावर्ती विभवान्तर की रेडियो आवृत्ति, डीज के भीतर आवेशित कण के परिक्रमण की आवृत्ति के बराबर होनी चाहिए।

प्रश्न 7.
${ \mu }_{ 0 }{ \varepsilon }_{ 0 }$ का मान ज्ञात कीजिए। संकेतों के सामान्य अर्थ हैं। (2017, 18)
हल-
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism VSAQ 7

प्रश्न 8.
${ \mu }_{ 0 }{ \varepsilon }_{ 0 }$ का विमीय सूत्र लिखिए। (2017)
उत्तर-
[L^-2T²]

प्रश्न 9.
दिखाइए कि निर्वात में प्रकाश की चात $c=\frac { 1 }{ \sqrt { { \mu }_{ 0 }{ \varepsilon }_{ 0 } } }$ होती है। (2015)

प्रश्न 10.
किसी 20 सेमी त्रिज्या के वृत्ताकार लूप में 4 ऐम्पियर की धारा प्रवाहित हो रही है। लूप के केन्द्र पर चुम्बकीय क्षेत्र की गणना कीजिए। (2012, 13)
हल-
वृत्ताकार धारावाही लूप के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism VSAQ 10

प्रश्न 11.
2.0 मिमी व्यास के ताँबे के तार में 10 ऐम्पियर की धारा है। इस धारा के कारण अधिकतम चुम्बकीय क्षेत्र की तीव्रता का परिमाप ज्ञात कीजिए। (2017)

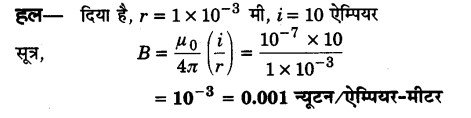
प्रश्न 12.
ऐम्पियर का परिपथीय नियम लिखिए। (2014, 15, 17, 18)
उत्तर-
“किसी बन्द वक्र के परित: चुम्बकीय क्षेत्र की तीव्रता का रेखा-समाकलन (line-integral) उस बन्द वक्र द्वारा घिरे क्षेत्रफल में से गुजरने वाली कुल वैद्युत धारा का µ0 गुना होता है, जहाँ µ0 निर्वात् की निरपेक्ष चुम्बकशीलता है।” अर्थात्

जिसमें I पथ द्वारा घिरी नेट धारा है तथा C बन्द पथ की सीमा है।

प्रश्न 13.
एक ऐम्पियर की परिभाषा दीजिए।
उत्तर-
“1 ऐम्पियर वह वैद्युत धारा है जो कि निर्वात् अथवा वायु में 1 मीटर दूर रखे दो समान्तर तारों में प्रवाहित होने पर उसकी प्रति मीटर लम्बाई पर 2 x 10^-7 न्यूटन का बल आरोपित करती है।”

प्रश्न 14.
लम्बी धारावाही परिनालिका के भीतरी अक्ष पर स्थित बिन्दु पर चुम्बकीय बल क्षेत्र का सूत्र लिखिए। (2011, 12)

प्रश्न 15.
किसी धारा लूप का क्षेत्रफल 0.25 मी² है तथा उसमें प्रवाहित धारा 0.5 ऐम्पियर है। इस लूप का चुम्बकीय आघूर्ण क्या होगा? (2017)
हल-
दिया है, A = 0.25 मीटर², I = 0.5 ऐम्पियर
चुम्बकीय आघूर्ण (M) = IA = 0.5 x 0.25 = 0.125 ऐम्पियर-मी

प्रश्न 16.
एक ऋजु रेखीय चालक में धारा से उत्पन्न चुम्बकीय बल रेखाओं की प्रकृति क्या होगी? (2009)
उत्तर-
वृत्ताकार।

प्रश्न 17.
दो समान्तर धारावाही ऋजुरेखीय तारों के बीच लगने वाले बल का सूत्र लिखिए। (2016)
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism Q19

प्रश्न 18.
किसी धारावाही अल्पांश dl से r दूरी पर चुम्बकीय क्षेत्र के लिए बायो-सेवर्ट नियम को सदिश रूप में लिखिए। (2017)
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism VSAQ 18

प्रश्न 19.
चल-कुण्डल धारामापी की सुग्राहिता से क्या तात्पर्य है? (2014)
उत्तर-
यदि किसी धारामापी में थोड़ी-सी धारा प्रवाहित करने से ही पर्याप्त विक्षेप आ जाए तो धारामापी को सुग्राही कहते हैं। कुण्डली में एकांक धारा प्रवाहित करने पर उसमें उत्पन्न विक्षेप को धारामापी की सुग्राहिता कहते हैं।

प्रश्न 20.
एक धारामापी को वोल्टमीटर में कैसे बदलते हैं? (2014)
उत्तर-
श्रेणीक्रम में उच्च प्रतिरोध जोड़ने पर धारामापी वोल्टमीटर में परिवर्तित हो जाता है।

प्रश्न 21.
किसी चल कुण्डली धारामापी का ऐमीटर और वोल्टमीटर में कैसे रूपान्तरण किया जाता (2015)
उत्तर-

धारामापी की कुण्डली के समान्तर में लघु प्रतिरोध (शन्ट) लगा देते हैं, जिसका मान ऐमीटर की परास पर निर्भर करता है। इस प्रकार चल कुण्डली धारामापी का ऐमीटर में रूपान्तरण हो जाता है।
श्रेणीक्रम में उच्च प्रतिरोध जोड़ने पर धारामापी वोल्टमीटर में परिवर्तित हो जाता है।

प्रश्न 22.
99 ओम प्रतिरोध के चल कुण्डली धारामापी में मुख्य धारा का 10% भेजने के लिए आवश्यक शन्ट के प्रतिरोध का मान ज्ञात कीजिए। (2016)

प्रश्न 23.
चुम्बकीय आघूर्ण की परिभाषा दीजिए। (2017, 18)
हल-
किसी चुम्बकीय द्विध्रुव का चुम्बकीय आघूर्ण वह बल आघूर्ण है जो इस द्विध्रुव को एकांक व एकसमान चुम्बकीय क्षेत्र में क्षेत्र की दिशा के लम्बवत् रखने पर द्विध्रुव पर लगता है।

प्रश्न 24.
चुम्बकीय बल रेखाओं एवं वैद्युत बल रेखाओं में अन्तर लिखिए। (2017)
हल-

चुम्बकीय बल रेखाएँ बन्द वक्र में होती हैं जबकि वैद्युत बल रेखाएँ बन्द वक्र में नहीं होती हैं। इसका मुख्य कारण चुम्बकीय ध्रुव का विलगित नहीं होना है जबकि धनावेश एवं ऋणावेश विलगित अवस्था में प्राप्त किए जा सकते हैं।
चुम्बकीय बल रेखाओं का किसी चुम्बकीय पदार्थ से किसी भी कोण पर निर्गमन अथवा आगमन सम्भव होता है। जबकि वैद्युत बल रेखाओं को किसी चालक पदार्थ से लम्बवत् निर्गमन अथवा आगमन होता है।

लघु उत्तरीय प्रश्न

प्रश्न 1.
m द्रव्यमान का इलेक्ट्रॉन (आवेश q), एकसमान वैद्युत क्षेत्र E में विरामावस्था से त्वरित होता है। सिद्ध कीजिए कि x-दूरी तय करने में इलेक्ट्रॉन द्वारा अर्जित वेग $\sqrt { \frac { 2qEx }{ m } }$ होगा। (2013)
उत्तर-
माना द्रव्यमान m तथा धन आवेश q का एक कण एकसमान वैद्युत क्षेत्र $\vec { E }$ में बिन्दु A पर विराम अवस्था में स्थित है (चित्र 4.8)। वैद्युत क्षेत्र द्वारा आवेशित कण पर आरोपित बल,

प्रश्न 2.
समान गतिज ऊर्जा वाले दो आवेशित कण समरूप चुम्बकीय क्षेत्र के लम्बवत प्रवेश करते हैं। यदि उनके द्रव्यमानों का अनुपात 4 : 1 तथा आवेशों का अनुपात 2 : 1 हो तो उनके वृत्तीय पथों की त्रिज्याएँ किस अनुपात में होंगी? (2014)
हल-
यहाँ दोनों कणों की गतिज ऊर्जाएँ समान हैं अर्थात् K₁ = K₂ = K तथा चुम्बकीय क्षेत्र भी समान हैं।
माना पहले कण का द्रव्यमान व आवेश क्रमशः m₁ तथा q₁ एवं द्वितीय कण का द्रव्यमान व आवेश क्रमश: m₂ तथा q₂ हैं।

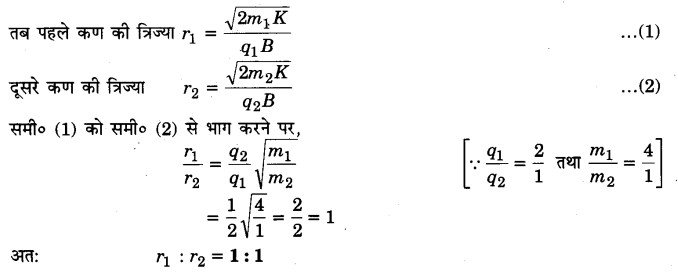
प्रश्न 3.
एक इलेक्ट्रॉन-धारा में इलेक्ट्रॉन का वेग 2.0 x 10⁷ मीटर/सेकण्ड है। इलेक्ट्रॉन 1.6 x 10³ वोल्ट/मीटर के स्थिर वैद्युत क्षेत्र के लम्बवत दिशा में 10 सेमी चलने में 3.4 मिमी विक्षेपित हो जाता है। इलेक्ट्रॉन के विशिष्ट आवेश की गणना कीजिए। (2013)
हल-
यदि कोई इलेक्ट्रॉन E तीव्रता के वैद्युत क्षेत्र में v वेग से लम्बवत् प्रवेश करके इस क्षेत्र में x दूरी तय करने पर y दूरी ऊर्ध्वाधरतः विक्षेपित हो जाए, तो

प्रश्न 4.
एक प्रोटॉन, एक ड्यूट्रॉन तथा एक α-कण समान विभवान्तर से त्वरित होकर एकसमान चुम्बकीय क्षेत्र के लम्बवत् प्रवेश करते हैं।
(i) इनकी गतिज ऊर्जाओं की तुलना कीजिए।
(ii) यदि प्रोटॉन के वृत्ताकार मार्ग की त्रिज्या 10 सेमी हो, तो ड्यूट्रॉन तथा a कण के मार्गों की त्रिज्याएँ क्या होंगी? (2017)
हल-
(i) V वोल्ट विभवान्तर से त्वरित q कूलॉम आवेश की गतिज ऊर्जा
K = qV जूल।
प्रोटॉन की गतिज ऊर्जा K_p = eV (∵ आवेश q = e)
ड्यूट्रॉन की गतिज ऊर्जा K_d = ev (∵ q = e)
α-कण की गतिज ऊर्जा Kα = 2eV (∵ q = 2e)
K_p : K_d : Kα = 1 : 1 : 2
(ii) चुम्बकीय क्षेत्र B में v चाल से गतिमान आवेशित कण (द्रव्यमान m, आवेश q) के वृत्ताकार पथ की त्रिज्या r के लिए।

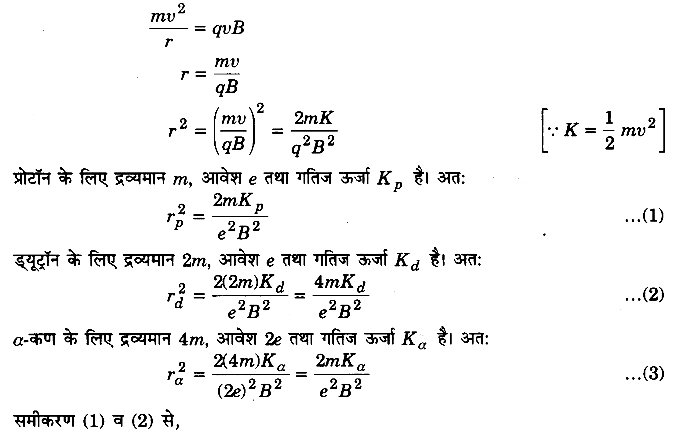
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism SAQ 4.1

प्रश्न 5.
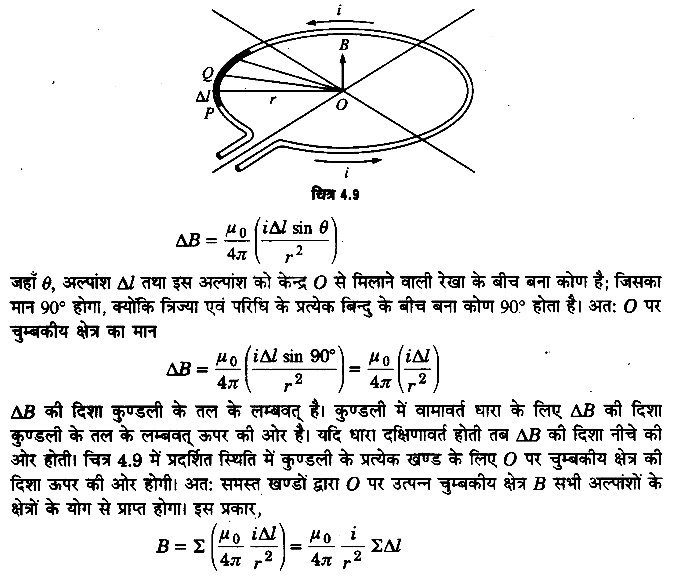
एक वृत्ताकार धारावाही कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का व्यंजक निगमित कीजिए। (2017, 18)
या
बायो-सेवर्ट का नियम समझाइए। इस नियम का उपयोग करके एक वृत्ताकार धारावाही कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र के व्यंजक का निगमन कीजिए। (2014, 16)
उत्तर-
बायो-सेवर्ट का नियम- [संकेत-दीर्घ उत्तरीय प्रश्न 2 का उत्तर पढ़िए।]
वृत्ताकार धारावाही कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र- माना एक तार को मोड़कर r मीटर त्रिज्या की वृत्ताकार कुण्डली बनाई गयी है। माना कुण्डली में i ऐम्पियर की धारा प्रवाहित हो रही है। कुण्डली के केन्द्र O पर चुम्बकीय क्षेत्र ज्ञात करने के लिए मान लेते हैं कि कुण्डली की परिधि अनेक अल्पांशों से मिलकर बनी है। इनमें से एक अल्पांश की लम्बाई ∆l है। बायो-सेवर्ट नियम के अनुसार अल्पांश ∆l के कारण O पर चुम्बकीय क्षेत्र का मान

UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism SAQ 5.1

प्रश्न 6.
0.5 एंगस्ट्रॉम त्रिज्या के वृत्त में एक इलेक्ट्रॉन 3 x 10⁵ चक्कर/सेकण्ड की दर से घूमता है। वृत्त के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र की तीव्रता ज्ञात कीजिए। (2017)
हल-
वृत्ताकार मार्ग की त्रिज्या (r) = 0.5 Å = 0.5 x 10^-10 मी
इलेक्ट्रॉन की चाल (v) = 3 x 10⁵ चक्कर/से
आवेश (q) = e = 1.6 x 10^-19 कूलॉम
इलेक्ट्रॉन की वृत्तीय पथ पर गति के कारण केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism SAQ 6

प्रश्न 7.
2 x 10^-10 मी त्रिज्या के वृत्ताकार मार्ग पर एक इलेक्ट्रॉन 3 x 10^-6 मी/से की एक समान चाल से चक्कर लगा रहा है। वृत्ताकार मार्ग के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र की गणना कीजिए।

प्रश्न 8.
किसी 10^-5 टेस्ला के एकसमान चुम्बकीय क्षेत्र में 10 eV ऊर्जा का एक इलेक्ट्रॉन वृत्ताकार मार्ग पर परिक्रमा कर रहा है। वृत्ताकार मार्ग की त्रिज्या ज्ञात कीजिए। (2017)
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism SAQ 8

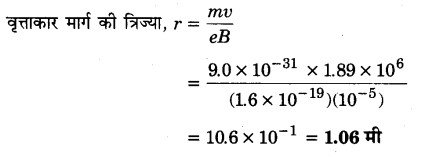
प्रश्न 9.
दो लम्बे समान्तर तारों में हैं i तथा 2i धाराएँ समान दिशा में प्रवाहित हो रही हैं। यदि तारों के बीच की लम्बवत दूरी 2a हो तब तारों के बीच मध्य बिन्दु पर चुम्बकीय क्षेत्र का मान व दिशा ज्ञात कीजिए। (2014)
हल-
ऐम्पियर की धारा के कारण बिन्दु P पर चुम्बकीय क्षेत्र

परिणामी क्षेत्र कागज के तल के लम्बवत् ऊपर की ओर होगा।

प्रश्न 10.
2.0 मीटर लम्बी परिनालिका में 1000 फेरे हैं। इसमें 10 ऐम्पियर की धारा प्रवाहित हो रही है। इसके केन्द्र में उत्पन्न चुम्बकीय क्षेत्र की तीव्रता का मान ज्ञात कीजिए। (2015)
हल-
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism SAQ 10

प्रश्न 11.
दो लम्बे सीधे तार, जिनमें प्रत्येक में 5.0 ऐम्पियर धारा प्रवाहित हो रही है, एक-दूसरे के समान्तर 2.5 सेमी की दूरी पर रखे हैं। तारों की 10.0 सेमी लम्बाई पर लगने वाला बल ज्ञात कीजिए। (2015)

प्रश्न 12.
एकसमान चुम्बकीय क्षेत्र में एक धारावाही आयताकार कुण्डली लटकायी गई है। इस पर लगने वाले बल युग्म के आघूर्ण का व्यंजक प्राप्त कीजिए। (2017)
हल-
एकसमान चुम्बकीय क्षेत्र में स्थित धारा-लूप (अथवा कुण्डली अथवा परिनालिका) को व्यवहार ठीक वैसा ही होता है जैसा दण्ड-चुम्बक का। हमने यह पढ़ा है कि चुम्बकीय क्षेत्र में स्थित धारा-लूप पर एक बल-युग्म लगता है जो कि लूप को ऐसी स्थिति में घुमाने की प्रवृत्ति रखता है जिसमें कि लूप की अक्ष चुम्बकीय क्षेत्र के समान्तर हो जाये। ठीक इसी प्रकार, चुम्बकीय क्षेत्र में लटकाया गया दण्ड-चुम्बक भी घूम कर ऐसी स्थिति में ठहरता है जिसमें कि चुम्बक की अक्ष चुम्बकीय क्षेत्र के समान्तर हो जाती है। स्पष्ट है कि चुम्बकीय क्षेत्र में स्थित दण्ड-चुम्बक पर भी एक बल-युग्म लगता है जो कि चुम्बक की अक्ष को क्षेत्र के समान्तर करने की प्रवृत्ति रखता है। चुम्बक के परमाणवीय मॉडल के अनुसार, चुम्बक का प्रत्येक परमाणु एक नन्हा धारा-लूप होता है तथा ये सभी धारा-लूप एक ही दिशा में संरेखित होते हैं चुम्बकीय क्षेत्र में इन नन्हें धारा-लूपों पर लगने वाले बल-युग्मों का योग ही चुम्बक पर लगने वाला बल-युग्म होता है (चित्र 4.12)।

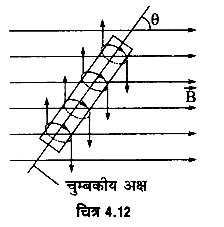
हम जानते हैं कि चुम्बकीय क्षेत्र $\vec { B }$ में, क्षेत्र की दिशा से θ कोण पर स्थित धारा-लूप पर लगने वाले बल-युग्म का आघूर्ण
= (iA) B sin θ
जहाँ A धारा-लूप को क्षेत्रफल है। यदि दण्ड-चुम्बक में N धारा-लूप हों, तब पूरे चुम्बक पर लगने वाले बल-युग्म का आघूर्ण
T = (NiA) B sin θ …..(1)
चुम्बकीय क्षेत्र में स्थित दण्ड-चुम्बक, धारा-लूप अथवा धारावाही कुण्डली का व्यवहार वैद्युत क्षेत्र में स्थित वैद्युत द्विध्रुव के व्यवहार के सदृश है। यही कारण है कि दण्ड-चुम्बक, धारा-लूप, धारावाही कुण्डली, इत्यादि ‘चुम्बकीय द्विध्रुव’ (magnetic dipole) कहलाते हैं। हम जानते हैं कि वैद्युत क्षेत्र $\vec { E }$ में क्षेत्र की दिशा से कोण पर स्थित वैद्युत द्विध्रुव पर एक बल-युग्म लगता है, जिसका आघूर्ण निम्नलिखित समीकरण के अनुसार होता है-
t = pE sin θ …..(2)
जहाँ, p वैद्युत द्विध्रुव का आघूर्ण है। समीकरण (1) व (2) की तुलना से यह स्पष्ट है कि राशि NiA, वैद्युत द्विध्रुव के आघूर्ण p के समतुल्य है। इसे चुम्बकीय द्विध्रुव आघूर्ण’ अथवा दण्ड-चुम्बक का चुम्बकीय आघूर्ण’ (magnetic moment) M कहते हैं, अर्थात्
M= NiA
चुम्बकीय आघूर्ण एक सदिश राशि है। यह चुम्बकीय अक्ष के अनुदिश दक्षिणी ध्रुव से उत्तरी ध्रुव की । ओर दिष्ट होता है।
अब, समीकरण (1) से, दण्ड-चुम्बक पर लगने वाले बल-युग्म का आघूर्ण
t = MB sin θ

प्रश्न 13.
चुम्बकीय द्विध्रुव आघूर्ण की परिभाषा दीजिए। बाह्य चुम्बकीय क्षेत्र में स्थित चुम्बकीय द्विध्रुव की स्थितिज ऊर्जा का व्यंजक प्राप्त कीजिए। (2017)
या
चुम्बकीय द्विध्रुव आघूर्ण की परिभाषा लिखिए। (2018)
उत्तर-
चुम्बकीय द्विध्रुव की ध्रुव सामर्थ्य तथा चुम्बक की प्रभावी लम्बाई के गुणनफल की चुम्बकीय द्विध्रुव आघूर्ण कहते हैं। इसे ‘M’ से प्रकट करते हैं।
जब किसी चुम्बकीय द्विध्रुव को एकसमान चुम्बकीय क्षेत्र में रखते हैं तो इस पर एक बल-युग्म का आघूर्ण कार्य करता है जो कि चुम्बकीय द्विध्रुव को बाह्य चुम्बकीय क्षेत्र की दिशा में संरेखित करने का प्रयत्न करता है। अत: चुम्बकीय द्विध्रुव को चुम्बकीय क्षेत्र की दिशा से घुमाने – में कार्य करना पड़ता है। यह कार्य ही चुम्बकीय द्विध्रुव में स्थितिज ऊर्जा के रूप में संचित हो जाता है।

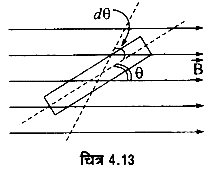
माना एक चुम्बकीय द्विध्रुव जिसका चुम्बकीय द्विध्रुव-आघूर्ण M है। एकसमान चुम्बकीय क्षेत्र B में क्षेत्र की दिशा से से कोण बनाते हुए स्थित है अत: चुम्बकीय द्विध्रुव पर कार्यरत बल-युग्म का आघूर्ण
τ = MB sin θ
चुम्बकीय द्विध्रुव को इस स्थिति से अत्यन्त सूक्ष्म कोण dθ घुमाने में किया गया कार्य
dW = tdθ = MB sin θ dθ
इसी प्रकार चुम्बकीय द्विध्रुवे को चुम्बकीय क्षेत्र में अभिविन्यास θ₁ से अभिविन्यास θ₂ तक घुमाने में किया गया कार्य

प्रश्न 14.
हाइड्रोजन परमाणु में इलेक्ट्रॉन 5.0 x 10^-11 मी त्रिज्या की कक्षा में 2 x 10⁶ मी/से की चाल से गति कर रहा है। परमाणु का चुम्बकीय आघूर्ण ज्ञात कीजिए। (2017)
या
एक परमाणु में इलेक्ट्रॉन 0.50 Å त्रिज्या की कक्षा में 4 x 10¹⁵ चक्कर/से से घूम रहा है। परमाणु के चुम्बकीय आघूर्ण का मान ज्ञात कीजिए। (2018)

प्रश्न 15.
एक धारामापी की कुण्डली का प्रतिरोध 100 ओम है। 5.0 मिली ऐम्पियर धारा से इसमें पूर्ण स्केल विक्षेपण प्राप्त होता है। इसे 0 से 10 ऐम्पियर परास के अमीटर में कैसे परिवर्तित करेंगे? (2014)

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
साइक्लोट्रॉन के सिद्धान्त एवं कार्य विधि का संक्षिप्त विवरण दीजिए। साइक्लोट्रॉन की सीमाओं का उल्लेख कीजिए। (2017)
हल-
सिद्धान्त- चुम्बकीय क्षेत्र में परिक्रमण करने वाले आवेशित कणों की परिक्रमण आवृत्ति कण की ऊर्जा पर निर्भर नहीं करती है। अत: क्रॉसित (परस्पर लम्बवत्) वैद्युत तथा चुम्बकीय क्षेत्रों का उपयोग कर आवेशित कण को चुम्बकीय क्षेत्र की सहायता से बार-बार एक ही वैद्युत क्षेत्र से गुजारकर उसको उच्च ऊर्जा तक त्वरित किया जा सकता है।

कार्य-विधि- माना m द्रव्यमान तथा +q आवेश का एक आयन, आयन-स्रोत से उस क्षण निर्गत होता है जबकि D₂ ऋण विभव पर है। यह आयनन डीज के बीच के अन्तराल में विद्यमान वैद्युत क्षेत्र के द्वारा D₂ की ओर को त्वरित होकर D₂ में वेग v (माना) से प्रवेश कर जाता है। डीज के भीतर प्रवेश करते ही यह आयन डीज की धात्विक दीवारों द्वारा वैद्युत क्षेत्र से परिरक्षित कर दिया जाता है। अब डीज के तल के लम्बवत् चुम्बकीय क्षेत्र के कारण आयन नियत चाल v से त्रिज्या r के वृत्ताकार पथ पर चलने लगता है। आयन की वृत्तीय गति के लिए आवश्यक अभिकेन्द्र बल, उस पर कार्यरत चुम्बकीय बल से प्राप्त होता है। अतः अभिकेन्द्र बल = चुम्बकीय बल।
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism LAQ 1

साइक्लोट्रॉन की सीमाएँ-
(i) साइक्लोट्रॉन द्वारा अनावेशित कण जैसे- न्यूट्रॉन (जो कि नाभिकीय क्रियाओं के लिए सर्वश्रेष्ठ प्रक्षेप्य कण है) को त्वरित नहीं किया जा सकता है।
(ii) साइक्लोट्रॉन द्वारा इलेक्ट्रॉनों को त्वरित नहीं किया जा सकता है क्योंकि इनका द्रव्यमान बहुत कम होता है, अतः सूक्ष्म गतिज ऊर्जा ग्रहण कर ही ये बहुत उच्च वेग से गति करने लगते हैं।
(iii) साइक्लोट्रॉन द्वारा आवेशित कणों को इतने उच्च वेग तक त्वरित नहीं किया जा सकता है कि उनका वेग प्रकाश के वेग के तुल्य हो जाए क्योंकि इतने उच्च वेग पर आवेशित कणों का द्रव्यमान नियत न रहकर वेग के साथ परिवर्तित होता हैं। यदि आवेशित कण का विराम द्रव्यमान m₀ हो तथा v वेग से गति करते समय कण का वेग m हो, तब
$m=\frac { { m }_{ 0 } }{ \sqrt { 1-\frac { { v }^{ 2 } }{ { c }^{ 2 } } } }$
जहाँ, c निर्वात् में प्रकाश की चाल है।

प्रश्न 2.
धारावाही चालक के कारण उत्पन्न चुम्बकीय क्षेत्र की तीव्रता से सम्बन्धित बायो-सेवर्ट नियम की व्याख्या कीजिए। बायो-सेवर्ट नियम की समीकरण से निर्वात की चुम्बकशीलता का मात्रक एवं विमीय समीकरण निकालिए। (2017)
या
बायो-सेवर्ट नियम को शब्दों तथा सूत्र में लिखिए। (2011)
या
बायो-सेवर्ट नियम का उल्लेख कीजिए। (2013, 17, 18)
या
किसी धारावाही चालक के कारण उत्पन्न चुम्बकीय क्षेत्र के सम्बन्ध में बायो-सेवर्ट के नियम का उल्लेख कीजिए। (2015)
उत्तर-
बायो-सेवर्ट का नियम (Biot-Savart Law)- सन् 1820 में बायो तथा सेवर्ट ने धारावाही चालकों द्वारा उत्पन्न चुम्बकीय क्षेत्र का अध्ययन करने के लिए अनेक प्रयोग किये। इन प्रयोगों के आधार पर उन्होंने बताया कि किसी धारावाही चालक के एक अल्पांश ∆l के द्वारा उत्पन्न चुम्बकीय क्षेत्र में किसी बिन्दु P पर क्षेत्र का मान ∆B निम्नलिखित बातों पर निर्भर करता है-

UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism LAQ 2.1

प्रश्न 3.
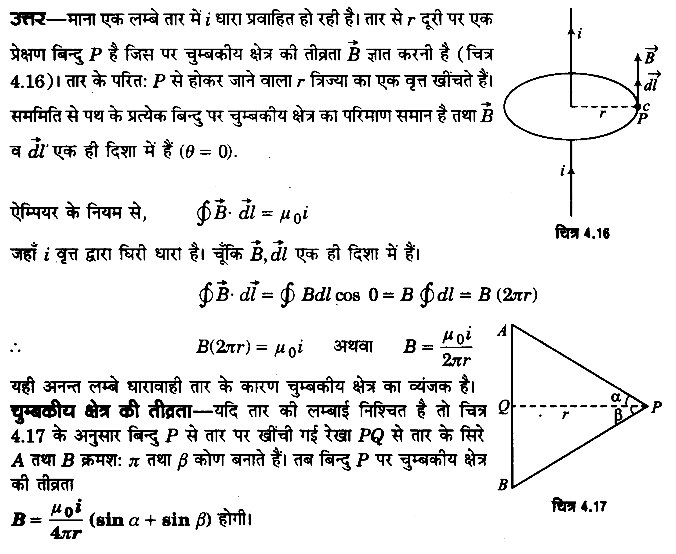
ऐम्पियर के परिपथीय नियम का उपयोग करके एक अनन्त लम्बाई के सीधे धारावाही चालक के कारण उत्पन्न चुम्बकीय क्षेत्र का सूत्र स्थापित कीजिए। (2014)
या
ऐम्पियर के परिपथीय नियम का उपयोग करके अनन्त लम्बाई के सीधे धारावाही तार के निकट किसी बिन्दु पर चुम्बकीय क्षेत्र की तीव्रता ज्ञात कीजिए। (2015)

प्रश्न 4.
ऐम्पियर के परिपथीय नियम की सहायता से धारावाही परिनालिका के अन्दर उसकी अक्ष पर चुम्बकीय क्षेत्र के सूत्र की स्थापना कीजिए। (2015)
उत्तर-
माना एक लम्बी परिनालिका की प्रति मीटर लम्बाई में तार के n फेरे हैं तथा इसमें i ऐम्पियर की धारा बह रही है। माना एक आयताकार बन्द पथ a b c d है जिसकी भुजा a b परिनालिका की अक्ष के समान्तर है तथा भुजाएँ। c तथा a d बहुत लम्बी हैं जिससे कि यह माना जा सके कि भुजा c d परिनालिका से बहुत दूर है तथा इस भुजा पर परिनालिका के कारण चुम्बकीय क्षेत्र नगण्य है। जब परिनालिका लम्बी है। तथा आयताकार बन्द पथ परिनालिका के किसी भी किनारे के बहुत समीप नहीं है, तो क्षेत्र b c तथा a d भुजाओं के लम्बवत् हैं।
UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism LAQ 4

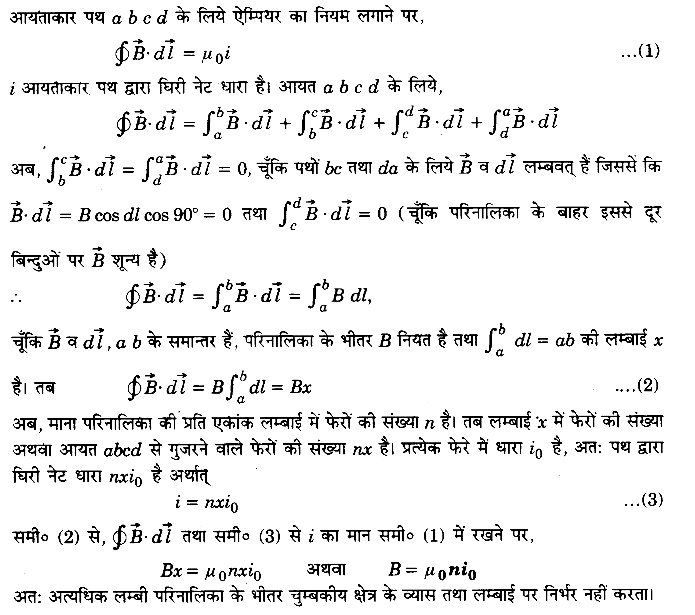
प्रश्न 5.
दो समान्तर धारावाही चालकों के बीच लगने वाले बल $\frac { F }{ l } =\frac { { \mu }_{ 0 } }{ 2\Pi } =\frac { { i }_{ 1 }{ i }_{ 2 } }{ r }$ न्यूटन/मीटर के लिए सूत्र व्युत्पन्न कीजिए। उपर्युक्त सूत्र के आधार पर धारा के एक ऐम्पियर की परिभाषा दीजिए। (2017)
या
दो समान्तर धारावाही चालकों के बीच क़ार्य करने वाले बल का सूत्र ज्ञात कीजिए। (2012, 17, 18)
या
दो समान्तर धारावाही चालकों के बीच लगने वाले बल के लिए सूत्र स्थापित कीजिए। इसके आधार पर वैद्युत धारा के मात्रक ऐम्पियर की परिभाषा दीजिए। (2013)
या
L मीटर लम्बाई के दो समान्तर तारों, जिनके मध्य की दूरी r मीटर है तथा जिनमें i1 और i2 ऐम्पियर की विद्युत धाराएँ प्रवाहित हैं, के मध्य प्रति एकांक लम्बाई पर बल का सूत्र $\frac { F }{ L } =\frac { { \mu }_{ 0 } }{ 2\Pi } =\frac { { i }_{ 1 }{ i }_{ 2 } }{ r }$ व्युत्पादित कीजिए। इस सूत्र से ऐम्पियर की परिभाषा दीजिए। (2015)
उत्तर-
धारावाही चालक के चारों ओर एक चुम्बकीय क्षेत्र उत्पन्न हो जाता है तथा चुम्बकीय क्षेत्र में स्थित धारावाही चालक पर एक बल कार्य करता है। अत: यदि एक धारावाही चालक के निकट कोई दूसरा धारावाही चालक रखा जाये तो यह चालक पहले चालक द्वारा उत्पन्न चुम्बकीय क्षेत्र के कारण एक बल का अनुभव करेगा। इसी प्रकार पहला धारावाही चालक दूसरे धारावाही चालक द्वारा उत्पन्न चुम्बकीय क्षेत्र के कारण एक बल अनुभव करेगा। स्पष्ट है कि पास-पास रखे दो धारावाही चालक चुम्बकीय क्षेत्र की पारस्परिक क्रिया के कारण एक-दूसरे पर बल लगाते हैं।

पारस्परिक बल का परिमाण एवं प्रकृति- माना दो लम्बे ऋजुरेखीय तार P९ तथा RS वायु या निर्वात् में एक-दूसरे के समीप परस्पर समान्तर रखे हैं। इनके बीच की दूरी r है (चित्र 4.20)। माना PQ एवं RS में प्रवाहित धाराएँ क्रमशः i₁ एवं i₂ हैं। PQ में प्रवाहित धारा । के कारण चालक RS के किसी भी बिन्दु पर चुम्बकीय क्षेत्र

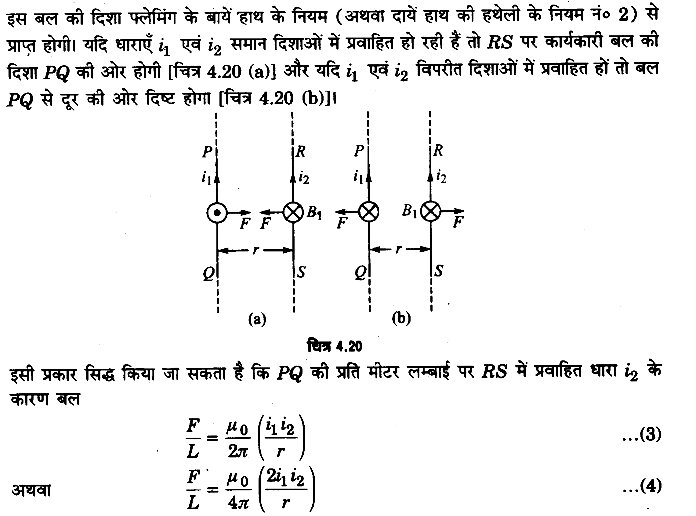
इसकी दिशा भी फ्लेमिंग के बायें हाथ के नियम अथवा दायें हाथ की हथेली के नियम नं० 2 से निर्धारित की जाएगी। यदि धारा i₂ उसी दिशा में है जिसमें i₁ है तो PQ पर लगने वाला बल चालक RS की ओर दिष्ट होगा। [चित्र 4.20 (a)] और यदि यह विपरीत दिशा में है तो यह RS से दूर दिष्ट होगा [चित्र 4.20 (b)]। अतः उपर्युक्त विवेचना से यह स्पष्ट होता है कि यदि दो समान्तर तारों में धाराएँ एक ही दिशा में हैं तो वे एक-दूसरे को आकर्षित करते हैं और यदि धाराएँ विपरीत दिशा में हैं तो तार एक-दूसरे को प्रतिकर्षित करते हैं।

प्रश्न 6.
आवश्यक सिद्धान्त देते हुए चल कुण्डली गैल्वेनोमीटर की संरचना तथा कार्यविधि का वर्णन कीजिए। (2014)
या
चल कुण्डली धारामापी का सिद्धान्त एवं कार्यविधि का वर्णन कीजिए। इसकी सुग्राहिता किस प्रकार बढ़ायी जा सकती है? (2017)
या
निम्नलिखित चल कुण्डली धारामापी का सिद्धान्त लिखिए एवं उसकी धारा सुग्राहिता का व्यंजक ज्ञात कीजिए। (2018)
उत्तर-
चल कुण्डली गैल्वेनोमीटर- ये निम्न दो प्रकार के होते हैं
1. निलम्बित कुण्डली धारामापी- यह वैद्युत-धारा के संसूचन (detection) तथा मापन (measurement) के लिए प्रयुक्त किया जाने वाला उपकरण है। इसकी क्रिया चुम्बकीय क्षेत्र में धारावाही कुण्डली पर कार्यरत् बलाघूर्ण पर आधारित है।
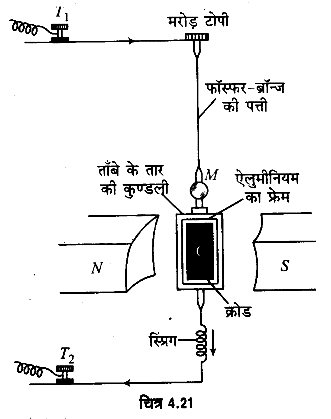
संरचना- इसमें एक आयताकोर कुण्डली होती है जोकि ताँबे के पतले पृथक्कृत (insulated) तार के ऐलुमीनियम के फ्रेम के ऊपर लपेटकर बनायी जाती है (चित्र 4.21)।

इस कुण्डली को एक पतली फॉस्फर-ब्रॉन्ज मरोड़ टोपी (phosphor-bronze) की पत्ती (strip) से एक स्थायी घोड़ा-नाल चुम्बक (horse-shoe magnet) NS के बेलनाकार ध्रुव-खण्डों फॉस्फर-ब्रॉन्ज (pole-pieces) के बीच लटकाया जाता है। पत्ती को ऊपरी सिरा एक मरोड़ टोपी (torsion head) से जुड़ा होता है। कुण्डली का निचला सिरा एक अत्यन्त पतले की कुण्डली का फ्रेम फॉस्फर-ब्रॉन्ज के तार के ढीले-वेष्ठित स्प्रिंग (loosely-wound spring) से जुड़ा होता है। कुण्डली के भीतर एक नर्म लोहे की क्रोड C सममित तथा बिना कुण्डली को स्पर्श किए रखी जाती है। क्रोड बल-रेखाओं को संकेन्द्रित कर देती है तथा इस प्रकार ध्रुव-खण्डों के स्प्रिंग छ। बीच चुम्बकीय क्षेत्र ‘प्रबल हो जाता है। निलम्बन पत्ती (suspension strip) के। निचले भाग पर एक छोटा दर्पण (mirror) M लगा होता है, जो पत्ती के साथ-साथ घूमती है तथा जिसका विक्षेप एक लैम्प तथा पैमाने (lamp and scale arrangement) की सहायता से पढ़ा जा सकता है। सम्पूर्ण प्रबन्ध को एक धात्विक बक्से में बन्द रखा जाता है (चित्र 4.21 में प्रदर्शित नहीं) जिसके सामने की ओर काँच की एक खिड़की तथा आधार पर समतलकारी पेंच (levelling screws) लगे होते हैं।

धारा जिसको मापने करना हो, एक टर्मिनल (terminal) T₁ से प्रवेश करती है तथा निलम्बन, कुण्डली व स्प्रिंग से होकर दूसरे टर्मिनल T₂ से निर्गत होती है। स्थायी चुम्बक के ध्रुव खण्ड बेलनाकार रखे जाते हैं ताकि कुण्डली की प्रत्येक स्थिति में चुम्बकीय क्षेत्र त्रिज्य (radial) रहे अर्थात् कुण्डली का तल प्रत्येक स्थिति में बल-रेखाओं के समान्तर रहे।
सिद्धान्त- जब कुण्डली में धारा 1 प्रवाहित की जाती है तो कुण्डली पर लगने वाला बल-आघूर्ण
T= N i AB sin 90° = NiBA

यहाँ θ कुण्डली के तल पर लम्ब की दिशा तथा चुम्बकीय क्षेत्र $\vec { B }$ की दिशा के बीच कोण है। A कुण्डली का क्षेत्रफल तथा N कुण्डली में फेरों की संख्या है।
धारामापी में चुम्बकीय क्षेत्र $\vec { B }$ को, ध्रुवखण्डों N व S को बेलनाकार बनाकर तृथा कुण्डली के भीतर नर्म लोहे की बेलनाकार क्रोड रखकर “त्रिज्य’ (radial) बनाया जाता है। इस दिशा में कुण्डली के तल पर अभिलम्ब चुम्बकीय क्षेत्र B से सदैव समकोण पर होगा (चित्र 4.21) अर्थात् θ = 90° होगा। अत: कुण्डली पर कार्यरत् बलाघूर्ण
t = Ni B A sinθ [θ= 90°]
= NiB A

यदि निलम्बन पत्ती की मरोड़ दृढ़ता (torsional rigidity) c हो तथा निलम्बन पत्ती में ऐंठन Φ हो, तो प्रत्यानयन बल-युग्म = cΦ होगा।
साम्यावस्था के लिये,
विक्षेपक बल-युग्म आघूर्ण = प्रत्यानयन बल-युग्म का आघूर्ण
N i A B = cΦ
i = $\frac { c }{ NAB }$ Φ = kΦ
जहाँ, k = c/NAB उपकरण का नियतांक है। जिसे धारा परिवर्तन गुणांक (current reduction factor) भी कहते हैं। अतः धारामापी में प्रवाहित धारा, उत्पन्न विक्षेप के अनुक्रमानुपाती होती है।

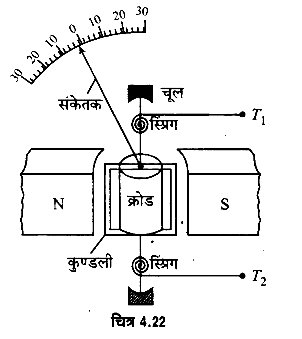
2. कीलकित-कुण्डली अथवा वेस्टन धारामापी- यह भी चल कुण्डली धारामापी है। यह निलम्बित-कुण्डली धारामापी की अपेक्षा कुछ कम सुग्राही होता है परन्तु अधिक सुविधाजनक है। इसमें ताँबे के महीन पृथक्कृत तार की, ऐलुमीनियम के फ्रेम पर लिपटी कुण्डली एक स्थायी तथा शक्तिशाली नाल-चुम्बक के ध्रुव-खण्डों के बीच दो चूलों (pivots) पर झूलती है (चित्र 4.22)। कुण्डलियों के दोनों सिरों पर चूलों के पास दो क्रोड स्प्रिंग लगे रहते हैं जो कुण्डली के घूमने पर ऐंठन बल-युग्म उत्पन्न करते हैं तथा कुण्डली को दो कुण्डली स्प्रिंग : सम्बन्धक-पेचों T₁ व T₂ से जोड़ते हैं। कुण्डली का विक्षेप पढ़ने के लिए कुण्डली के साथ एक ऐलुमीनियम का लम्बा संकेतक लगा रहता है जो एक वृत्ताकार पैमाने पर घूमता है। पैमाने पर बराबर दूरियों पर चिह्न लगे रहते हैं तथा शून्यांक चिह्न बीच में होता है। अतः धारामापी के सम्बन्धक-पेचों पर धन व ऋण के चिह्न नहीं बने होते। चुम्बकीय क्षेत्र को त्रिज्य बनाने के लिए इससे भी ध्रुव-खण्ड अवतलाकार कटे होते हैं तथा कुण्डली के अन्दर मुलायम लोहे की क्रोड लगी होती है। इसका सिद्धान्त के कार्यविधि चल-कुण्डली धारामापी के समान ही है। इसकी सहायता से 10^-6 ऐम्पियर तक की वैद्युत धारा नापी जा सकती है। धारामापी की सुग्राहिता N, A तथा B का मान बढ़ाकर तथा c का मान कम करके बढ़ाई जा सकती है।

प्रश्न 7.
किसी धारामापी को अमीटर में कैसे परिवर्तित करेंगे? उपयुक्त परिपथ द्वारा स्पष्ट कीजिए। (2014, 18)
उत्तर-
धारामापी का अमीटर में रूपान्तरण- अमीटर वह यन्त्र है जो वैद्युत परिपथ में धारा की प्रबलता सीधे ऐम्पियर में नापने के काम आता है। मिलीऐम्पियर की कोटि की धारा नापने वाले यन्त्र को मिलीअमीटर कहते हैं।

अमीटर मूलतः धारामापी ही होता है जिसे परिपथ के श्रेणीक्रम में डाल देते हैं ताकि नापी जाने वाली सम्पूर्ण धारा इसमें से होकर जाये। तब अमीटर में उत्पन्न विक्षेप अमीटर से होकर जाने वाली धारा की माप देगा (Φ ∝ i)। परन्तु चूँकि अमीटर की अपनी कुण्डली का भी कुछ प्रतिरोध होता है अतः इसे परिपथ के श्रेणीक्रम में जोड़ने पर परिपथ का प्रतिरोध बढ़ जायेगा जिससे परिपथ में धारा घट जायेगी। अतः अमीटर द्वारा पढ़ा गया धारा का मान, उस धारा के मान से कम होगा जिसे नापना था। अत: यह आवश्यक है कि अमीटर का अपना प्रतिरोध, जितना हो सके कम होना चाहिए ताकि इसे परिपथ में डालने पर नापी जाने वाली धारा का मान न बदले।

स्पष्ट है इस त्रुटि को पूर्णतः दूर करने के लिए RA का मान शून्य होना चाहिए अर्थात् एक आदर्श अमीटर का अपना प्रतिरोध शून्य होना चाहिए परन्तु शून्य प्रतिरोध का अमीटर प्राप्त नहीं किया जा सकता। अतः व्यवहार में, एक अच्छे अमीटर का अपनी प्रतिरोध परिपथ में उपस्थित अन्य प्रतिरोधों की तुलना में बहुत कम होना चाहिए अर्थात्
R_A << R₁ + R₂
तब i का मान लगभग i के ही बराबर होगा।

साधारणतः कीलकित (pivoted type) चल-कुण्डली धारामापी को। ही अमीटर के रूप में प्रयुक्त किया जाता है। इसके लिए इसकी कुण्डली के समान्तर क्रम में एक छोटा प्रतिरोध डाल देते हैं जिसे ‘शन्ट’ (shunt) कहते हैं (चित्र 4.24)। इस प्रबन्ध का संयुक्त प्रतिरोध धारामापी की कुण्डली तथा शन्ट दोनों के अलग-अलग प्रतिरोधों से कम होता है। अतः जब इसे किसी परिपथ में डालते हैं तो अमीटर यह परिपथ की धारा में कोई विशेष परिवर्तन नहीं करता। इस प्रकार । चित्र 4.24 यह प्रबन्ध एक अच्छे अमीटर का कार्य करता है।

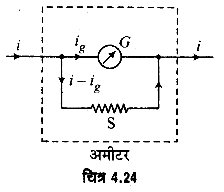
धारामापी में शन्ट लगाने का एक अन्य लाभ भी है। यदि शन्ट न हो तब परिपथ की पूरी धारा कुण्डली में से होकर जायेगी। इस दशा में धारामापी द्वारा अधिक-से-अधिक उतनी धारा नापी जा सकती है जिससे कि कुण्डली में पूरे पैमाने का विक्षेप (full-scale deflection) हो जाये। शन्ट के होने पर, परिपथ की धारा का केवल एक छोटा भाग ही कुण्डली से होकर जाता है, अधिकांश भाग शन्ट से होकर निकल जाता है। चूंकि कुण्डली का विक्षेप कुण्डली में को जाने वाली धारा के अनुक्रमानुपाती होता है, अत: कुण्डली का विक्षेप काफी कम हो जाता है। अतः अब परिपथ में पहले से कहीं अधिक धारा होने पर कुण्डली में पूरे पैमाने का विक्षेप होता है। इस प्रकार, शन्टयुक्त धारामापी (अमीटर) कहीं अधिक मान की धारा को नाप सकता है। दूसरे शब्दों में, शन्ट लगाने से मापन की परास (range) बढ़ जाती है। (यद्यपि सुग्राहिता घट जाती है)। वास्तव में शन्ट के प्रतिरोध का मान इसी से निर्धारित किया जाता है कि अमीटर किस परास को बनाना है।

माना कि परिपथ की धारा i है, धारामापी की कुण्डली का प्रतिरोध G तथा शन्ट का प्रतिरोध S है। माना। कि धारा का i_g भाग कुण्डली G में तथा शेष भाग (i – i_g) शन्ट S में होकर जाता है। चूंकि G व S समान्तर, में हैं, अतः उनके सिरों के बीच एक ही विभवान्तर होगा।

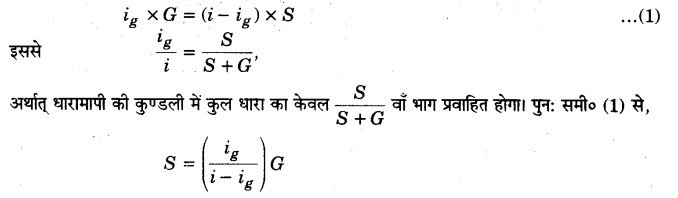
यदि कुण्डली में धारा ig, के द्वारा पूरे पैमाने का विक्षेप हो तो परिपथ में धारा i होने पर पूरे पैमाने का विक्षेप होगा। अतः स्पष्ट है कि धारामापी के समान्तर में उपरोक्त मान का शन्ट लगाने पर धारामापी, ऐम्पियर की परास का अमीटर होगा। एक दिये गये धारामापी के लिए i_g का मान प्रयोग द्वारा ज्ञात किया जा सकता है।

We hope the UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism (गतिमान आवेश और चुम्बकत्व) help you.

UP Board Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism (गतिमान आवेश और चुम्बकत्व)

Leave a Reply Cancel reply