UP Board Solutions for Class 7 Maths Chapter 4 रचनाएँ

अभ्यास 4 (a)

प्रश्न 1.
6 सेमी माप के एक रेखाखण्ड को दो बराबर भागों में परकार और पटरी की सहायता से विभाजित कीजिए।

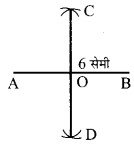
हल :
ज्ञात है – रेखाखण्ड AB।
रचना करनी है – रेखाखण्ड AB का समद्विभाजन।
रचना –

सर्वप्रथम रेखाखण्ड AB = 6.0 सेमी खींचा।
रेखाखण्ड AB = $\frac { 6.0 }{ 2 }$ =3.0 सेमी से अधिक त्रिज्या लेकर रेखाखण्ड के अन्त्य बिन्दु को A को केन्द्र मानकर परकार की सहायता से AB के दोनों ओर चाप खींचें।
रेखाखण्ड AB के दूसरे अन्त्य बिन्दु B को केन्द्र मानकर उसी त्रिज्या से AB के दोनों ओर चाप खींचें जो पहले चाप को बिन्दुओं C और D पर काटता है।
CD को मिलाया जो रेखाखण्ड AB को 0 बिन्दु पर समद्विभाजित करता है।

प्रश्न 2.
3 सेमी त्रिज्या का एक वृत्त जिसका केन्द्र 0 है, अपनी अभ्यास पुस्तिका – 3 पर खींचिए। इसमें दो जीवाएँ PQ और RS लीजिए। इन दोनों रेखाखण्डों के लम्ब समद्विभाजक खींचिए। ये दोनों लम्ब समद्विभाजक किस बिन्दु पर मिलते हैं?

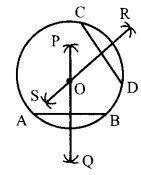
रचना – सर्वप्रथम- को केन्द्र मानकर 3 सेमी त्रिज्या का वृत्त खींचा। इस 17B वृत्त पर दो जीवाएँ AB और CD खींची। जीवा AB और CD के लम्ब समद्विभाजक किए। ये दोनों लम्बे समद्विभाजक वृत्त के केन्द्र 0 पर मिलते हैं।

प्रश्न 3.
8 सेमी माप के रेखाखण्ड को चार बराबर भागों में बाँटिए।
हल :
ज्ञात है – रेखाखण्ड AB= 8 सेमी।।
रचना करनी है – रेखाखण्ड AB को चार बराबर भागों में विभाजित करना।
रचना –

सर्वप्रथम रेखाखण्ड AB = 8 सेमी खींचा।
रेखाखण्ड AB = $\frac { 8 }{ 2 }$ = 4 सेमी से अधिक त्रिज्या लेकर बिन्दु A को केन्द्र मानकर रेखाखण्ड AB के दोनों ओर चाप लगायें।
उसी त्रिज्या को लेकर बिन्दु B को केन्द्र मानकरे रेखाखण्ड AB की दोनों ओर चाप लगाते हैं जो एक दूसरे की M और N पर काटते हैं MN रेखाखण्ड AB को बिन्दु C पर काटता है।
AC = BC
इसी प्रकार AC तथा BC को भी बराबर-बराबर भागों में विभाजित करते हैं। रेखाखण्ड AC को QR रेखाखण्ड BC को बिन्दु E पर काटता है।
इस प्रकार AB चार बराबर भागों में विभाजित हो जाती है।

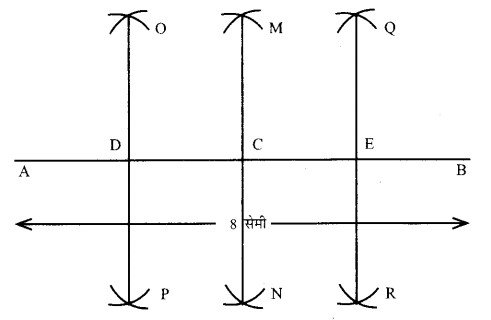
प्रश्न 4.
परकार की सहायता से 4 सेमी त्रिज्या का एक वृत्त खींचिए। वृत्त पर एक जीवा खींचिए। वृत्पर पर एक जीवा खींचिए। वृत्त के केन्द्र से जीवा के मध्य बिन्दु की दूरी माप कर ज्ञात कीजिए।

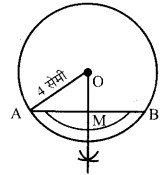
हल :
ज्ञात है – 4 सेमी त्रिजया का एक वृत्त।
ज्ञात करना है – वृत्त के केन्द्र से जीवा के मध्य बिन्दु की दूरी की माप।
रचना –

सर्वप्रथम 4 सेमी त्रिज्या का एक वृत्त खींचा।
वृत्त के केन्द्र 0 से कुछ दूरी पर कोई भी जीवा AB खींचा।
अब वृत्त के केन्द्र 0 से जीवा AB पर लम्ब OM खींचा जो जीवा AB के मध्यबिन्दु पर मिलता है।
OM = 2.4 सेमी

प्रश्न 5.
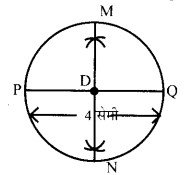
4 सेमी का एक रेखाखण्ड P Q खींचिए। इसके लम्बावर्द्धक कीजिए जो रेखा P Q को बिन्दु D पर काटे, क्या PD = Q D है? पुनः PD त्रिज्या का एक वृत्त खींचिए और देखिए क्या यह वृत्त बिन्दु P और Q से होकर हा रहा है।

हल :
ज्ञात है – रेखाखण्ड P Q=4 सेमी रचना करनी है PD=Q D
रचना –

सर्वप्रथम रेखाखण्ड P Q=4 सेमी खींचा। 4 सम्मे
बिन्दु P को केन्द्र मानकर P Q के आधे से अधिक की त्रिज्या लेकर P Q के दोनों ओर चाप लगायें।
उसी त्रिज्या को लेकर बिन्दु Q से P Q के दोनों ओर फिर से चाप लगाया जो M और N पर काटते हैं।
MN को मिलाने पर यह रेखाखण्ड P Q को बिन्दु D पर काटते हैं।
PD=D Q
D को केन्द्र मानकर PD त्रिज्या लेकर एक वृत्त खींचा जो P Q से होकर जाता है।

प्रश्न 6.
6.4 सेमी का एक रेखाखण्ड AB खींचिए और उसका सममित अक्ष खीचिए।
नोट – विद्यार्थी स्वयं करें।

अभ्यास 4 (b)

प्रश्न 1.
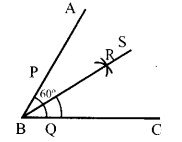
अपनी अभ्यास पुस्तिका पर एक 60° का कोण बनाकर पटरी परकार की सहायता से उसे समद्विभाजित कीजिए।

हल :
ज्ञात है – 60° का कोण। रचना करनी है – 60° के कोण का समद्विभाजन।
रचना – सर्वप्रथम 60° का एक कोण बनाया। शीर्ष B को केन्द्र मानकर किसी भी त्रिज्या से एक चाप खींचा जो भुजा BA तथा BC को क्रमशः P और Q बिन्दुओं पर काटता है। P और Q को केन्द्र मानकर उसी त्रिज्या से चाप लगाए जो एक-दूसर को R पर काटते हैं। BR को मिलाकर S तक आगे बढ़ाया। रेखाखण्ड BS, ∠ABC = 60° को समद्वि भाजित करता है।

प्रश्न 2.
कोई कोण PQR खींचिए। एक किरण QS इस प्रकार खींचिए कि ∠PQS = ∠RQS।
UP Board Solutions for Class 7 Maths Chapter 4 रचनाएँ 7
रचना – सर्वप्रथम किसी भी माप का एक कोण PQR बनाया, फिर , A प्रश्न 1 की भाँति ∠ PQR की समद्विभाजक किरण QS खींची।
मापने पर, ∠PQS = ∠ RQs

प्रश्न 3.
एक 120° का कोण खींचकर पटरी परकार की सहायता से इसको चार बराबर भागों में विभक्त कीजिए और नापकर सत्यापित कीजिए।

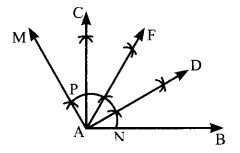
रचना – सर्वप्रथम पटरी व परकार की सहायता से 120° का कोण CAB बनाया। 120° के कोण का समद्विभाजन करने पर कोण M DAB तथा CAD प्राप्त हुआ। कोण DAB व कोण CAD को भी समद्विभाजित किया। अतः 120° का कोण CAB चार बराबर भागों में विभाजित हो गया।

प्रश्न 4.
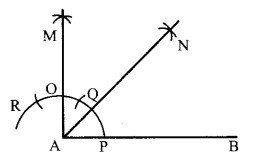
एक समकोण बनाइए तथा उसके समद्विभाजक की रचना कीजिए।

उत्तर :
रचना – सर्वप्रथम एक रेखाखण्ड AB खींचिए। रेखाखण्ड के A बिन्दु को केन्द्र मानकर एक चाप लगाइए जो रेखाखण्ड AB को P Rk’ बिन्दु पर काटता है। अब बिन्दु Pको केन्द्र मानकर पहले चाप पर एक और चाप लगाते हैं जो पहले चाप को Q बिन्दु पर काटता है। Qको केन्द्र मानकर उसी चाप को एक बार और लगाइए जो पहले चाप को R बिन्दु पर काटता है।

अब Q तथा R को केन्द्र मानकर एक-एक चाप लगाइए जो एक दूसरे को M पर काटते है। A और M को मिलाइए। अतः ∠MAB = 90°

अब AM के बिन्दु 0 तथा रेखाखण्ड AB के बिन्दु Pको केन्द्र मानकर एक-एक चाप लगाइए जो एक दूसरे को N बिन्दु पर काटते हैं।
अतः ∠ MAB = 90°
∴ ∠ NAB = $\frac { 1 }{ 2 }$ ∠ MAB = $\frac { 1 }{ 2 }$ × 90= 45°
अत: समकोण ∠ MAB दो भागों में विभजित हो गया है।

प्रश्न 5.
अपनी अभ्यास पुस्तिका पर एक ∠PQR = 60° बनाइए तथा दूसरा कोण ∠ABC = 45° खींचिए ∠PQR = ∠PQR – ∠ABC हो जाए।
उत्तर :
ज्ञात है – बड़ा ∠PQR तथा छोटा कोण ∠ ABC
रचना करनी है – ∠PQN = ∠PQR – ∠ ABC के बराबर कोण की
रचना – सर्वप्रथम अज्ञात नाप का एक बड़ा ∠PQR तथा एक छोटा ∠ABC खींचिए। अब ∠ABC के बराबर रेखाखण्ड QR पर ∠NQR बनाइए।

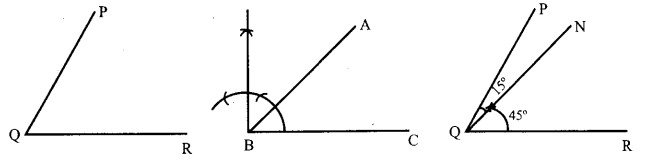
अतः ∠NQR = ∠ABC
∠PQN = ∠PQR – ∠NQR
∠PQN =∠PQR – ∠ABC

अभ्यास 4 (c)

प्रश्न 1.
अपनी अभ्यास पुस्तिका पर दो समान्तर रेखाएँ AB और CD खींचिए। बिन्दु A और C पर क्रमशः 30° और 60° के कोण बनाती हुई रेखाखण्ड AM और रेखाखंड CM बनाइए। ∠AMC का मान ज्ञात कीजिए।
UP Board Solutions for Class 7 Maths Chapter 4 रचनाएँ 11
रचना – सर्वप्रथम दो समान्तर रेखाएँ AB तथा CD खींची। बिन्दु A पर 30° का कोण बनाया तथा बिन्दु C पर 60° का कोण बनाया, जो एक दूसरे को बिन्दु M पर काटते हैं।
नापने पर, 2 AMC = 90°।

प्रश्न 2.
पटरी और परकार की सहायता से एक वर्ग की रचना कीजिए जिसकी प्रत्येक भुजा 5 सेमी है। विकर्ण की लम्बाई को मापकर उसका मान लिखिए।

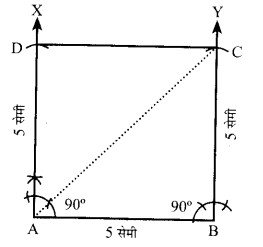
रचना – सर्वप्रथम 5 सेमी का एक रेखाखण्ड AB खींचा। पटरी व परकार की सहायता से बिन्दु A व B का 90° का कोण बनाया। परकार में 5 सेमी की दूरी भर बिन्दु A तथा B से चाप AX को बिन्दु D पर तथा BY को बिन्दु C पर काटता है। CD को मिलाया।
नापने पर, विकर्ण AC = 7.1 सेमी (लगभग)

प्रश्न 3.
4 सेमी माप के रेखाखण्ड AB के अन्त्य बिन्दु A पर ∠BAC=60° की रचना कीजिए। बिन्दु B से AC के समान्तर रेखा खींचिए।
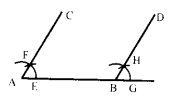
UP Board Solutions for Class 7 Maths Chapter 4 रचनाएँ 13
रचना – सर्वप्रथम एक रेखाखण्ड AB=4 सेमी खींचा। बिन्दु A पर ∠ BAC = 60° पटरी व परकार की सहायता से बनाया। बिन्दु B से AC के समान्तर रेखा खींचने के लिए बिन्दु से 60° का कोण बनाया।
अत: BD, AC के समान्तर रेखा है।

प्रश्न 4.
एक त्रिभुज ABC की रचना कीजिए, जबकि BC=4 सेमी, CA=8 सेमी और AB=6 सेमी। AB के मध्य बिन्दु से BC के समान्तर रेखा खींचिए जो AC को बिन्दु M पर काटे। AM तथा CM की लम्बाई को मापकर लिखिए। क्या AM=CM है?
उत्तर :

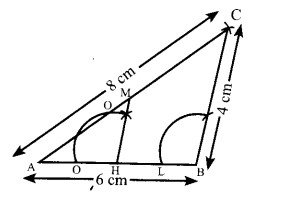
रचना – सर्वप्रथम AB=6 सेमी की एक रेखा खीचीं। बिन्दु A से 8 सेमी की दूरी लेकर एक चाप लगाया तथा बिन्दु B से 4 सेमी की दूरी लेकर दूसरा चाप लगाया, जो पहले चाप को बिन्दु C पर काटता है। अत: ABC अभीष्ट त्रिभुज है। AB का मध्य बिन्दु H लिया। बिन्दु H से ∠ABC के बराबर कोण AHM बनाया। बिन्दु M, AC को समद्विभाजित करता है। मापने पर, AM = CM= 4 सेमी।

अभ्यास 4 (d)

प्रश्न 1.
एक रेखाखण्ड AB खींचिए। इस पर कोई बिन्दु M अंकित कीजिए। M से होकर रेखाखण्ड AB पर एक लम्ब पटरी और परक द्वारा खींचिए।
हल :

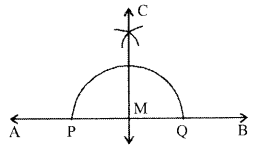
रचना – बिन्दु M से एक चाप लगाया जो AB को Pऔर Q पर काटती है। P से PM से बड़ी त्रिज्या का चाप लगाया। फिर Q से उसी त्रिज्या से दूसरा चाप लगाया। दोनों चाप C पर काटते हैं। बिन्दु M और C को मिलाते हुए आगे बढ़ाया।

प्रश्न 2.
एक रेखाखण्ड PQ खींचिए। कोई बिन्दु R लीजिए जो रेखा PQ पर न हो। R से होकर रेखा PQ पर एक लम्ब खींचिए।
हल :

रचना – बिन्दु R को केन्द्रमानकर उपयुक्त त्रिज्या से एक चाप खींचा जो रेखा PQ को A और B पर काटता है। A को केन्द्र मानकर AB के आधे से अधिक की त्रिज्या लेकर R के विपरीत चाप लगाया। उसी त्रिज्या B से R के विपरीत चाप लगाया। दोनों चाप S पर काटते हैं। बिन्दु R तथा S को मिलाया। यह RS रेखा PQ को C बिन्दु पर काटती है। रेखा RS लम्ब है।

प्रश्न 3.
5 सेमी का एक रेखाखण्ड MN खींचिए। रेखाखण्ड MN पर एक बिन्दु Pलेकर, बिन्दु P से रेखाखण्ड MN पर एक लम्ब खीचिए।
हल :

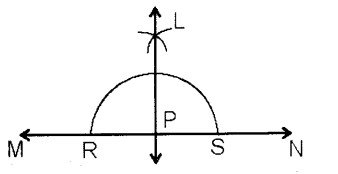
रचना – सर्वप्रथम MN एक रेखाखण्ड खींचा, उस एक बिन्दु P लिया

बिन्दु Pसे एक चाप लगाया, जो रेखाखण्ड MN को R,S बिन्दुओं पर काटता है। R से RP से बड़ी त्रिज्या लेकर चाप लगाया। S से उसी त्रिज्या का दूसरा चाप लगाया। दोनों चाप बिन्दु L पर काटते हैं। बिन्दु L तथा P को मिलाया। अतः LP रेखा MN पर लम्ब है।

दक्षता अभ्यास-4

प्रश्न 1.
चाँदी की सहायता से 30° का कोण खींचिए। अब पटरी और परकार की सहायता से इसे समद्विभाजित कीजिए। प्रत्येक कोण को माप कर सत्यापन कीजिए।
UP Board Solutions for Class 7 Maths Chapter 4 रचनाएँ 18
रचना – सर्वप्रथम एक रेखाखण्ड BC खींचा। बिन्दु B पर चाँदा की। सहायता से 30° का कोण बनाया। शीर्ष B को केन्द्र मानकर किसी त्रिज्या से एक चाप खींचा, जो भुजा BA और BC को क्रमश: N और M बिन्दुओं N P पर काटता है। N और M को केन्द्र मानकर उसी त्रिज्या से चाप लगाए जो ‘ BM C एक-दूसरे को बिन्दु P पर काटते हैं। B और P को मिलाकर D तक बढ़ाया।
मापने पर, 2 DBC = ∠ABD = 15°

प्रश्न 2.
दो रेखाएँ AB और CD खींचिए जो किसी बिन्दू 0 पर प्रतिच्छेदित करती हैं। इस प्रकार बने शीर्षाभिमुख कोण COA और कोण BOD की पटरी परकार की सहायता से समद्विभाजित करके सत्यापित कीजिए कि इनके समद्विभाजक एक ही रेखा में हैं।
UP Board Solutions for Class 7 Maths Chapter 4 रचनाएँ 19
रचना – सर्वप्रथम दो रेखाएँ AB तथा CD खींची, जो बिन्दु 0 पर C Plo, एक-दूसरे को प्रतिच्छेदित करती हैं। ∠COA की समद्विभाजक रेखा OT खींची तथा ∠ BOD की समद्विभाजक रेखा OS खींची।
सत्यापन : मापने पर, 2 SOT = 180° अतः कोणों के समद्विभाजक OT तथा OS एक ही रेखा में हैं।

प्रश्न 3.
एक अधिक कोण ∠PQR तथा एक न्यून कोण ∠ABC खींचिए। इन दोनों के अन्तर के बराबर कोण की रचना कीजिए। बनाए गए कोण की माप बताइए। यह एक न्यूनकोण है या अधिक कोण?
हल :

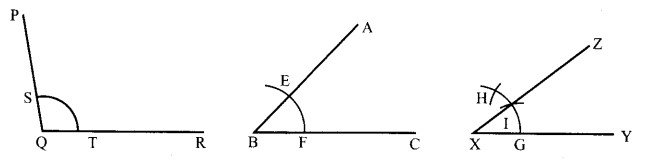
रचना – सर्वप्रथम एक रेखाखण्ड XY खींचा तथा दो कोण ABC तथा PQR दिए हैं। इन दोनों कोणों में B व Q को केन्द्र मानकर दो बराबर क्रिया के चाप लगाए जो क्रमशः AB तथा AC को बिन्दु E तथा F पर तथा क्रमशः PQ तथा QR को बिन्दु S तथा T पर काटते हैं। इसी त्रिज्या को लेकर बिन्दु X से एक चाप लगाया जो XY को बिन्दु G पर काटता है। बिन्दु G को केन्द्र मानकर EF के बराबर दूरी लेकर चाप खींचा, जो पहले चाप को H बिन्दु पर काटता है। बिन्दु H को केन्द्र मानकर ST के बराबर दूरी लेकरे चाप खींचा, जो पहले चाप को बिन्दु I पर काटता है। XI को मिलाकर आगे की ओर बिन्दु Z तक बढ़ाया। कोण ZXY दिए गए कोणों के अन्तर के बराबर कोण होगा।

प्रश्न 4.
पटरी और परकार की सहायता से $7\frac { 1 }{ 2 }$ ° और $22\frac { 1 }{ 2 }$ ° के कोणों की रचना कीजिए।
रचना –

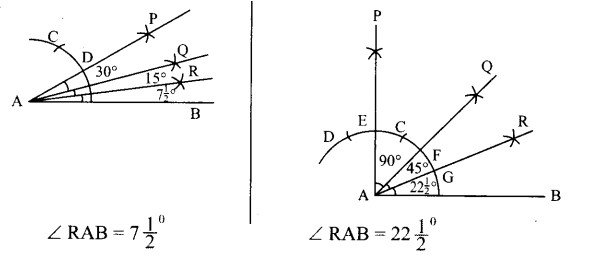
प्रश्न 5.
एक 3 सेमी माप के रेखाखण्ड AB के सिरे A पर लम्ब AC = 3 सेमी खींचिए। बिन्दुओं B,C को मिलाइए। कोणों को मापकर सत्यापित कीजिए कि ∠ABC = ∠ACB = 45°
हल :

सत्यापन-चूँकि दो समान भुजाओं के सामने के कोण बराबर होते हैं। अतः CA ∠ABC = ∠ACB हम जानते हैं कि त्रिभुज के तीनों कोणों का योग = 180°
∴ ∠ABC + ∠ ACB + ∠ CBA = 180°
∠ ABC + ∠ABC + 90° = 180°
2 ∠ ABC = 180° – 90°
∠ABC = $\frac { 90 }{ 2 }$ = 45°
∠ABC = 2 ACB = 45०

प्रश्न 6.
एक 5 सेमी माप का रेखाखण्ड AB खींचिए। बिन्दुओं A और B पर क्रमशः 60° और 120° के कोणों की रचना पटरी और परकार की सहायता से खींचिए। इन कोणों के अर्धक खींचिए। मान लीजिए कि ये बिन्दु C पर मिलते हैं। ∠ACB को नापिए।
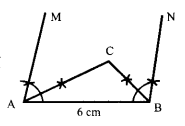
UP Board Solutions for Class 7 Maths Chapter 4 रचनाएँ 23
रचना : सर्वप्रथम 5 सेमी लम्बाई का एक रेखाखण्ड AB खींचा। बिन्दु A पर पटरी तथा परकार की सहायता से 60° का ∠MAB बनाया तथा बिन्दु B पर पटरी तथा परकार की सहायता से 120° का कोण ∠ NBA बनाया। ∠MAB तथा ∠ NAB का अर्धक किया जो एक-दूसरे को बिन्दु C पर काटते हैं।
नापने पर, ∠ACB = 90°

प्रश्न 7.
किसी त्रिज्या का एक वृत्त खींचिए। इसमें दो जीवा PQ और QR लीजिए। इन जीवाओं के लम्बर्धक खींचिए। इनके प्रतिच्छेद बिन्दु C से P, Q और R को मिलाइए। रचना द्वारा सत्यापित कीजिए कि बिन्दु C वृत्त का केन्द्र है।
UP Board Solutions for Class 7 Maths Chapter 4 रचनाएँ 24
रचना – सर्वप्रथम किसी भी त्रिज्या का एक वृत्त खींचा। वृत्त की दो जीवाएँ PQ तथा QR खींची। जीवाओं के लम्बार्धक करने पर ये एक-दूसरे को C बिन्दु पर काटते हैं। C को P, Q, R से मिलाया। नापने पर, CP = CQ = CR अतः बिन्दु C वृत्त का केन्द्र है।

प्रश्न 8.
एक त्रिभुज PQR खींचिए। इनके अन्तः कोणों के समद्विभाजक खींचिए। क्या इनके अर्द्धक एक ही बिन्दु पर मिलते हैं?

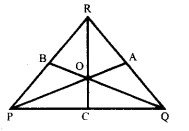
रचना – सर्वप्रथम एक त्रिभुज PQR बनाया। फिर इसके अन्त:कोणों के समद्विभाजक क्रमश: AP, BQ तथा CR किए जो एक-दूसरे को बिन्दु पर मिलते हैं।

प्रश्न 9.
एक त्रिभुज ABC खींचिए। इनकी भुजाओं के लम्ब समद्विभाजक खींचिए। क्या ये एक ही बिन्दु पर मिलते हैं?
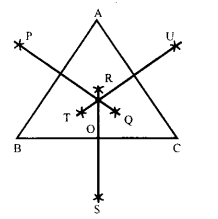
UP Board Solutions for Class 7 Maths Chapter 4 रचनाएँ 26
रचना – सर्वप्रथम एक त्रिभुज ABC बनाया। फिर इसकी भुजाओं , AB, BC तथा CA के लम्बार्द्धक क्रमश: PQ, RS तथा TU खींचे, जो एक-दूसरे को बिन्दु 0 पर काटते हैं।

प्रश्न 10.
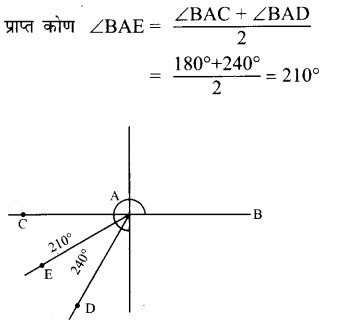
पटरी और परकार की सहायता से 210° के कोण की रचना कीजिए।
रचना – सर्वप्रथम एक रेखाखण्ड AB खींचा। रेखा AB के A बिन्दु पर 180° व 240° के क्रमश: कोण BAC और कोण BAD बनाए, फिर कोण BAC तथा कोण BAD को समद्विभाजित किया।

प्रश्न 11.
एक रेखाखण्ड AB खींचिए। ABके बाहर कोई बिन्दु O लीजिए। O से होकर जाने वाली AB के समान्तर रेखा PQ खींचिए। O को बिन्दु B से मिलाइए। रेखा PQ पर कोई अन्य बिन्दु S लीजिए। बिन्दु S से होकर जाने वाली रेखा OB के समान्तर एक रेखा खींचिए जो PQ को बिन्दु T पर काटे। समान्तर रेखाओं के इन युग्मों से कौन-सी आकृति बनती है।
हल :

1. सर्वप्रथम रेखाखण्ड ABखींचा। AB के बाहर कोई बिन्दु 0 लिया 0 से B को मिलाया तथा AB के समान्तर रेखा PQ खींची।
2. रेखाखण्ड AB पर कोई अन्य बिन्दु S लिया बिन्दु S पर ∠ABD के बराबर कोण बनाती हुई रेखा खींची जो PQ को T पर काटती है। ST को मिलाया जो कि OB के समान्तर रेखा है।
3. इस प्रकार आकृति SBOT एक समान्तर चतुर्भुज बनती है।

Leave a Reply Cancel reply