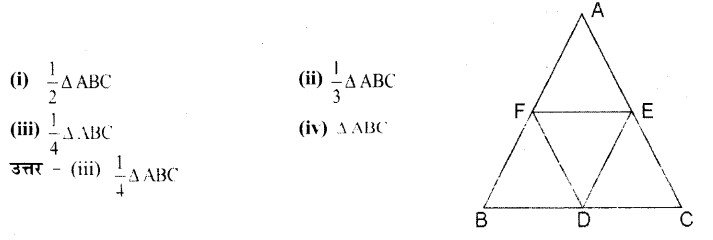अभ्यास 5 (a)

प्रश्न 1.
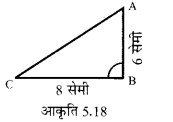
आकृति 5.18 में ∠B समकोण है, भुजा CA की माप होगी?
(i) 5 सेमी
(ii) 10 सेमी
(iii) 8 सेमी
(iv) 6 सेमी
हल :
CA² = AB² + BC² = 6² + 8² = 36+ 64 = 100 = 10²
CA = 10 सेमी (ii)

प्रश्न 2.
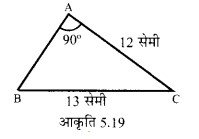
आकृति 5.19 ∠A समकोण हो, तो AB की माप होगी?
(i) 25 सेमी
(ii) 13 सेमी
(ii) 5 सेमी।
(iv) 12 सेमी
हल :
AB² = BC² – CA ² = 13² – 12²
= 169- 144 = 25 = 5²
AB = 5 सेमी (iii)

प्रश्न 3.
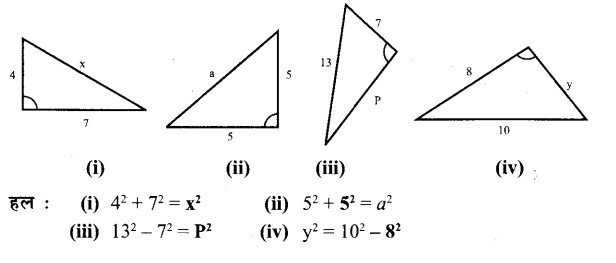
निम्नलिखित आकृतियों में समकोण त्रिभुजों को देखकर अपनी अभ्यास पुस्तिका में रिक्त स्थानों की पूर्ति कीजिए

प्रश्न 4.
∆ABC में ∠ABC समकोण है। यदि AB = 7 सेमी और BC = 24 सेमी, तो CA की लम्बाई ज्ञात कीजिए।
हल :
समकोण त्रिभुज ABC में,

प्रश्न 5.
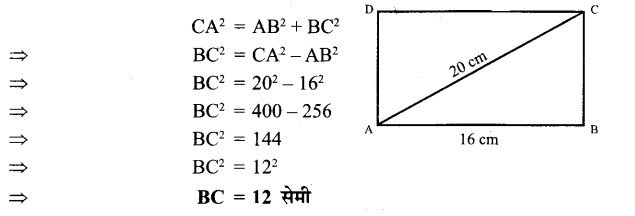
आयत ABCD में विकर्ण CA = 20 सेमी और AB = 16 सेमी। BC की लम्बाई ज्ञात कीजिए।
हल :
समकोण त्रिभुज ABC में,

प्रश्न 6.
65 डेसीमी लम्बी सीढ़ी को दीवार से 25 डेसीमी हटाकर लगाया गया है, दीवार के आधार से सीढ़ी के ऊपरी सिरे की ऊँचाई ज्ञात कीजिए।

हल :
माना दीवार के आधार से सीढी के ऊपरी सिरे की ऊँचाई = h डेसीमी समकोण त्रिभुज ABC में,

प्रश्न 7.
26 मीटर लम्बा एक तार है। उसका एक सिरा 24 मीटर ऊँचे खम्भे के ऊपरी सिरे से बँधा है। और दूसरा जमीन में गड़ा है। जमीन पर खम्भे और तार के निचले सिरे के बीच की दूरी ज्ञात कीजिए।

प्रश्न 8.
निम्नलिखित पाइथागोरियन त्रिक हैं। प्रत्येक से तीन-तीन पाइथागोरियन त्रिक बनाइए।
(i) 3,4,5
(ii) 5, 12, 13
(iii) 8, 15, 17
हल :
(i) 3, 4, 5 पाइथागोरियन त्रिक है।
3, 4, 5 को 2 से गुणा करने पर,
(3 × 2, 4 × 2, 5 × 2) अर्थात् 6, 8, 10 भी पाइथागोरियन त्रिक होंगे।
3, 4, 5 को 3 गुणा करने पर,
(3 × 3, 4 × 3, 5 × 3) अर्थात् 9, 12, 15 भी पाइथागोरियन त्रिक होंगे।
3, 4, 5 को 4 गुणा करने पर,
(3 × 4, 4 × 4, 5 × 4) अर्थात् 12, 16, 20 भी पाइथागोरियन त्रिक होंगे।

(ii) (5, 12, 13) के पाइथागोरियन त्रिक हैं।
= (2×5, 2 x 12, 2 x 13); तथा (3 x 5, 3 x 12,3 x 13)
(4 x 5, 4 x 12, 4 x 13) = (10, 24, 26); (15, 36, 39) तथा (20, 48, 52)

(iii) (8, 15, 17) के पाइथागोरियनु त्रिक हैं।
= (2 × 8, 2 × 15, 2 × 17); (3 × 8, 3 × 15, 3 × 17) तथा (4 × 8, 4 × 15, 4 × 17)
= (16, 30, 34); (24, 45, 51) तथा (32, 60, 68)

प्रश्न 9.
निम्नलिखित में पाइथागोरियन त्रिक छाँटकर लिखिएः
(i) 5, 12, 13
(ii) 7,8, 15
(iii) 6,7,8
(iv) 8, 15, 17
(v) 3,4,5
हल :

अभ्यास 5 (b)

प्रश्न 1.
त्रिभुज ABC की रचना कीजिए जिसकी भुजा BC=6.0 सेमी ∠B=50°तथा CA+AB=8.0 सेमी
हल :
दिया है A ABC में रेखाखण्ड BC = 6 सेमी ∠B = 50 तथा ∠A + AB = 8 सेमी
रचना करनी है – ∆ ABC की।
रचना-

1. सर्वप्रथम रेखाखण्ड BC=6 सेमी खींचा।
2. बिन्दु B पर 50°का कोण बनाती हुई रेखा BY खींची।
3. रेखा BY से दो भुजाओं का योग (CA+AB=8 सेमी) का रेखाखण्ड BD खींचा। बिन्दु D को C से मिलाया।
4. रेखाखण्ड CD का लम्बार्द्धक खींचा जो कि BD को A पर प्रतिच्छेद करता है। A को C से मिलाया।
5. यही AABC अभीष्ट त्रिभुज है।
   

प्रश्न 2.
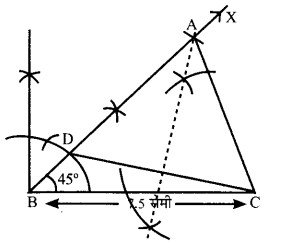
∆ABC की रचना कीजिए जिसमें BC = 7.5 सेमी, ∠B = 45° तथा AB – CA = 2.0 सेमी
हल :
दिया है ∆ABC में रेखाखण्ड BC=7.5 सेमी 2B = 45° तथा AB – CA = 2 सेमी
रचना करनी है – ∆ ABC की
रचना –

1. र्वप्रथम रेखाखण्ड BC = 7.5 सेमी खींचा।
2. बिन्दु B पर परकार व पटरी की सहायता से 45° का। कोण बनाती हुए रेखा BX खींची।
3. रेखा BXसे AB-CA=2 सेमी का रेखाखण्ड। BD खींचा।
4. बिन्दु D से C को मिलाया।
5. रेखाखण्ड CD का लम्बार्द्धक खींचा जो BX को A पर काटता है। CA को मिलाया।
6. यही ∆ABC अभीष्ट त्रिभुज है।
   

प्रश्न 3.
∆ABC की रचना कीजिए जिसमें BC = 5 सेमी, ∠B = 50° तथा AC – AB = 2 सेमी
हल :
दिया है A ABC में रेखाखण्ड BC=5 सेमी ∠B= 50° तथा AC-AB=2 सेमी
रचना करनी है – ∆ ABC की।
रचना –

1. सर्वप्रथम रेखाखण्ड BC=5 सेमी खींचा।
2. बिन्दु B पर 50° का कोण बनाती हुई रेखा BX खींची तथा इसे B की तरफ नीचे बढ़ाते हुए रेखा BY खींचीं।
3. रेखा BY से AC-AB=2 सेमी का रेखाखण्ड BD खींचा।
4. बिन्दु D से C को मिलाया।
5. रेखाखण्ड CD का लम्बार्द्धक खींचा जो रेखा BX को A पर काटता है। CA को मिलाया।
6. यही ∆ABC अभीष्ट त्रिभुज है।
   

अभ्यास 5 (c)

प्रश्न 1.
नीचे दी गई भुजाओं और कोणों से त्रिभुज खींचकर उनके शीर्षलम्ब खींचिए तथा जाँच कीजिए कि प्रत्येक त्रिभुज के शीर्षलम्ब संगामी हैं।
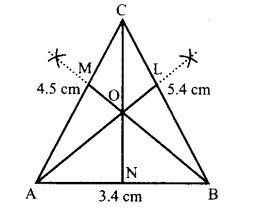
(i) 3.4 सेमी. 5.4 सेमी. 4.5 सेमी;
(ii) दो भुजाएँ 6 सेमी और 4.5 सेमी तथा इनके बीच का कोण 120°;
(iii) दो भुजाएँ 5 सेमी और 4 सेमी तथा इनके बीच की कोण 90°;
(iv) दो कोण 65° तथा 80° और बीच की भुजा 5 सेमी।।

(i) रचना – सर्वप्रथम दी हुई भुजाओं की माप से A ABC * बनाया। शीर्ष A से ALL BC खींचा। शीर्ष B से BM 1 AC खींचा। शीर्ष C से CN 1 AB खींची। ∆ABC के तीनों शीर्षलम्ब AL, BM और CN एक ही बिन्दु 0 से होकर जाते हैं। अत: प्रत्येक त्रिभुज के शीर्षलम्ब संगामी हैं।

नोट : विद्यार्थी प्रश्न 1 का खंड
(ii), (iii) व
(iv) की रचना खंड
(i) की तरह अपने अध्यापक की सहायता से स्वयं करें।

प्रश्न 2.
एक समद्विबाहु त्रिभुज ABC खींचिए, जिसमें AB=AC, शीर्ष A से शीर्षलम्ब AL खींचिए। मापकर बताइए कि निम्नलिखित कथन सत्य हैं या नहीं।
हल :

प्रश्न 3.
AABC में ∠C समकोण है। इस त्रिभुज का बिना शीर्षलम्ब खींचे तथा केन्द्र बताइए।
हल :
AABC में ∠C समकोण है अतः त्रिभुज का लम्बकेन्द्र, शीर्ष लम्ब AC तथा BC का प्रतिच्छेद बिन्दु C होगा।

अभ्यास 5(d)

प्रश्न 1.
निम्नलिखित कथनों को अपनी अभ्यास-पुस्तिका में लिखकर रिक्त स्थानों की पूर्ति कीजिए: ( पूर्ति करके)
उत्तर :

• त्रिभुज की माध्यिका वह रेखाखण्ड है जो इसके किसी शीर्ष को सम्मुख भुजा के मध्यबिन्दु से मिलाती है।
• किसी त्रिभुज की माध्यिकाएँ संगामी होती हैं।
• त्रिभुज की माध्यिकाएँ जिस बिन्दु पर मिलती हैं उसे केन्द्रक कहते हैं।
  

प्रश्न 2.
एक समद्विबाहु त्रिभुज ABC खींचिए, जिसमें AB = AC माध्यिका AD खींचिए। नापकर बताइए कि निम्नलिखित कथन सत्य हैं या नहीं।
उत्तर :
सर्वप्रथम एक समद्विबाहु त्रिभुज ABC, खींचा, जिसमें AB = AC एवं AD माध्यिका खींची। नापने पर,

• AD, BC पर लम्ब है। ( सत्य)
• AD, 2A को समद्विभाजित करता है। ( सत्य)
• AD, BC का लम्ब समद्विभाजक है। ( सत्य)

प्रश्न 3.
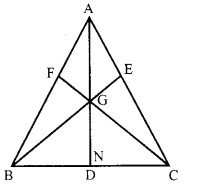
AD, BE और CF किसी ∆ABC की माध्यिकाएँ हैं और G इसका केन्द्रक है। यदि BE=CF, तो ∆GBC किस प्रकार का त्रिभुज है? आकृति बनाकर देखिए।
(i) विषमबाहु
(ii) समद्विबाहु
(iii) समबाहु
हल :
(ii) समद्विबाहु

अभ्यास 5 (e)

प्रश्न 1.
एक रेखाखण्ड AB लेकर उसकी लम्ब समद्विभाजक रेखा खींचिए। पर कोई बिन्दु P लेकर PA और PB को नापिए। क्या PA और PB बराबर हैं?
हल :
हाँ, PA और PB बराबर हैं।

प्रश्न 2.
एक समकोण त्रिभुज ABC खींचिए, जिसमें ∠C समकोण हो। AB का मध्य बिन्दु 0 ज्ञात कीजिए। केन्द्र O और त्रिज्या OA वाला एक वृत्त खींचिए। क्या यह C से होकर जाता है?A ABC के संदर्भ में, बिन्दु’O को क्या कहते हैं?
हल :
हाँ, केन्द्र 0 और त्रिज्या OA वाला वृत्त C से होकर जाता है। ∆ABC के संदर्भ में, बिन्दु 0 को परिकेन्द्र कहते हैं।

प्रश्न 3.
नीचे दी गई भुजाओं और कोणों से त्रिभुज बनाइए और उनकी भुजाओं के लम्ब समद्विभाजक खींचिए और जाँच कीजिए कि वे संगामी हैं।
(i) 7 सेमी, 5 सेमी और 4 सेमी
(ii) 6 सेमी तथा भुजा पर बने कोण 90° और 30°
(iii) 4.5 सेमी, 2.5 सेमी, बीच कोण 105°

(i) रचना – सर्वप्रथम दी गई भुजा व कोणों की माप से त्रिभुज ABC बनाया। भुजा AB, BC तथा AC के लम्ब समद्विभाजक क्रमशः l, m तथा n खींचे। ये लींब समद्विभाजक एक-दूसरे को बिन्दु 0 पर काटते हैं। अतः ये संगामी हैं।
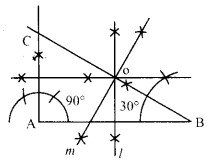
(ii) रचना – सर्वप्रथम 6 सेमी की एक रेखा AB खींची। अब बिन्दु A पर 90° का कोण और बिन्दु B पर 30° का कोण बनाया A और B के किरणों को बढ़ाया जो एक-दूसरे को बिन्दु C पर काटती हैं। अब AB,BC और AC के लम्ब समद्विभाजक खींचे। ये लम्ब समद्विभाजक एक-दूसरे को बिन्दु पर काटते हैं। अतः ये संगामी हैं।
(iii) रचना – विद्यार्थी
(ii) की भाँति अध्यापक की सहायता से स्वयं करें।

अभ्यास 5 (f)

प्रश्न 1.
नीचे दी गई भुजाओं तथा कोणों से त्रिभुज बनाइए और उनके कोणों के समद्विभाजक खींचकर जाँच कीजिए कि क्या वे संगामी हैं।
(i) 3.4 सेमी, 4 सेमी तथा 2.5 सेमी
(ii) 4.6 सेमी, 3.5 सेमी तथा बीच का कोण 120°
(iii) 5 सेमी, 4 सेमी तथा 2.5 सेमी।

(i) रचना – सर्वप्रथम दी गई भुजाओं की माप से ∆ABC बनाया। ∠A, ∠B और ∠C के समद्विभाजक खींचे। ये एक-दूसरे के बिन्दु 0 पर काटते हैं।
अतः ये संगामी हैं।
(ii) रचना – सर्वप्रथम दी गई भुजा व कोणों की माप से त्रिभुज ∆ABC बनाया। ∠A, ∠B और ∠C के समद्विभाजक खींचे। ये एक-दूसरे के बिन्दु 0 पर काटते हैं। अतः ये संगामी हैं।
(iii) रचना – छात्र खंड
(i) की भाँति स्वयं करें।

प्रश्न 2.
एक समबाहु ∆ABC खींचिए और उसका केन्द्र ज्ञात कीजिए। यह भी ज्ञात कीजिए कि इसके परिकेन्द्र, लम्बकेन्द्र व केन्द्रक इसके अन्तः केन्द्र पर संपाती हैं।
रचना – सर्वप्रथम एक समबाहु त्रिभुज ABC खींचा। ∠A, ∠ B तथा ∠C के समद्विभाजक किए। जो त्रिभुज में बिन्दु 0 से होकर जाते हैं। बिन्दु 0 समद्विबाहु त्रिभुज का अन्त: केन्द्र है। चूँकि समबाहु त्रिभुज में अन्त: केन्द्र, परिकेन्द्र, लम्बकेन्द्र व केन्द्रक एक ही बिन्दु होता है। अतः समबाहु त्रिभुज के परिकेन्द्र, लम्बकेन्द्र व केन्द्रक इसके अन्तः केन्द्र पर संपाती हैं।

प्रश्न 3.
पाश्र्व चित्र में ∆ABC समद्विबाहु त्रिभुज है, इसमें AB= AC है, AP, ∠A का अर्धक है। यह रेखाखण्ड AP, BC का लम्बार्धक है या नहीं। चित्र खींचकर और नापकर बताइए।
रचना – सर्वप्रथम एक समद्विबाहु त्रिभुज ABC खींचा, जिसमें AB = ACI ∠A का अर्धक AP खींचा। भुजा BC का लम्बार्धक खींचा, जो अर्धक AP से मिलता है। अत: रेखाखण्ड AP, BC का लम्बार्धक है।

अभ्यास 5 (g)

प्रश्न 1.
रिक्त स्थानों की पूर्ति कीजिए ( पूर्ति करके)
हल :

• समकोण त्रिभुज का परिकेन्द्र कर्ण पर स्थित होता है।
• अधिक कोण त्रिभुज का परिकेन्द्र त्रिभुज के बाह्य क्षेत्र में स्थित होता है।
• न्यूनकोण त्रिभुज का परिकेन्द्र त्रिभुज अन्तः क्षेत्र में स्थित होता है।

प्रश्न 2.
एक त्रिभुज ABC खींचिए जिसमें AB=3 सेमी, BC-4 सेमी और AC=5 सेमी। इस त्रिभुज का परिकेन्द्र ज्ञात कीजिए।
रचना – सर्वप्रथम दी गई नाप के अनुसार एक त्रिभुज ABC खींचा। भुजा AB, BC तथा AC के लम्बार्धक खींचे, जो एक-दूसरे को बिन्दु 0 पर काटते h b हैं। अतः बिन्दु 0 त्रिभुज का परिकेन्द्र है, जो त्रिभुज के कर्ण पर स्थित है।

प्रश्न 3.
एक अधिक कोण त्रिभुज ABC बनाइए जिसका कोण B अधिक कोण हो, इस त्रिभुज का परिकेन्द्र ज्ञात कीजिए।
रचना – सर्वप्रथम किसी भी नाप का एक अधिककोण त्रिभुज बनाया, जिसका कोण B अधिक कोण है। भुजा AB तथा BC के लम्बार्धक खींचे, जो एक-दूसरे को बिन्दु 0 पर काटते हैं। अतः बिन्दू 0 त्रिभुज ABC को परिकेन्द्र है।

अभ्यास 5 (h)

प्रश्न 1.
एक∆ABC बनाइए, जिसका ∠Bअधिक कोण हो। इस त्रिभुज का लंबकेन्द्र ज्ञात कीजिए।
रचना – सर्वप्रथम एक त्रिभुज ABC बनाया, जिसमें B अधिक कोण है। त्रिभुज के शीर्ष A तथा C से शीर्षलम्ब खींचे, जो एक-दूसरे को त्रिभुज के बाहर बिन्दु 0 पर काटते हैं। अतः बिन्दु 0 त्रिभुज का लम्ब केन्द्र है, जो त्रिभुज के बाह्य क्षेत्र में स्थित है।

प्रश्न 2.
न्यूनकोण त्रिभुज ABC बनाइए तथा इसका लम्बकेन्द्र ज्ञात कीजिए। यह भी बताइए कि इस त्रिभुज का लम्बकेन्द्र त्रिभुज के अन्तः क्षेत्र में स्थित है अथवा बाह्य क्षेत्र में।
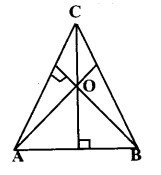
रचना – सर्वप्रथम एक न्यूनकोण त्रिभुज ABC बनाया। त्रिभुज के शीर्ष A,B तथा C से शीर्षलम्बे खींचे, जो एक-दूसरे को बिन्दु 0 पर काटते हैं। अतः बिन्दु 0 त्रिभुज का लम्बकेन्द्र है, जो त्रिभुज के अन्तः क्षेत्र में स्थित है।

अभ्यास 5 (i)

प्रश्न 1.
समकोण त्रिभुज ABC में ∠B समकोण है। AB = 3 सेमी, BC=4 सेमी। इस त्रिभुज की रचना कर इसका केन्द्रक ज्ञात कीजिए।
रचना – सर्वप्रथम दी गई नाप के अनुसार एक समकोण त्रिभुज ABC FN बनाया। AB, BC तथा AC के मध्यबिन्दु क्रमशः F, D, E ज्ञात किए। त्रिभुज की माध्यिकाएँ AD, BE तथा CF खींची। तीनों माध्यिकाएँ एक-दूसरे को बिन्दु G पर काटती हैं। अतः बिन्दु G त्रिभुज का केन्द्रक है।

प्रश्न 2.
एक त्रिभुज की माध्यिकाएँ क्रमशः 6 सेमी, 9 सेमी और 12 सेमी लम्बी है। इस त्रिभुज के केन्द्रक द्वारा माध्यिकाओं के विभाजित भाग ज्ञात कीजिए।
रचना – त्रिभुज का माध्यिकाएँ AD = 6 सेमी, BE = 9 सेमी, CF = 12 सेमी हम जानते हैं कि त्रिभुज का केन्द्रक माध्यिकाओं को 2:1 के अनुपात में विभाजित करती है।

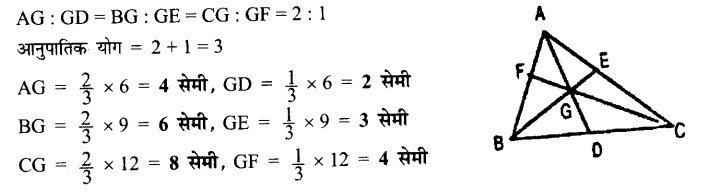
अभ्यास 5 (j)

प्रश्न 1.
आकृति 5.50 में दो त्रिभुज ABC और PQR समरूप हैं। इनकी भुजाओं की लम्बाइयाँ सेमी में अंकित है।x और y ज्ञात कीजिए।

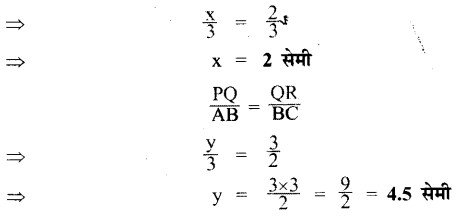
प्रश्न 2.
यदि किसी त्रिभुज ABC और त्रिभुज PQR में उनकी भुजाएँ क्रमशः AB = 3 सेमी, BC=5 सेमी, CA=4 सेमी तथा PQ=7 सेमी, PR=6 सेमी, QR=8 सेमी है, तो त्रिभुज समरूप हैं या नहीं?
हल :
दो त्रिभुज समरूप होंगे यदि,

प्रश्न 3.
आकृति 5.51 में त्रिभुज ABC और त्रिभुज PQR समरूप हैं। त्रिभुज PQR की शेष भुजाओं को ज्ञात कीजिए।

प्रश्न 4.
त्रिभुज ABC में MN, BC के समान्तर ∆ABC के शेष कोणों की माप बताइए। क्या त्रिभुज

प्रश्न 5.
उपर्युक्त आकृति 5.53 में, यहि M तथा N क्रमशः AB और AC भुजाओं के मध्य बिन्द हों, तो भुजा BC और MN का अनुपात ज्ञात कीजिए।
हल :

प्रश्न 6.
हो समान्तर रेखाखण्ड AB और CD खींचिए। A को D से और B को C से मिलाइए। मान लीजिए कि वे एक-दूसरे को बिन्दु 0 पर काटती हैं। क्या त्रिभुज OAB और त्रिभुज OCD समरूप होंगे?

प्रश्न 7.
क्या आकृति 5.54 में ABC त्रिभुज और त्रिभुज PRQ समरूप हैं? यदि हाँ, तो कारण बताइए।

प्रश्न 8.
20 मी = 1 सेमी मानकर एक खेत का आकार आकृति 5.55 में दर्शाया गया है। 40 मी = 1 सेमी मानकर खेत का नया आकार अपनी अभ्यास पुस्तिका पर दर्शाइए।

हल :
चित्र में पैमाना 20 मीटर = 1 सेमी मानकर खेत का आकार प्रदर्शित किया गया है। यदि पैमाना : 40 मीटर = 1 सेमी माना जाए तो खेत के नए आकार में 5 सेमी वाली भुजा 2.5 सेमी, 12 सेमी वाली भुजा 6 सेमी तथा 13 सेमी वाली भुजा 6.5 सेमी होगी। अत: खेत के नए आकार संगत भुजाएँ पहली भुजाओं की आधी होंगी।

अभ्यास 5 (k)

प्रश्न 1.
यदि किसी त्रिभुज ABC की भुजाओं में 4:4:5 का अनुपात हो, तो उनके समरूप एक त्रिभुज की रचना कीजिए। जिसका आधार 7 सेमी हो।।
हल :
दिया है- ∆ABC जिसकी भुजाओं में अनुपात 4:4:5 है।
रचना करनी है- ∆ABC के समरूप ∆PQR की।
1. A की भुजाओं में अनुपात 4:4:5 है। इस अनुपात में 2 से गुणा करने पर क्रमश 8 सेमी, 8 सेमी तथा 10 सेमी होगी।

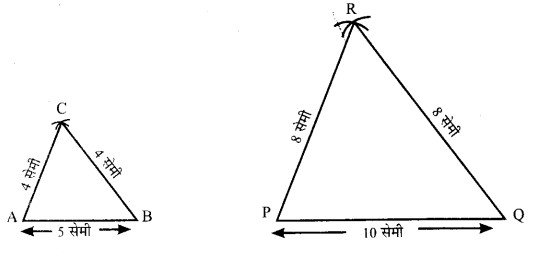
2. अब 6 सेमी, 8 सेमी तथा 10 सेमी की भुजाओं का APQR बनाया।
3. रेखाखण्ड PQ= 10 सेमी खींचा ∠A=∠P तथा ∠B=∠Q बनाती हुई रेखाएँ खींची जोकि एक दूसरे को बिन्दु R पर काटती है। यही APQRAABC को समरूप A है।

प्रश्न 2.
यदि किसी त्रिभुज ABCकी भुजाओं में 3:4:5 का अनुपात हो, तो उनके समरूप एक त्रिभुज की रचना कीजिए। जिसका आधार 7 सेमी हो।
हल :
दिया है – ∆ABC जिसकी भुजाओं में अनुपात 3:4:5 है।
रचना करनी है – ∆ABC के समरूप ∆PQR की ।

1. ∆ की भुजाओं में अनुपात 3:4:5 है। इस अनुपात में 2 से गुणा करने पर क्रमश 6 सेमी, 8 सेमी तथा 10 सेमी होगी।
   
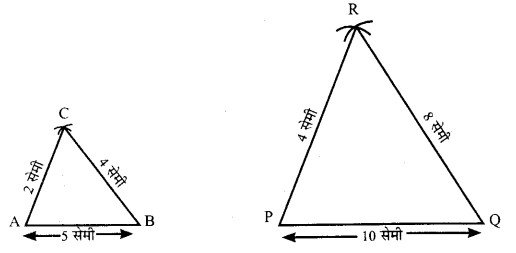
2. अब 6 सेमी, 8 सेमी तथा 10 सेमी की भुजाओं का ∆PQR बनाया।
3. रेखाखण्ड PQ= 10 सेमी खींचा ∠A = ∠P तथा ∠B = ∠Q बनाती हुई रेखाएँ खींची जोक एक दूसरे को बिन्दु R पर काटती है। यही ∆PQR ∆ABC को समरूप ∆ है।

प्रश्न 3.
यदि किसी त्रिभुज ABC की भुजाओं में 2:4:5 को अनुपात हो तो, उनके समरूप एक त्रिभुज की रचना कीजिए। जिसको आधार 3 सेमी हो।।
हल :
दिया है – ∆ABC जिसकी भुजाओं में अनुपात 2:4:5 है।
रचना करनी है – ∆ABC के समरूप ∆PQR की

1. A की भुजाओं में अनुपात 2:4:5 है। इस अनुपात में 2 से गुणा करने पर क्रमश 4 सेमी, 8 सेमी तथा 10 सेमी होगी।
   
2. अब 4 सेमी, 8 सेमी तथा 10 सेमी की भुजाओं का ∆PQR बनाया।
3. रेखाखण्ड PQ= 10 सेमी खींचा ∠A=∠P तथा ∠B=∠Q बनाती हुई रेखाएँ खींची जोकि एक दुसरे को बिन्द R पर काटती है। यही ∆PQR ∆ABC का समरूप A है।

दक्षता अभ्यास 5

प्रश्न 1.
समकोण त्रिभुज ABC में ∠B = 90°, AB = 6.0 सेमी, AC= 10 सेमी, तो BC की माप होगीः
(i) 6 सेमी
(ii) 10 सेमी
(iii) 8 सेमी
(iv) इनमें से कोई नहीं

हलः
BC² = AC² – AB² = 10² – 6²
100 – 36 = 64 = 8²
BC = 8 सेमी (iii)

प्रश्न 2.
एक आयताकार मैदान की लम्बाई 24 मीटर, चौड़ाई A 24 m 10 मीटर है। इस आयताकार मैदान का विकर्ण होगा
(i) 26 मी
(ii) 29 मी
(iii) 20 मी
(iv) 24 मी

हलः
AD² = AB² + BD² = 24² + 10²
= 576 + 100 = 676 = 26²
AD = 26 मी (i)

प्रश्न 3.
एक सर्वेक्षक (Surveyor) बिन्दु A और B के बीच की दूरी ज्ञात करना चाहता है किन्तु वह A से B तक सीधा नहीं पहुँच सकता, अतः वह चित्रानुसार एक समकोण त्रिभुज बनाता है जिसमें AC=21 मी, BC=35 मी, AB कितना लम्बा है?

प्रश्न 4.
बिन्दु A और B एक झील के विपरीत किनारे हैं। एक सर्वेक्षक A और B के बीच की दूरी ज्ञात करने के लिए आकृति 2.46 के अनुसार एक समकोण त्रिभुज ADC बनाता है। A से बिन्दु B के बीच की दूरी कितनी है, जबकि BC= 12 मीटर है।
हल :
समकोण त्रिभुज ADC में,

प्रश्न 5.
एक सड़क के दोनों किनारों पर दो मकान आमने-सामने हैं। 50 मी लम्बी सीढ़ी का एक सिरा सड़क के एक ओर स्थित मकान की दीवार पर 48 मी ऊँचाई तक पहुँचता है तथा दूसरे किनारे वाले मकान की दीवार पर यह केवल 14 मी ऊँचाई तक पहुँचता है। सड़क की चौड़ाई ज्ञात कीजिए।
(संकेत : चित्रानुसार सड़क की चौड़ाई BD = BC + CD)

प्रश्न 6.
उस त्रिभुज का नाम बताइए जिसके परिकेन्द्र और अन्तः बिन्दु एक ही होते हैं।
हल :
समबाहु त्रिभुज में परिकेन्द्र और अन्तः केन्द्र एक ही होते हैं।

प्रश्न 7.
3,4,5 पाइथागोरियन त्रिक है। दिखाइए कि 15, 20, 25 भी पाइथागोरियन त्रिक है।
हल :
(25)² = (15)² + (20)²
25 × 25 = 15 × 15 + 20 × 20
625 = 225 + 400
या 625 = 625
अतः 15, 20, 25 भी पाइथागोरियन त्रिक है।

प्रश्न 8.
एक त्रिभुज ABC की रचना कीजिए, जिसका आधार 7 सेमी, ∠ B= 60° तथा दो भुजाओं का योग 9 सेमी है।
हल :

1. सर्वप्रथम रेखाखण्ड BC=7सेमी खींचा।
2. बिन्दु B पर परकार व पटरी की सहायता से 60°का कोण बनाती हुई , रेखा BY खींची।
3. BY से दो भुजाओं को योग (AB+AC=9cm) का रेखाखण्ड BD खींचा। D को C से मिलाया।
4. DCका लम्बअर्द्धक खींचा जो रेखाखण्ड BD को A पर काटता है। A से C को मिलाया।
5. ∆ABC अभीष्ट त्रिभुज है।
   

प्रश्न 9.
एक ∆ABCकी रचना कीजिए, जिसका एक कोण 120° तथा दो भुजाएँ क्रमशः 5 सेमी तथा 6 सेमी है, तो त्रिभुज का परिकेन्द्र ज्ञात करें।
हल :

1. सर्वप्रथम रेखाखण्ड BC=6 सेमी खींचा।
2. परकार तथा पटरी की सहायता से बिन्दु B पर 120°का कोण बनाती हुई रेखा BYखींची।
3. रेखा BY से रेखाखण्ड AB=5 सेमी खीचा बिन्दु A से C को मिलाया।
   
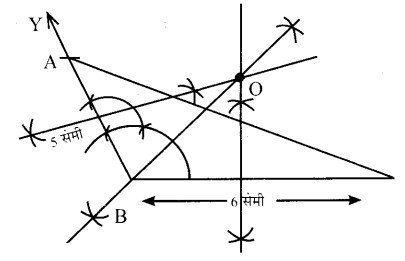
4. रेखाखण्ड AB तथा BC तथा CA का लम्ब अर्द्धक खींचें जो एक दूसरे को ∆ABC के बाह्य बिन्दु O पर मिलते हैं। अतः बिन्दु 0, ∆ABC को परिकेन्द्र है।

प्रश्न 10.
समबाहु त्रिभुज की रचना कीजिए, जिसकी भुजा 6 सेमी हो, तो त्रिभुज का केन्द्रक तथा शीर्ष से केन्द्रक तक की दूरी ज्ञात करें।
हल :

1. सर्वप्रथम रेखाखण्ड BC=6 सेमी खींचा।।
2. बिन्दु B और C को केन्द्र मानकर 6 सेमी त्रिज्या लेकर चाप लगाये जो एक दूसरे को A पर काटते हैं।
3. A से B और C को मिलाया है। अत: ∆ABC अभीष्ट समबाहु A है।
4. ∆ABC के कोण ∠A, ∠B तथा ∠C का समद्विभाजक करते हैं जो कि एक दूसरे को A के केन्द्रक O पर मिलते हैं।
5. अत: OA = OB = OC = 3.5 सेमी
   

प्रश्न 11.
एक त्रिभुज PQR की भुजाओं में 4:5:6 का अनुपात है। इस त्रिभुज के समरूप एक त्रिभुज ABC की रचना कीजिए। जिसको आधार 8 सेमी हो।
हल :
दिया है – ∆PQR जिसकी भुजाओं में अनुपात 4:5:6 है।
रचना करनी है – ∆PQR के समरूप ∆ABC की Q
रचना –

1. A की भुजाओं में अनुपात 4:5:6 है। इस अनुपात में 2 से गुणा करने पर क्रमश 8 सेमी, 10 सेमी तथा 12 सेमी होगी।
2. अब 8 सेमी, 10 सेमी तथा 12 सेमी की भुजाओं का ∆ABC बनाया। C
   
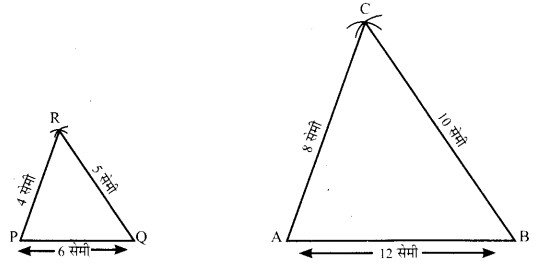
3. रेखाखण्ड AB = 10 सेमी खींचा ∠P =∠A तथा ∠Q=∠B बनाती हुई रेखाएँ खींची जो कि एक दूसरे को बिन्दु C पर काटती है। यही ∆ABC, ∆PQR का समरूप है।

एम०एस०ई० प्रश्न

प्रश्न 12.
किसी त्रिभुज के तल पर स्थित बिन्दु जो त्रिभुज की भुजाओं के बराबर लम्बवत दूरी पर है, वह बिन्दु त्रिभुज का
(i) अन्तः केन्द्र होता है।
(ii) परिकेन्द्र होता है।
(iii) लम्बकेन्द्र होता है।
(iv) केन्द्रक होता है।
उत्तर :
(i) अन्त:केन्द्र होता है।

प्रश्न 13. संलग्न चित्र में DEF का क्षेत्रफल होगा D, E, F भुजाओं के मध्य बिन्दु हैं।