चतुर्भुज की रचनाएँ

अभ्यास 10 (a)

प्रश्न 1.
निम्नांकित चतुर्भुजों के चित्रों के आधार पर क्रमानुसार उनके नाम तथा उनकी भुजाओं, शीर्षों, कोणों और विकर्णो के नाम बताइए।
उत्तर

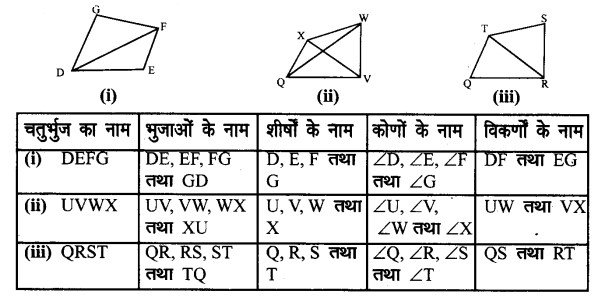
प्रश्न 2.
किसी चतुर्भुज के तीन कोण क्रमशः 75°,95° और 110° हैं। चौथे कोण का मान ज्ञात कीजिए।
उत्तर

प्रश्न 3.
यदि किसी चतुर्भुज के दो कोण 60° तथा 120° के हैं तथा शेष दोनों कोण समान हैं, तो उनके मान ज्ञात कीजिए।
उत्तर

प्रश्न 4.
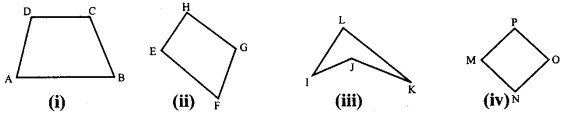
निम्नलिखित चतुर्भुजों की आकृतियाँ खींचिए।
(i) समलम्ब
(ii) उत्तल चतुर्भुज
(iii) अवतल चतुर्भुज
(iv) पतंग (Kite)
उत्तर

अभ्यास 10 (b)

प्रश्न 1.
एक चतुर्भुज ABCD बनाइए, जबकि AB=4.0 सेमी०, BC=6.0 सेमी०, CD=DA= 5.2 सेमी० और AC = 8 सेमी०।।
उत्तर
रचना :

1. सर्वप्रथम रेखाखंड AB = 4.0 सेमी खींचा।
2. फिर A को केन्द्र मानकर 8 सेमी की त्रिज्या का एक चाप खींचा।
3. B को केन्द्र मानकर 6 सेमी की त्रिज्या का दूसरा चाप खींचा जो है पहले चाप को बिन्दु C पर काटता है।
4. AC तथा BC को मिलाया।
5. फिर क्रमशः A को और C को केन्द्र मानकर 5.2 सेमी के चाप खींचे।
6. AD तथ CD को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है।

प्रश्न 2.
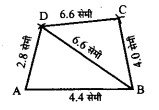
चतुर्भुज ABCD की रचना कीजिए जिसमें AB = 4.4 सेमी, BC=4 सेमी, CD=6.4 सेमी, DA = 2.8 सेमी और BD = 6.6 सेमी, AC की लम्बाई नापकर लिखिए।
उत्तर

1. सर्वप्रथम रेखाखंड AB = 4.4 सेमी खींचा ।
2. फिर A को केन्द्र मानकर 2.8 सेमी की त्रिज्या का एक चाप खींचा। |
3. B को केन्द्र मानकर 6.6 सेमी की त्रिज्या का दूसरा चाप खींचा जो पहले चाप को बिन्दु D पर काटता है।
4. AD तथा BD को मिलाया।
5. फिर B को केन्द्र मानकर 4 सेमी की त्रिज्या का एक चाप खींचा ।
6. फिर D को केन्द्र मानकर 6.4 सेमी की त्रिज्या का दूसरा चाप खींचा जो पहले चाप को बिन्दु C पर काटता है।
7. BC तथा DC को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है। नापने पर, AC = 6 सेमी।

प्रश्न 3.
एक चतुर्भुज PQRS बनाइये, जहाँ PQ = 3 सेमी, QR = 5 सेमी, QS = 5 सेमी, PS = 4 सेमी और SR = 4 सेमी। PR को नापिए।
उत्तर
रचना :

1. सर्वप्रथम रेखाखंड PQ= 3 सेमी खींचा।
2. फिर P को केन्द्र मानकर 4 सेमी की त्रिज्या का एक चाप खींचा।
3. Q को केन्द्र मानकर 5 सेमी की त्रिज्या का दूसरा चाप खचा जो पहले चाप को बिन्दु S पर काटता है।
4. PS तथा QS को मिलाया।
5. फिर Q को केन्द्र मानकर 5 सेमी की त्रिज्या का एक चाप खींचा ।।
6. S को केन्द्र मानकर 4 सेमी की त्रिज्या का दूसरा चाप खींचा जो पहले चाप को बिन्दु R पर काटता है ।
7. QR तथा SR को मिलाया।

अतः PQRS अभीष्ट चतुर्भुज है । नापने पर, PR = 6.3 सेमी

प्रश्न 4.
एक समचतुर्भुज ABCD की रचना कीजिए, जिसकी प्रत्येक भुजा 4.5 सेमी और एक विकर्ण 6.0 सेमी० हो। दूसरे विकर्ण को नापकर लिखिए।
उत्तर
रचना :

1. सर्वप्रथम रेखाखंड AB = 4.5 सेमी खींची। 24.5 सेमी |
2. फिर A को केन्द्र मानकर 6 सेमी की त्रिज्या का एक चाप । खींचा।
3. इसी प्रकार B को केन्द्र मानकर 4.5 सेमी का दूसरा चाप खचा जो पहले चाप को बिन्दु C पर काटता है।
4. AC तथा BC को मिलाया।
5. फिर A तथा C को केन्द्र मानकर 4.5 सेमी० की त्रिज्या के चाप खींचे, जो एक-दूसरे को बिन्दु D पर काटते हैं।
6.  AD तथा DC को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है । नापने पर, BD = 6.7 सेमी – D,

प्रश्न 5.
समान्तर चतुर्भुज ABCD की रचना कीजिए, जहाँ AB = 3.6 सेंमी, BC = 4.2 सेमी और AC = 6.5 सेमी और शेष भुजा नापकर अपनी उत्तर पुस्तिका पर लिखिए।
उत्तर
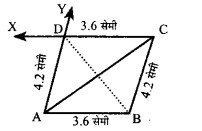
रचना :

1. सर्वप्रथम रेखाखंड AB = 3.6 सेमी खींचा।
2. फिर A से 6.5 सेमी की त्रिज्या को एक चाप खींचा तथा B से 4.2 सेमी की त्रिज्या का दूसरा चाप खींचा जो कि एक-दूसरे को बिन्दु C पर काटते हैं।
3. AC तथा BC को मिलाया।
4.  फिर C से 3.6 सेमी त्रिज्या का एक चाप खींचो तथा A से 4.2 सेमी त्रिज्या का दूसरा चाप खींचा जो कि एक-दूसरे को बिन्दु D पर काटते हैं।
5. AD तथा CD को मिलाया।

अतः ABCD अभीष्ट समान्तर चतुर्भुज है। नापने पर, BD = 4.4 सेमी

अभ्यास 10 (c)

प्रश्न 1.
चतुर्भुज ABCD की रचना कीजिए, जबकि AB = 3.8 सेमी, BC = 3 सेमी, AD = 2.3 सेमी, AC = 4.5 सेमी और BD = 3.8 सेमी। CD की माप नापकर ज्ञात कीजिए।
उत्तर

रचना :

1. सर्वप्रथम रेखाखंड AB = 3.8 सेमी खींचा।
2. फिर A को केन्द्र मानकर 2.3 सेमी की त्रिज्या का एक चाप खींचा।
3. B को केन्द्र मानकर 3.8 सेमी की त्रिज्या का दूसरा चाप है खींचा जो पहले चाप को बिन्दु D पर काटता है। |
4. AD तथा BD को मिलाया।
5. फिर पुनः A को केन्द्र मानकर 4.5 सेमी की त्रिज्या का एक चाप चा।
6. पुनः B को केन्द्र मानकर 3 सेमी की त्रिज्या का दूसरा चाप खींचा जो पहले चाप को बिन्दु C पर काटता है।
7. AC तथा BC को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है। नापने पर, CD = 2.3 सेमी

प्रश्न 2.
चतुर्भुज ABCD बनाइए जिसमें BC = 7.5 सेमी, AC = AD = 6 सेमी, CD = 5 सेमी और BD = 10 सेमी। चौथी भुजा की माप नापकर ज्ञात कीजिए।
उत्तर

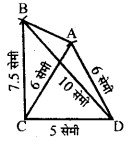
रचना :

1. सर्वप्रथम रेखाखंड CD = 5.0 सेमी खचा।।
2. फिर C तथा D को केन्द्र मानकर 6 सेमी की त्रिज्या के दो चाप खींचे जो एक-दूसरे को बिन्दु A पर काटते हैं।
3. D को केन्द्र मानकर 10 सेमी की त्रिज्या का एक तथा C को केन्द्र मानकर 75 सेमी त्रिज्या का दूसरा चाप खींचा जो पहले चाप को बिन्दु B पर काटता है ।
4. AB, BD तथा CB को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है। नापने पर, AB = 4.8 सेंमी०

प्रश्न 3.
एक समान्तर चतुर्भुज बनाइए, जिससे एक भुजा 4.4 सेमी तथा दोनों विकर्ण क्रमशः 5.6 सेमी और 7.0 सेमी हो। दूसरी भुजा की माप ज्ञात कीजिए।
[संकेत- समांतर चतुर्भज के विकर्ण एक दूसरे को समविभाजित करते हैं।]
उत्तर
रचना :

1. सर्वप्रथम रेखाखंड AB = 4.4 सेमी खींचा।।
2. फिर A को केन्द्र मानकर 2.8 सेमी तथा 3.5 सेमी त्रिज्या के दो चाप लगाए जो एक-दूसरे को बिन्दु 0 पर काटते हैं।
3. BO को BD = 7.0 सेमी तथा AO को AC=5.6 सेमी तक आगे बढ़ाया।
4. DA, BC तथा CD को मिलाया।

अतः ABCD अभीष्ट समान्तर चतुर्भुज है। दूसरी भुजा की माप = 4.8 सेमी

प्रश्न 4.
एक चतुर्भुज ABCD बनाइए जिसमें AB = 3.0 सेमी, CD = 3.0 सेमी, DA= 7.5 सेमी, AC = 8.0 सेमी और BD = 5.5 सेमी।।
उत्तर
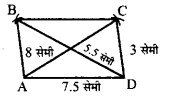
रचना :

1. सर्वप्रथम रेखाखंड AD = 7.5 सेमी खींचा।
2. फिर बिन्दु A को केन्द्र मानकर 8 सेमी एवं बिन्दु D को केन्द्र मानकर 3 सेमी के चाप लगाए, जो एक-दूसरे को बिन्दु C पर काटते हैं।
3. AC एवं CD को मिलाया।
4. पुनः बिन्दु A को केन्द्र मानकर 3 सेमी एवं. बिन्दु D को केन्द्र मानकर 5.5 सेमी के चाप लगाए, जो एक-दूसरे को बिन्दु B पर काटते हैं।
5. अब AB, BD एवं BC को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है ।

प्रश्न 5.
एक वर्ग बनाइए जिसका विकर्ण 6.4 सेमी हो।
[संकेत – वर्ग के विकर्ण एक दूसरे को समकोण पर समविभाजित करते हैं।]
उत्तर
रचना :

1. सर्वप्रथम AC = 6.4 सेमी का रेखाखंड खींचा।
2. फिर AC का लम्बार्द्धक खींचा जो AC को 0 पर काटता है।
3. बिन्दु 0 से विकर्ण का आधा 64 = 3.2 सेमी के चाप दोनों ओर लगाए जो लम्बार्द्धक को क्रमशः बिन्दु B तथा D पर काटते हैं ।
4. AB, BC, CD तथा DA को मिलाया ।

अतः ABCD अभीष्ट वर्ग है ।।

अभ्यास 10 (d)

प्रश्न 1.
चतुर्भुज ABCD बनाइए जिसमें AB = 5.5 सेमी, BC = 3.7 सेमी, ∠A = 60°, ∠B = 105° और ∠D = 90°।।
उत्तर
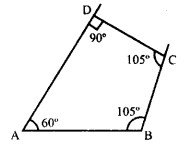
रचना :
∠C = 360° – (60° + 105° + 90°) = 105°

1. सर्वप्रथम रेखाखंड AB = 5.5 सेमी खचा।
2. फिर AB के बिन्दु A तथा B से क्रमशः 60° तथा 105° के कोण बनाए।
3. बिन्दु B से 3.7 सेमी० की त्रिज्या का चाप लगाकर BC काटा।
4. बिन्दु C से 105 का कोण बनाया जो 60° के कोण को बिन्दु D पर काटता है।

अतः ABCD अभीष्ट चतुर्भुज है।

प्रश्न 2.
एक आयत की रचना कीजिये जिसकी भुजायें 4.5 सेमी और 6.0 सेमी हो। इसके दोनों विकण को नापिए।
उत्तर
रचना :

1. सर्वप्रथम रेखाखंड AB = 6 सेमी खींचा।
2. फिर बिन्दु A तथा B पर 90° का कोण बनाया ।
3. बिन्दु A तथा B को केन्द्र मानकर 4.5 सेमी की त्रिज्या से 5 चाप लगाये जो क्रमशः D तथा C हैं ।
4. बिन्दु C तथा D को मिलाया ।

अतः ABCD अभीष्ट आयत है ।
नापने पर, विकर्ण BD = 7.5 सेमी

प्रश्न 3.
चतुर्भुज PQRS की रचना कीजिए, जिसमें PQ = 3.5 सेमी, QR = 6.5 सेमी, ∠P=∠R = 105° और ∠S = 75°।
[संकेत – ∠Q= 360°- (105° +105° + 75°) = 75°]
उत्तर
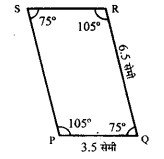
रचना :
∠Q= 360° – (105° + 105° + 75°) = 75°

1. सर्वप्रथम रेखाखंड PQ= 3.5 सेमी खींचा।
2. PQ के बिन्दु P तथा Q से क्रमशः 105° तथा 75° के कोण बनाए।
3. फिर Q को कोण मानकर 6.5 सेमी का चाप लगाया।
4. बिन्दु R से 105° का कोण बनाया जो कोण P को बिन्दु S पर काटता है।

अतः PQRS अभीष्ट चतुर्भुज है ।

प्रश्न 4.
एक चतुर्भुज ABCD बनाइए जबकि BC = 5.5 सेमी, CD = 4.1 सेमी, ∠A = 70°, ∠B = 110 और ∠D= 85°। AB और DA को नापिए।
उत्तर
रचना :
∠C = 360° – (70° + 110° + 85°) = 95°

1. सर्वप्रथम रेखाखंड BC = 5.5 सेमी खींचा।
2. फिर BC के बिन्दु B तथा C से क्रमशः 110° तथा 95° के कोण बनाये।
3. बिन्दु C से 4.1 सेमी का एक चाप खींचा जो ∠C को बिन्दु D पर काटता है।
4. बिन्दु D से 85° का कोण बनाया जो 110° का कोण बनाने वाली रेखा को बिन्दु A पर काटता है।

अतः ABCD अभीष्ट चतुर्भुज है।
नापने पर, AB = 4.5 सेमी और DA= 6.6 सेमी

अभ्यास 10 (e)

प्रश्न 1.
एक चतुर्भुज ABCD बनाइए, जबकि AB = 4.2 सेमी, BC = 3.6 सेमी, CD = 4.8 सेमी, ∠B = 30° और ∠C = 150°। भुजा AD मापिए।
उत्तर
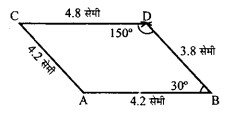
रचना :

1. सर्वप्रथम रेखाखंड AB = 4.2 सेमी खींचा। 4.8 सेमी ।
2. फिर AB के बिन्दु B से 30° का कोण बनाया।
3. बिन्दु B से 3.6 सेमी की त्रिज्या का एक चाप लगाया जो । 30° के कोण को बिन्दु C पर काटता है।
4. बिन्दु C से 150° का कोण बनाकर 4.8 सेमी की त्रिज्या का चाप लगाया जो 150° के कोण को बिन्दु D पर काटता है।
5. DA को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है। नापने पर, भुजा AD = 4.2 सेमी

प्रश्न 2.
चतुर्भुज PQRS बनाइए, जिसमें PQ= 3.5 सेमी, QR = 2.5 सेमी, RS = 4.1 सेमी, ∠Q= 75°, ∠R = 120°। भुजा PS मापिए।
उत्तर
रचना :

1. सर्वप्रथम रेखाखंड PQ= 3.5 सेमी खींचा।
2. PQ के बिन्दु Q से 75° का कोण बनाया तथा 2.5 सेमी त्रिज्या का एक चाप र्वीचा जो 75° के कोण को बिन्दु R पर काटता है ।
3. बिन्दु R से 120° का कोण बनाकर 4.1 सेमी की त्रिज्या का चाप खींचा जो 120° के कोण को बिन्दु S पर काटता है।
4. SP को मिलाया।

अतः PQRS अभीष्ट चतुर्भुज है। नापने पर भुजा SP= 3.4 सेमी।

प्रश्न 3.
चतुर्भुज ABCD बनाइये जिसमें AB = BC = 3 सेमी, AD = 5 सेमी, ∠A = 90°, ∠B = 105°।
उत्तर
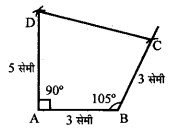
रचना :

1. सर्वप्रथम रेखाखंड AB = 3 सेमी खींचा।
2. फिर AB के बिन्दु B से 105° का कोण बनाया तथा 3 सेमी की त्रिज्या को चोप लगाया जो 105° के कोण को बिन्दु C पर काटता है |
3. AB के बिन्दु A से 90° का कोण बनाया तथा 5 सेमी की 9 105/ त्रिज्या का चाप लगाया जो 90° के कोण को बिन्दु D पर काटता है।
4. CD को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है।

प्रश्न 4.
एक चतुर्भुज PQRS की रचना कीजिए जिसमें ∠Q=135°, ∠R = 90°, ∠R = 5.0 सेमी, PQ=9 सेमी और RS = 7 सेमी।
उत्तर
रचना :

1. सर्वप्रथम रेखाखंड QR = 5 सेमी खींचा।
2. फिर QR के बिन्दु Q तथा R से क्रमशः 45° तथा 90° के कोण बनाए।
3. बिन्दु R पर 7 सेमी की त्रिज्या का चाप खींचा जो ∠R को S पर काटता है।
4. बिन्दु Qपर 9 सेमी की त्रिज्या का चाप खींचा जो ∠Q को P पर काटता है।
5. PS को मिलाया।

अतः PQRS अभीष्ट चतुर्भुज है।

अभ्यास 10 (f)

प्रश्न 1.
चतुर्भुज ABCD की रचना कीजिए, जिसमें AB = BC = 3 सेमी, AD = CD =5 सेमी. तथा ∠ABC = 1200 हो।
उत्तर
रचना :

1. सर्वप्रथम रेखाखंड AB = 3 सेमी खींचा ।
2. फिर बिन्दु B पर 120° का कोण बनाया तथा BC = 3 सेमी त्रिज्या का चाप लगाया।
3. फिर C को केन्द्र मानकर 5 सेमी त्रिज्या का चाप लगाया।
4. A को केन्द्र मानकर 5 सेमी त्रिज्या का चाप लगाया जो पहले चाप को बिन्दु D पर काटता है।
5. CD,DA को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है।

प्रश्न 2.
चतुर्भुज ABCD की रचना कीजिए, जिसमें AB= 2.8 सेमी, BC=3.1 सेमी, CD=2.6 सेमी, DA = 3.3 सेमी और ∠A = 60° हो।
उत्तर
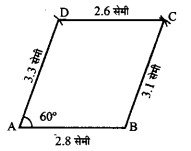
रचना :

1. सर्वप्रथम रेखाखंड AB = 2.8 सेमी खींचा।
2. फिर AB के बिन्दु A पर 60° का कोण बनाया तथा 3.3 सेमी का चाप लगाया जो ∠A को बिन्दु D पर काटता है।
3. बिन्दु B से 3.1 सेमी का तथा बिन्दु D से 2.6 सेमी को चाप लगाया जो एक-दूसरे को बिन्दु C पर काटते हैं।
4. BC, CD को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है । विकर्ण AC = 4.8 सेमी०

प्रश्न 3.
एक आयत की रचना कीजिए, जिसकी भुजाएँ 4.2 सेमी० और 2.5 सेमी० हो। इसके विकर्ण की लम्बाई नापिए।
उत्तर
रचना :

1. सर्वप्रथम रेखाखंड AB = 4.2 सेमी खींचा।
2. बिन्दु A तथा B प्रत्येक पर 90° का कोण बनाए।
3. बिन्दु A तथा B को केन्द्र मानकर 2.5 सेमी त्रिज्या से चाप लगाए जो क्रमशः बिन्दु D तथा C हैं।
4. CD को मिलाया।

अतः ABCD अभीष्ट आयत है। विकर्ण AC = 4.8 सेमी०

प्रश्न 4.
एक समचतुर्भुज की रचना कीजिए जिसमें एक कोण 75° तथा एक भुजा 5.2 सेमी हो।
उत्तर
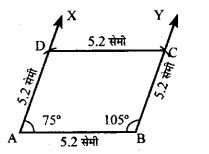
रचना :

1. सर्वप्रथम रेखाखंड AB = 5.2 सेमी खींचा।
2. फिर बिन्दु A से 75° का कोण बनाती हुई रेखा खींची तथा AD = 5.2 सेमी काटा।
3. फिर बिन्दु B तथा D को केन्द्र मानकर 5.2 सेमी त्रिज्या के चाप लगाए जो एक-दूसरे को बिन्दु C पर कांटते हैं।
4. BC तथा DC को मिलाया।

अतः ABCD अभीष्ट समचतुर्भुज है।

प्रश्न 5.
एक वर्ग बनाइए, जिसकी एक भुजा 5.0 सेमी० हो।
उत्तर

रचना :

1. सर्वप्रथम रेखाखंड AB = 5 सेमी खींचा।
2. फिर बिन्दु A तथा B से क्रमशः 90° के कोण बनाती हुई रेखा है* खींची।
3. बिंदु A तथा B से 5 सेमी त्रिज्या लेकर चाप लगाए जो ∠A तथा ∠B को क्रमशः बिन्दु D तथा C काटते हैं।
4. c तथा D को मिलाया।

अतः ABCD अभीष्ट वर्ग है।

दक्षता अभ्यास – 10

प्रश्न 1.
निम्नांकित नाप से चतुर्भुज ABCD की रचना कीजिए।
(i) AB = 2.5 सेमी, BC = 7.5 सेमी CD = 10 सेमी, DA= 7.5 सेमी, BD = 6.5 सेमी।
उत्तर

रचना :

1. सर्वप्रथम रेखाखंड CD = 10 सेमी खींचा।
2. फिर बिन्दु C तथा D को केन्द्र मानकर क्रमशः 7.5 सेमी तथा 6.5 सेमी की त्रिज्या के चाप लगाए जो एक-दूसरे को बिन्दु B पर काटते हैं।
3. फिर बिन्दु B को केन्द्र मानकर 2.5 सेमी त्रिज्या का तथा पुनः बिन्दु D को केन्द्र मानकर 7.5 सेमी त्रिज्या का एक चाप लगाया जो एक-दूसरे को बिन्दु A पर काटते हैं।
4. DA, AB, BC, तथा BD को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है।

(ii) AB = 4 सेमी, BC = 3 सेमी, CD = 6 सेमी, ∠B = 135°, ∠C = 60°।
उत्तर

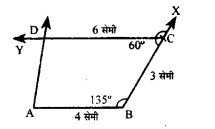
रचना :

1. सर्वप्रथम रेखाखंड AB = 4 सेमी खींचा।
2. AB के बिन्दु B से 135°का कोण बनाते हुए BC = 3 सेमी । का चाप काटा।
3. C पर 60° का कोण बनाते हुए CD= 6 सेमी का चाप काटा।
4. AD को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है।

(iii) BC = 4 सेमी, ∠C = 120°, CD =5 सेमी, ∠BDA = 26°, ∠A= 64°।
उत्तर

रचना : ∠B = 360° – (120° +26° + 64°) = 150°

1. सर्वप्रथम रेखाखंड BC = 4 सेमी खींचा।
2. BC के बिन्दु C पर 120° का कोण बनाया।
3. बिन्दु C को केन्द्र मानकर 5 सेमी का चाप खींचा जो ∠C को बिन्दु A पर काटता है।
4. BD को मिलाया।
5. बिन्दु D पर ∠BDA = 26° बनाया।
6.  बिन्दु B पर 150° का कोण बनाया जो ∠BDA को बिन्दु A पर काटता है।
7. AD, BA को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है।

प्रश्न 2.
एक वर्ग ABCD की रचना कीजिए, जिसकी भुजा 4 सेमी हो।AC को नापिए।
उत्तर

रचना :

1. सर्वप्रथम रेखाखंड AB = 4 सेमी खचा ।
2. फिर बिन्दु A तथा B पर 90° का कोण बनाया।
3. बिन्दु A तथा C से 4 सेमी की त्रिज्या लेकर चाप लगाये | जो 90° के कोणों को क्रमशः D तथा C बिन्दु पर काटते हैं ।
4. CD तथा AC को मिलाया ।

अतः ABCD अभीष्ट वर्ग है । नापने पर, विकर्ण AC = 5.6 सेमी 3 4 सेमी B

प्रश्न 3.
एक आयत ABCD बनाइए जब कि AB = 4 सेमी और AC = 6 सेमी हो।AD को नापिए।
उत्तर

रचना :

1. सर्वप्रथम रेखाखंड AB = 4 सेमी खींचा।
2. बिन्दु A तथा B पर 90° का कोण बनाया।
3. बिन्दु A को केन्द्र मानकर 6 सेमी त्रिज्या का चाप लगाया जो ∠B को बिन्दु C पर काटता है।
4. बिन्दु C पर 90° का कोण बनाया जो ∠A को बिन्दु D पर काटता है ,

अतः ABCD अभीष्ट आयत है । नापने पर, भुजा AD = 4.5 सेमी

प्रश्न 4.
समांतर चतुर्भुज ABCD की रचना कीजिए जिसकी भुजायें 5.8 सेमी, 6.2 सेमी तथा विकर्ण 7.3 सेमी हों। इसका दूसरा विकर्ण मापकर लिखिए।
उत्तर

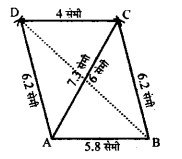
रचना :

1. सर्वप्रथम रेखाखंड AB = 5.8 सेमी खचा।
2. बिन्दु A से 7.3 सेमी तथा B से 6.2 सेमी की त्रिज्या के | चाप लगाए जो एक-दूसरे को बिन्दु C पर काटते है।
3. अब C से 5.8 सेमी तथा A से 6.2 सेमी की त्रिज्या के चाप लगाए जो एक-दूसरे को बिन्दु D पर काटते हैं।
4. AC, BC, AD तथा DC को मिलाया।

अतः ABCD अभीष्ट समान्तर चतुर्भुज है। नापने पर, विकर्ण BD = 9.4 सेमी

प्रश्न 5.
एक आयत ABCD बनाइए जबकि AB = 5 सेमी, AC = 6 सेमी। ∠BAD मापिए।
उत्तर

रचना :

1. सर्वप्रथम रेखाखंड AB =5 सेमी खींचा।
2. फिर बिदु A तथा B पर 90° का कोण बनाया।
3. बिन्दु A से 6 सेमी की त्रिज्या का चाप लगाया जो बिन्दु B पर 90° के कोण को बिन्दु C पर काटता है।
4. बिन्दु C को केन्द्र मानकर 5 सेमी की त्रिज्या का चाप लगाया जो बिन्दु A पर 90° के कोण को बिन्दु D पर काटता है।
5. AC तथा CD को मिलाया।

अतः ABCD अभीष्ट आयत है। नापने पर, ∠BAD = 90°

प्रश्न 6.
एक-चतुर्भुज ABCD बनाइए, जिसमें AB = 4.1 सेमी, BC = 4.5 सेमी, CD = 3 सेमी, AD = 3.7 सेमी तथा विकर्ण AC = 4.2 सेमी।।
उत्तर

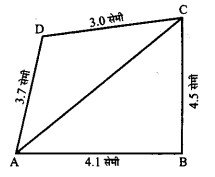
रचना :

1. सर्वप्रथम रेखाखंड AB = 4.1 सेमी खींचा।
2. फिर बिन्दु A को केन्द्र मानकर 4.2 सेमी त्रिज्या का एक चाप खींचा।
3. विन्दु B को केन्द्र मानकर 4.5 सेमी त्रिज्या का दूसरा चाप खचा जो पहले चाप को बिन्दु C पर काटता है।
4. फिर A को केन्द्र मानकर 3.7 सेमी तथा C को केन्द्र मानकर 3 सेमी की त्रिज्या के चाप लगाएँ जो एक-दूसरे को बिन्दु D पर। काटते हैं।
5. AC, BC, AD तथा CD को मिलाया।

अतः ABCD अभीष्ट चतुर्भुज है ।

प्रश्न 7.
एक समबहुभुज के अन्तःकोण की माप 108° है तो उसके भुजाओं की संख्या होगी।
उत्तर
भुजाओं की संख्या = 5 (क्योंकि पंचभुज के अन्तःकोणों का योग = 540° होता है।)

We hope the UP Board Solutions for Class 8 Maths Chapter 10 चतुर्भुज की रचनाएँ help you.