UP Board Solutions for Class 8 Maths Chapter 9 समान्तर रेखाएँ
UP Board Solutions for Class 8 Maths Chapter 9 समान्तर रेखाएँ
समान्तर रेखाएँ
अभ्यास 9 (a)
प्रश्न 1.
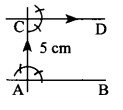
दी हुई रेखा AB से 5 सेमी० की दूरी पर AB के समान्तर एक रेखा खींचिए।
उत्तर
दी हुई रेखा AB के बिन्दु A पर लम्ब खींचते हैं जिसमें से AC=5 सेमी० काटते हैं। बिन्दु C पर लम्ब रेखा खींचते हैं। यह रेखा CD अभीष्ट रेखा है जिसकी रेखा AB से दूरी 5 सेमी है।
प्रश्न 2.
किसी दी हुई रेखा के बाहर स्थित बिन्दु से होकर जानी वाली एक समांतर रेखा खींचिए।
उत्तर
रचना : दी हुई रेखा AB के बाहर स्थित कोई
बिन्दु P है। पटरी व परकार की सहायता से।
बिन्दु P से AB के समान्तर रेखा CD खींची ।
प्रश्न 3.
पार्श्व चित्र में त्रिभुज ABC के आधार BC के समान्तर DE और FG रेखाखंड खीचें गए हैं कि निम्नलिखित के उत्तर दीजिए।
(i) कितने समलम्ब हैं?
(ii) कितने त्रिभुज हैं?
उत्तर

- तीन समलम्ब FGED, FGCB तथा DECB हैं ।
- तीन त्रिभुज ABC, ADE, तथा AFG हैं ।
प्रश्न 4.
पार्श्व चित्र में । और m दो समान्तर सरल रेखाएँ तथा t एक तिर्यक रेखा है। यदि ∠1 = 30°, शेष कोणों 2,3,4,5,6,7 और 8 के मान ज्ञात कीजिए।
उत्तर
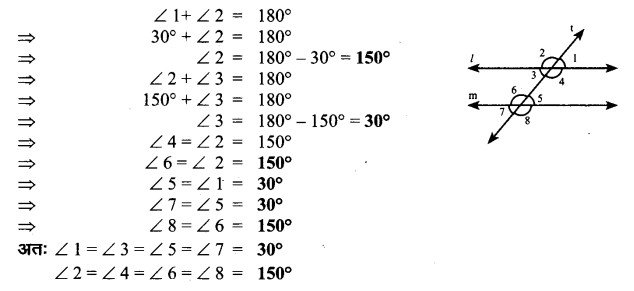
प्रश्न 5.
पाश्र्व चित्र में ABC एक त्रिभुज है तथा BD भुजा AC के समान्तर है, ∠ACB = 30° तथा ∠ABD = 28°, ∠ABC, ∠DBK और ∠BAC के मान ज्ञात कीजिए।
उत्तर

प्रश्न 6.
पार्श्व चित्र में r ⊥ p और r ⊥ q
(i) क्या p॥q? क्यों?
(ii) यदि p॥q तथा ∠1 = 63° हो, तो ∠2 का मान ज्ञात कीजिए।
उत्तर

- p॥q क्योंकि एक ही रेखा पर दो लम्ब रेखाएँ परस्पर समान्तर होती है।
- यदि दो समान्तर रेखाओं को एक त्रिर्यक रेखा काटे तो संगत कोण बराबर होते है।
∵ ∠1=63°
∴ ∠2= 63°
अभ्यास 9 (b)
प्रश्न 1.
चतर्भज ABCD का प्रत्येक कोण समकोण है। सत्यापित कीजिए कि AB || DC और AD || BC,
उत्तर

प्रश्न 2.
पाश्र्व चित्र में दो रेखाएँ । और m हैं जिसे एक तिर्यक रेखा T बिन्दुओं P और Q काटती हैं। यदि ∠2 = ∠3 = ∠90 सत्यापित कीजिए कि रेखाएँ l और m परस्पर समान्तर हैं। ∠1 + ∠3 का मान कितना होगा?
उत्तर

प्रश्न 3.
ABCD एक समलम्ब चतुर्भुज है जिसमें AD || BC है। रेखाखंड BL और CM रेखा AD पर लम्ब हैं दिखाइए BL || CM | यदि BC = ML हो तो दिखाइए कि BCML एक वर्ग है।
उत्तर

प्रश्न 4.
ABCD एक वर्ग है तथा L, M, N और O क्रमशः भुजाओं AB, BC, CD तथा DA के मध्य बिन्दु हैं। कोण तथा भुजाएँ नापकर देखिए कि आकृति LMNO भी एक वर्ग है।
उत्तर

प्रश्न 5.
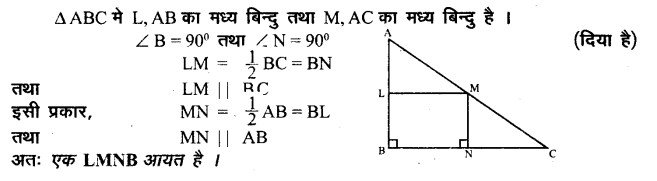
त्रिभुज ABC में कोण B एक समकोण है। L और M क्रमशः भुजाओं AB और AC के मध्य बिन्दु हैं। MN भुजा BC पर लम्ब है। दिखाइए कि आकृति LMNB एक आयत है।
उत्तर
प्रश्न 6.
पार्श्व चित्र में 1|| m, p ⊥ m और p ⊥ n
(i) क्या? m || n? क्यों?
(ii) क्या? l || n? क्यों?
(iii) क्या? p ⊥ l? क्यों?
उत्तर

- हाँ, क्योंकि संगत कोण बराबर हैं।
- हाँ, क्योंकि L|| M और M || N|
∴ L|| N - हाँ, क्योंकि P, MN पर ⊥ है और L भी समान्तर है।
अभ्यास 9 (c)
प्रश्न 1.
10 सेमी० का एक रेखाखंड AB खींच कर इसको पाँच बराबर भागों में पटरी परकार की सहायता से विभक्त कीजिए। मापकर प्रत्येक भाग की लम्बाई जाँचिए।
उत्तर
रचना :
- सर्वप्रथम रेखाखंड AB = 10 सेमी ची।।
- रेखाखंड के अन्त्य बिन्दु A से न्यूनकोण बनाती हुई एक किरण AL खींची ।
- किसी त्रिज्या से किरण AL पर पाँच बराबर भाग AM1, M1M2, M2M3, M4M5 तथा M4M5 किए।
- बिन्दु M5 को B से मिलाया।
- M4, M3 M2 तथा M1 से BM5 के समान्तर रेखायें खींची जो रेखाखंड AB को क्रमशः CD, E और F बिन्दु पर काटते हैं।
इस प्रकार बिन्दु C, D, E और F रेखाखंड AB को पाँच बराबर खंडों में विभक्त करते हैं। नापने पर, प्रत्येक भाग की लम्बाई = 2 सेमी०
प्रश्न 2.
एक 8 सेमी लम्बी रेखाखंड को 2:3 अनुपात में विभक्त कीजिए। इस प्रकार प्राप्त दोनों भाग की लम्बाई मापकर सत्यापित कीजिए कि इनका अनुपात 2:3 है।
उत्तर

रचना :
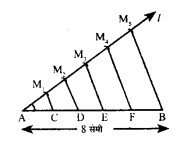
- सर्वप्रथम रेखाखंड AB = 8 सेमी खींची।
- रेखाखंड AB के बिन्दु A से न्यूनकोण बनाती हुई किरण AM खींची।
- आनुपातिक अंक 2 और 3 के योग 5 के बराबर किरण AM में A से प्रारंभ करके किसी त्रिज्या से पाँच समान रेखाखंड AM1, M1M2, M2M3, M3M4 तथा M4M5, चिहनित किया।
- फिर अन्तिम चिहनित बिन्दु को रेखाखंड के अन्त्य बिन्दु B से मिलाया।
- M5B के समान्तर M2 से एक रेखाखंड M2P खींचा जो रेखाखंड AB को P काटता है। इस प्रकार बिन्दु P रेखाखंड AB को 2:3 में विभक्त करता है।
सत्यापन – AP और PB को मापा। मापने पर,
अतः उत्तर सही है।
प्रश्न 3.
8 सेमी माप का रेखाखंड AB खींचिए। अन्त्य बिन्दु A से इस रेखाखंड का वाँ भाग रचना द्वारा ज्ञात कीजिए।
उत्तर

रचना :
- सर्वप्रथम रेखाखंड AB = 8 सेमी खींची ।।
- फिर रेखाखंड AB के बिन्दु A से न्यूनकोण बनाती हुई किरण AM खींची।
- इसके बाद AM में बिन्दु A से किसी त्रिज्या से पाँच समान रेखाखंड M1, M2, M3 M4 तथा M5 चिहनित किए।
- फिर अन्तिम चिहनित बिन्दु M5 को रेखाखंड के अन्त्य बिन्दु B से मिलाया।
- अन्त में M5B के समान्तर M3 से एक रेखाखंड M3P खींचा, जो रेखाखंड AB को बिन्दु P पर काटता है ।
इस प्रकार, बिन्दु P रेखाखंड AB को वे भाग में विभक्त करता है।
प्रश्न 4.
8.4 सेमी० का एक रेखाखंड AB खींचिए। इस पर एक बिन्दु P रचना द्वारा इस प्रकार ज्ञात कीजिए कि ।
उत्तर

रचना :
- सर्वप्रथम रेखाखंड AB = 8.4 सेमी० खींची।
- फिर रेखाखंड AB के अन्त्य बिन्दु A से न्यूनकोण बनाती हुई किरण AM खींची।
- इसके बाद AM में बिन्दु A से किसी त्रिज्या के पाँच समान M1, M2, M3, M4 तथा M5 चिहनित किए।
- फिर अन्तिम चिहनित बिन्दु M5 को रेखाखंड के अन्त्य बिन्दु B से मिलाया।
- अन्त में M5B के समान्तर M2 से एक रेखाखंड M2P खींचा, जो रेखाखंड AB को । बिन्दु P पर काटता है।
इस प्रकार, बिन्दु P रेखाखंड AB को वें भाग में विभक्त करता है।
We hope the UP Board Solutions for Class 8 Maths Chapter 9 समान्तर रेखाएँ help you.