UP Board Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments (किरण प्रकाशिकी एवं प्रकाशिक यंत्र)
UP Board Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments (किरण प्रकाशिकी एवं प्रकाशिक यंत्र)
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर
प्रश्न 1.
2.5 cm साइज़ की कोई छोटी मोमबत्ती 36 cm वक्रता त्रिज्या के किसी अवतल दर्पण से 27 cm दूरी पर रखी है। दर्पण से किसी परदे को कितनी दूरी पर रखा जाए कि उसका सुस्पष्ट प्रतिबिम्ब परदे पर बने। प्रतिबिम्ब की प्रकृति और साइज़ का वर्णन कीजिए। यदि मोमबत्ती को दर्पण की ओर ले जाएँ, तो परदे को किस ओर हटाना पड़ेगा?
हल-
दिया है, u = -27 सेमी, O = 2.5 सेमी

अत: प्रतिबिम्ब वास्तविक, उल्टा तथा 5 सेमी ऊँचा है। यदि मोमबत्ती को पर्दे की ओर ले जायें, तो पर्दे को दर्पण से दूर ले जाना होगा। यदि मोमबत्ती को 18 सेमी से कम दूरी तक खिसकायें, तो प्रतिबिम्ब आभासी बनेगा तथा पर्दे पर प्राप्त नहीं होगा।
प्रश्न 2.
4.5 cm साइज़ की कोई सुई 15 cm फोकस दूरी के किसी उत्तल दर्पण से 12 cm दूर रखी है। प्रतिबिम्ब की स्थिति तथा आवर्धन लिखिए। क्या होता है जब सुई को दर्पण से दूर ले जाते हैं? वर्णन कीजिए।
हल-
यहाँ सुई का आकार O = 4.5 सेमी; उत्तल दर्पण की फोकस दूरी f = 15 सेमी। दर्पण से वस्तु (सुई) की दूरी u = -12 सेमी

अर्थात् प्रतिबिम्ब सीधा (आभासी) तथा 2.5 सेमी लम्बा (ऊँचा) बनेगा।
जब सुई को दर्पण से दूर ले जाते हैं तो इसका प्रतिबिम्ब दर्पण से दूर फोकस की ओर खिसकेगा तथा इसका आकार घटता जायेगा।
प्रश्न 3.
कोई टैंक 12.5 cm ऊँचाई तक जल से भरा है। किसी सूक्ष्मदर्शी द्वारा बीकर की तली पर पड़ी किसी सुई की आभासी गहराई 9.4 cm मापी जाती है। जल का अपवर्तनांक क्या है? बीकर में उसी ऊँचाई तक जल के स्थान पर किसी 1.63 अपवर्तनांक के अन्य द्रव से प्रतिस्थापन करने पर सुई को पुनः फोकसित करने के लिए सूक्ष्मदर्शी को कितना ऊपर/नीचे ले जाना होगा?
हल-
सुई की वास्तविक गहराई h = 12.5 सेमी
आभासी गहराई h’ = 9.4 सेमी

पहले सूक्ष्मदर्शी 9.4 सेमी पर फोकस था अतः इसका नीचे की ओर विस्थापन = (9.4 – 1.7) सेमी = 1.7 सेमी
प्रश्न 4.
चित्र 9.1 (a) तथा (b) में किसी आपतित किरण का अपवर्तन दर्शाया गया है जो वायु में क्रमशः काँच-वायु तथा जल-वायु अन्तरापृष्ठ के अभिलम्ब से 60° का कोण बनाती है। उस आपतित किरण का अपवर्तन कोण ज्ञात कीजिए, जो जल में जल-काँच अन्तरापृष्ठ के अभिलम्ब से 45° का कोण बनाती है [चित्र 9.1(c)]
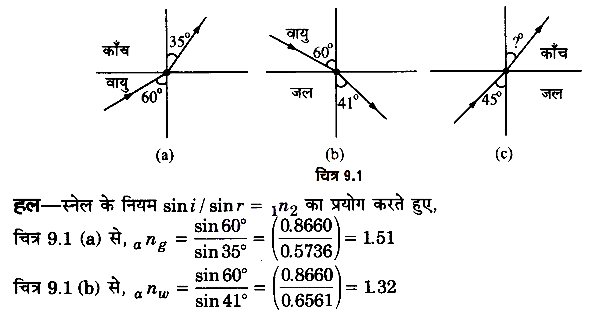

प्रश्न 5.
जल से भरे 80 cm गहराई के किसी टैंक की तली पर कोई छोटा बल्ब रखा गया है। जल के पृष्ठ का वह क्षेत्र ज्ञात कीजिए जिससे बल्ब का प्रकाश निर्गत हो सकता है। जल का अपवर्तनांक 1.33 है। (बल्ब को बिन्दु प्रकाश स्रोत मानिए)
हल-
टैंक की तली में रखे बल्ब से निकलने वाली प्रकाश किरणें जल के पृष्ठ से तभी निर्गत होंगी, जबकि आपतन कोण जल-वायु अन्तरापृष्ठ के लिए क्रान्तिक कोण C से कम अथवा उसके बराबर हो। यदि उसे पृष्ठ के क्षेत्रफल की त्रिज्या हो जिससे बल्ब का प्रकाश निकल रहा है, तो यह स्थिति चित्र 9.2 की भाँति होगी जहाँ h बल्ब की जल के तल से गहराई है।
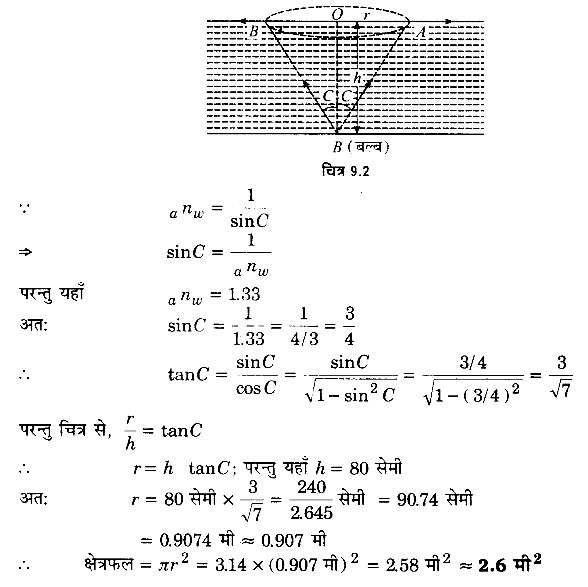
प्रश्न 6.
कोई प्रिज्म अज्ञात अपवर्तनांक के काँच का बना है। कोई समान्तर प्रकाश-पुंज इस प्रिज्म के किसी फलक पर आपतित होता है। प्रिज्म का न्यूनतम विचलन कोण 40° मापा गया। प्रिज्म के पदार्थ का अपवर्तनांक क्या है? प्रिज्म का अपवर्तन कोण 60° है। यदि प्रिज्म को जल (अपवर्तनांक 1.33) में रख दिया जाए तो प्रकाश के समान्तर पुंज के लिए नए न्यूनतम विचलन कोण का परिकलन कीजिए।
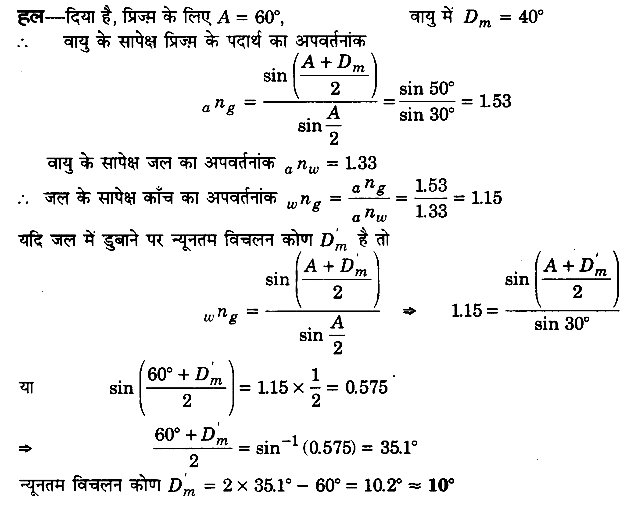
प्रश्न 7.
अपवर्तनांक 1.55 के काँच से दोनों फलकों की समान वक्रता त्रिज्या के उभयोत्तल लेन्स निर्मित करने हैं। यदि 20 cm फोकस दूरी के लेन्स निर्मित करने हैं तो अपेक्षित वक्रता त्रिज्या क्या होगी?

प्रश्न 8.
कोई प्रकाश-पुंज किसी बिन्दु P पर अभिसरित होता है। कोई लेन्स इस अभिसारी पुंज के पथ में बिन्दु P से 12 cm दूर रखा जाता है। यदि यह
(a) 20 cm फोकस दूरी का उत्तल लेन्स है,
(b) 16 cm फोकस दूरी का अवतल लेन्स है तो प्रकाश-पुंज किस बिन्दु पर अभिसरित होगा?
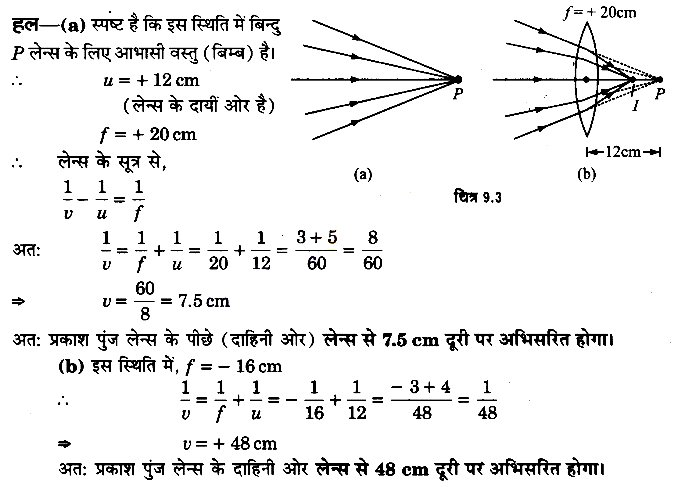
प्रश्न 9.
3.0 cm ऊँची कोई बिम्ब 21 cm फोकस दूरी के अवतल लेन्स के सामने 14 cm दूरी पर रखी है। लेन्स द्वारा निर्मित प्रतिबिम्ब का वर्णन कीजिए। क्या होता है जब बिम्ब लेन्स से दूर हटती जाती है?
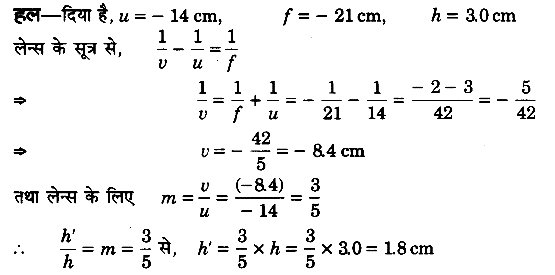
अतः प्रतिबिम्ब 1.8 cm लम्बा आभासी तथा सीधा होगा, जो लेन्स के बायीं ओर उससे 8.4 cm की दूरी पर बनेगा। जैसे-जैसे बिम्ब लेन्स से दूर हटती है, (u → ∞) वैसे-वैसे प्रतिबिम्ब फोकस के समीप खिसकता जाता है (v → f)।
प्रश्न 10.
किसी 30 cm फोकस दूरी के उत्तल लेन्स के सम्पर्क में रखे 20 cm फोकस दूरी के अवतल लेन्स के संयोजन से बने संयुक्त लेन्स (निकाय) की फोकस दूरी क्या है? यह तन्त्र अभिसारी लेन्स है अथवा अपसारी? लेन्सों की मोटाई की उपेक्षा कीजिए।

प्रश्न 11.
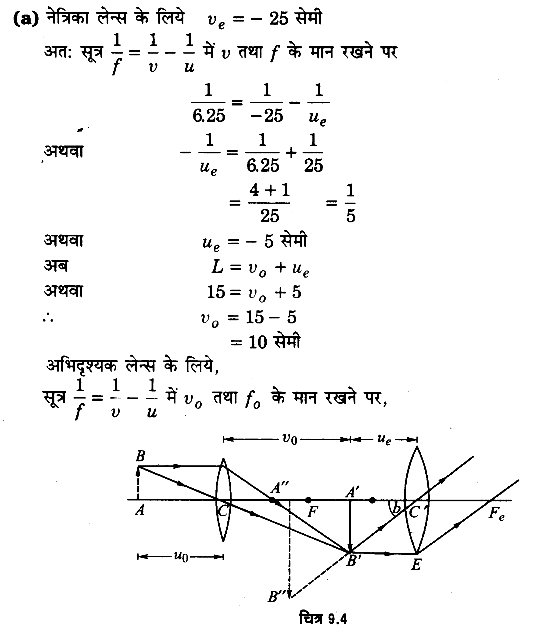
किसी संयुक्त सूक्ष्मदर्शी में 2.0 cm फोकस दूरी का अभिदृश्यक लेन्स तथा 6.25 cm फोकस दूरी का नेत्रिका लेन्स एक-दूसरे से 15 cm दूरी पर लगे हैं। किसी बिम्ब को अभिदृश्यक से कितनी दूरी पर रखा जाए कि अन्तिम प्रतिबिम्ब
(a) स्पष्ट दृष्टि की अल्पतम दूरी (25 cm), तथा
(b) अनन्त पर बने? दोनों स्थितियों में सूक्ष्मदर्शी की आवर्धन क्षमता ज्ञात कीजिए।
हल-
दिया है, अभिदृश्यक लेन्स की फोकस दूरी fe = 2.0 सेमी
नेत्रिका लेन्स की फोकस दूरी f0 = 6.25 सेमी।
दोनों लेन्सों के बीच की दूरी L = 15 सेमी
स्पष्ट दृष्टि की अल्पतम दूरी D = 25 सेमी


प्रश्न 12.
25 cm के सामान्य निकट बिन्दु को कोई व्यक्ति ऐसे संयुक्त सूक्ष्मदर्शी जिसका अभिदृश्यक 8.0 mm फोकस दूरी तथा नेत्रिका 2.5 cm फोकस दूरी की है, का उपयोग करके अभिदृश्यक से 9.0 mm दूरी पर रखे बिम्ब को सुस्पष्ट फोकसित कर लेता है। दोनों लेन्सों के बीच पृथक्कन दूरी क्या है? सूक्ष्मदर्शी की आवर्धन क्षमता क्या है?


प्रश्न 13.
किसी छोटी दूरबीन के अभिदृश्यक की फोकस दूरी 144 cm तथा नेत्रिका की फोकस दूरी 6.0 cm है। दूरबीन की आवर्धन क्षमता कितनी है? अभिदृश्यक तथा नेत्रिका के बीच पृथक्कन दूरी क्या है?
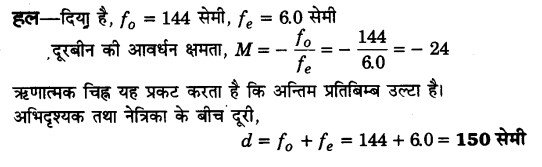
प्रश्न 14.
(a) किसी वेधशाला की विशाल दूरबीन के अभिदृश्यक की फोकस दूरी 15 m है। यदि 1.0 cm फोकस दूरी की नेत्रिका प्रयुक्त की गयी है तो दूरबीन का कोणीय आवर्धन क्या है?
(b) यदि इस दूरबीन का उपयोग चन्द्रमा का अवलोकन करने में किया जाए तो अभिदृश्यक लेन्स द्वारा निर्मित चन्द्रमा के प्रतिबिम्ब का व्यास क्या है? चन्द्रमा का व्यास 3.48 x 106 m तथा चन्द्रमा की कक्षा की त्रिज्या 3.8 x 108 m है।
हल-
दिया है, दूरबीन के अभिदृश्यक लेन्स की फोकस दूरी f0 = 15 मीटर
नेत्रिका की फोकस दूरी fe = 1.0 सेमी = 1.0 x 10-2 मीटर
(a) कोणीय आवर्धन


प्रश्न 15.
दर्पण-सूत्र का उपयोग यह व्युत्पन्न करने के लिए कीजिए कि
(a) किसी अवतल दर्पण के हैं तथा 2f के बीच रखे बिम्ब का वास्तविक प्रतिबिम्ब 2f से दूर बनता है।
(b) उत्तल दर्पण द्वारा सदैव आभासी प्रतिबिम्ब बनता है जो बिम्ब की स्थिति पर निर्भर नहीं करता।
(c) उत्तल दर्पण द्वारा सदैव आकार में छोटा प्रतिबिम्ब, दर्पण के ध्रुव व फोकस के बीच बनता
(d) अवतल दर्पण के ध्रुव तथा फोकस के बीच रखे बिम्ब का आभासी तथा बड़ा प्रतिबिम्ब बनता है।
[नोट: यह अभ्यास आपकी बीजगणितीय विधि द्वारा उन प्रतिबिंबों के गुण व्युत्पन्न करने में सहायता करेगा जिन्हें हम किरण आरेखों द्वारा प्राप्त करते हैं।]




प्रश्न 16.
किसी मेज के ऊपरी पृष्ठ पर जड़ी एक छोटी पिन को 50 cm ऊँचाई से देखा जाता है। 15 cm मोटे आयताकार काँच के गुटके को मेज के पृष्ठ के समान्तर पिन व नेत्र के बीच रखकर उसी बिन्दु से देखने पर पिन नेत्र से कितनी दूर दिखाई देगी? काँच की अपवर्तनांक 1.5 है। क्या उत्तर गुटके की अवस्थिति पर निर्भर करता है?
हल-
काँच का अपवर्तनांक

अतः पिन का विस्थापन x = H – h = 15 सेमी -10 सेमी = 5 सेमी
अर्थात् पिन 5 सेमी उठी प्रतीत होगी।
उत्तर गुटके की अक्ष की स्थिति पर निर्भर नहीं करता।
प्रश्न 17.
निम्नलिखित प्रश्नों के उत्तर लिखिए-
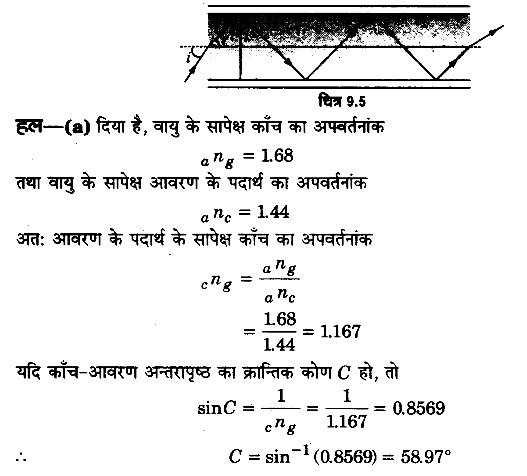
(a) चित्र 9.5 में अपवर्तनांक 1.68 के तन्तु काँच से बनी किसी प्रकाश नलिका (लाइट पाइप) का अनुप्रस्थ परिच्छेद दर्शाया गया है। नलिका का बाह्य आवरण 1.44 अपवर्तनांक के ‘पदार्थ का बना है। नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण परावर्तन होते हैं, ज्ञात कीजिए।
(b) यदि पाइप पर बाह्य आवरण न हो तो क्या उत्तर होगा?

प्रश्न 18.
निम्नलिखित प्रश्नों के उत्तर लिखिए-
(a) आपने सीखा है कि समतल तथा उत्तल दर्पण सदैव आभासी प्रतिबिम्ब बनाते हैं। क्या ये दर्पण किन्हीं परिस्थितियों में वास्तविक प्रतिबिम्ब बना सकते हैं? स्पष्ट कीजिए।
(b) हम सदैव कहते हैं कि आभासी प्रतिबिम्ब को परदे पर केन्द्रित नहीं किया जा सकता। यद्यपि जब हम किसी आभासी प्रतिबिम्ब को देखते हैं तो हम इसे स्वाभाविक रूप में अपनी आँख की स्क्रीन (अर्थात् रेटिना) पर लेते हैं। क्या इसमें कोई विरोधाभास है?
(c) किसी झील के तट पर खड़ा मछुआरा झील के भीतर किसी गोताखोर द्वारा तिरछा देखने पर अपनी वास्तविक लम्बाई की तुलना में कैसा प्रतीत होगा-छोटा अथवा लम्बा?
(d) क्या तिरछा देखने पर किसी जल के टैंक की आभासी गहराई परिवर्तित हो जाती है? यदि हाँ, तो आभासी गहराई घटती है अथवा बढ़ जाती है।
(e) सामान्य काँच की तुलना में हीरे का अपवर्तनांक काफी अधिक होता है? क्या हीरे को तराशने वालों के लिए इस तथ्य का कोई उपयोग होता है?
उत्तर-
(a) यह सही है कि समतल दर्पण तथा उत्तल दर्पण अपने सामने स्थित बिम्ब का आभासी प्रतिबिम्ब बनाते हैं। परन्तु ये दर्पण अपने पीछे स्थित किसी बिन्दु (आभासी बिम्ब) की ओर अभिसरित किरण पुंज को परावर्तित करके अपने सामने स्थित किसी बिन्दु पर अभिसरित कर सकते हैं अर्थात् आभासी बिम्ब का वास्तविक प्रतिबिम्ब बना सकते हैं (देखें चित्र)।
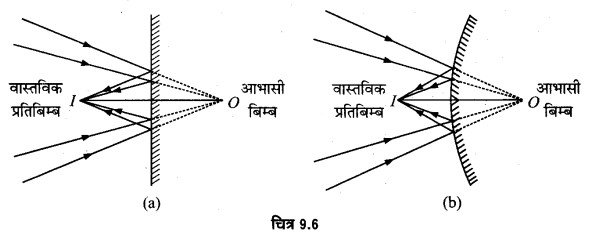
(b) जब किसी दर्पण से परावर्तन अथवा लेन्स से अपवर्तन के पश्चात् किरणें अपसरित होती हैं तो प्रतिबिम्ब को आभासी कहा जाता है। इस प्रतिबिम्ब को परदे पर प्राप्त नहीं किया जा सकता। यदि इन अपसारी किरणों के मार्ग में कोई अन्य दर्पण अथवा लेन्स रखकर इन्हें किसी बिन्दु पर अभिसरित किया जा सकता तो वहाँ वास्तविक प्रतिबिम्ब बनेगा जिसे परदे पर प्राप्त किया जा सकता है। नेत्र लेन्स वास्तव में यही कार्य करता है। यह आभासी प्रतिबिम्ब बनाने वाली अपसारी किरणों को रेटिना पर अभिसरित कर देता है, जहाँ वास्तविक प्रतिबिम्ब बन जाता है। अतः इसमें कोई विरोधाभास नहीं है।
(c) चूंकि इस दशा में अपवर्तन वायु (विरल माध्यम) से पानी (सघन माध्यम) में होता है। अत: झील में डूबे हुए गोताखोर को मछुआरे की लम्बाई अधिक प्रतीत होगी।
(d) हाँ, परिवर्तित हो जाती है। आभासी गहराई घट जाती है।
(e) वायु के सापेक्ष हीरे का अपवर्तनांक 2.42 (काफी अधिक) है तथा क्रान्तिक कोण 24° (बहुत कम) है। हीरा तराशने में दक्ष कारीगर इस तथ्य का उपयोग करते हुए हीरे को इस प्रकार तराशता है, कि एक बार हीरे में प्रवेश करने वाली प्रकाश किरण हीरे के विभिन्न फलकों पर बार-बार परावर्तित होने के बाद ही किसी फलक से बाहर निकल पाए। इसके लिए हीरे की आन्तरिक सतह पर आपतन कोण 24° से अधिक होना चाहिए। इससे हीरा अत्यधिक चमकीला दिखाई पड़ता है।
प्रश्न 19.
किसी कमरे की एक दीवार पर लगे विद्युत बल्ब का किसी बड़े आकार के उत्तल लेन्स द्वारा3 m दूरी पर स्थित सामने की दीवार पर प्रतिबिम्ब प्राप्त करना है। इसके लिए उत्तल लेन्स की अधिकतम फोकस दूरी क्या होनी चाहिए?
हल-
माना किसी उत्तल लेन्स की फोकस दूरी f है तथा यह बल्ब का प्रतिबिम्ब दूसरी दीवार पर बनाता है।
माना बल्ब की लेन्स से दूरी u (आंकिक मान) तथा दूसरी दीवार की लेन्स से दूरी v है, तब
u + v = 3 ⇒ u = 3 – v
लेन्स के सूत्र में चिह्न सहित मान रखने पर,

प्रश्न 20.
किसी परदे को बिम्ब से 90 cm दूर रखा गया है। परदे पर किसी उत्तल लेन्स द्वारा उसे एक-दूसरे से 20 cm दूर स्थितियों पर रखकर, दो प्रतिबिम्ब बनाए जाते हैं। लेन्स की फोकस दूरी ज्ञात कीजिए।
हल-
माना बिम्ब की लेन्स से दूरी u (आंकिक मान) है तथा प्रतिबिम्ब (परदे) की लेन्स से दूरी v है।
u + v = 90 ⇒ v = 90 – u
लेन्स के सूत्र में चिह्न सहित मान रखने पर,

प्रश्न 21.
(a) प्रश्न 10 के दो लेन्सों के संयोजन की प्रभावी फोकस दरी उस स्थिति में ज्ञात कीजिए जब उनके मुख्य अक्ष संपाती हैं तथा ये एक-दूसरे से 8 cm दूरी पर रखे हैं। क्या उत्तर आपतित समान्तर प्रकाश पुंज की दिशा पर निर्भर करेगा? क्या इस तन्त्र के लिए प्रभावी फोकस दूरी किसी भी रूप में उपयोगी है ?
(b) उपर्युक्त व्यवस्था (a) में 1.5 cm ऊँचा कोई बिम्ब उत्तल लेन्स की ओर रखा है। बिम्ब की उत्तल लेन्स से दूरी 40 cm है। दो लेन्सों के तन्त्र द्वारा उत्पन्न आवर्धन तथा प्रतिबिम्ब का आकार ज्ञात कीजिए।




प्रश्न 22.
60° अपवर्तन कोण के प्रिज्म के फलक पर किसी प्रकाशकिरण को किस कोण पर आपतित कराया जाए कि इसका दूसरे फलक से केवल पूर्ण आन्तरिक परावर्तन ही हो? प्रिज्म के पदार्थ का अपवर्तनांक 1.524 है।
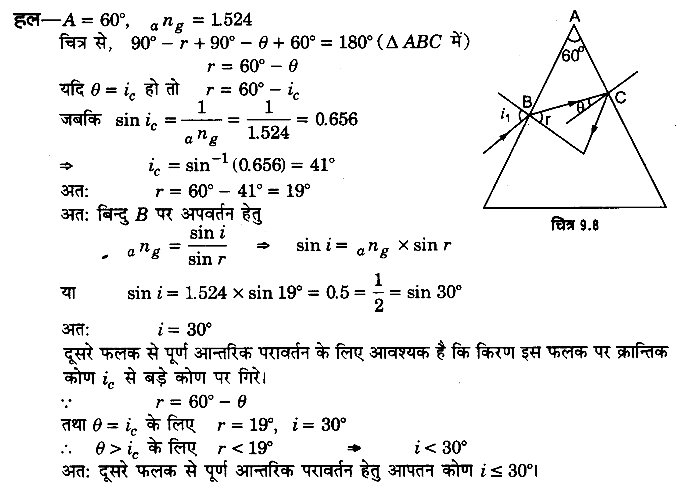
प्रश्न 23.
आपको विविध कोणों के क्राउन काँच व फ्लिंट काँच के प्रिज्म दिए गए हैं। प्रिज्मों का कोई ऐसा संयोजन सुझाइए जो
(a) श्वेत प्रकाश के संकीर्ण पुंज को बिना अधिक परिक्षेपित किए विचलित कर दे।
(b) श्वेत प्रकाश के संकीर्ण पुंज को अधिक विचलित किए बिना परिक्षेपित (तथा विस्थापित)। कर दे।
उत्तर-
हम जानते हैं कि फ्लिण्ट काँच, क्राउन काँच की तुलना में अधिक विक्षेपण उत्पन्न करता है।
(a) बिना विक्षेपण के विचलन उत्पन्न करने हेतु क्राउन काँच का एक प्रिज्म लीजिए तथा एक फ्लिण्टे काँच का प्रिज्म लीजिए जिसका अपवर्तक कोण अपेक्षाकृत कम हो। अब इन्हें एक-दूसरे के सापेक्ष उल्टा रखते हुए सम्पर्क में रखिए। इस प्रकार बना संयोजन श्वेत प्रकाश को बिना अधिक परिक्षेपित किए विचलित कर देगा।
(b) पुराने संयोजन में लिए गए फ्लिण्ट काँच के प्रिज्म के अपवर्तक कोण में वृद्धि कीजिए (परन्तु अभी भी यह कोण दूसरे प्रिज्म की तुलना में कम ही रहेगा)। यह व्यवस्था पुंज को बिना अधिक विचलित किए परिक्षेपण उत्पन्न करेगी।
प्रश्न 24.
सामान्य नेत्र के लिए दूर बिन्दु अनन्त पर तथा स्पष्ट दर्शन का निकट बिन्दु नेत्र के सामने लगभग 25 cm पर होता है। नेत्र का स्वच्छ मण्डल (कॉर्निया) लगभग 40 डायोप्टर की अभिसरण क्षमता प्रदान करता है तथा स्वच्छ मण्डल के पीछे नेत्र लेन्स की अल्पतम अभिसरण क्षमता लगभग 20 डायोप्टर होती है। इस स्थूल आँकड़े से सामान्य नेत्र के परास (अर्थात नेत्र लेन्स की अभिसरण क्षमता का परिसर) का अनुमान लगाइए।
हल-
दिया है, कॉर्निया की अभिसरण क्षमता = +40 D
नेत्र लेन्स की अभिसरण क्षमता = +20 D
अत: कॉर्निया तथा नेत्र लेन्स की कुल अभिसरण क्षमता
P = (40 + 20) D = 60 D
अनन्त पर स्थित वस्तुओं के लिए नेत्र न्यूनतम अभिसरण क्षमता का प्रयोग करता है।
अत: उपर्युक्त क्षमता न्यूनतम अभिसरण क्षमता होगी। इसलिए नेत्र लेन्स की अधिकतम फोकस दूरी

प्रश्न 25.
क्या निकट दृष्टिदोष अथवा दीर्घ दृष्टिदोष आवश्यक रूप से यह ध्वनित होता है कि नेत्र ने अपनी समंजन क्षमता आंशिक रूप से खो दी है? यदि नहीं, तो इन दृष्टिदोषों का क्या कारण हो सकता है?
हल-
यह आवश्यक नहीं है कि निकट दृष्टिदोष अथवा दूर दृष्टिदोष केवल नेत्र के आंशिक रूप से अपनी समंजन क्षमता खो देने के कारण ही उत्पन्न होता है। यह नेत्र गोलक के सामान्य आकार से बड़ा अथवा छोटा होने के कारण भी उत्पन्न हो सकता है।
प्रश्न 26.
निकट दृष्टिदोष का कोई व्यक्ति दूर दृष्टि के लिए -1.0 D क्षमता का चश्मा उपयोग कर रहा है। अधिक आयु होने पर उसे पुस्तक पढ़ने के लिए अलग से +2.0 D क्षमता के चश्मे की आवश्यकता होती है। स्पष्ट कीजिए ऐसा क्यों हुआ?
हल-
– 1.0 D क्षमता के संगत फोकस दूरी

अत: प्रारम्भ में नेत्र की स्वस्थ अवस्था में व्यक्ति 1.00 मीटर दूरी तक की वस्तुओं को स्पष्ट देख सकता है।
अधिक आयु होने पर नेत्र की समंजन क्षमता कम हो जाने के कारण नेत्र लेन्स का निकट बिन्दु और दूर विस्थापित हो जाता है। अत: व्यक्ति में जरा दृष्टि दोष है। इस दशा में प्रयुक्त उत्तल लेन्स की क्षमता

चूँकि निकट बिन्दु 25 सेमी से 50 सेमी पर विस्थापित हो गया है, अतः जरी दृष्टि दोष से पीड़ित व्यक्ति 50 सेमी से 100 सेमी तक के बीच की वस्तु देख सकता है।
प्रश्न 27.
कोई व्यक्ति ऊर्ध्वाधर तथा क्षैतिज धारियों की कमीज पहने किसी दूसरे व्यक्ति को देखता है। वह क्षैतिज धारियों की तुलना में ऊर्ध्वाधर धारियों को अधिक स्पष्ट देख पाता है। ऐसा किस दृष्टिदोष के कारण होता है? इस दृष्टिदोष का संशोधन कैसे किया जाता है?
हल-
यह घटना अबिन्दुकता नामक दृष्टिदोष के कारण होती है। सामान्य नेत्र पूर्णतः गोलीय होता है। तथा इसके विभिन्न तलों की वक्रता सर्वत्र समान होती है। परन्तु अबिन्दुकता दोष में कॉर्निया पूर्णतः गोलीय नहीं रह जाता तथा इसके विभिन्न तलों की वक्रताएँ समान नहीं रह पातीं। प्रश्नानुसार व्यक्ति ऊध्र्वाधर धारियों को स्पष्ट देख पाता है परन्तु क्षैतिज धारियों को नहीं। इससे स्पष्ट है कि नेत्र में ऊर्ध्वाधर तल में पर्याप्त वक्रता है जिसके कारण ऊर्ध्वाधर रेखाएँ दृष्टि पटल पर स्पष्ट फोकस हो रही हैं। परन्तु क्षैतिज तल की वक्रता पर्याप्त नहीं है। इस दोष को सिलिण्डरी लेन्स की सहायता से दूर किया जा सकता है।
प्रश्न 28.
कोई सामान्य निकट बिन्दु (25 cm) का व्यक्ति छोटे अक्षरों में छपी वस्तु को 5 cm फोकस दूरी के पतले उत्तल लेन्स के आवर्धक लेन्स का उपयोग करके पढ़ता है।
(a) वह निकटतम तथा अधिकतम दूरियाँ ज्ञात कीजिए जहाँ वह उस पुस्तक को आवर्धक लेन्स द्वारा पढ़ सकता है।
(b) उपर्युक्त सरल सूक्ष्मदर्शी के उपयोग द्वारा संभावित अधिकतम तथा न्यूनतम कोणीय आवर्धन (आवर्धन क्षमता) क्या है?
हल-
(a) वस्तु को निकटतम दूरी से देखने के लिए वस्तु का प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी अर्थात् निकट बिन्दु पर बनना चाहिए। अत: v = -25 सेमी
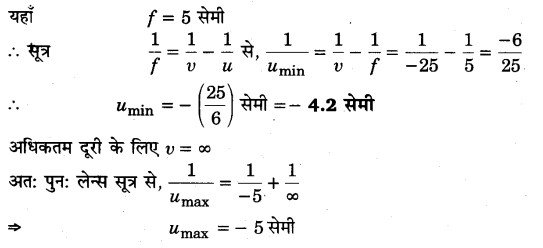

प्रश्न 29.
कोई कार्ड शीट जिसे 1 mm2 साइज़ के वर्गों में विभाजित किया गया है, को 9 cm दूरी पर रखकर किसी आवर्धक लेन्स (10 cm फोकस दूरी का अभिसारी लेन्स) द्वारा उसे नेत्र के निकट रखकर देखा जाता है।
(a) लेन्स द्वारा उत्पन्न आवर्धन (प्रतिबिम्ब-साइज़/वस्तु-साइज़) क्या है? आभासी प्रतिबिम्ब में प्रत्येक वर्ग का क्षेत्रफल क्या है?
(b) लेन्स का कोणीय आवर्धन (आवर्धन क्षमता) क्या है?
(c) क्या (a) में आवर्धन क्षमता (b) में आवर्धन के बराबर है? स्पष्ट कीजिए।
हल-
(a) दिया है, u = -9 सेमी, f = +10 सेमी

(c) बराबर नहीं है; क्योंकि लेन्स द्वारा उत्पन्न ‘आवर्धन तथा लेन्स की आवर्धन क्षमता अलग-अलग भौतिक राशियाँ हैं। ये तभी बराबर होंगी यदि प्रतिबिम्ब नेत्र के निकट बिन्दु (= 25 सेमी) पर बने।
प्रश्न 30.
(a) प्रश्न 29 में लेन्स को चित्र से कितनी दूरी पर रखा जाए ताकि वर्गों को अधिकतम संभव आवर्धन क्षमता के साथ सुस्पष्ट देखा जा सके।
(b) इस उदाहरण में आवर्धन (प्रतिबिम्ब-साइज़/वस्तु-साइज़) क्या है?
(c) क्या इस प्रक्रम में आवर्धन, आवर्धन क्षमता के बराबर है? स्पष्ट कीजिए।
हल-
(a) अधिकतम आवर्धन क्षमता के लिए, v = D = -25 cm, f = 10 सेमी

हाँ, इस स्थिति में आवर्धन, आवर्धन क्षमता के बराबर है, क्योंकि प्रतिबिम्ब नेत्र के निकट बिन्दु D = 25 सेमी पर बनता है।
प्रश्न 31.
प्रश्न 30 में वस्तु तथा आवर्धक लेन्स के बीच कितनी दूरी होनी चाहिए ताकि आभासी प्रतिबिम्ब में प्रत्येक वर्ग 6.25 mm क्षेत्रफल का प्रतीत हो? क्या आप आवर्धक लेन्स को नेत्र के अत्यधिक निकट रखकर इन वर्गों को सुस्पष्ट देख सकेंगे।
[नोट: अभ्यास 9.29 से 9.31 आपको निरपेक्ष साइज में आवर्धन तथा किसी यन्त्र की आवर्धन क्षमता (कोणीय आवर्धन) के बीच अन्तर को स्पष्टतः समझने में सहायता करेंगे।]
हल-
दिया है, f = 10 सेमी, वस्तु के प्रत्येक वर्ग को क्षेत्रफल A0 = 1 मिमी2
प्रतिबिम्ब के प्रत्येक वर्ग का क्षेत्रफल, Al = 6.25 मिमी2
क्षेत्रीय आवर्धन,

चूंकि आभासी प्रतिबिम्ब 15 सेमी पर है तथा स्पष्ट दृष्टि की न्यूनतम दूरी 25 सेमी है। अत: प्रतिबिम्ब नेत्र को सुस्पष्ट दिखाई नहीं देगा।
प्रश्न 32.
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) किसी वस्तु द्वारा नेत्र पर अन्तरित कोण आवर्धक लेन्स द्वारा उत्पन्न आभासी प्रतिबिम्ब द्वारा नेत्र पर अन्तरित कोण के बराबर होता है। तब.फिर किन अर्थों में कोई आवर्धक लेन्स कोणीय आवर्धन प्रदान करता है?
(b) किसी आवर्धक लेन्स से देखते समय प्रेक्षक अपने नेत्र को लेन्स से अत्यधिक सटाकर रखता है। यदि प्रेक्षक अपने नेत्र को पीछे ले जाए तो क्या कोणीय आवर्धन परिवर्तित हो जाएगा?
(c) किसी सरल सूक्ष्मदर्शी की आवर्धन क्षमता उसकी फोकस दूरी के व्युत्क्रमानुपाती होती है। तब हमें अधिकाधिक आवर्धन क्षमता प्राप्त करने के लिए कम-से-कम फोकस दूरी के उत्तल लेन्स का उपयोग करने से कौन रोकता है?
(d) किसी संयुक्त सूक्ष्मदर्शी के अभिदृश्यक लेन्स तथा नेत्रिका लेन्स दोनों ही की फोकस दूरी कम क्यों होनी चाहिए?
(e) संयुक्त सूक्ष्मदर्शी द्वारा देखते समय सर्वोत्तम दर्शन के लिए हमारे नेत्र, नेत्रिका पर स्थित न होकर उससे कुछ दूरी पर होने चाहिए। क्यों? नेत्र तथा नेत्रिका के बीच की यह अल्प दूरी कितनी होनी चाहिए?
उत्तर-
(a) आवर्धक लेन्स के बिना वस्तु को देखते समय उसे नेत्र से 25 cm से कम दूरी पर नहीं रखा जा सकता, परन्तु लेन्स की सहायता से वस्तु को देखते समय वस्तु को अपेक्षाकृत नेत्र के अधिक समीप रखा जा सकता है जिससे कि अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बने। इस प्रकार कोणीय साइज में वृद्धि वस्तु को नेत्र के समीप रखने के कारण होती है।
(b) हाँ, क्योंकि इस स्थिति में प्रतिबिम्ब द्वारा नेत्र पर बना दर्शन कोण, उसके द्वारा लेन्स पर बने दर्शन कोण से कुछ छोटा हो जाएगा।
(c) एक-तो अत्यन्त कम फोकस दूरी के लेन्सों (मोटे लेन्सों) को बनाने की प्रक्रिया आसान नहीं है, दूसरे फोकस दूरी घटने के साथ लेन्सों में विपथन का दोष बढ़ने लगती है। इससे उनके द्वारा बने प्रतिबिम्ब अस्पष्ट हो जाते हैं। व्यवहार में किसी एकल उत्तल लेन्स द्वारा 3 से अधिक आवर्धन प्राप्त करना सम्भव नहीं है परन्तु विपथन के दोष से मुक्त लेन्स द्वारा कहीं अधिक आवर्धन (लगभग 10) प्राप्त किया जा सकता है।

(e) संयुक्त सूक्ष्मदर्शी में वस्तु से चलने वाला प्रकाश अभिदृश्यक से गुजरने के बाद नेत्रिका से गुजरकर आँख तक पहुँचता है। वस्तु का प्रतिबिम्ब स्पष्ट देखने के लिए आवश्यक है कि वस्तु से चलने वाला अधिकतम प्रकाश नेत्र में पहुँचे। वस्तु से चलने वाले प्रकाश को अधिकतम मात्रा में ग्रहण करने के लिए ही नेत्र को नेत्रिका से अत्यल्प दूरी पर रखा जाता है। यह अत्यल्प दूरी यन्त्र की संरचना पर निर्भर करती है तथा उस पर लिखी गई होती है।
प्रश्न 33.
1.25 cm फोकस दूरी का अभिदृश्यक तथा 5 cm फोकस दूरी की नेत्रिका का उपयोग करके वांछित कोणीय आवर्धन (आवर्धन क्षमता) 30X होता है। आप संयुक्त सूक्ष्मदर्शी का समायोजन कैसे करेंगे?
हल-
जब अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है तो यह संयुक्त सूक्ष्मदर्शी का सामान्य समायोजन होता है। इसमें


अतः संयुक्त सूक्ष्मदर्शी के समायोजन में अभिदृश्यक तथा नेत्रिका को परस्पर 11.67 सेमी दूरी पर रखना होगा तथा वस्तु को अभिदृश्यक के सामने इससे 1.5 सेमी की दूरी पर रखना होगा।
प्रश्न 34.
किसी दूरबीन के अभिदृश्यक की फोकस दूरी 140 cm तथा नेत्रिका की फोकस दूरी 5.0 cm है। दूर की वस्तुओं को देखने के लिए दूरबीन की आवर्धन क्षमता क्या होगी जब-
(a) दूरबीन का समायोजन सामान्य है (अर्थात अन्तिम प्रतिबिम्ब अनन्त पर बनता है)।
(b) अन्तिम प्रतिबिम्ब स्पष्ट दर्शन की अल्पतम दूरी (25 cm) पर बनता है।

प्रश्न 35.
(a) प्रश्न 34 (a) में वर्णित दूरबीन के लिए अभिश्यक लेन्स तथा नेत्रिका के बीच पृथक्कन दूरी क्या है?
(b) यदि इस दूरबीन का उपयोग 3 km दूर स्थित 100 m ऊँची मीनार को देखने के लिए किया जाता है तो अभिदृश्यक द्वारा बने मीनार के प्रतिबिम्ब की ऊँचाई क्या है?
(c) यदि अन्तिम प्रतिबिम्ब 25 cm दूर बनता है तो अन्तिम प्रतिबिम्ब में मीनार की ऊँचाई क्या है?

प्रश्न 36.
किसी कैसेग्रेन दूरबीन में चित्र 9.9 में दर्शाए अनुसार दो दर्पणों का प्रयोग किया। द्वतीयक गया है। इस दूरबीन में दोनों दर्पण एक-दूसरे से 20 mm दूर रखे गए हैं। यदि बड़े दर्पण की वक्रता त्रिज्या 220 mm हो तथा छोटे दर्पण की वक्रता त्रिज्या 140 mm हो तो अनन्त पर रखे चित्र 9.9 किसी बिम्ब का अन्तिम प्रतिबिम्ब कहाँ बनेगा?
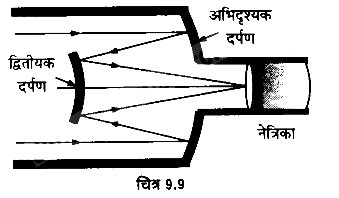

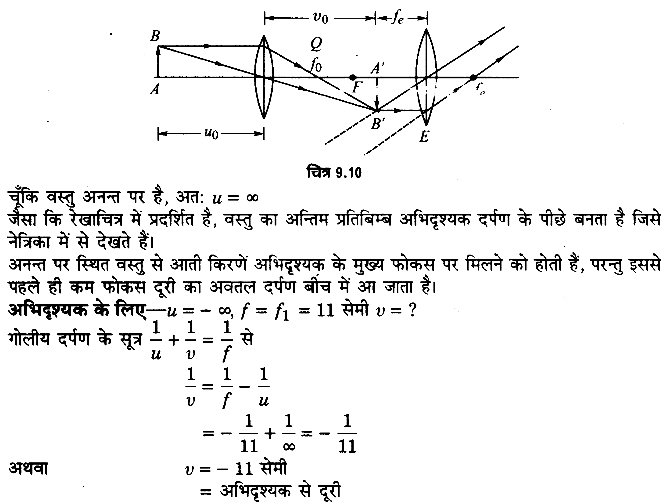

प्रश्न 37.
किसी गैल्वेनोमीटर की कुण्डली से जुड़े समतल दर्पण पर लम्बवत आपतित प्रकाश (चित्र 9.11) दर्पण से टकराकर अपना पथ पुनः अनुरेखित करता है। गैल्वेनोमीटर की कुण्डली में प्रवाहित कोई धारा दर्पण में 3.5° का परिक्षेपण उत्पन्न करती है। दर्पण के सामने 1.5 m की दूरी पर रखे परदे पर प्रकाश के परावर्ती चिह्न में कितना विस्थापन होगा?


प्रश्न 38.
चित्र 9.12 में कोई समोत्तल लेन्स (अपवर्तनांक 1.50) किसी समतल दर्पण के फलक पर किसी द्रव की परत के सम्पर्क में दर्शाया गया है। कोई छोटी सुई जिसकी नोक मुख्य अक्ष पर है, अक्ष के अनुदिश ऊपर-नीचे गति कराकर इस प्रकार समायोजित की जाती है कि सुई की नोक का उल्टा प्रतिबिम्ब सुई की स्थिति पर ही बने। इस स्थिति में सुई की लेन्स से दूरी 45.0 cm है। द्रव को हटाकर प्रयोग को दोहराया जाता है। नयी दूरी 30.0 cm मापी जाती है। द्रव का काम अपवर्तनांक क्या है?
हुल-
द्रव को हटाकर प्रयोग करते समय इस स्थिति में सुई से चलने वाली किरणें काँच के लेन्स से अपवर्तित होकर समतल दर्पण पर अभिलम्बवत् आपतित होती हैं। दर्पण इन किरणों को वापस उन्हीं के मार्ग पर लौटा देता है जिससे किरणें वापस सुई की स्थिति में ही प्रतिबिम्ब बनाती हैं।
यह स्पष्ट है कि दर्पण की अनुपस्थिति में लेन्स से अपवर्तित किरणें अनन्त पर मिलती हैं।



परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न
प्रश्न 1.
अपवर्तन की घटना में निम्न में से कौन-सी राशि अपरिवर्तित रहती है? (2012)
(i) प्रकाश की चाल
(ii) प्रकाश की तीव्रता
(iii) प्रकाश की तरंगदैर्घ्य
(iv) प्रकाश की आवृत्ति
उत्तर-
(iv) प्रकाश की आवृत्ति
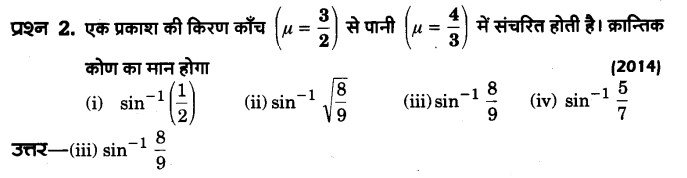
प्रश्न 3.
आकाश नीला दिखाई देता है- (2014, 17)
(i) प्रकीर्णन के कारण
(ii) परावर्तन के कारण
(iii) अपवर्तन के कारण
(iv) पूर्ण आन्तरिक परावर्तन के कारण
उत्तर-
(i) प्रकीर्णन के कारण
प्रश्न 4.
निरपेक्ष अपवर्तनांक का मान है-
(i) n < 1
(ii) n > 1
(iii) 1 > n > 0
(iv) ∞ > n > 0
उत्तर-
(ii) n > 1
प्रश्न 5.
एक उत्तल दर्पण की फोकस दूरी 20 सेमी है। एक वस्तु दर्पण के सामने ध्रुव से 20 सेमी की दूरी पर रखे जाने पर प्रतिबिम्ब की दूरी ध्रुव से होती है- (2014)
(i) 40 सेमी
(ii) 10 सेमी
(iii) 20 सेमी
(iv) अनन्त पर
उत्तर-
(ii) 10 सेमी
प्रश्न 6.
यदि किसी माध्यम से निर्वात में सम्पूर्ण आन्तरिक परावर्तन के लिए क्रान्तिक कोण 30° है, तो माध्यम में प्रकाश का वेग है- (2015, 17)
(i) 3 x 108 भी/से
(ii) 1.5 x 108 मी/से।
(iii) 6 x 108 मी/से
(iv) 4.5 x 108 मी/से
उत्तर-
(ii) 1.5 x 108 मी/से
प्रश्न 7.
यदि सघन माध्यम में आपतन कोण, क्रान्तिक कोण के बराबर हो, तो अपवर्तन कोण होगा- (2016, 17)
(i) 0°
(ii) 45°
(iii) 90°
(iv) 180°
उत्तर-
(iii) 90°
प्रश्न 8.
यदि विरल तथा सघन माध्यम में प्रकाश की चाल क्रमशः v1 तथा v2 हों तथा सघन माध्यम में क्रांतिक कोण C है, तब (2016)
(i) v1 = v2 sinC
(ii) v1 = v2 cosC
(iii) v1 = v2 tanC
(iv) v1 = v2 cosec C
उत्तर-
(iv) v1 = v2 cosec C
प्रश्न 9.
वायु के सापेक्ष जल और काँच के अपवर्तनांक क्रमशः एवं हैं। काँच का जल के सापेक्ष अपवर्तनांक होगा- (2017)
(i)
(ii)
(iii)
(iv)
उत्तर-
(iii)
प्रश्न 10.
वायु में प्रकाश की चाल 3.0 x 108 मीटर/सेकण्ड है। 1.5 अपवर्तनांक वाले काँच में प्रकाश की चाल होगी- (2017)
(i) 1.5 x 108 मी/से।
(ii) 2.0 x 108 मी/से
(iii) 1.8 x 108 मी/से
(iv) 2.5 x 108 मी/से
उत्तर-
(ii) 2.0 x 108 मी/से
प्रश्न 11.
किसी गोलीय दर्पण की फोकस दूरी (f) एवं वक्रता त्रिज्या (R) में सम्बन्ध है- (2017)
(i) R =
(ii) f = 3R
(ii) f =
(iv) f =
उत्तर-
(iii)
प्रश्न 12.
दो लेन्स जिनकी क्षमताएँ 5D तथा -3D हैं, सम्पर्क में रखे हैं। संयुक्त लेन्स की फोकस दूरी है- (2012, 13, 15)
(i) 50 सेमी
(ii) 75 सेमी
(iii) 25 सेमी
(iv) 20 सेमी
उत्तर-
(i) 50 सेमी
प्रश्न 13.
4 डायोप्टर और -2 डायोप्टर क्षमता के दो लेन्स सम्पर्क में रखे हैं। संयुक्त लेन्स की फोकस दूरी होगी- (2013, 16, 17)
(i) 50 सेमी
(ii)-50 सेमी
(iii) 25 सेमी
(iv) -25 सेमी
उत्तर-
(i) 50 सेमी
प्रश्न 14.
एक समतल-उत्तल लेन्स में उत्तल पृष्ठ की वक्रता-त्रिज्या 10 सेमी और लेन्स की फोकस दूरी 30 सेमी है। लेन्स के पदार्थ का अपवर्तनांक है- (2011)
(i) 1.5
(ii) 1.66
(iii) 1.33
(iv) 0.3
उत्तर-
(iii) 1.33
प्रश्न 15.
सम्पर्क में रखे दो पतले लेन्सों की फोकस दूरियाँ 25 सेमी तथा -40 सेमी हैं। इस संयोजन की क्षमता होगी- (2010)
(i) -6.67 D
(ii) -2.5 D
(iii) +1.5 D
(iv) +4 D
उत्तर-
(iii) + 1.5 D
प्रश्न 16.
सम्पर्क में रखे उत्तल एवं अवतल लेन्स की फोकस दूरियाँ क्रमशः 12 सेमी और 18 सेमी हैं। संयुक्त लेन्स की फोकस दूरी होगी- (2014)
(i) 50 सेमी
(ii) 45 सेमी
(iii) 36 सेमी
(iv) 18 सेमी
उत्तर-
(iv) 18 सेमी
प्रश्न 17.
0.5 मी फोकस दूरी के एक उत्तल लेन्स को 1 मी फोकस दूरी के अवतल लेन्स के सम्पर्क में रखा गया है। संयुक्त लेन्स की फोकस दूरी है- (2010)
(i) 1 मी।
(ii) -1 मी
(iii) 0.5 मी
(iv) -0.5 मी
उत्तर-
(i) 1 मी
प्रश्न 18.
एक पदार्थ जिसका अपवर्तनांक n = 1.51 है, से एक पतला लेन्स बना है। लेन्स की दोनों सतह उत्तल हैं। इसे जल (n = 1.33) में डुबोया गया है। यह लेन्स व्यवहार करेगा- (2010)
(i) एक अभिसारी लेन्स की तरह
(ii) एक अपसारी लेन्स की तरह
(iii) काँच के एक आयताकार टुकड़े की तरह
(iv) एक प्रिज्म की तरह
उत्तर-
(i) एक अभिसारी लेन्स की तरह
प्रश्न 19.
यदि 1.5 अपवर्तनांक के समोत्तल लेन्स की वक्रता-त्रिज्या 10 सेमी, हो तो इस लेन्स की क्षमता होगी- (2011)
(i) 10D
(ii) 5D
(iii) -10D
(iv) -5D
उत्तर-
(ii) 5D
प्रश्न 20.
एक उत्तल लेन्स की क्षमता 2 डायोप्टर है। इसकी फोकस-दूरी होगी- (2015)
(i) 20 सेमी
(ii) 50 सेमी
(iii) 40 सेमी
(iv) 60 सेमी
उत्तर-
(ii) 50 सेमी
प्रश्न 21.
एक उत्तल लेन्स मुख्य अक्ष पर रखी बिन्दु वस्तु का वास्तविक प्रतिबिम्ब बनाता है। यदि लेन्स के ऊपरी अर्द्ध भाग को काला कर दिया जाए, तो (2012)
(i) प्रतिबिम्ब नीचे की ओर खिसक जायेगा।
(ii) प्रतिबिम्ब ऊपर की ओर खिसक जायेगा
(iii) प्रतिबिम्ब की लम्बाई आधी हो जायेगी
(iv) प्रतिबिम्ब की तीव्रता घट जायेगी
उत्तर-
(iv) प्रतिबिम्ब की तीव्रता घट जायेगी।
प्रश्न 22.
+3D तथा -5D क्षमता के दो पतले लेन्स सम्पर्क में रखे गये हैं। इस संयोजन की फोकस दूरी होगी- (2009, 16)
(i) -40 सेमी
(ii) +40 सेमी
(iii) +20 सेमी
(iv) -50 सेमी
उत्तर-
(iv) -50 सेमी
प्रश्न 23.
R वक्रता त्रिज्या तथा n अपवर्तनांक का एक समतल-उत्तल लेन्स R वक्रता त्रिज्या n1 तथा n2 अपवर्तनांक के समतल-अवतल लेन्स के सम्पर्क में चित्रानुसार रखे जाते हैं। संयुक्त लेन्स की क्षमता है- (2017)
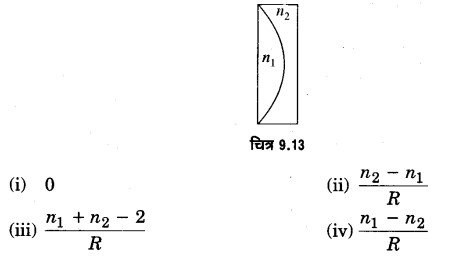
उत्तर-
(i) 0
प्रश्न 24.
दो लेन्स जिनकी शक्तियाँ 4D और -2D हैं, सम्पर्क में रखे हैं। संयुक्त लेन्स की शक्ति- (2017)
(i) 6 D
(ii) 2 D
(iii) -2 D
(iv) 4 D
उत्तर-
(ii) 2 D
प्रश्न 25.
एक प्रिज्म का अपवर्तक कोण 60° है। जब प्रकाश की एक किरण 50° पर आपतित होती है तो इसमें अल्पतम विचलन होता है। अल्पतम विचलन कोण का मान है- (2013)
(i) 40°
(ii) 45°
(iii) 55°
(iv) 60°
उत्तर-
(i) 40°
प्रश्न 26.
एक समबाहु प्रिज्म न्यूनतम विचलन की स्थिति में है। यदि आपतन कोण प्रिज्म कोण का 4/5 गुना हो, तो न्यूनतम विचलन कोण का मान होगा- (2011)
(i) 72°
(ii) 60°
(iii) 48°
(iv) 36°
उत्तर-
(iv) 36°
प्रश्न 27.
प्रिज्म से गुजरने पर निम्नलिखित में से किस रंग के प्रकाश का विचलन अधिकतम होगा?
(i) लाल रंग
(ii) बैंगनी रंग
(iii) नीला रंग
(iv) हरा रंग
उत्तर-
(ii) बैंगनी रंग
प्रश्न 28.
जिस भौतिक घटना के लिए सर सी० वी० रमन को नोबल पुरस्कार प्रदान किया गया था, वह है प्रकाश का- (2014)
(i) ध्रुवण
(ii) व्यतिकरण
(ii) विवर्तन
(iv) प्रकीर्णन
उत्तर-
(iv) प्रकीर्णन
प्रश्न 29.
निम्नलिखित में से किस रंग के प्रकाश की चाल जल में सर्वाधिक होगी?
(i) लाल
(ii) पीला
(iii) हरा
(iv) बैंगनी
उत्तर-
(i) लाल
प्रश्न 30.
उदय व अस्त होते समय सूर्य का ताम्र वर्ण (रक्ताभ) दिखना सम्बन्धित है, प्रकाश के
(i) प्रकीर्णन से
(ii) परिक्षेपण से
(iii) अपवर्तन से
(iv) व्यतिकरण से
उत्तर-
(i) प्रकीर्णन से
प्रश्न 31.
एक व्यक्ति +2D क्षमता का चश्मा प्रयोग करता है। उसका दृष्टि दोष है- (2014)
(i) निकट दृष्टि दोष ।
(ii) दूर दृष्टि दोष,
(ii) जरा दूर दृष्टि दोष ।
(iv) अबिन्दुकता
उत्तर-
(ii) दूर दृष्टि दोष
प्रश्न 32.
सामान्य नेत्र के लिए स्पष्ट दृष्टि की न्यूनतम दूरी है- (2015)
(i) अनन्त
(ii) 50 सेमी
(iii) 25 सेमी
(iv) 75 सेमी
उत्तर-
(iii) 25 सेमी
प्रश्न 33.
इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन क्षमता प्रकाशिक सूक्ष्मदर्शी की अपेक्षा अधिक होती है- (2011)
(i) 5 गुनी
(ii) 50 गुनी
(iii) 500 गुनी
(iv) 5000 गुनी
उत्तर-
(iv) 5000 गुनी
प्रश्न 34.
नेत्र लेन्स की प्रकृति होती है- (2016)
(i) अभिसारी
(ii) अपसारी.
(iii) अभिसारी तथा अपसारी दोनों
(iv) इनमें से कोई नहीं
उत्तर-
(i) अभिसारी
प्रश्न 35.
निकट दृष्टि दोष से पीड़ित व्यक्ति के लिए प्रयुक्त किया जाता है
(i) अवतल लेन्स
(ii) अवतल दर्पण
(iii) उत्तल दर्पण
(iv) उत्तल लेन्स
उत्तर-
(i) अवतल लेन्स
प्रश्न 36.
दूर दृष्टि दोष से पीड़ित व्यक्ति के लिए प्रयुक्त किया जाता है
(i) अवतल लेन्स
(ii) अवतल दर्पण
(iii) उत्तल दर्पण
(iv) उत्तल लेन्स
उत्तर-
(iv) उत्तल लेन्स
प्रश्न 37.
किसी दूरदर्शी के अभिदृश्यक लेन्स का व्यास D है। यदि प्रयुक्त प्रकाश की तरंगदैर्घ्य λ हो, तो इसकी विभेदन क्षमता होगी- (2010, 12, 13)
(i) λ/D
(ii) 1.22λ/D
(iii) D/1.22λ
(iv) λD
उत्तर-
(iii) D/1.22λ
प्रश्न 38.
दूर-दृष्टि दोष से पीड़ित व्यक्ति का निकट बिन्दु स्थित होगा- (2014)
(i) 25 सेमी दूरी पर
(ii) 25 सेमी से कम दूरी पर
(iii) 25 सेमी से अधिक दूरी पर
(iv) अनन्त पर
उत्तर-
(iii) 25 सेमी से अधिक दूरी पर
प्रश्न 39.
एक खगोलीय दूरदर्शी की आवर्धन क्षमता 10 तथा नेत्रिका की फोकस दूरी 20 सेमी है। अभिदृश्यक लेन्स की फोकस दूरी है- (2017)
(i) 2 सेमी
(ii) 200 सेमी
(ii) 100 सेमी
(iv) 0.5 सेमी
उत्तर-
(ii) 200 सेमी
प्रश्न 40.
एक दूरदर्शी के अभिदृश्यक लेन्स का व्यास 0.1 मीटर है तथा प्रकाश की तरंगदैर्घ्य 600 नैनोमीटर है। दूरदर्शी की विभेदन सीमा होगी लगभग- (2017)
(i) 7.32 x 10-4 रेडियन
(ii) 6.0 x 10-5 रेडियन
(iii) 7.32 x 10-6 रेडियन
(iv) 6 x 10-2 रेडियन
उत्तर-
(iii) 7.32 x 10-6 रेडियन
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
आवर्धन का सूत्र
(i) v व u के पदों में
(ii) u वीं के पदों में,
(iii) v तथा f के पदों में लिखिए।

प्रश्न 2.
अपवर्तनांक की परिभाषा दीजिए।
उत्तर-
आपतन कोण की ज्या तथा अपवर्तन कोण की ज्या का अनुपात एक नियतांक होता है। जिसे पहले माध्यम के सापेक्ष दूसरे माध्यम का अपवर्तनांक कहते हैं।
– नियतांक
प्रश्न 3.
प्रकाश के वेग के पदों में अपवर्तनांक का सूत्र लिखिए।

प्रश्न 4.
क्रान्तिक कोण की परिभाषा लिखिए। (2017)
उत्तर-
सघन माध्यम में बना वह आपतन कोण जिसके लिए विरल माध्यम में अपवर्तन कोण 90° हो, क्रान्तिक कोण कहलाता है।
प्रश्न 5.
उस भौतिक सिद्धान्त का नाम लिखिए जिस पर प्रकाशिक तन्तु का कार्य सिद्धान्त आधारित है। (2018)
उत्तर-
पूर्ण आन्तरिक परावर्तन।
प्रश्न 6.
विरल माध्यम के सापेक्ष सघन माध्यम के अपवर्तनांक तथा क्रान्तिक कोण में सम्बन्ध लिखिए।
उत्तर-
=
जहाँ, C = क्रान्तिक कोण तथा । विरल और d सघन माध्यम का संकेत है।
प्रश्न 7.
यदि प्रकाश की एक किरण हवा से काँच के पृष्ठ पर 45° पर आपतित हो तो यह 15° विचलित होती है। काँच-हवा पृष्ठ के लिए क्रान्तिक कोण की गणना कीजिए। (2014)
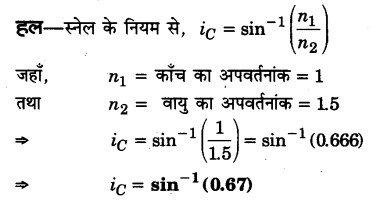
प्रश्न 8.
अवतल दर्पण के उपयोग लिखिए।
उत्तर-
- हजामत करने में,
- डॉक्टर द्वारा शरीर के सूक्ष्म भागों की जाँच करने में,
- कार की हेडलाइट में, टॉर्च में तथा टेबल लैम्पों के शेड में परावर्तक के रूप में।
प्रश्न 9.
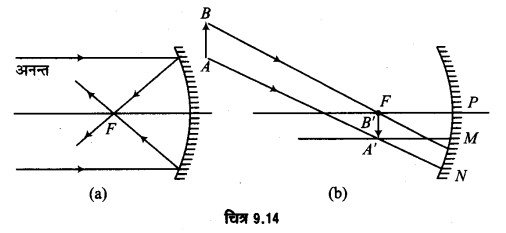
अवतल दर्पण द्वारा अनन्त पर स्थित वस्तु के प्रतिबिम्ब को किरण आरेख द्वारा दर्शाइए। (2014)
उत्तर-
अवतल दर्पण द्वारा अनन्त पर स्थित वस्तु के प्रतिबिम्ब को चित्र 9.14 में प्रदर्शित किया गया है।
प्रश्न 10.
किसी समतल परावर्ती तल पर 5000 Å का प्रकाश आपतित है। परावर्तित प्रकाश की आवृत्ति ज्ञात कीजिए। (2015)

प्रश्न 11.
गोलीय दर्पण की फोकस दूरी की परिभाषा दीजिए। एक अवतल दर्पण अपने सामने से 10 सेमी दूरी पर रखी वस्तु का 3 गुना वास्तविक प्रतिबिम्ब बनाता है। दर्पण की वक्रता त्रिज्या ज्ञात कीजिए। (2016)
उत्तर-
दर्पण के ध्रुव से मुख्य फोकस तक की दूरी को गोलीय दर्पण की फोकस दूरी कहते हैं।
यहाँ, u = -10 सेमी
माना O = x होगी।
I = 3x सेमी
हम जानते हैं कि,

प्रश्न 12.
15 सेमी फोकस दूरी वाले एक अवतल दर्पण के सामने दर्पण से 10 सेमी दूरी पर 8 सेमी ऊँचाई की वस्तु रखी है। दर्पण द्वारा बने प्रतिबिम्ब की स्थिति ज्ञात कीजिए। (2016)

प्रश्न 13.
वायु के सापेक्ष पानी तथा काँच के अपवर्तनांक क्रमशः तथा
हैं। काँच से पानी पर आपतित प्रकाश किरण के लिए क्रान्तिक कोण का मान ज्ञात कीजिए। (2017)

प्रश्न 14.
किसी लेन्स के लिए न्यूटन का सूत्र लिखिए तथा प्रतीकों के अर्थ बताइए। (2013, 14, 17)
उत्तर-
x’x = ff’, जहाँ x’ तथा x क्रमश: प्रथम एवं द्वितीय फोकस से वस्तु की दूरियाँ एवं f’ तथा f क्रमशः लेन्स की प्रथम तथा द्वितीय फोकस दूरियाँ हैं।
प्रश्न 15.
लेन्स की फोकस दूरी का सूत्र लिखिए, जबकि लेन्स के दोनों ओर के माध्यम भिन्न-भिन्न हैं। (2013)

प्रश्न 16.
एक लेन्स की क्षमता + 2.5 डायोप्टर है? लेन्स की फोकस दूरी ज्ञात कीजिए। (2014)
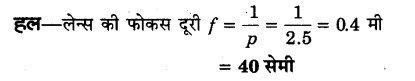
प्रश्न 17.
किसी उत्तल लेन्स की फोकस दूरी f, अपवर्तनांक n एवं लेन्स की वक्रता त्रिज्याओं R1 और R2 के बीच सम्बन्ध का सूत्र लिखिए। (2012)

प्रश्न 18.
एक उभयोत्तल लेन्स की दोनों वक्रता-त्रिज्याएँ 20 सेमी हैं तथा लेन्स के काँच का अपवर्तनांक 1.5 है। लेन्स की फोकस दूरी क्या होगी ? (2010)
उत्तर-
जब उभयोत्तल लेन्स की वक्रता त्रिज्याएँ समान होती हैं तब उसकी फोकस दूरी वक्रता त्रिज्या के समान होती है। अत: f = R = 20 सेमी।
प्रश्न 19.
यदि एक उत्तल लेन्स की वायु में फोकस दूरी 20 सेमी है, तो जल में उसकी फोकस दूरी क्या होगी ? (2010)
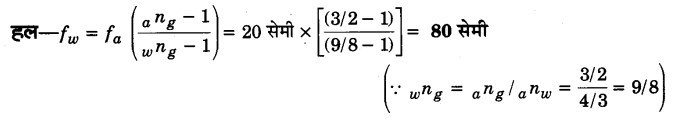
प्रश्न 20.
वायु के सापेक्ष काँच एवं जल का अपवर्तनांक क्रमशः एवं
है। जल के सापेक्ष काँच का अपवर्तनांक ज्ञात कीजिए।

प्रश्न 21.
एक पतले समतल-उत्तल लेन्स की फोकस दूरी 20.0 सेमी है। इस लेन्स के वक्र पृष्ठ की वक्रता त्रिज्या ज्ञात कीजिए। लेन्स के पदार्थ का अपवर्तनांक 1.5 है। (2013)
उत्तर-
R1 = ?, R2 = ∞, f = 20 सेमी तथा n = 1.5
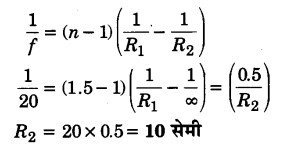
प्रश्न 22.
किस दशा में लेन्स की प्रथम फोकस दूरी का मान उसकी द्वितीय फोकस दूरी के मान के बराबर नहीं होता है? (2009, 10)
उत्तर-
जब लेन्स के दोनों ओर माध्यम भिन्न-भिन्न होता है।
प्रश्न 23.
20 सेमी फोकस दूरी वाले दो पतले उत्तल लेन्स सम्पर्क में रखे गये हैं। इससे 20 सेमी की दूरी पर रखी गयी वस्तु के लिए वस्तु एवं उसके प्रतिबिम्ब के बीच की दूरी ज्ञात कीजिए। (2015)

प्रश्न 24.
सम्पर्क में रखे दो पतले लेंसों के संयोजन की फोकस दूरी एवं क्षमता का सूत्र लिखिए। (2017)

प्रश्न 25.
दो उत्तल लेंस जिनमें प्रत्येक की फोकस दूरी 20 सेमी है सम्पर्क में रखे हैं। संयुक्त लेंस की क्षमता की गणना कीजिए। (2017)
हल-
दिया है, P1 = P2 = 20 सेमी
P = P1 + P2 = 20 + 20 = 40 सेमी
प्रश्न 26.
एक लेन्स जिसकी क्षमता +2D है -1D क्षमता वाले दूसरे लेन्स के साथ युग्म बनाता है। युग्म की तुल्य फोकस दूरी क्या होगी? (2017)
हल-
दिया है, P1 = + 2D, P2 = -1D
P = P1 + P2 = +2D + (-1D) = +1D
फोकस दूरी = =
= 100 सेमी
प्रश्न 27.
प्रिज्म के पदार्थ के अपवर्तनांक का सूत्र लिखिए। प्रयुक्त प्रतीकों का अर्थ बताइए। (2013, 14, 17)
या
किसी प्रिज्म के पदार्थ के अपवर्तनांक का सूत्र अल्पतम विचलन कोण एवं प्रिज्म कोण के पदों में व्यक्त कीजिए। (2013, 16)
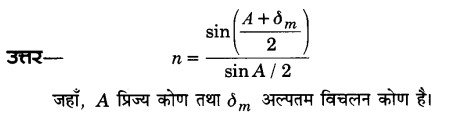
प्रश्न 28.
किसी प्रिज्म के लिये आपतन कोण तथा विचलन कोण के बीच का ग्राफ दिखाइए। विचलन कोण कब न्यूनतम होगा ? (2010, 12)
उत्तर-
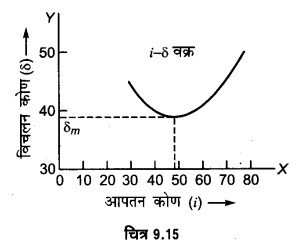
जब आपतन कोण तथा निर्गत कोण बराबर होते हैं, अर्थात् प्रिज्म के अन्दर अपवर्तित किरण प्रिज्म के आधार के समान्तर होती है; तब विचलन कोण न्यूनतम होगा।
प्रश्न 29.
किसी प्रकाशिक माध्यम की वर्ण विक्षेपण क्षमता का सूत्र लिखिए। (2014)

प्रश्न 30.
किसी पतले प्रिज्म द्वारा उत्पन्न न्यूनतम विचलन तथा कोणीय विक्षेपण के लिये सूत्र लिखिए। (2015, 17)
उत्तर-
न्यूनतम विचलन कोण δm = 2i – A
कोणीय विक्षेपण के लिए सूत्र θ = (nV – nR) A
जहाँ nV तथा nR क्रमशः लाल व बैंगनी रंगों के प्रकाश के लिए प्रिज्म के काँच के अपवर्तनांक हैं तथा A प्रिज्म का कोण है।
प्रश्न 31.
न्यूनतम विचलन की क्या सार्थकता है? (2010)
उत्तर-
न्यूनतम विचलन की सार्थकता- अल्पतम (न्यूनतम) विचलन की स्थिति में प्रिज्म के अन्दर अपवर्तित किरण प्रिज्म के आधार के समान्तर होती है तथा आपतन कोण व निर्गत कोण बराबर होते हैं।
प्रश्न 32.
किसी पदार्थ के लाल, बैंगनी तथा पीले रंग के प्रकाश के लिए अपवर्तनांक क्रमशः 1.52, 1.62 तथा 1.60 हैं। पदार्थ की वर्ण-विक्षेपण (परिक्षेपण) क्षमता ज्ञात कीजिए। (2011, 14)

प्रश्न 33.
लाल और नीले प्रकाश की किरणें एक दिये गये प्रिज्म पर डाली जाती हैं। किसके लिए अल्पतम विचलन कोण 6, का मान अधिक होगा? व्याख्या कीजिए। (2011)

प्रश्न 34.
काँच के एक प्रिज्म का कोण 60° है तथा अल्पतम विचलन कोण 39° है। काँच का अपवर्तनांक क्या है? दिया है, sin 49.5° = 0.76. (2012)

प्रश्न 35.
काँच से निर्मित एक पतले प्रिज्म से उत्पन्न न्यूनतम विचलन कोण 4° है। प्रिज्म कोण ज्ञात कीजिए। (काँच का अपवर्तनांक 1.5 है)। (2012)

प्रश्न 36.
एक पतले प्रिज्म का प्रिज्म कोण 4° है तथा इसके पदार्थ का अपवर्तनांक 1.5 है। प्रिज्म द्वारा उत्पन्न न्यूनतम विचलन कोण ज्ञात कीजिए। (2013)
हल-
δm = (n – 1) A = (1.5 – 1) 4° = 0.5 x 4° = 2°
प्रश्न 37.
न्यूनतम विचलन अवस्था में एक प्रकाश किरण एक समकोणिक प्रिज्म पर इस प्रकार आपतित होती है कि आपतन कोण, प्रिज्म कोण का है। न्यूनतम विचलन कोण ज्ञात कीजिए। (2014)
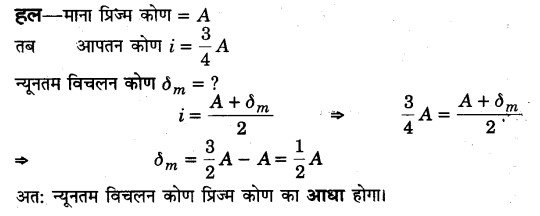
प्रश्न 38.
किसी पतले प्रिज्म से उत्पन्न न्यूनतम विचलन कोण 10° है। प्रिज्म कोण ज्ञात कीजिए। प्रिज्म के पदार्थ का अपवर्तनांक 1.5 है। (2016)

प्रश्न 39.
63° कोण वाले प्रिज्म का पीले प्रकाश के लिए विचलन कोण 29° है। आपतन कोण ज्ञात कीजिए। (2016)
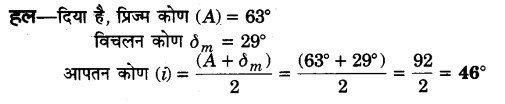
प्रश्न 40.
किसी प्रिज्म के पदार्थ की वर्ण विक्षेपण क्षमता से क्या तात्पर्य है? (2017)
उत्तर-
जब सूर्य का श्वेत प्रकाश एक पतले प्रिज्म में से गुजरता है, तो बैंगनी तथा लाल रंगों की निर्गत किरणों के बीच उत्पन्न कोणीय परिक्षेपण तथा मध्यवर्ती (अर्थात् पीले रंग की किरण के लिए विचलन कोण के अनुपात को प्रिज्म के पदार्थ की वर्ण विक्षेपण क्षमता कहते हैं। इसे ग्रीक अक्षर w (ओमेगा) से प्रदर्शित करते हैं।
प्रश्न 41.
फ्लिन्ट काँच के लिए बैंगनी एवं लाल रंगों के प्रकाश हेतु अपवर्तनांक क्रमशः 1.632 तथा 1.613 हैं। प्रिज्म के पदार्थ की विक्षेपण क्षमता की गणना कीजिए। (2017)

प्रश्न 42.
नेत्र की समंजन क्षमता से आप क्या समझते हैं ? (2017, 18)
उत्तर-
नेत्र की वह क्षमता जिसके कारण नेत्र लेन्स की फोकस दूरी में परिवर्तन कर नजदीक व दूर की वस्तुओं को स्पष्ट रूप से देखा जा सकता है, नेत्र की समंजन क्षमता कहलाती है।
प्रश्न 43.
एक व्यक्ति को पुस्तक पढ़ने के लिए पुस्तक को आँख से 35 सेमी दूर रखना पड़ता है। इस व्यक्ति के नेत्र में कौन-सा दोष है?
उत्तर-
दूर-दृष्टि दोष।
प्रश्न 44.
मनुष्य की आँख के रेटिना के कार्य का उल्लेख कीजिए। (2015)
उत्तर-
रेटिना प्रकाश- शिराओं की एक फिल्म होती है, जो वस्तुओं के प्रतिबिम्बों के रूप-रंग और आकार का ज्ञान मस्तिष्क तक पहुँचाती है। जिस स्थान पर प्रकाश-शिरा रेटिना को छेदकर मस्तिष्क में जाती है, उस स्थान पर प्रकाश का कोई प्रभाव नहीं पड़ता। इस स्थान को अंध-बिन्दु कहते हैं। रेटिना के बीचों-बीच एक पीत-बिन्दु होता है।
प्रश्न 45.
इलेक्ट्रॉन सूक्ष्मदर्शी, प्रकाशिक सूक्ष्मदर्शी से उत्तम क्यों माना जाता है? (2013)
उत्तर-
इलेक्ट्रॉन सूक्ष्मदर्शी, प्रकाशिक सूक्ष्मदर्शी की तुलना में किसी वस्तु का लगभग 5000 गुना आवर्धित प्रतिबिम्ब बनाता है, इसलिए यह प्रकाशिक सूक्ष्मदर्शी से उत्तम माना जाता है।
प्रश्न 46.
किसी प्रकाशिक यन्त्र की विभेदन क्षमता से क्या तात्पर्य है?
उत्तर-
किसी प्रकाशिक यन्त्र की दो पास-पास रखी वस्तुओं के प्रतिबिम्बों को अलग-अलग करने की क्षमता को विभेदन क्षमता (resolving power) कहते हैं।
प्रश्न 47.
आँख पर चन्द्रमा का दर्शन कोण 0.6° है। दूरदर्शी के अभिदृश्यक एवं नेत्रिका की फोकस दूरियाँ क्रमशः 200 सेमी एवं 10 सेमी हैं। दूरदर्शी से देखने पर चन्द्रमा का दर्शन कोण कितना होगा?

प्रश्न 48.
दूरदर्शी के अभिदृश्यक का द्वारक बड़ा क्यों बनाया जाता है? (2018)
उत्तर-
दूरदर्शी की विभेदन क्षमता तथा प्रतिबिम्ब की तीव्रता बढ़ाने के लिए इसके अभिदृश्यक का द्वारक बड़ा बनाया जाता है।
प्रश्न 49.
50 सेमी द्वारक के अभिदृश्यक लेन्स वाले दूरदर्शी की विभेदन सीमा कितनी होगी? अभिदृश्यक लेन्स में आपतित प्रकाश की तरंगदैर्घ्य λ = 6000 Å है।(2014)


प्रश्न 50.
सूक्ष्मदर्शी की विभेदन सीमा हेतु व्यंजक लिखिए। प्रयुक्त संकेतों के अर्थ लिखिए। (2015, 17)
उत्तर-
सूक्ष्मदर्शी की विभेदन सीमा =
जहाँ, λ = प्रकाश की तरंगदैर्घ्य,
μ = वस्तु एवं अभिदृश्यक लेन्स के बीच उपस्थित माध्यम का अपवर्तनांक,
θ = वस्तु एवं अभिदृश्यक के बीच बने प्रकाश शंकु का अर्द्धशीर्ष कोण।
प्रश्न 51.
परावर्ती दूरदर्शी में परवलयाकार दर्पण के द्वारक का मान अधिक क्यों रखा जाता है।
उत्तर-
जिससे दूरदर्शी में अधिक प्रकाश प्रवेश कर सके तथा प्रतिबिम्ब चमकीला बने।
प्रश्न 52.
-2D क्षमता वाले लेन्स का उपयोग करने वाले व्यक्ति को दूर बिन्दु कितनी दूरी पर होगा?

प्रश्न 53.
निकट दृष्टि दोष वाला व्यक्ति 15 सेमी दूर की वस्तु स्पष्ट देख सकता है। 25 सेमी दूर वस्तु को स्पष्ट देखने के लिए आवश्यक लेंस की फोकस दूरी निकालिए। (2017)

लघु उत्तरीय प्रश्न
प्रश्न 1.
प्रकाश के अपवर्तन से आप क्या समझते हैं? इसके नियम लिखिए।
उत्तर-
प्रकाश का अपवर्तन- जब प्रकाश एक पारदर्शी माध्यम से दूसरे पारदर्शी माध्यम में प्रवेश करता है, तो दूसरे माध्यम में जाने पर इसका वेग तथा दिशा बदल जाती है। इस घटना को प्रकाश का अपवर्तन कहते हैं।
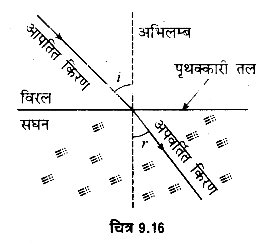
अपवर्तन के नियम-
प्रकाश का अपवर्तन निम्न दो नियमों के अनुसार होता है-
(i) आपतित किरण, अपवर्तित किरण और आपतन बिन्दु पर अभिलम्ब तीनों एक ही तल में होते हैं।
(ii) किन्हीं दो माध्यमों के लिए तथा एक निश्चित रंग (तरंगदैर्ध्य) के प्रकाश के लिए आपतन कोण की ज्या तथा अपवर्तन कोण की ज्या की निष्पत्ति एक नियतांक होती है। यदि आपतन कोण i व अपवर्तन कोण r हैं, तो
= नियतांक
इस नियम को स्नेल का नियम (Snell’s Law) कहते हैं तथा इस नियतांक को पहले माध्यम के सापेक्ष दूसरे माध्यम का अपवर्तनांक (refractive index) कहते हैं। यदि पहले व दूसरे माध्यम : को 1 व 2 से निरूपित करें, तो माध्यम 2 का 1 के सापेक्ष अपवर्तनांक 17 से प्रदर्शित करते हैं।
इस प्रकार
=
किसी पदार्थ का अपवर्तनांक (i) माध्यम की प्रकृति, (ii) माध्यम की भौतिक अवस्था, (iii) प्रकाश के रंग तथा (iv) माध्यम के ताप पर निर्भर करता है।
प्रश्न 2.
किसी अवतल दर्पण के लिए सूत्र की स्थापना कीजिए, जहाँ संकेतों के सामान्य अर्थ हैं। (2017)
हल-
माना कि M1 M2 एक अवतल दर्पण है जिसका ध्रुव P है, फोकस F है तथा व्रकता केन्द्र C है (चित्र 9.17)। इसकी मुख्य अक्ष के किसी बिन्दु पर एक वस्तु AB रखी है। वस्तु के सिरे A से मुख्य अक्ष के समानान्तर चलने वाली आपतित किरण AM दर्पण के बिन्दु M से टकराती है। परावर्तन के पश्चात् यह किरण दर्पण के फोकस F से होकर गुजरती है। दूसरी किरण AO दर्पण के वक्रता केन्द्र से होकर जाती है तथा परावर्तन के पश्चात् उसी मार्ग से वापस लौट जाती है। दोनों परावर्तित किरणें बिन्दु A’ पर काटती हैं। इस बिन्दु A’ से मुख्य अक्ष पर डाला गया लम्ब A’ B’, वस्तु AB की प्रतिबिम्ब है। अब, माना कि वस्तु AB की दर्पण के ध्रुव से दूरी PB = -u, प्रतिबिम्ब A’B’ की दूरी PB’ = -v, दर्पण की वक्रता त्रिज्या PC = -R तथा दर्पण की फोकस दूरी PF = -f है। (ये सभी दूरियाँ चूंकि आपतित किरण के चलने की दिशा के विपरीत दिशा में नापी जाती हैं अर्थात् दर्पण के बायीं ओर हैं; अत: चिह्न परिपाटी के अनुसार ये दूरियाँ ऋणात्मक हैं।)
ΔABC तथा ΔA’B’C समकोणिक हैं।



प्रश्न 3.
परस्पर सम्पर्क में रखे दो पतले लेन्सों के संयोजन की फोकस दूरी के लिए सूत्र की स्थापना कीजिए। (2011, 15, 16, 17)
या
परस्पर सम्पर्क में रखे दो पतले उत्तल लेन्सों के संयोजन की फोकस दूरी F के लिए सूत्र की स्थापना कीजिए, जहाँ f1 तथा f2 क्रमशः दोनों लेन्सों की फोकस दूरियाँ हैं।
या
f1 फोकस दूरी को उत्तल लेन्स f2 फोकस दूरी के अवतल लेन्स के सम्पर्क में रखा है। संयुक्त लेन्स की फोकस दूरी एवं प्रकृति ज्ञात कीजिए, जबकि f1 < f2.
उत्तर-
चित्र 9.18 के अनुसार दो पतले उत्तल लेन्सों L1 व L2 को सम्पर्क में रखकर एक संयुक्त लेन्स बनाया गया है। माना इनकी फोकस दूरियाँ क्रमशः f1 व f2 हैं तथा इस संयुक्त लेन्स द्वारा बिन्दु-वस्तु O का प्रतिबिम्ब I पर बनता है। प्रतिबिम्ब बनने की प्रक्रिया को निम्न प्रकार समझा जा सकता है-
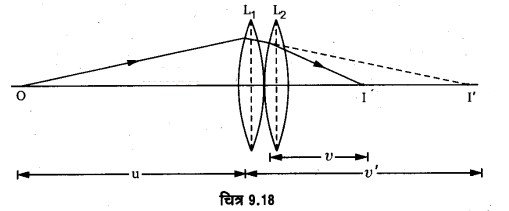
यदि L2 लेन्स न हो तो वस्तु O का प्रतिबिम्ब लेन्स L1 द्वारा I’ पर बनता। यदि I’ की L1 से दूरी v’ हो तथा L1 से O की दूरी u हो, तो लेन्स के सूत्र से

अब, प्रतिबिम्ब I’ लेन्स L2 के लिए आभासी वस्तु का कार्य करता है जो इसका प्रतिबिम्ब I पर बनाता है। प्रतिबिम्ब I की L2 से दूरी । हो, तो लेन्स के सूत्र से,

समी० (1) व समी० (2) को जोड़ने पर

यदि इन दोनों लेन्सों के स्थान पर एक ऐसे पतले लेन्स का प्रयोग करें जो u दूरी पर रखी वस्तु का प्रतिबिम्ब v दूरी पर बनाये, तो लेन्स की फोकस दूरी F के लिए।

समी० (3) व समी० (4) की तुलना करने पर

इस सूत्रे से संयुक्त लेन्स की फोकस दूरी की गणना की जा सकती है।
समीकरण (5) प्राप्त करने के लिए दो उत्तल लेन्सों को सम्पर्क में रखा हुआ माना गया है, परन्तु यह समीकरण ऐसे संयुक्त लेन्स के लिए भी सही है जो एक उत्तल एवं एक अवतल लेन्स से बना हो, अथवा दो अवतल लेन्सों से बना हो। समीकरण (5) का उपयोग करते समय इस बात को ध्यान में रखते हैं कि उत्तल लेन्स के लिए फोकस दूरी धनात्मक एवं अवतल लेन्स की फोकस दूरी ऋणात्मक लेते हैं। यदि L1 उत्तल लेन्स एवं L2 अवतल लेन्स हो, तो

- यदि f1 > f2, तब F ऋणात्मक होगा और संयुक्त लेन्स अवतल लेन्स की भाँति कार्य करेगा।
- यदि f1 < f2, तब F धनात्मक होगा और संयुक्त लेन्स उत्तल लेन्स की भाँति कार्य करेगा।
- यदि f1 = f2, तब F अनन्त होगा और संयुक्त लेन्स समतल प्लेट की भाँति कार्य करेगा।
प्रश्न 4.
एक लेन्स जिसकी फोकस दूरी f है, एक दीप्त वस्तु का चित्र पर्दे पर m गुना बड़ा बनाता है। सिद्ध कीजिए कि पर्दे की लेन्स से दूरी (m + 1) f है। (2011, 13)
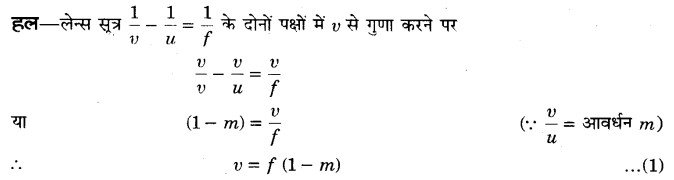
परन्तु पर्दे पर प्राप्त चित्र वास्तविक होता है जिसके लिए m ऋणात्मक होता है।
अत: समी० (1) में .m के स्थान पर (-m) रखने पर पर्दे की लेन्स से दूरी v = f (1 + m) = (m + 1) f.
प्रश्न 5.
एक उत्तल लेन्स 20 सेमी फोकस दूरी का तथा एक अवतल लेन्स 25 सेमी फोकस दूरी का, सम्पर्क में रखे गये हैं। इस युग्म से 2 मी दूरी पर रखी वस्तु के प्रतिबिम्ब की स्थिति तथा प्रकृति ज्ञात कीजिए। (2013)
हल-
प्रश्नानुसार, उत्तल लेन्स की फोकस-दूरी f1 = +20 सेमी तथा अवतल लेन्स की फोकस-दूरी f2 = -25 सेमी। यदि इन लेसों को परस्पर सम्पर्क में रखने पर बने लेन्स युग्म की फोकस-दूरी F हो, तो

परन्तु प्रतिबिम्ब के आकार तथा वस्तु के आकार का अनुपात आवर्धन (m) होता है। अतः प्रतिबिम्ब का आकार वस्तु के आकार के बराबर होगा। आवर्धन (m) का ऋणात्मक चिह्न इस बात का प्रतीक है कि प्रतिबिम्ब उल्टा बनेगा। इस प्रकार प्रतिबिम्ब युग्म से 2 मीटर दूरी पर वस्तु की दिशा की विपरीत दिशा में अर्थात् युग्म के पीछे उल्टा, वास्तविक तथा आकार में वस्तु के बराबर बनेगा।
प्रश्न 6.
दो पतले लेन्स सम्पर्क में रखे हैं। एक लेन्स की फोकस दूरी 30.0 सेमी है। यदि संयोजन की फोकस दूरी 15.0 सेमी हो, तो दूसरे लेन्स की फोकस दूरी ज्ञात कीजिए। यदि एकसमान फोकस दूरी के विपरीत प्रकृति वाले दो लेन्सों को सम्पर्क में रखा जाए, तो संयोजन की. क्षमता क्या होगी? (2015)

एकसमान फोकस दूरी एवं विपरीत प्रकृति वाले दो लेन्सों को सम्पर्क में रखने पर, संयोजन की फोकस दूरी अनन्त होगी।
अतः संयोजन की क्षमता शून्य होगी।
प्रश्न 7.
एक उभयोत्तल लेन्स 1.5 अपवर्तनांक के काँच से बना है। इसके दोनों पृष्ठों की वक्रता त्रिज्याएँ 20 सेमी हैं। लेन्स की क्षमताओं का अनुपात ज्ञात कीजिए जब इसे हवा में रखा जाए और जब इसे 1.25 अपवर्तनांक के द्रव में डुबाया जाए। (2014)
हल-
वायु के लिए लेन्स की क्षमता

प्रश्न 8.
एक वस्तु से पर्दा 75 सेमी की दूरी पर है। इनके बीच में 12 सेमी फोकस दूरी वाले उत्तल लेन्स को कहाँ रखा जाए, जिससे पर्दे पर वस्तु का वास्तविक प्रतिबिम्ब बन जाए। (2016)
हल-
दिया है, u = 75 सेमी, f = 12 सेमी

अतः उत्तल लेन्स को 10.3 सेमी की दूरी पर रखा जाएगा।
प्रश्न 9.
एक 10 सेमी वक्रता त्रिज्या वाले काँच (ng = ) के द्वि-उत्तल लेन्स AB को तल के अनुदिश दो बराबर भागों में काटा जाता है। लेन्स के किसी एक भाग (nω =
) में डुबाने पर उस भाग की फोकस दूरी की गणना कीजिए। (2017)
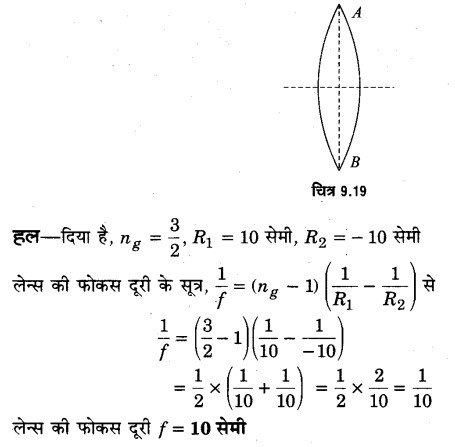
प्रश्न 10.
प्रकाश के दो बिन्दु स्रोतों के बीच की दूरी 30 सेमी है। एक स्रोत से 20 सेमी दूर एक उत्तल लेन्स रखने पर दोनों स्रोतों के प्रतिबिम्ब एक ही बिन्दु पर बनते हैं। उसे उत्तल लेन्स की फोकस दूरी ज्ञात कीजिए तथा संगत किरण आरेख भी बनाइए। (2017)
उत्तर-
चित्रानुसार, O1 व O2 दो प्रकाश स्रोत हैं जिनके बीच की दूरी 30 सेमी है। लेन्स, स्रोत O1 से 20 सेमी की दूरी पर रखा है तथा O2 का (वास्तविक) प्रतिबिम्ब I बनाता है। स्रोत O2 से लेन्स की दूरी 10 सेमी है तथा प्रश्नानुसार O2 का आभासी प्रतिबिम्ब भी 1 पर ही बनता है।
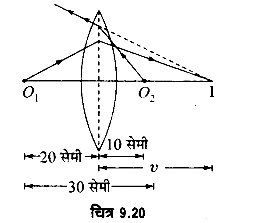
प्रश्नानुसार, दोनों वस्तुओं के प्रतिबिम्ब एक ही बिन्दु पर (लेन्स के एक ही ओर) बनते हैं, अत: इनमें से एक वास्तविक तथा दूसरा आभासी होगा अर्थात् लेन्स के समीप वाली वस्तु फोकस से पहले रखी होगी।
स्रोत O1 के लिए, u = -20 सेमी


प्रश्न 11.
प्रकाश के वर्ण-विक्षेपण से आप क्या समझते हैं? एक प्रिज्म द्वारा श्वेत प्रकाश का वर्णविक्षेपण किस प्रकार होता है? समझाइए।
उत्तर-
श्वेत प्रकाश विभिन्न रंगों के प्रकाश का मिश्रण होता है। जब श्वेत प्रकाश की किरण प्रिज्म पर आपतित होती है तो विभिन्न रंगों की अनेक किरणों में विभाजित हो जाती है। इस प्रक्रिया को प्रकाश को ‘वर्ण-विक्षेपण’ (dispersion) कहते हैं। वर्ण-विक्षेपण का कारण किसी पदार्थिक माध्यमं में भिन्न-भिन्न रंगों में प्रकाश की चाल का भिन्न-भिन्न होना है। अत: किसी पदार्थ का अपवर्तनांक n भिन्न-भिन्न रंगों में प्रकाश के लिए भिन्न-भिन्न होता है। काँच का अपवर्तनांक बैंगनी प्रकाश के लिए सबसे अधिक होता है। अत: सूत्र δm = (n – 1) A के अनुसार, बैंगनी प्रकाश का विचलन कोण लाल प्रकाश के विचलन कोण से बड़ा होता है। भिन्न-भिन्न रंगों के लिए भिन्न-भिन्न विचलन कोण होने के कारण, श्वेत प्रकाश के प्रिज्म में प्रवेश करने पर इसमें से भिन्न रंगों की किरणें भिन्न-भिन्न दिशाओं में निकलती हैं। बैंगनी रंग के प्रकाश की किरण प्रिज्म के आधार की ओर सबसे अधिक तथा लाल प्रकाश की ओर सबसे कम झुकती है। अत: श्वेत प्रकाश विभिन्न रंगों की किरणों में विभाजित हो जाता है। इसी को वर्ण-विक्षेपण कहते हैं।
प्रश्न 12.
काँच () पतले प्रिज्म द्वारा प्रकाश किरण का अल्पतम विचलन कोण 60° है। यदि पप्रिज्म को जल (
) में डुबो देया जाए तो विचलन कोण कितना हो जायेगा? (2012)

प्रश्न 13.
एक पतले प्रिज्म के पदार्थ के लिए लाल एवं बैंगनी रंगों के अपवर्तनांक 1.65 हैं। पदार्थ की विक्षेपण क्षमता 0.08 है। प्रकाश के पीले रंग के लिए प्रिज्म का विचलन कोण 5.0° है। प्रिज्म कोण की गणना कीजिए। (2011)

प्रश्न 14.
किसी प्रिज्म के पदार्थ के लिए लाल, बैंगनी, पीले रंग के प्रकाश के अपवर्तनांक क्रमशः 1.51, 1.61 तथा 1.59 हैं। पदार्थ की वर्ण-विक्षेपण क्षमता ज्ञात कीजिए। यदि माध्य विचलन 5° हो, तो कोणीय वर्ण-विक्षेपण कितना होगा? (2012)

प्रश्न 15.
किसी प्रिज्म से अल्पतम-विचलन कोण 30°, प्रिज्म के प्रथम अपवर्तक पृष्ठ पर अपवर्तन कोण 30° है। प्रिज्म के पदार्थ का अपवर्तनांक ज्ञात कीजिए। (2011, 16)

प्रश्न 16.
A प्रिज्म कोण वाले प्रिज्म के पदार्थ का अपवर्तनांक Cosec () है। न्यूनतम विचलन कोण का मान ज्ञात कीजिए। (2014)

प्रश्न 17.
प्रकाश का प्रकीर्णन क्या है? प्रकीर्णन पर आधारित रमन प्रभाव क्या है? (2016, 18)
हल-
प्रकाश का प्रकीर्णन- माध्यम के कणों द्वारा प्रकाश ऊर्जा को अवशोषित कर अन्य दिशाओं में पुनः विकरित करने की क्रिया को प्रकाश का प्रकीर्णन कहते हैं। बेन्जीन जैसे कार्बनिक द्रव पर प्रकाश के तीव्र किरण पुंज को डालकर उससे प्रकीर्णित प्रकाश का अध्ययन करते हुए देखा कि प्रकीर्णित प्रकाश में आपतित प्रकाश की आवृत्ति v की रेखा के अतिरिक्त उससे कम आवृत्ति (v – v1) (v – v2)… तथा उससे अधिक आवृत्ति (v + v1) (v + v2) …. की भी रेखाएँ प्राप्त होती हैं, जिन्हें स्टोक रेखाएँ तथा प्रतिस्टोक रेखाएँ कहते हैं। इस स्पेक्ट्रम को रमन स्पेक्ट्रम तथा इस प्रभाव को रमन प्रभाव कहते हैं।
प्रश्न 18.
फ्लिण्ट काँच के लिए बैंगनी, पीले तथा लाल रंगों के प्रकाश के लिए अपवर्तनांक क्रमशः 1.632, 1.620 तथा 1.613 है। फ्लिट काँच के पदार्थ की विक्षेपण क्षमता ज्ञात कीजिए। (2016)
हल-
फ्लिण्ट काँच के पदार्थ की विक्षेपण क्षमता

प्रश्न 19.
(a) 25.0 सेमी तथा 2.5 सेमी फोकस दूरी वाले दो उत्तल लेन्स दिए गए हैं। दूरदर्शी बनाने हेतु इनको किस प्रकार समायोजित करेंगे? एक स्वच्छ चित्र द्वारा प्रतिबिम्ब के बनने को प्रदर्शित कीजिए। इस दूरदर्शी की आवर्धन क्षमता कितनी होगी?
(b) खगोलीय दूरदर्शक के अभिदृश्यक तथा नेत्रिका की फोकस दूरियाँ क्रमशः 250 सेमी व 10 सेमी हैं। अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की (i) न्यूनतम दूरी पर बनता है, (ii) अनन्तता पर बनता है। दोनों दशाओं में दूरदर्शक की आवर्धक क्षमता की गणना कीजिए। (2015)
हल-
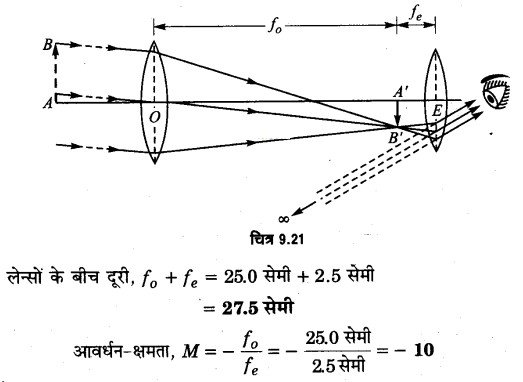
(a) 25.0 सेमी फोकस दूरी वाला उत्तल लेन्स अभिदृश्यक O, तथा 2.5 सेमी वाला नेत्रिका E के रूप में प्रयुक्त किया जायेगा। श्रांत आँख (relaxed eye) से देखने के लिए अन्तिम प्रतिबिम्ब अनन्तता पर बनना चाहिए। इसके लिए नेत्रिका E तथा अभिदृश्यक O के बीच दूरी इतनी रखते हैं कि दूर-स्थित वस्तु AB का अभिदृश्यक द्वारा बना प्रतिबिम्ब A’B’, नेत्रिका E के फोकस पर पड़े (चित्र 9.21)। स्पष्ट है कि इसके लिए दोनों लेन्सों के बीच दूरी (f0 + fe) के बराबर होगी, जहाँ f0 अभिदृश्यक की तथा fe नेत्रिका की फोकस दूरी है।

प्रश्न 20.
सूक्ष्मदर्शी की विभेदन-क्षमता से आप क्या समझते हैं? इसका सूत्र लिखिए तथा बताइए कि यह किस प्रकार बढ़ाई जा सकती है? या किसी सूक्ष्मदर्शी की विभेदन-क्षमता से क्या तात्पर्य है? (2013)
या
सूक्ष्मदर्शी की विभेदन-क्षमता के लिए व्यंजक लिखिए। सूक्ष्मदर्शी की विभेदन क्षमता कैसे बढ़ायी जा सकती है? (2015)
उत्तर-
किसी सूक्ष्मदर्शी की विभेदन- क्षमता उसकी दो समीपवर्ती वस्तुओं के प्रतिबिम्बों को अलग-अलग करने की क्षमता है। सूक्ष्मदर्शी की विभेदन-क्षमता प्रयुक्त प्रकाश की तरंगदैर्घ्य (λ) के व्युत्क्रमानुपाती तथा सूक्ष्मदर्शी में प्रवेश करने वाली प्रकाश-किरणों के शंकु-कोण के अनुक्रमानुपाती होती है।

जहाँ λ प्रकाश की तरंगदैर्घ्य है, n वस्तु तथा अभिदृश्यक के बीच माध्यम का निरपेक्ष अपवर्तनांक तथा α = अर्द्ध शंकु-कोण।
सूक्ष्मदर्शी का उपयोग समीप की वस्तुओं को देखने में होता है; जैसे—सूक्ष्म कण, स्लाइडे इत्यादि। इन वस्तुओं को किसी प्रकाश-स्रोत से प्रकाशित करते हैं। इसकी विभेदन-सीमा घटाने के लिए (अथवा विभेदन-क्षमता बढ़ाने के लिए) शंकु-कोण का मान अधिक नहीं बढ़ाया जा सकता है, परन्तु छोटे तरंगदैर्घ्य के प्रकाश का प्रयोग करके λ का मान घटाया जा सकता है। अतः साधारण प्रकाश के स्थान पर नीला प्रकाश प्रयुक्त करके सूक्ष्मदर्शी की विभेदन-क्षमता को बढ़ाया जा सकता है।
प्रश्न 21.
किसी दूरदर्शी की विभेदन-क्षमता से क्या तात्पर्य है? इसका सूत्र लिखिए। दूरदर्शी की विभेदन-क्षमता कैसे बढ़ायी जाती है? (2017)
या
दूरदर्शी की विभेदन-क्षमता का सूत्र लिखिए तथा प्रयुक्त संकेतों के अर्थ लिखिए। यह किन-किन बातों पर निर्भर करती है? (2009)
या
दूरदर्शी की विभेदन क्षमता का सूत्र लिखिए तथा प्रयुक्त प्रतीकों के अर्थ बताइए। इसको . कैसे बढ़ाया जा सकता है? (2011, 12)
उत्तर-
दो समीपवर्ती वस्तुओं को दूरदर्शी द्वारा देखने पर प्रतिबिम्बों को अलग-अलग करने की क्षमता को दूरदर्शी. की ‘विभेदन-क्षमता’ कहते हैं।

स्पष्ट है कि दूरदर्शी की विभेदन-क्षमता, दूरदर्शी के अभिदृश्यक लेन्से का व्यास (d) बढ़ाकर बढ़ायी जा सकती है अर्थात्, विभेदन-क्षमता अभिदृश्यक के द्वारक तथा प्रकाश की तरंगदैर्ध्य पर निर्भर करती है।
प्रश्न 22.
संयुक्त सूक्ष्मदर्शी का नामांकित किरण आरेख बनाइए जब अन्तिम प्रतिबिम्ब अनन्तता पर बनता है। इसकी विभेदन क्षमता कैसे बढ़ायी जा सकती है? (2015)
उत्तर-
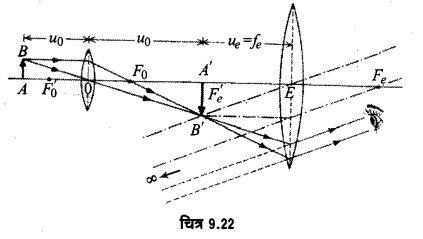
श्रांत आँख के लिए अन्तिम प्रतिबिम्ब A”B” अनन्तता पर बनता है। इस दशा में प्रतिबिम्ब A’B’, नेत्रिका E के फोकस F’e पर होगा। संयुक्त सूक्ष्मदर्शी की विभेदन क्षमता के लिए उपर्युक्त प्रश्न (20) देखिए।
प्रश्न 23.
इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन-क्षमता प्रकाशीय इलेक्ट्रॉन सूक्ष्मदर्शी की तुलना में अधिक क्यों होती है? (2011, 13)
या
इलेक्ट्रॉन सूक्ष्मदर्शी की उपयोगिता बताइए। (2010)
या
समझाइए कि किसी इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन क्षमता, प्रकाश सूक्ष्मदर्शी से अधिक क्यों होती है? (2013)
उत्तर-
इलेक्ट्रॉन सूक्ष्मदर्शी- आजकल अतिसूक्ष्म वस्तुओं के चित्र लेने के लिए इलेक्ट्रॉन सूक्ष्मदर्शी (electron microscope) काम में लाया जाता है। इसमें प्रकाश पुंज के स्थान पर तीव्रगामी इलेक्ट्रॉन पुंज को प्रयुक्त करते हैं। इलेक्ट्रॉन पुंज तरंग की तरह व्यवहार करता है जिसकी तरंगदैर्घ्य डी-ब्रॉगली के सिद्धान्तानुसार λ = (h/mυ) बहुत छोटी अर्थात् 1 Å की कोटि (order) की होती है। यह दृश्य प्रकाश की तरंगदैर्ध्य से लगभग 5000 गुना छोटी होती है। परन्तु विभेदन-क्षमता तरंगदैर्घ्य के व्युत्क्रमानुपाती होती है। अतः इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन-क्षमता, प्रकाशिक सूक्ष्मदर्शी की तुलना में लगभग 5000 गुना अधिक होती है। यही इस सूक्ष्मदर्शी की उपयोगिता है।
प्रश्न 24.
एक दूर-दृष्टि दोष वाले मनुष्य का निकट बिन्दु आँख से 150 सेमी पर है। यदि वह 25 सेमी दूर स्थित पुस्तक को पढ़ना चाहता है तो उसे कैसा तथा कितनी फोकस दूरी का लेन्स लगाना होगा? (2014, 17)
हल-
इस व्यक्ति की आँख का निकट-बिन्दु 150 सेमी पर है। उसे एक ऐसा लेन्स चाहिए जो 25 सेमी की दूरी पर स्थित वस्तु का प्रतिबिम्ब 150 सेमी पर बना दे। इस प्रकार लेन्स के लिए u = -25 सेमी तथा v = -150 सेमी

प्रश्न 25.
एक निकट दृष्टि दोष वाला व्यक्ति 30 सेमी से अधिक दूर की वस्तु को स्पष्ट नहीं देख सकता है। अनन्त पर स्थित वस्तु को देखने के लिए कितनी फोकस दूरी के तथा किस प्रकार के लेन्स की आवश्यकता होगी? (2016)
हल-
दिया है, u = -∞, v = -30 सेमी, f = ?

अत: व्यक्ति को अनन्त पर स्थित वस्तु को देखने के लिए 30 सेमी फोकस-दूरी के अवतल लेन्स की आवश्यकता होगी।
प्रश्न 26.
दूरदृष्टि दोष वाले व्यक्ति का निकट बिन्दु आँख से 100 सेमी है। आँख से 25 सेमी की दूरी पर रखी किताब को स्पष्ट पढने के लिए कितनी क्षमता का लेन्स आवश्यक है? इसके लिए किस प्रकार के लेन्स का प्रयोग किया जाएगा? (2017)

प्रश्न 27.
एक दूरदर्शी में अभिदृश्यक एवं नेत्रिका की फोकस दूरियाँ क्रमशः 100 सेमी और 50 सेमी हैं। दूरदर्शी की अधिकतम लम्बाई और आवर्धन क्षमता की गणना कीजिए। (2017)

दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
क्रान्तिक कोण तथा पूर्ण आन्तरिक परावर्तन से क्या अभिप्राय है ? सिद्ध कीजिए कि , जहाँ संकेतों के सामान्य अर्थ हैं।
या
सिद्ध कीजिए कि सघन माध्यम का अपवर्तनांक क्रान्तिक कोण की ज्या (sine) का व्युत्क्रमानुपाती होगा। (2015, 17)
या
पूर्ण आन्तरिक परावर्तन की व्याख्या कीजिए तथा क्रान्तिक कोण के महत्त्व को रेखांकित कीजिए। (2015)
या
पूर्ण आन्तरिक परावर्तन से आप क्या समझते हैं? इसकी आवश्यक शर्ते लिखिए। (2015)
उत्तर-
जब कोई प्रकाश-किरण सघन माध्यम से विरल माध्यम में प्रवेश करती है तो इसका अधिकांश भाग अपवर्तित हो जाता है तथा शेष भाग परावर्तित हो जाता है। इस दशा में प्रकाश-किरण अभिलम्ब से दूर हटती है, अत: अपवर्तन कोण का मान आपतन कोण से बड़ा होता है।
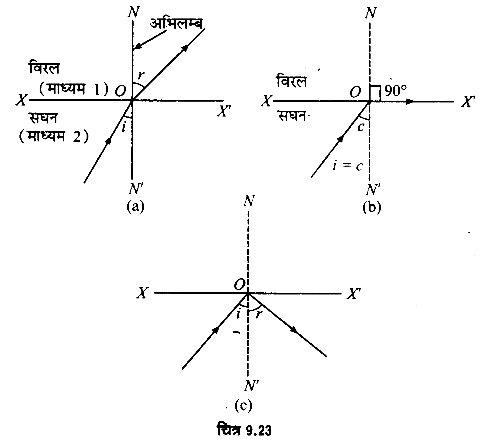
अब यदि सघने माध्यम में आपतन कोण (i) को बढ़ाते जायें तो विरल माध्यम में अपवर्तन कोण (r) का मान भी बढ़ता जाता है। एक विशेष आपतन कोण के लिए अपवर्तन कोण 90° हो जाता है। इस आपतन कोण को ‘क्रान्तिक कोण’ कहा जाता है तथा ‘C’ से प्रदर्शित करते हैं। अतः क्रान्तिक कोण को निम्न प्रकारे से परिभाषित किया जाता है-
“सघन माध्यम में बना वह आपतन कोण जिसके लिए विरले माध्यम में बना अपवर्तन कोण समकोण अर्थात् 90° होता है, दोनों माध्यमों के अन्तरापृष्ठ के लिए क्रान्तिक कोण कहलाता है।”
जब यदि माध्यम में आपतन कोण का मान क्रान्तिक कोण से आगे थोड़ा-सा ही बढ़ाया जाता है, तो सम्पूर्ण आपतित प्रकाश, परावर्तन के नियमों के अनुसार परावर्तित होकर सघन माध्यम में ही वापस लौट आता है। इस घटना को प्रकाश का पूर्ण आन्तरिक परावर्तन कहते हैं। अतः पूर्ण आन्तरिक परावर्तन की घटना होने के लिए अग्रलिखित शर्तों का पूरा होना आवश्यक है-
- प्रकाश सघनं माध्यम से विरल माध्यम में जाना चाहिए।
- सघन माध्यम में आपतन कोण का मान क्रान्तिक कोण से बड़ा होना चाहिए।
अपवर्तनांक तथा क्रान्तिक कोण में सम्बन्ध- यदि विरल माध्यम को माध्यम -1 तथा सघन माध्यम को माध्यम -2 से प्रदर्शित करें तो स्नेल के नियम के अनुसार,

इस प्रकार क्रान्तिक कोण की ज्या (sin) को व्युत्क्रम विरल माध्यम के सापेक्ष सघन माध्यम के अपवर्तनांक के बराबर होता है।
प्रश्न 2.
प्रकाशिक तन्तु क्या होते हैं? इनकी रचना, कार्य सिद्धान्त तथा अनुप्रयोग लिखिए। इसमें किस घटना का उपयोग होता है? (2015)
या
प्रकाशिक तन्तु नलिका में पूर्ण आन्तरिक परावर्तन की प्रक्रिया चित्र द्वारा समझाइए तथा आवश्यक सूत्र भी लिखिए। (2018)
उत्तर-
प्रकाशिक तन्तु- प्रकाशिक तन्तु पूर्ण आन्तरिक परावर्तन की घटना पर आधारित वह युक्ति है। जिसकी सहायता से एक प्रकाश सिग्नल को एक स्थान से दूसरे स्थान तक बिना ऊर्जा-ह्रास के प्रक्षेपित किया जा सकता है। रचना-इसको चित्र 9.24 में दर्शाया गया है। यह उच्च कोटि के काँच (क्वार्ट्ज अपवर्तनांक 1.7) के अत्यधिक लम्बे तथा पतले हजारों तन्तुओं (fibers) से मिलकर बना होता है। प्रत्येक रेशे (तन्तु) की मोटाई लगभग माइक्रो मीटर (10-6 मी) कोटि की होती है। तन्तु (क्वार्ट्ज के रेशे के चारों ओर अपेक्षाकृत कम अपवर्तनांक (n = 1.5) वाले पदार्थ की पतली तह लेपित कर दी जाती है। पाइप के भीतरी भाग को क्रोड (core) तथा लेपित भाग को अधिपट्टन (cladding) कहते हैं। क्रोड के पदार्थ का अपवर्तनांक अधिपट्टन के अपवर्तनांक की तुलना में अधिक होता है।
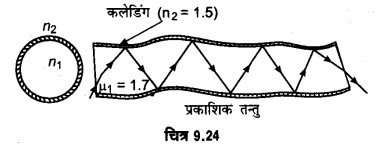
इस प्रकार के पाइपों की बड़ी संख्या के समूह को एक पाइप में डाल दिया जाता है जिसे प्रकाश पाइप (light pipe) कहते हैं तथा इसे प्रकाश सिग्नलों के प्रेक्षण में प्रयुक्त किया जाता है।
कार्य सिद्धान्त- जब प्रकाश किरण तन्तु के एक सिरे पर अल्प कोण बनाती हुई आपतित होती है तो यह इसके अन्दर अपवर्तित होकर तन्तु तथा तन्तु के ऊपर किये गये लेप के अन्तरापृष्ठ पर क्रान्तिक कोण से बड़े कोण पर आपतित होती है। अतः यह किरण यहाँ से पूर्ण परावर्तित होकर इसके सम्मुख वाले अन्तरापृष्ठ पर टकराती है। यहाँ पर यह पुनः क्रान्तिक कोण से बड़े कोण पर आपतित होती है। इसलिए यह पुनः पूर्ण आन्तरिक परावर्तित हो जाती है। इस प्रकार यह किरण बार-बार पूर्ण आन्तरिक परावर्तित होती हुई प्रकाशिक तन्तु के दूसरे सिरे पर पहुँच जाती है। तन्तु के इस सिरे पर यह किरण वायु में अपवर्तित होकर अभिलम्ब से दूर हटती हुई तीव्रता के कम हुए बिना बाहर निकल जाती है।
अनुप्रयोग- इनके अनुप्रयोग निम्नलिखित हैं-
1. संचार प्रणाली में प्रकाशिक तन्तु से संदेशों को मॉडुलन (modulation) द्वारा एक साथ एक स्थान से दूसरे स्थान तक भेजा जा सकता है। संदेशों की अधिक संख्या उच्च आवृत्ति वाली वैद्युत-चुम्बकीय तरंगों द्वारा मॉडुलित करके एक साथ संचारित की जा सकती है। प्रकाश अति उच्च आवृत्ति वाली वैद्युत-चुम्बकीय तरंग है। इनका संचरण सुचालक तार के स्थान पर प्रकाशिक तन्तु द्वारा किया जा सकता है। आधुनिक युग में प्रकाशिक तन्तुओं का उपयोग टेलीफोन व संचार लाइनों के रूप में हो रहा है।
2. प्रकाशीय तन्तु विद्युत संकेतों को एक स्थान से दूसरे स्थान तक संचरित करने में काम आते हैं। ये विद्युत संकेत परांतरित्र (transducer) द्वारा प्रकाश में परिवर्तित कर दिये जाते हैं। अब इन प्रकाशीय संकेतों को प्रकाश तन्तुओं द्वारा दूरस्थ स्थानों तक भेज दिया जाता है।
3. प्रकाशीय तन्तुओं द्वारा वस्तुओं के प्रतिबिम्बों को दूरस्थ स्थानों पर भेजा जा सकता है।
4. इनका प्रयोग सजावट करने वाले लैम्पों में किया जाता है। फव्वारों में जल की धारा को प्रकाशित करने में इनका प्रयोग किया जाता है।
प्रश्न 3.
किसी गोलीय पृष्ठ पर अपवर्तन का सूत्र, प्रयुक्त चिह्नों का अर्थ बताते हुए लिखिए तथा इसकी सहायता से पतले लेन्स के लिए सम्बन्ध सिद्ध कीजिए। (2009, 15)
या
किसी लेन्स की फोकस दूरी के लिये उसके दोनों पृष्ठों की वक्रता त्रिज्याओं तथा उसके पदार्थ के अपवर्तनांक के पदों में एक व्यंजक का निगमन कीजिए। यदि काँच के लेन्स को ऐसे व्रव में डुबा दिया जाये जिसका अपवर्तनांक काँच के अपवर्तनांक से अधिक हो, तो इसकी फोकस दूरी में क्या परिवर्तन हो जाएगा? (2010)
या
किसी गोलीय पृष्ठ पर प्रकाश के अपवर्तन का सूत्र लिखिए। इसकी सहायता से किसी पतले लेन्स की फोकस दूरी के लिए सूत्र स्थापित कीजिए। (2012, 14, 16, 17)
या
यदि एक लेन्स के दोनों ओर माध्यम एक ही हो, तो पतले लेन्स की फोकस दूरी के लिए अपवर्तनांक और वक्रता त्रिज्याओं के पदों में सूत्र व्युत्पन्न कीजिए। यदि एक काँच लेन्स, काँच की अपेक्षा अधिक अपवर्तनांक के एक द्रव में डुबोया जाये तो इसकी फोकस दूरी एवं प्रकृति कैसे परिवर्तित होगी?
उत्तर-
गोलीय पृष्ठ पर अपवर्तन का सूत्र

जहाँ n पृष्ठ के पदार्थ का वायु के सापेक्ष अपवर्तनांक है, u वस्तु की ध्रुव से दूरी है, v प्रतिबिम्ब की ध्रुव से दूरी है तथा R पृष्ठ की वक्रता-त्रिज्या है।
पतले लेन्स के लिए अपवर्तन का सूत्र- चित्र 9.25 में एक पतला लेन्स L वायु में रखा है। लेन्स के पदार्थ का वायु के सापेक्ष अपवर्तनांक n है तथा इसके पहले व दूसरे पृष्ठों की वक्रता-त्रिज्याएँ क्रमशः R1 व R2 हैं। माना लेन्स की मोटाई t है। एक बिन्दु-वस्तु O लेन्स की मुख्य अक्ष पर लेन्स के प्रथम पृष्ठ के ध्रुवे P1 से u दूरी पर रखी है। यह पृष्ठ O का प्रतिबिम्ब I’ बनाता है।
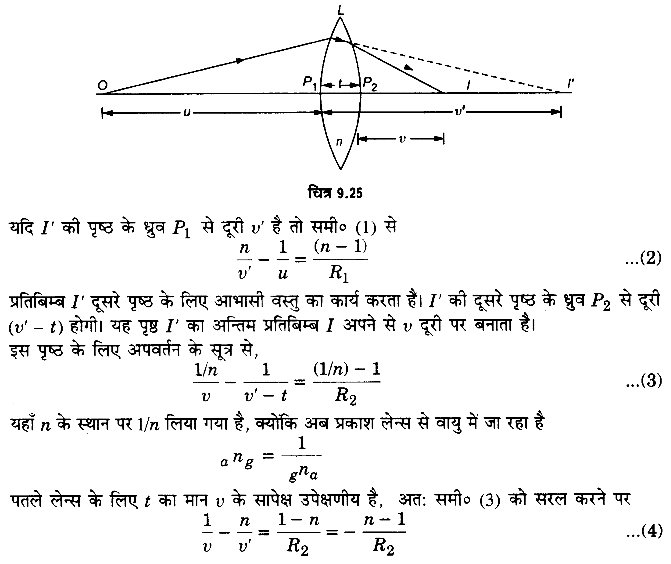

यही पतले लेन्स के अपवर्तन का सूत्र है। यदि काँच के लेन्स को ऐसे द्रव में डुबो दिया जाये जिसका अपवर्तनांक काँच के अपवर्तनांक से अधिक है, तो लेन्स की फोकस दूरी बढ़ जायेगी तथा इसके साथ-साथ फोकस दूरी का चिह्न भी उलट जायेगा अर्थात् लेन्स की प्रकृति उलट जायेगी।
प्रश्न 4.
एक 25 सेमी फोकस दूरी का उत्तल लेन्स 20 सेमी फोकस दूरी के अवतल लेन्स के सम्पर्क में रखा जाता है। इस संयोजन की क्षमता तथा प्रकृति ज्ञात कीजिए। संयोजन को 1.6 अपवर्तनांक वाले द्रव में रखे जाने पर फोकस दूरी तथा प्रकृति पर क्या प्रभाव पड़ेगा? लेन्सों के पदार्थ का अपवर्तनांक 1.5 है। (2014)

प्रश्न 5.
एक वस्तु किसी पर्दे से 60.0 सेमी की दूरी पर स्थित है। एक उत्तल लेन्स को इनके बीच दो भिन्न स्थानों पर रखने से पर्दे पर दो बार वास्तविक प्रतिबिम्ब बनते हैं। यदि प्रतिबिम्बों की लम्बाइयाँ 9.0 सेमी तथा 4.0 सेमी हों तो वस्तु की लम्बाई तथा लेन्स की फोकस दूरी ज्ञात कीजिए।
हल-
हम जानते हैं कि, विस्थापन विधि में

प्रश्न 6.
लेन्स द्वारा प्रकाश के अपवर्तन के लिए न्यूटन का सूत्र xx’ = ff’ स्थापित कीजिए। (2017)
उत्तर-
सूत्र की उपपत्ति- माना एक लेन्स का प्रकाशिक केन्द्र C है। F व F’ इसके फोकस बिन्दु तथा OCI मुख्य अक्ष है। O एक वस्तु है जिसका लेन्स द्वारा निर्मित प्रतिबिम्ब I है। इस प्रकार O तथा I संयुग्मी बिन्दु (conjugate points) हैं। O’ से चलने वाली आपतित किरण O’A जो मुख्य अक्ष के समान्तर है, अपवर्तन के पश्चात् लेन्स के फोकस F से होकर जाती है। दूसरी किरण O’B प्रथम फोकस बिन्दु से गुजरती हुई लेन्स से अपवर्तन के पश्चात् मुख्य अक्ष के समान्तर हो जाती है। दोनों निर्गत किरणें I’ पर मिलती हैं, जो O’ का वास्तविक प्रतिबिम्ब है। I’ से मुख्य अक्ष पर खींचा गया लम्ब II’ वस्तु OO’ का प्रतिबिम्ब है।
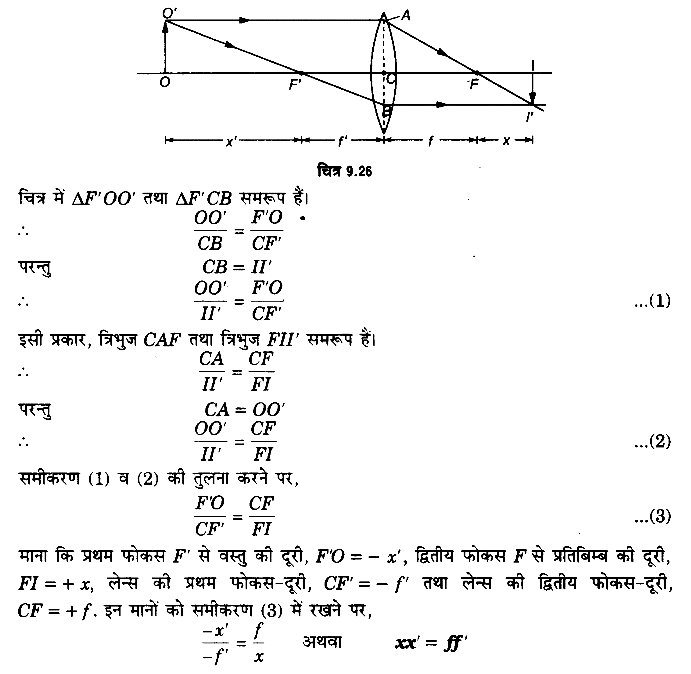
प्रश्न 7.
किसी उत्तल या अवतल गोलीय पृष्ठ पर आपतित प्रकाश के अपवर्तन के लिए सूत्र स्थापित कीजिए। n पदार्थ का वायु के सापेक्ष अपवर्तनांक तथा R गोलीय तल की त्रिज्या है। (2017)
उत्तर-
माना कि SPS’ एक उत्तल गोलीय पृष्ठ है जो निरपेक्ष अपवर्तनांक n1 के विरल माध्यम को निरपेक्ष अपवर्तनांक n2 के सघन माध्यम से पृथक् करता है। इस पृष्ठ का वक्रता केन्द्र C है तथा ध्रुव P है।
इसके मुख्य अक्ष PC पर (पीछे बढ़ाने पर) एक बिन्दु वस्तु O स्थित है। O से एक आपतित किरण OA, पृष्ठ पर बिन्दु A पर आपतित होती है, जहाँ CAN अभिलम्ब है। अपवर्तन के नियमानुसार, अपवर्तित किरण AB, अभिलम्ब की ओर मुड़ जाती है। दूसरी आपतित किरण OP पृष्ठ पर अभिलम्बवत् गिरती है, अतः बिना विचलित हुए सीधी चली जाती है। ये दोनों अपवर्तित किरणें पीछे बढ़ाये जाने पर बिन्दु I पर मिलती हैं। अतः वस्तु 0 का आभासी प्रतिबिम्ब बिन्दु I है।



प्रश्न 8.
प्रिज्म के पदार्थ के लिए अपवर्तनांक का सूत्र अल्पतम विचलन कोण तथा प्रिज्म कोण के पदों में निगमित कीजिए। (2009, 10, 11)
या
का निगमन कीजिए। यहाँ n प्रिज्म का अपवर्तनांक, A प्रिज्म का कोण तथा अल्पतम विचलन है। या किसी प्रिज्म के पदार्थ के अपवर्तनांक के लिये, प्रिज्म के कोण तथा न्यूनतम विचलन कोण के पदों में एक व्यंजक निकालिए। (2012)
उत्तर-
प्रिज्म के पदार्थ के अपवर्तनांक का सूत्र- चित्र 9.28 में, ABC प्रिज्म का मुख्य परिच्छेद है। प्रिज्म का अपवर्तन कोण A है। माना एक प्रकाश किरण RS, प्रिज्म के अपवर्तक पृष्ठ AB पर तिरछी आपतित होती है जो अभिलम्ब MSE की ओर झुक जाती है और ST दिशा में अपवर्तित हो जाती है। इस पृष्ठ पर आपतन कोण i1 वे अपवर्तन कोण r1 है। अपवर्तित किरण ST’ पृष्ठ AC पर अभिलम्ब NTE से दूर हटती हुई वायु में TU दिशा में निकल जाती है। पृष्ठ AC पर आपतन कोण, तथा निर्गत कोण i2 है। आपतित किरण RS तथा निर्गत किरण TU को पीछे की ओर बढ़ाने पर ये बिन्दु D पर मिलती हैं। आपतित किरण तथा निर्गत किरणों के बीच बना कोण δ विचलन कोण कहलाता है।
ΔDST में δ बहिष्कोण है, अत:



प्रश्न 9.
किसी प्रकाशिक माध्यम की ‘वर्ण-विक्षेपण क्षमता की परिभाषा दीजिए। किसी प्रिज्म के पदार्थ के लिए वर्ण-विक्षेपण क्षमता का सूत्र अपवर्तनांक के पदों में प्राप्त कीजिए। या किसी प्रकाशिक माध्यम की विक्षेपण क्षमता की परिभाषा लिखिए। (2016)
या
किसी प्रकाशिक माध्यम की वर्ण-विक्षेपण क्षमता का सूत्र लिखिए। क्या वर्ण-विक्षेपण क्षमता प्रिज्म के कोण पर निर्भर करती है? या किसी प्रिज्म की वर्ण-विक्षेपण क्षमता की परिभाषा दीजिए। (2010)
या
वर्ण-विक्षेपण क्षमता की परिभाषा दीजिए। (2013)
उत्तर-
जब श्वेत प्रकाश एक पतले प्रिज्म में से गुजरता है तो बैंगनी तथा लाल रंगों की निर्गत किरणों के बीच उत्पन्न कोणीय वर्ण-विक्षेपण तथा मध्यवर्ती (अर्थात् पीले रंग की) किरण के लिए विचलन कोण के अनुपात को प्रिज्म के पदार्थ की’वर्ण-विक्षेपण क्षमता’ (dispersive power) कहते हैं। इसे ω (ओमेगा) से प्रदर्शित करते हैं। अपवर्तनांक के पदों में वर्ण-विक्षेपण क्षमता सूत्र


प्रश्न 10.
उपयुक्त किरण आरेख द्वारा प्रिज्म के कोणीय वर्ण-विक्षेपण का सूत्र निकालिए। (2014)
उत्तर-
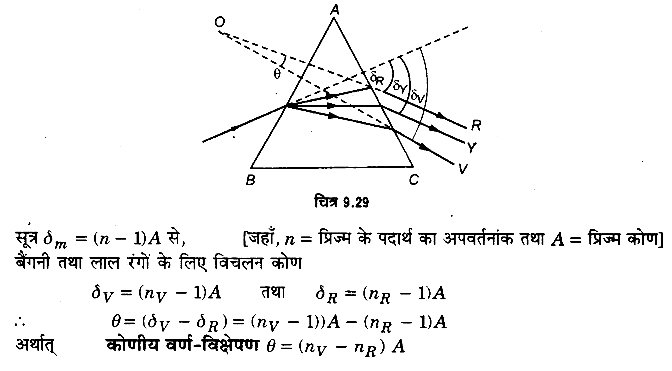
कोणीय वर्ण-विक्षेपण (परिक्षेपण) (Angular dispersion)- “दो रंगों की निर्गत किरणों के बीच का कोण उन रंगों के लिए कोणीय वर्ण-विक्षेपण (angular dispersion) कहलाता है।”
यदि δR व δv क्रमश: लाल तथा बैंगनी रंग की किरणों के लिए (अल्पतम) विचलन कोण हों तो उनके बीच कोणीय वर्ण-विक्षेपण θ = δV – δR
माना कि प्रिज्म के पदार्थ का अपवर्तनांक A है तथा nR व nV क्रमशः लाल व बैंगनी रंगों के लिए प्रिज्म के पदार्थ के अपवर्तनांक हैं। तब, पतले प्रिज्म से उत्पन्न विचलन के लिए
प्रश्न 11.
निकट दृष्टि दोष क्या है ? इसके क्या कारण हो सकते हैं? इसका निवारण किस प्रकार किया जाता है ? (2017)
या
निकट दृष्टि दोष क्या है? इसका निवारण किस प्रकार किया जाता है? (2014)
या
निकट दृष्टि दोष क्या है? (2016)
उत्तर-
निकट-दृष्टि दोष (Myopia or shortsightedness)- निकट दृष्टि दोष वाले व्यक्ति को पास की वस्तुएँ तो स्पष्ट दिखायी देती हैं; परन्तु अधिक दूर की वस्तुएँ स्पष्ट दिखायी नहीं देतीं अर्थात् नेत्र का दूर बिन्दु अनन्त पर न होकर कम दूरी पर आ जाता है। इस दोष के निम्नलिखित कारण हो सकते हैं।
- नेत्र लेन्स की वक्रता बढ़ जाए जिससे उसकी फोकस दूरी कम हो जाए।
- नेत्र लेन्स और रेटिना के बीच की दूरी बढ़ जाए अर्थात् नेत्र के गोले में लम्बापन आ जाए।
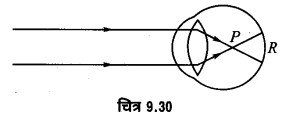
इस दोष के कारण दूर की वस्तु का प्रतिबिम्ब रेटिना पर न बेनकर उससे आगे बनने लगता है (चित्र 9.30) अर्थात् प्रतिबिम्ब रेटिना व नेत्र लेन्स के बीच P पर बन जाने से वस्तु स्पष्ट नहीं दिखती। ऐसे मनुष्य का दूर बिन्दु अनन्त पर न होकर आँख के काफी पास बनता है तथा निकट बिन्दु भी 25 सेमी से कम दूरी पर बनता है। दोष का निवारण-इस दोष में नेत्र का लेन्स अधिक अभिसारी (converging) हो जाता है; अत: इस दोष को दूर करने के लिए ऐसा लेन्स प्रयुक्त करना चाहिए जो नेत्र लेन्स को कम अभिसारी कर दे। इसलिए इस दोष को दूर करने के लिए उचित फोकस दूरी के अवतल लेन्स का प्रयोग करते हैं, ताकि इसे लेन्स तथा नेत्र लेन्स की संयुक्त फोकस दूरी बढ़कर इतनी हो जाए कि प्रतिबिम्ब रेटिना पर बनने लगे।
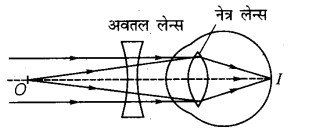
यदि निकट दृष्टि दोष वाले व्यक्ति का आँख के लिए दूर बिन्दु O हो, तो प्रयुक्त अवतल लेन्स अनन्त से आने वाली समान्तर किरणों का प्रतिबिम्ब O पर बनाएगा। यह प्रतिबिम्ब नेत्र लेन्स के लिए वस्तु का कार्य करेगा, जिससे अन्तिम प्रतिबिम्ब (I) रेटिना पर बनने लगेगा (चित्र 9.31)। स्पष्टतः प्रयुक्त लेन्स की फोकस दूरी नेत्र से नेत्र के दूर बिन्दु के बीच की दूरी के बराबर होगी।
प्रश्न 12.
दूर दृष्टि दोष क्या है ? इसके क्या कारण हो सकते हैं ? इसका निवारण किस प्रकार किया जाता है? (2017)
या
आँख का दूर दृष्टि दोष क्या है? इसका निवारण कैसे किया जाता है? (2014)
उत्तर-
दूर-दृष्टि दोष (Hypermetropia or longsightedness)- दूर दृष्टि दोष मनुष्य की आँख को वह दोष है, जिसमें मनुष्य दूर की वस्तुओं को तो स्पष्ट देख सकता है; परन्तु पास की वस्तुएँ स्पष्ट दिखायी नहीं पड़तीं। इसके निम्न दो कारण हो सकते हैं-
- नेत्र लेन्स की फोकस दूरी अधिक हो जाए अर्थात् लेन्स पतला हो जाए।
- आँख के गोले का व्यास कम हो जाए अर्थात् नेत्र लेन्स व रेटिना के बीच की दूरी कम हो जाए।
इन कारणों से पास की वस्तुओं के प्रतिबिम्ब रेटिना पर न बनकर उसके पीछे बनते हैं (चित्र 9.32)। दूसरे शब्दों में, नेत्र का निकट बिन्दु 25 सेमी से अधिक दूर हो जाता है।
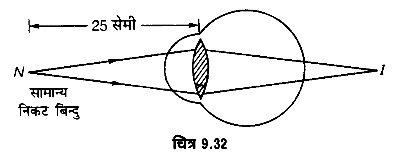
दोष का निवारण- चूँकि इस दोष में नेत्र लेन्स की फोकस दूरी बढ़ जाती है जिससे नेत्र लेन्स कम अभिसारी (converging) हो जाता है; अतः इस दोष को दूर करने के लिए एक-ऐसा लेन्स प्रयुक्त करना चाहिए जिससे वह अधिक अभिसारी हो जाए। इस दोष को दूर करने के लिए उपयुक्त फोकस दूरी का उत्तल लेन्स प्रयुक्त करते हैं ताकि इस लेन्स तथा नेत्र-लेन्स की संयुक्त फोकस दूरी इतनी हो जाये कि प्रतिबिम्ब रेटिना पर बनने लगे।
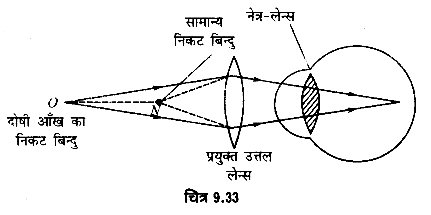
माना सामान्य आँख का निकट बिन्दु N तथा दूर दृष्टि से पीड़ित आँख का निकट बिन्दु O पर है। प्रयुक्त उत्तल लेन्स N पर रखी वस्तु का प्रतिबिम्ब O पर बनाने लगे, तब प्रतिबिम्ब O नेत्र लेन्स के लिए वस्तु का कार्य करेगा तथा नेत्र लेन्स अन्तिम प्रतिबिम्ब रेटिना पर बना देगा। इस प्रकार उचित फोकस दूरी का उत्तल लेन्स प्रयुक्त करने पर सामान्य निकट बिन्दु N पर रखी वस्तु भी आँख को स्पष्ट दिखाई देगी (चित्र 9.33)।
प्रश्न 13.
एक अपवर्तनी खगोलीय दूरदर्शी का किरण आरेख खींचिए जब अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है। इसकी आवर्धन क्षमता के लिए व्यंजक भी स्थापित कीजिए। (2016, 17)
या
खगोलीय दूरदर्शी का किरण आरेख बनाइए। जब अन्तिम प्रतिबिम्ब अनन्तता पर बन रहा है। दूरदर्शी में अभिदृश्यक लेन्स का द्वारक बड़े आकार का क्यों लिया जाता है? (2015)
या
खगोलीय दूरदर्शी द्वारा अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनने का किरण आरेख बनाइए। (2017)
उत्तर-
खगोलीय दूरदर्शी (Astronomical Telescope)- खगोलीय दूरदर्शी एक ऐसा प्रकाशिक यन्त्र है जिसके द्वारा उना दूर स्थित वस्तु का प्रतिबिम्ब का आँख पर बड़ा दर्शन कोण बनाता है जिससे कि वह वस्तु आँख को बड़ी दिखायी पड़ती है।
रचना- इसमें धातु की एक लम्बी बेलनाकार नली होती है जिसके एक सिरे पर बड़ी फोकस-दूरी तथा बड़े द्वारक का अवर्णक उत्तल लेन्स लगा होता है, जिसे ‘अभिदृश्यक लेन्स’ कहते हैं। नली के दूसरे सिरे पर एक अन्य छोटी नली फिट होती है जो दन्तुर दण्ड-चक्र (रैक-पिनयन) व्यवस्था द्वारा बड़ी नली में आगे-पीछे खिसकाई जा सकती है। छोटी नली के बाहरी सिरे पर एक छोटी फोकस-दूरी तथा छोटे द्वारकं को अवर्णक उत्तल लेन्स लगा रहता है जिसे अभिनेत्र लेन्स अथवा नेत्रिका कहते हैं। नेत्रिका के फोकस पर क्रॉस-तार लगे रहते हैं।
समायोजन- सबसे पहले नेत्रिको को छोटी नली में आगे-पीछे खिसकाकर क्रॉस-तार पर फोकस करे लेते हैं। फिर जिस वस्तु को देखना हो उसकी ओर अभिदृश्यक लेन्स को दिष्ट कर देते हैं। दन्तुर-दण्ड-चक्र व्यवस्था द्वारा छोटी नली को लम्बी नली में आगे-पीछे खिसकाकर अभिदृश्यक लेन्स की क्रॉस-तार से दूरी इस प्रकार समायोजित करते हैं कि वस्तु के प्रतिबिम्ब और क्रॉस-तार में लम्बन न रहे। इस स्थिति में वस्तु का स्पष्ट प्रतिबिम्ब दिखाई देगा। यह प्रतिबिम्ब लेन्सों द्वारा प्रकाश के अपवर्तन से बनता है। अतः यह दूरदर्शी अपवर्तक’ दूरदर्शी है।
प्रतिबिम्ब का बनना- चित्र 9.34 में दूरदर्शी का अभिदृश्यक लेन्स O तथा नेत्रिका E। दिखाये गये हैं। AB एक दूर-स्थित वस्तु है। जिसका A सिरा दूरदर्शी की अक्ष पर है। लेन्स -14 0 के द्वारा AB का वास्तविक, उल्टा व छोटा प्रतिबिम्ब A’B’, लेन्स के द्वितीय फोकस F0 पर बनता है। यह प्रतिबिम्ब नेत्रिका E के प्रथम फोकस Fe के भीतर है तथा नेत्रिका के लिए वस्तु का कार्य करता है। अतः नेत्रिका, A’B’ का आभासी, सीधा तथा बड़ा प्रतिबिम्ब A”B” बनाती है। B” की स्थिति ज्ञात करने के लिए, B’ से दो विछिन्न किरणें (………) ली गई हैं। एक किरण जो E के प्रकाशिक-केन्द्र में से जाती है, सीधी चली जाती है तथा दूसरी किरण जो मुख्य अक्ष से समान्तर ली गई है, E के दूसरे फोकस F, से होकर जाती है। ये किरणें पीछे बढ़ाने पर बिन्दु B” पर मिलती हैं।

आवर्धन-क्षमता- दूरदर्शी की आवर्धन-क्षमता (कोणीय आवर्धन)


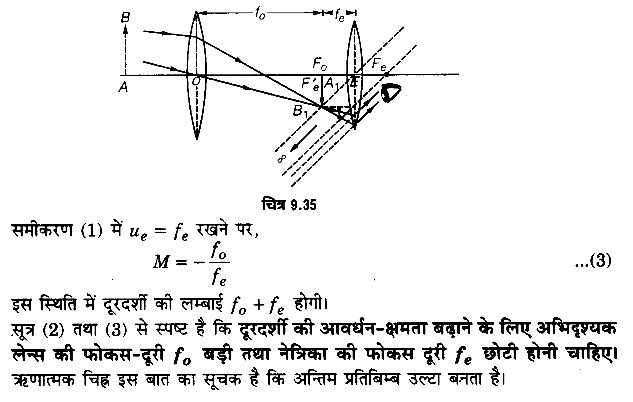
प्रश्न 14.
किसी परावर्ती दूरदर्शी का किरण आरेख खींचकर उसमें प्रतिबिम्ब का बनना प्रदर्शित कीजिए। (2009, 16, 17)
या
परावर्ती दूरदर्शी का किरण आरेख खींचिए तथा इसकी आवर्धन-क्षमता का सूत्र लिखिए जब प्रतिबिम्ब (i) अनन्त पर बन रहा हो। (ii) स्पष्ट दृष्टि की न्यूनतम दूरी पर बन रहा हो। (2011)
या
परावर्ती दूरदर्शी में प्रतिबिम्ब का बनना किरण-आरेख द्वारा समझाइए। अपवर्ती दूरदर्शी की तुलना में परावर्ती दूरदर्शी का क्या लाभ है? (2009, 10, 11)
या
परावर्ती दूरदर्शी का किरण आरेख खींचिए तथा इसकी कार्यविधि समझाइए। किसी दूरदर्शी की विभेदन क्षमता कैसे बढ़ाई जा सकती है? (2012)
या
परावर्ती दूरदर्शी की विशेषताओं का उल्लेख कीजिए। (2017)
या
किसी परावर्ती दूरदर्शी से प्रतिबिम्ब का बनना किरण आरेख द्वारा समझाइए। अपवर्ती दूरदर्शी की अपेक्षा परावर्ती दूरदर्शी क्यों अच्छी होती है? (2017)
उत्तर-
परावर्ती दूरदर्शी की रचना एवं उसके द्वारा प्रतिबिम्ब बनने की किरण आरेख चित्र 9.36 में प्रदर्शित किया गया है। इसमें अभिदृश्यक एक बड़े आकार तथा बड़ी फोकस दूरी का । अवतल दर्पण M1 होता है जो एक चौड़ी नली के एक सिरे पर। लगा रहता है। नली का खुला सिरा दूर स्थित वस्तु की ओर करके रखा जाता है। नली में अवतल दर्पण के फोकस से कुछ पहले एक समतल दर्पण M2 मुख्य अक्ष से 45° कोण पर झुका हुआ रखा जाता है। दूरदर्शी की इस चौड़ी नली के बगल में एक पतली नली लगी होती है जिसमें कम फोकस दूरी तथा छोटी द्वारक का एक अवर्णक उत्तल लेन्स E लगा रहता है, जिसे नेत्रिका कहते हैं।
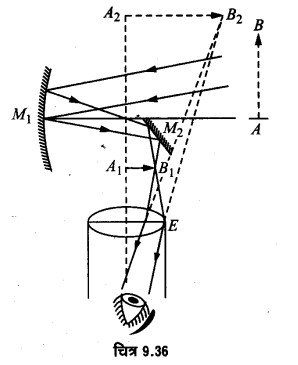
अवतल दर्पण M1 दूर स्थित वस्तु AB से आने वाली समान्तर किरणों को अपने फोकस पर केन्द्रित करता है। परन्तु ये किरणें फोकस पर केन्द्रित होने से पूर्व फोकस से पहले 45° कोण पर झुके समतल दर्पण M2 पर आपतित होती हैं। समतल दर्पण इन किरणों को परावर्तित करके AB का छोटा, वास्तविक, उल्टा प्रतिबिम्बे A1B1 बनाता है। नेत्रिका E द्वारा A1B1 का वास्तविक, सीधा तथा बड़ा प्रतिबिम्ब A2B2 स्पष्ट दृष्टि की न्यूनतम दूरी तथा अनन्त के बीच में बन जाता है। जब प्रतिबिम्ब A1B1 नेत्रिका के फोकस पर बन जाता है, तो अन्तिम प्रतिबिम्ब A2B2 अनन्त पर बनेगा।
आवर्धन क्षमता सूत्र

अपवर्ती दूरदर्शी की तुलना में परावर्ती दूरदर्शी के लाभ- अपवर्ती दूरदर्शी की तुलना में परावर्ती दूरदर्शी के निम्नलिखित लाभ हैं-
- परावर्ती दूरदर्शक में प्रकाश अवशोषण बहुत कम होता है; अत: इससे निर्मित प्रतिबिम्ब, समान द्वारक के अपवर्ती दूरदर्शक की अपेक्षा अधिक चमकीला होता है।
- परावर्ती दूरदर्शक से बना अन्तिम प्रतिबिम्ब वर्ण-विपथन दोष से पूर्णतः मुक्त होता है।
- इसमें परवलयाकार दर्पणों के प्रयोग से गोलीय विपथन दोष भी स्वतः दूर हो जाता है जिससे प्रतिबिम्ब टेढ़े दिखायी नहीं देते।
- दूरदर्शी से दूर-स्थित वस्तु को चमकीला प्रतिबिम्ब बनाने के लिए उसके अभिदृश्यक का द्वारक बड़ा (large) होना आवश्यक है। तकनीकी दृष्टि से बड़े द्वारक के लेन्स को ढालने (casting) की क्रिया में उसके पदार्थ में विकृति आ जाती है, क्योंकि बड़े आकार के गर्म काँच को एकसमान (uniformly) ठण्डा करना कठिन होता है। फलस्वरूप इनसे निर्मित प्रतिबिम्ब भी विकृत हो जाते हैं। चूँकि दर्पण से परावर्तन द्वारा प्रतिबिम्ब निर्मित होते हैं, प्रकाश की किरण केवल दर्पण के पृष्ठ को स्पर्श करती है, उसके पदार्थ में होकर नहीं गुजरती है। अत: दर्पण के पदार्थ में कोई विकृति होने पर उसका प्रतिबिम्ब पर प्रभाव नहीं पड़ता।
- दूरदर्शी की विभेदन क्षमता = d/1.22 λ अतः अभिदृश्यक का द्वारक d बढ़ाकर दूरदर्शी की विभेदन क्षमता बढ़ायी जा सकती है।
- परावर्ती दूरदर्शी में परवलयाकार दर्पण के उपयोग से प्रतिबिम्ब में गोलीय विपथन के दोष को दूर किया जा सकता है।
प्रश्न 15.
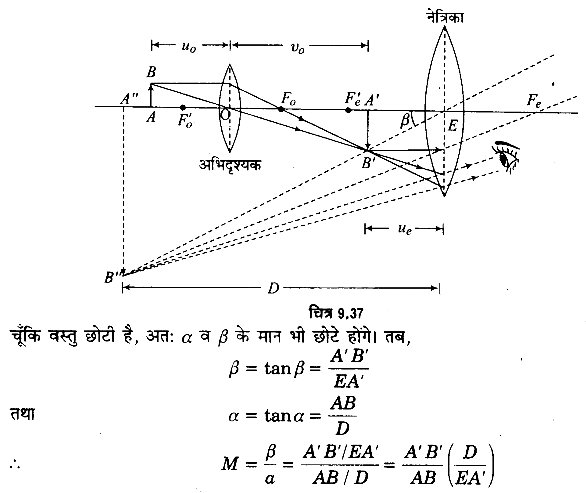
संयुक्त सूक्ष्मदर्शी का नामांकित किरण आरेख बनाइए तथा इसकी आवर्धन क्षमता का सूत्र ज्ञात कीजिए, जब अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है। (2016)
उत्तर-
आवर्धन-क्षमता- माना कि अन्तिम प्रतिबिम्ब A” B” नेत्रिका E पर β कोण बनाता है। आँख नेत्रिका के समीप है, अतः A” B” द्वारा आँख पर बनने वाले कोण को भी β मान सकते हैं। माना कि यदि वस्तु AB आँख से स्पष्ट दृष्टि की न्यूनतम दूरी D पर हो, तो वह आँख पर α कोण बनाती है। अब, सूक्ष्मदर्शी की आवर्धन-क्षमता


We hope the UP Board Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments (किरण प्रकाशिकी एवं प्रकाशिक यंत्र) help you.