UP Board Solutions for Class 9 Maths Chapter 15 Probability (प्रायिकता)

UP Board Solutions for Class 9 Maths Chapter 15 Probability (प्रायिकता)

प्रश्नावली 15.1

प्रश्न 1.
एक क्रिकेट मैच में, एक महिला बल्लेबाज खेली गई 30 गेंदों में 6 बार चौका मारती है। चौका न मारे जाने की प्रायिकता ज्ञात कीजिए।
हल :
महिला बल्लेबाज द्वारा 30 गेंदें खेली गईं।
यहाँ चौका मारे जाने की कुल सम्भावनाएँ 30 हैं। चौका लगने के अनुकूल परिणाम 6 हैं।

अतः महिला बल्लेबाज द्वारा चौका न मारे जाने की प्रायिकता है।

प्रश्न 2.
2 बच्चों वाले 1500 परिवारों का यदृच्छया चयन किया गया है और निम्नलिखित आँकड़े लिख लिए गए हैं :

यदृच्छयो चुने गए उस परिवार की प्रायिकता ज्ञात कीजिए, जिसमें
(i) दो लड़कियाँ हों,
(ii) एक लड़की हो,
(iii) कोई लड़की न हो।
साथ ही, यह भी जाँच कीजिए कि इन प्रायिकताओं का योगफल 1 है या नहीं।
हल :
यहाँ पर कुल परिवार = 1500
(i) 2 लड़कियों वाले परिवारों के अनुकूल परिणाम 475 हैं।

प्रश्न 3.
नवीं कक्षा के 40 विद्यार्थियों से उनके जन्म का महीना बताने के लिए कहा गया। इस प्रकार प्राप्त आँकड़ों से निम्नलिखित आलेख बनाया गया।

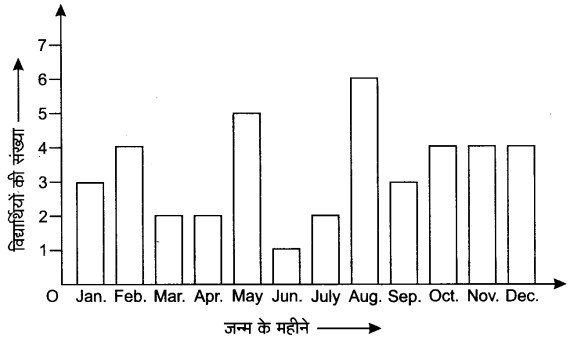
कक्षा के किसी एक विद्यार्थी का जन्म अगस्त में होने की प्रायिकता ज्ञात कीजिए।
हल :
दिए गए आलेख को देखने से स्पष्ट है कि अगस्त में जन्म लेने वाले विद्यार्थियों की संख्या 06 है।
यहाँ यदृच्छया चुने गए किसी विद्यार्थी के जन्म का माह अगस्त होना एक घटना है जिसके अनुकूल परिणाम 06 हैं और कुल सम्भावित परिणाम अर्थात कक्षा में विद्यार्थियों की संख्या 40 हैं।

प्रश्न 4.
तीन सिक्कों को एक साथ 200 बार उछाला गया है तथा इनमें विभिन्न परिणामों की बारम्बारताएँ ये हैं :

यदि तीनों सिक्कों को पुनः एक साथ उछाला जाए, तो दो चित के आने की प्रायिकता ज्ञात कीजिए।
हल :
यहाँ कुल उछाल = 200
तथा 2 चित आने की विधियाँ = 72

प्रश्न 5.
एक कम्पनी ने यदृच्छया 2400 परिवार चुनकर एक घर की आय स्तर और वाहनों की संख्या के बीच सम्बन्ध स्थापित करने के लिए उनका सर्वेक्षण किया। एकत्रित किए गए आँकड़े नीचे सारणी में दिए गए हैं :

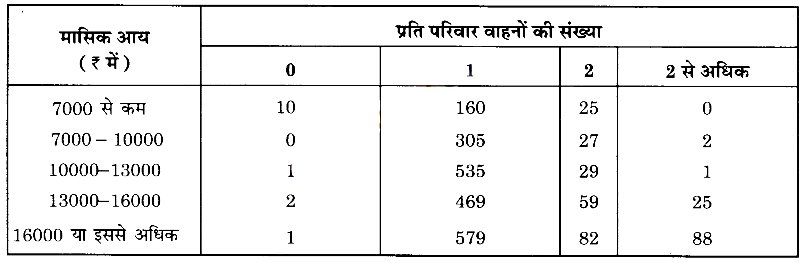
मान लीजिए एक परिवार चुना गया है। प्रायिकता ज्ञात कीजिए कि चुने गए परिवार
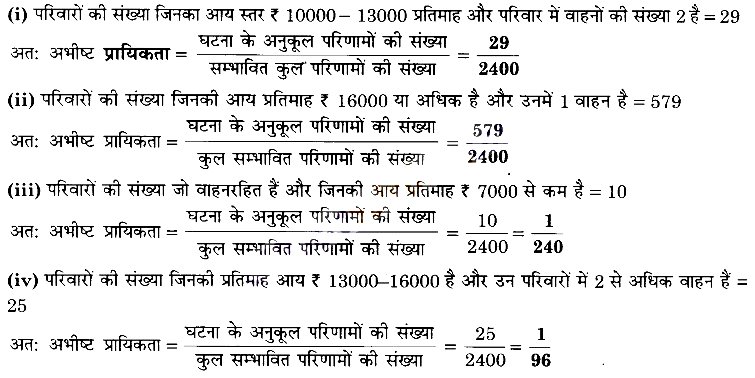
(i) की आय ₹ 10000-13000 प्रतिमाह है और उसके पास ठीक-ठीक दो वाहन हैं।
(ii) की आय प्रतिमाह ₹ 16000 या इससे अधिक है और उसके पास ठीक 1 वाहन है।
(iii) की आय ₹ 7000 प्रतिमाह से कम है और उसके पास कोई वाहन नहीं है।
(iv) की आय ₹ 13000-16000 प्रतिमाह है और उसके पास 2 से अधिक वाहन हैं।
(v) जिसके पास 1 से अधिक वाहन नहीं है।
हल :
एक कम्पनी द्वारा चुने गए कुल परिवारों की संख्या = 2400

प्रश्न 6.
निम्न सारणी में विद्यार्थियों के प्राप्तांक और उनकी संख्या दी गई है :

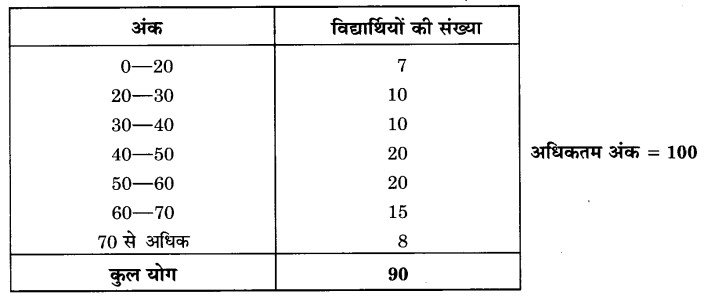
(i) गणित की परीक्षा में एक विद्यार्थी द्वारा 20% से कम अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
(ii) एक विद्यार्थी द्वारा 60 या इससे अधिक अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
हल :
(i) परीक्षण हेतु चयनित विद्यार्थी = 90
20% से कम अंक प्राप्त करने वाले विद्यार्थियों की संख्या = 7

प्रश्न 7.
सांख्यिकी के बारे में विद्यार्थियों का मत जानने के लिए 200 विद्यार्थियों का सर्वेक्षण किया गया। प्राप्त आँकड़ों को नीचे दी गई सारणी में लिख लिया गया है :

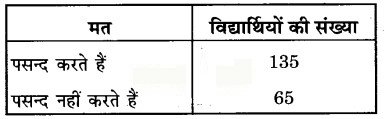
प्रायिकता ज्ञात कीजिए कि यदृच्छया चुना गया विद्यार्थी
(i) सांख्यिकी पसन्द करता है।
(ii) सांख्यिकी पसन्द नहीं करता है।
हल :
सांख्यिकी के बारे में सर्वेक्षण के लिए चुने गए विद्यार्थियों की संख्या = 200
मत जाना गया कि 135 विद्यार्थी सांख्यिकी पसन्द करते हैं और 65 विद्यार्थी इसे पसन्द नहीं करते।
एक विद्यार्थी यदृच्छया चुना जाता है।
(i) तब सांख्यिकी पसन्द करने के अनुकूल प्रेक्षण = 135
और सांख्यिकी पसन्द करने के कुल सम्भावित प्रेक्षण = 200
अत: चयनित छात्र के सांख्यिकी पसन्द करने की प्रायिकता P(E)

प्रश्न 8.
40 इंजीनियरों की उनके आवास से कार्यस्थल की दूरियाँ (किमी में) निम्नलिखित हैं :

इसकी आनुभविक प्रायिकता क्या होगी कि इंजीनियर
(i) अपने कार्यस्थल से 7 किमी से कम दूरी पर रहते हैं?
(ii) अपने कार्यस्थल से 7 किमी या इससे अधिक दूरी पर रहते हैं?
(iii) अपने कार्यस्थल से 3 किमी या इससे कम दूरी पर रहते हैं?
हल :
इंजीनियरों की कुल संख्या = 40
कार्यस्थल से 7 किमी से कम दूरी पर आवास वाले इंजीनियरों की संख्या = 9
कार्यस्थल से 7 किमी या अधिक दूरी पर आवास वाले इंजीनियरों की संख्या = 40 – 9 = 31

प्रश्न 9.
क्रियाकलाप : अपने विद्यालय के गेट के सामने से एक समय-अन्तराल में गुजरने वाले दो पहिया, तीन पहिया और चार पहिया वाहनों की बारम्बारता लिख लीजिए। आप द्वारा देखे गए वाहनों में से किसी एक वाहन का दो पहिया वाहन होने की प्रायिकता ज्ञात कीजिए।
हल :
निम्न प्रारूप पर सूचना एकत्र कीजिए :

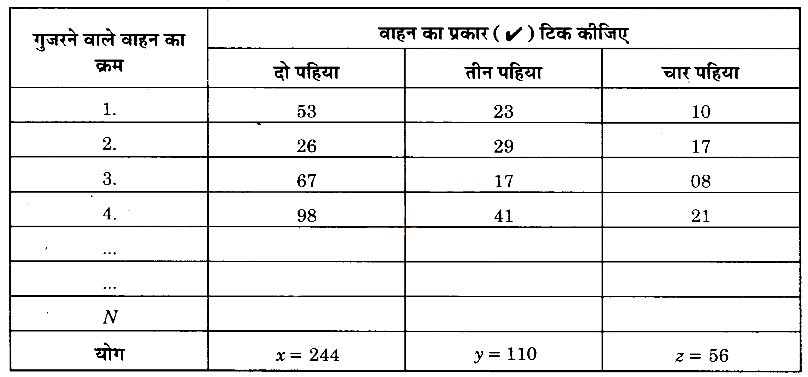
सारणी से, कुल सम्भावित परिणाम (N) = x + y + z = 244 + 110 + 56 = 410
तथा दो पहिया वाहनों की संख्या (x) = 244
तब, गुजरने वाले वाहन के दो पहिया वाहन होने की प्रायिकता = = = 0.59
नोट : विद्यार्थी अपनी सुविधा से आँकड़े ले सकते हैं।

प्रश्न 10.
क्रियाकलाप : आप अपनी कक्षा के विद्यार्थियों से एक 3 अंक वाली संख्या लिखने को कहिए। आप कक्षा से एक विद्यार्थी को यदृच्छया चुन लीजिए। इस बात की प्रायिकता क्या होगी कि उसके द्वारा लिखी गई संख्या 3 से भाज्य है? याद रखिए कि कोई संख्या 3 से भाज्य होती है, यदि उसके अंकों का योग 3 से भाज्य हो।
हल :
तीन अंकों वाली संख्याएँ 100 से प्रारम्भ होकर 999 तक हैं। 100 से 999 तक के बीच कुल सम्भावित संख्याएँ 900 हैं। इन नौ सौ संख्याओं में प्रत्येक तीसरी संख्या 3 से विभाज्य होगी।
इस प्रकार 3 अंकों वाली कुल संख्याएँ = 900
3 से विभाज्य 3 अंकों वाली कुल संख्याएँ = = 300

प्रश्न 11.
आटे की उन ग्यारह थैलियों में, जिन पर 5 किग्रा अंकित है, वास्तव में आटे के निम्नलिखित भार (किग्रा में ) हैं :
4.97, 5.06, 5.08 5.03, 5.00, 5.06, 5.08 4.98, 5.04 5.07, 5.00 यदृच्छया चुनी गई एक थैली में 5 किग्रा से अधिक आटा होने की प्रायिकता क्या होगी?
हल :
आटे की 11 थैलियों के भार (किग्रा में) :
4.97, 4.98 5.00, 5.00, 5.03, 5.04, 5.06, 5.06, 5.07, 5.08, 5.08,
स्पष्ट है कि 7 थैलियों का आटा 5 किग्रा से अधिक है।
यहाँ यदृच्छया थैली का चुनना एक घटना है जिसकी कुल सम्भावित संख्या 11 है और थैली के 5 किग्रा से अधिक होने की सम्भावनाएँ 7 हैं।

प्रश्न 12.
एक नगर में वायु में सल्फर डाइऑक्साइड का सान्द्रण भाग प्रति मिलियन [parts per million (ppm)] में ज्ञात करने के लिए एक अध्ययन किया गया। 30 दिनों के प्राप्त किए गए आँकड़े ये हैं

किसी एक दिन वर्ग अन्तराल (0.12 – 0.16) में सल्फर डाइऑक्साइड के सान्द्रण होने की प्रायिकता ज्ञात कीजिए।
हल :
निम्नतम सान्द्रण = 0.01
उच्चतम सान्द्रण = 0.22
आँकड़ों का परिसर = 0.22 – 0.01 = 0.21
वर्ग की आमाप = 0.16 – 0.12 = 0.04
वर्गों की संख्या = + 1 = 5 + 1 = 6

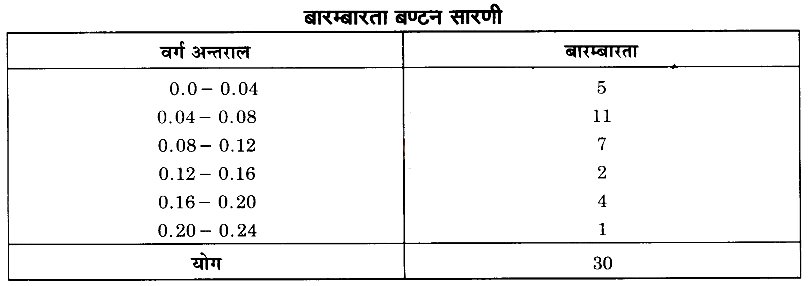
प्रश्न 13.
आठवीं कक्षा के 30 विद्यार्थियों के रक्त समूह ये हैं :
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
कक्षा से यदृच्छया चुने गए एक विद्यार्थी का रक्त समूह AB होने की प्रायिकता ज्ञात कीजिए।

We hope the UP Board Solutions for Class 9 Maths Chapter 15 Probability (प्रायिकता) help you.